6.1 光电效应及其解释 课件 (共18张PPT) 高二下学期物理鲁科版(2019)选择性必修第三册
文档属性
| 名称 | 6.1 光电效应及其解释 课件 (共18张PPT) 高二下学期物理鲁科版(2019)选择性必修第三册 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-04-27 21:22:01 | ||
图片预览




文档简介
(共18张PPT)
第六章 波粒二象性
鲁科版2019选择性必修三
第1节光电效应及其解释
思考:光究竟是什么?
新课引入
★牛顿的微粒说
★惠更斯的波动说
★麦克斯韦的电磁说
用弧光灯照射擦得很亮的锌板,(注意用导线与不带电的验电器相连),使验电器张角增大到约为 30度时,再用与丝绸摩擦过的玻璃棒去靠近锌板,则验电器的指针张角会变大。
表明锌板在射线照射下失去电子而带正电
一、光电效应
二、二、光电效应的实验规律
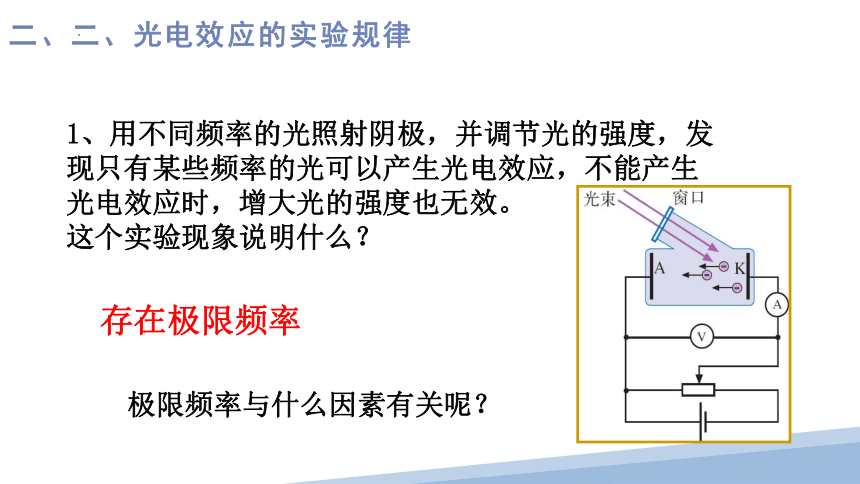
1、用不同频率的光照射阴极,并调节光的强度,发现只有某些频率的光可以产生光电效应,不能产生光电效应时,增大光的强度也无效。
这个实验现象说明什么?
存在极限频率
极限频率与什么因素有关呢?
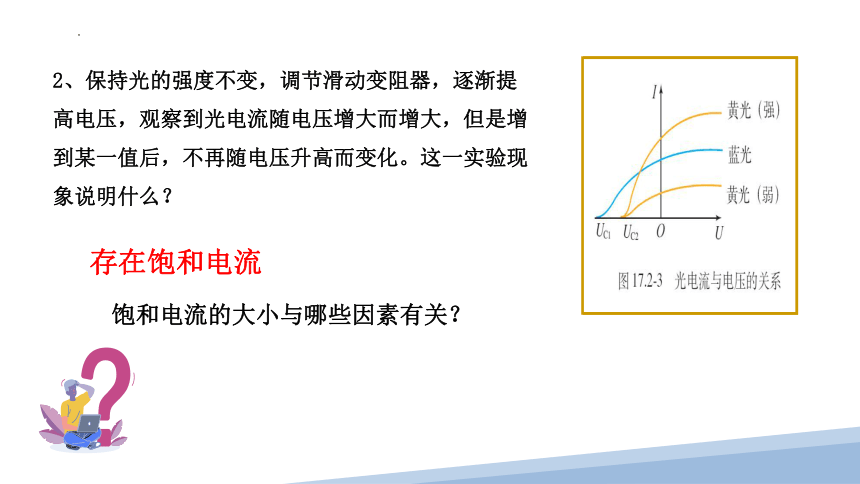
2、保持光的强度不变,调节滑动变阻器,逐渐提高电压,观察到光电流随电压增大而增大,但是增到某一值后,不再随电压升高而变化。这一实验现象说明什么?
存在饱和电流
饱和电流的大小与哪些因素有关?
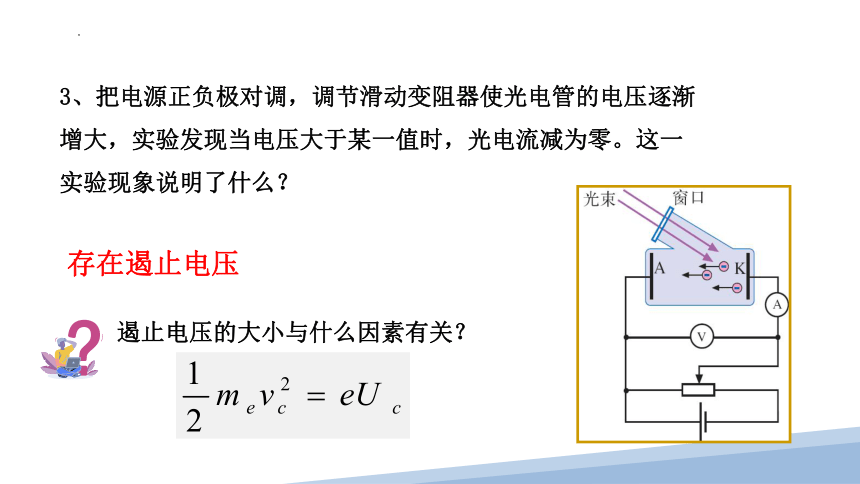
3、把电源正负极对调,调节滑动变阻器使光电管的电压逐渐增大,实验发现当电压大于某一值时,光电流减为零。这一实验现象说明了什么?
存在遏止电压
遏止电压的大小与什么因素有关?
知识梳理
1.存在极限频率(截止频率)
任何一种金属,都存在极限频率ν0,只有当入射光频率ν>ν0时,才能发生光电效应.
3.光电效应的发生时间:几乎是瞬时发生的。
2.存在饱和电流
当入射光频率ν>ν0时,光电流随入射光强度的增大而增大。
4.存在遏制电压
光电子的最大初动能Ekm与入射光强度无关,只随入射光频率的增大而增大。
爱因斯坦的光子说和光电效应方程
1.光子说(爱因斯坦于1905年提出)
光不仅在发射和吸收时能量是一份一份的,而且光本身就是由一个个不可分割的能量子组成,光的这些能量子叫做光子。即:E=hν ,ν 表示光的频率,h 叫普朗克常量,
h=6.63×10-34焦耳·秒
光子能量
逸出功
最大初动能
光电效应方程
三、对光电效应的解释
为什么存在极限频率?
为什么存在饱和电流?
为什么存在遏止电压?
为什么可以瞬间完成?
例1利用光电管研究光电效应实验如图所示,用频率为ν的可见光照射阴极K,电流表中有电流通过,则( )
A.用紫外线照射,电流表不一定有电流通过
C.用频率为ν的可见光照射K,当滑动变
阻器的滑动触头移到A端时,电流表中一定无电流通过
D.用频率为ν的可见光照射K,当滑动变阻器的滑动
触头向B端滑动时,电流表示数可能不变
典型例题
例2(2016新课标I)现用某一光电管进行光电效应实验,当用某一频率的光入射时,有光电流产生。下列说法正确的是__________。
A.保持入射光的频率不变,入射光的光强变大,饱和光电流变大
B.入射光的频率变高,饱和光电流变大
C.入射光的频率变高,光电子的最大初动能变大
D.保持入射光的光强不变,不断减小入射光的频率,始终有光电流产生
E.遏止电压的大小与入射光的频率有关,与入射光的光强无关
例3如图所示,当电键K断开时,用光子能量为2.5 eV的一束光照射阴极P,发现电流表读数不为零.合上电键,调节滑动变阻器,发现当电压表读数小于0.60 V时,电流表读数仍不为零.当电压表读数大于或等于0.60 V时,电流表读数为零.由此可知阴极材料的逸出功为( )
A.1.9 eV B.0.6 eV
C.2.5 eV D.3.1 eV
例4.光电效应实验装置示意如图所示.用频率为ν的普通光源照射阴极K,没有发生光电效应.换用同样频率ν的强激光照射阴极K,则发生了光电效应;此时,若加上反向电压U,即将阴极K接电源正极,阳极A接电源负极,在K、A之间就形成了使光电子减速的电场.逐渐增大U,光电流会逐渐减小;当光电流恰好减小到零时,所加反向电压U可能是(其中W为逸出功,h为普朗克常量,e为电子电荷量)( )
康普顿效应
光的色散现象很常见。按照波动理论,色散光和入射光的频率应该是一致的。但是康普顿研究X射线通过石墨等物质时,散射射线中有其他波长的X射线,这个现象成为康普顿效应。
如何解释这一现象呢?
光的波粒二象性
光到底是什么?
哪些现象说明光具有波动性?
哪些现象说明光具有粒子性?
什么时候呈现波动性?什么时候呈现粒子性?
例5.关于光的本性,下列说法中正确的是( )
A.关于光的本性,牛顿提出“微粒说”.惠更斯提出“波动说”,爱因斯坦提出“光子说”,它们都说明了光的本性
B.光具有波粒二象性是指:既可以把光看成宏观概念上的波,也可以看成微观概念上的粒子
C.光的干涉、衍射现象说明光具有波动性
D.光电效应说明光具有粒子性
例6.科学研究证明,光子有能量也有动量,当光子与电子碰撞时,光子的一些能量转移给了电子.假设光子与电子碰撞前的波长为λ,碰撞后的波长为λ′,则碰撞过程中( )
A.能量守恒,动量守恒,且λ=λ′
B.能量不守恒,动量不守恒,且λ=λ′
C.能量守恒,动量守恒,且λ<λ′
D.能量守恒,动量守恒,且λ>λ′
第六章 波粒二象性
鲁科版2019选择性必修三
第1节光电效应及其解释
思考:光究竟是什么?
新课引入
★牛顿的微粒说
★惠更斯的波动说
★麦克斯韦的电磁说
用弧光灯照射擦得很亮的锌板,(注意用导线与不带电的验电器相连),使验电器张角增大到约为 30度时,再用与丝绸摩擦过的玻璃棒去靠近锌板,则验电器的指针张角会变大。
表明锌板在射线照射下失去电子而带正电
一、光电效应
二、二、光电效应的实验规律
1、用不同频率的光照射阴极,并调节光的强度,发现只有某些频率的光可以产生光电效应,不能产生光电效应时,增大光的强度也无效。
这个实验现象说明什么?
存在极限频率
极限频率与什么因素有关呢?
2、保持光的强度不变,调节滑动变阻器,逐渐提高电压,观察到光电流随电压增大而增大,但是增到某一值后,不再随电压升高而变化。这一实验现象说明什么?
存在饱和电流
饱和电流的大小与哪些因素有关?
3、把电源正负极对调,调节滑动变阻器使光电管的电压逐渐增大,实验发现当电压大于某一值时,光电流减为零。这一实验现象说明了什么?
存在遏止电压
遏止电压的大小与什么因素有关?
知识梳理
1.存在极限频率(截止频率)
任何一种金属,都存在极限频率ν0,只有当入射光频率ν>ν0时,才能发生光电效应.
3.光电效应的发生时间:几乎是瞬时发生的。
2.存在饱和电流
当入射光频率ν>ν0时,光电流随入射光强度的增大而增大。
4.存在遏制电压
光电子的最大初动能Ekm与入射光强度无关,只随入射光频率的增大而增大。
爱因斯坦的光子说和光电效应方程
1.光子说(爱因斯坦于1905年提出)
光不仅在发射和吸收时能量是一份一份的,而且光本身就是由一个个不可分割的能量子组成,光的这些能量子叫做光子。即:E=hν ,ν 表示光的频率,h 叫普朗克常量,
h=6.63×10-34焦耳·秒
光子能量
逸出功
最大初动能
光电效应方程
三、对光电效应的解释
为什么存在极限频率?
为什么存在饱和电流?
为什么存在遏止电压?
为什么可以瞬间完成?
例1利用光电管研究光电效应实验如图所示,用频率为ν的可见光照射阴极K,电流表中有电流通过,则( )
A.用紫外线照射,电流表不一定有电流通过
C.用频率为ν的可见光照射K,当滑动变
阻器的滑动触头移到A端时,电流表中一定无电流通过
D.用频率为ν的可见光照射K,当滑动变阻器的滑动
触头向B端滑动时,电流表示数可能不变
典型例题
例2(2016新课标I)现用某一光电管进行光电效应实验,当用某一频率的光入射时,有光电流产生。下列说法正确的是__________。
A.保持入射光的频率不变,入射光的光强变大,饱和光电流变大
B.入射光的频率变高,饱和光电流变大
C.入射光的频率变高,光电子的最大初动能变大
D.保持入射光的光强不变,不断减小入射光的频率,始终有光电流产生
E.遏止电压的大小与入射光的频率有关,与入射光的光强无关
例3如图所示,当电键K断开时,用光子能量为2.5 eV的一束光照射阴极P,发现电流表读数不为零.合上电键,调节滑动变阻器,发现当电压表读数小于0.60 V时,电流表读数仍不为零.当电压表读数大于或等于0.60 V时,电流表读数为零.由此可知阴极材料的逸出功为( )
A.1.9 eV B.0.6 eV
C.2.5 eV D.3.1 eV
例4.光电效应实验装置示意如图所示.用频率为ν的普通光源照射阴极K,没有发生光电效应.换用同样频率ν的强激光照射阴极K,则发生了光电效应;此时,若加上反向电压U,即将阴极K接电源正极,阳极A接电源负极,在K、A之间就形成了使光电子减速的电场.逐渐增大U,光电流会逐渐减小;当光电流恰好减小到零时,所加反向电压U可能是(其中W为逸出功,h为普朗克常量,e为电子电荷量)( )
康普顿效应
光的色散现象很常见。按照波动理论,色散光和入射光的频率应该是一致的。但是康普顿研究X射线通过石墨等物质时,散射射线中有其他波长的X射线,这个现象成为康普顿效应。
如何解释这一现象呢?
光的波粒二象性
光到底是什么?
哪些现象说明光具有波动性?
哪些现象说明光具有粒子性?
什么时候呈现波动性?什么时候呈现粒子性?
例5.关于光的本性,下列说法中正确的是( )
A.关于光的本性,牛顿提出“微粒说”.惠更斯提出“波动说”,爱因斯坦提出“光子说”,它们都说明了光的本性
B.光具有波粒二象性是指:既可以把光看成宏观概念上的波,也可以看成微观概念上的粒子
C.光的干涉、衍射现象说明光具有波动性
D.光电效应说明光具有粒子性
例6.科学研究证明,光子有能量也有动量,当光子与电子碰撞时,光子的一些能量转移给了电子.假设光子与电子碰撞前的波长为λ,碰撞后的波长为λ′,则碰撞过程中( )
A.能量守恒,动量守恒,且λ=λ′
B.能量不守恒,动量不守恒,且λ=λ′
C.能量守恒,动量守恒,且λ<λ′
D.能量守恒,动量守恒,且λ>λ′
同课章节目录
- 第1章 分子动理论与气体实验定律
- 第1节 分子动理论的基本观点
- 第2节 科学测量:用油膜法估测油酸分子的大小
- 第3节 气体分子速率分布的统计规律
- 第4节 科学探究:气体压强与体积的关系
- 第5节 气体实验定律
- 第2章 固体与液体
- 第1节 固体类型及微观结构
- 第2节 表面张力和毛细现象
- 第3节 材料及其应用
- 第3章 热力学定律
- 第1节 热力学第一定律
- 第2节 能量的转化与守恒
- 第3节 热力学第二定律
- 第4节 熵——系统无序程度的量度
- 第4章 原子结构
- 第1节 电子的发现与汤姆孙原子模型
- 第2节 原子的核式结构模型
- 第3节 光谱与氢原子光谱
- 第4节 玻尔原子模型
- 第5章 原子核与核能
- 第1节 认识原子核
- 第2节 原子核衰变及半衰期
- 第3节 核力与核能
- 第4节 核裂变和核聚变
- 第5节 核能的利用与环境保护
- 第6章 波粒二象性
- 第1节 光电效应及其解释
- 第2节 实物粒子的波粒二象性
