第四章 投影与视图单元测试题(含答案)
文档属性
| 名称 | 第四章 投影与视图单元测试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 285.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-29 09:20:16 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第四章投影与视图
一、选择题(本大题共12个小题,在给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个,均记零分共36分)
1.如图是由4个相同的小正方形搭成的一个几何体,则它的俯视图是( )
A. B. C. D.
2.下列几何体各自的三视图中,只有两个视图相同的是( )
A. ①③ B. ②③ C. ③④ D. ②④
3.如果阳光斜射在地面上,一张矩形纸片在地面上的影子不可能是( )
A. 矩形 B. 线段 C. 平行四边形 D. 一个点
4.如图是由5个相同的小正方体构成的几何体,其主视图是( )
A. B. C. D.
5.在操场上练习双杠的过程中发现双杠的两横杠在地上的影子( )
A. 相交 B. 互相垂直 C. 互相平行 D. 无法确定
6.如图所示正三棱柱的主视图( )
A. B. C. D.
1
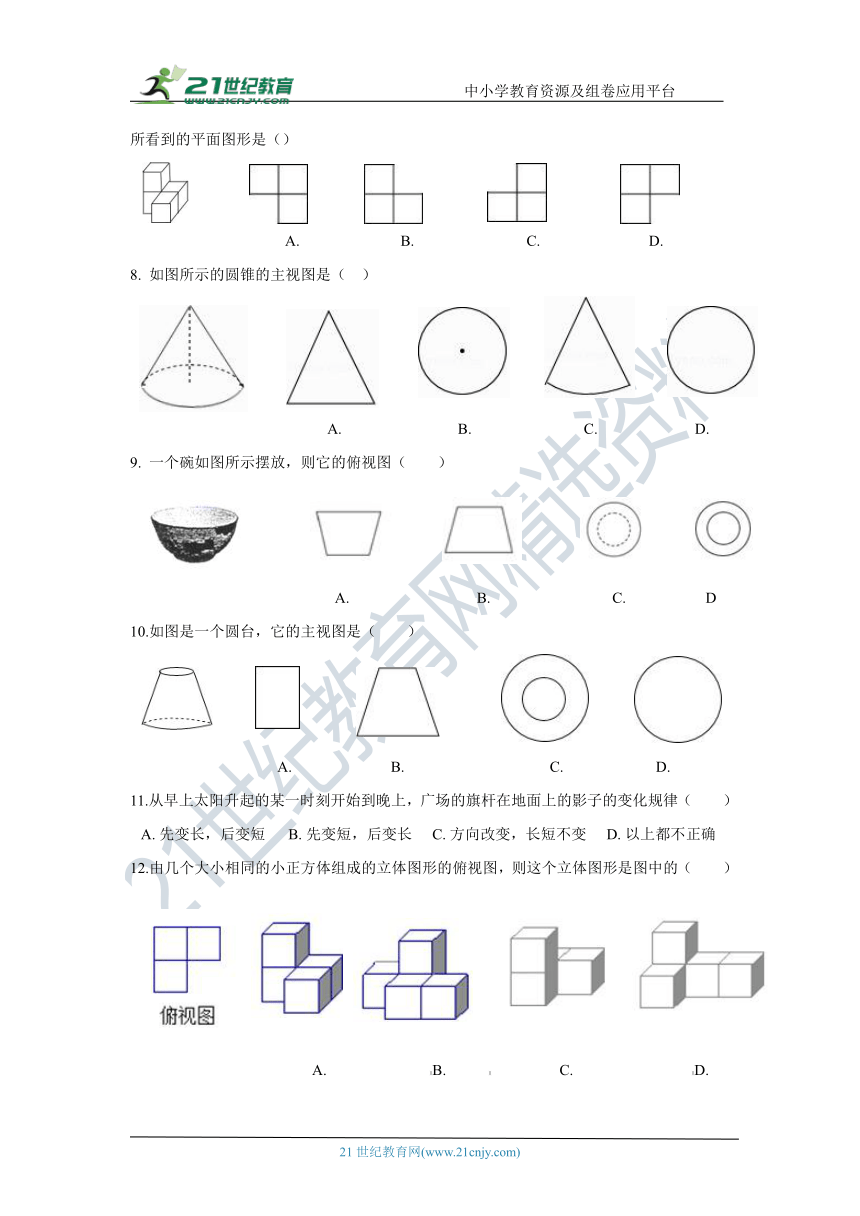
7.如图所示的几何体是由若干个大小相同的小正方体组成的.若从正上方看这个几何体,则所看到的平面图形是()
A. B. C. D.
8. 如图所示的圆锥的主视图是( )
A. B. C. D.
9. 一个碗如图所示摆放,则它的俯视图( )
A. B. C. D
10.如图是一个圆台,它的主视图是( )
A. B. C. D.
11.从早上太阳升起的某一时刻开始到晚上,广场的旗杆在地面上的影子的变化规律( )
A. 先变长,后变短 B. 先变短,后变长 C. 方向改变,长短不变 D. 以上都不正确
12.由几个大小相同的小正方体组成的立体图形的俯视图,则这个立体图形是图中的( )
A. B. C. D.
第Ⅱ卷(非选择题 84分)
2
二、填空题(本大题共6个小题,每小题3分,共18分)
13.长方体的主视图、俯视图如图,则其左视图面积为________ .
14. 如图,一根直立于水平地面的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5m,在旋转过程中,影长的最大值为5m,最小值3m,且影长最大时,木杆与光线垂直,则路灯EF的高度为________ m.
15.有底面为正方形的直四棱柱容器A和圆柱形容器B,容器材质相同,厚度忽略不计.如果它们的主视图是完全相同的矩形,那么将B容器盛满水,全部倒入A容器,问:结果会________ (“溢出”、“刚好”、“未装满”,选一个)
16.如果一个几何体的主视图和左视图都是等腰三角形,而且俯视图是一个圆,那么这个几何体是________ .
17.如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为________m.
18.人离窗子越远,向外眺望时此人的盲区是______
三、解答题(本大题共6个小题,满分66分,解答题应写出必要的文字说明或推演步骤)
19.(9分) 如图,一根竹竿如图所示,请画出它在太阳光下的影子.
20.(9分)如图是某种几何体的三视图,(1)这个几何体是什么;(2)若从正面看时,长方形的宽为10m,高为20m,试求此几何体的表面积是多少m2?(结果用π表示).
21.(11分) 如图,某校墙边有甲、乙两根木杆,已知乙木杆的高度为1.5m.
(1)某一时刻甲木杆在阳光下的影子如图,画出此时乙木
杆的影子DF
(2)△ABC∽△DEF,如果测得甲、乙木杆的影子长分别为1.6m和1m,
3
那么甲木杆的高度是多少?
22.(12分)如图是用相同的小正方体搭成的几何体的主视图、俯视图和左视图要搭成这样的几何体,
(1)最多需要几个小正方体?
(2)最少需要几个小正方体?
(3)当所需要的小正方体的个数最少时,有几种搭法?
23.(12分) 如图,在房子外的屋檐E处装有一台监视器,房子前面有一面落地的广告牌.
求:(1)画出监视器的盲区
(2)已知房子上的监视器离地面高12m,广告牌高6m,
广告牌距离房子5m,求盲区在地面上的长度.
24.(13分) 如图,高高的路灯挂在路边的上方,高傲而明亮,小明拿着一根2米长的竹竿,想量一量路灯的高度,直接量是不可能的.于是,他走到路灯旁的一个地方,竖起竹竿(即AE),这时,他量了一下竹竿的影长(AC)正好是1米,他沿着影子的方向走,向远处走出两根竹竿的长度(即AB=4米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即BD=2米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,我知道路灯有多高了!”同学们,请你和小明一起解答这个问题:
(1)在图中作出路灯O的位置,并作OP⊥l于P.
(2)求出路灯O的高度,并说明理由.
第四章投影与视图单元达标测试卷答案
一、选择题1-5 ADDAC 6-10 BAACB 11-12BC
二、填空题(本大题共4个小题,每小题3分,共12分。)
13. 3 14. 7.5 ;15. 未装满 16. 圆锥17. 3 18. 变大
三、解答题
19. 解:如图所示:
线段AB和BC的和即为竹竿的影子.
20.解:(1)根据图形得到几何体为:圆柱(2)表面积为:2(25π)+10π×20=250π(m2)
21解:如图所示,DF是乙木杆的影子
(2)∵△ABC∽△DEF, ∴=,解得AB=2.4m.答:甲木杆的高度是2.4m
22 解:(1)最多需要9+9+9=27个小正方体;(2)最少需要9+3+3=15个小正方体;
(3)当所需要的小正方体的个数最少时,有6种搭法.
23. 解: (1)把墙看做如图的线段,则如图,ABC所围成的部分就是监控不到的区域:
(2)由题意结合图形可得:BC为盲区,设BC=x,则CD=x+5,=,解得:x=5.
答:盲区在地面上的长度是5米.
24. 解:(1)如图所示
(2)由于BF=DB=2(米),即∠D=45°,∴DP=OP=灯高,在△COP中AE⊥CP,OP⊥CP,∴AE∥OP∴△CEA∽△COP,
即=,设AP=x,OP=h则:=①,DP=OP
表达为2+4+x=h②,联立①②两式得:x=4,h=10,∴路灯有10米高.
13题图
17题图
14题图
19题图
20题图
21题图
22题图
23题图
24题图
23题图
20题图
19题图
PAGE
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第四章投影与视图
一、选择题(本大题共12个小题,在给出的四个选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个,均记零分共36分)
1.如图是由4个相同的小正方形搭成的一个几何体,则它的俯视图是( )
A. B. C. D.
2.下列几何体各自的三视图中,只有两个视图相同的是( )
A. ①③ B. ②③ C. ③④ D. ②④
3.如果阳光斜射在地面上,一张矩形纸片在地面上的影子不可能是( )
A. 矩形 B. 线段 C. 平行四边形 D. 一个点
4.如图是由5个相同的小正方体构成的几何体,其主视图是( )
A. B. C. D.
5.在操场上练习双杠的过程中发现双杠的两横杠在地上的影子( )
A. 相交 B. 互相垂直 C. 互相平行 D. 无法确定
6.如图所示正三棱柱的主视图( )
A. B. C. D.
1
7.如图所示的几何体是由若干个大小相同的小正方体组成的.若从正上方看这个几何体,则所看到的平面图形是()
A. B. C. D.
8. 如图所示的圆锥的主视图是( )
A. B. C. D.
9. 一个碗如图所示摆放,则它的俯视图( )
A. B. C. D
10.如图是一个圆台,它的主视图是( )
A. B. C. D.
11.从早上太阳升起的某一时刻开始到晚上,广场的旗杆在地面上的影子的变化规律( )
A. 先变长,后变短 B. 先变短,后变长 C. 方向改变,长短不变 D. 以上都不正确
12.由几个大小相同的小正方体组成的立体图形的俯视图,则这个立体图形是图中的( )
A. B. C. D.
第Ⅱ卷(非选择题 84分)
2
二、填空题(本大题共6个小题,每小题3分,共18分)
13.长方体的主视图、俯视图如图,则其左视图面积为________ .
14. 如图,一根直立于水平地面的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5m,在旋转过程中,影长的最大值为5m,最小值3m,且影长最大时,木杆与光线垂直,则路灯EF的高度为________ m.
15.有底面为正方形的直四棱柱容器A和圆柱形容器B,容器材质相同,厚度忽略不计.如果它们的主视图是完全相同的矩形,那么将B容器盛满水,全部倒入A容器,问:结果会________ (“溢出”、“刚好”、“未装满”,选一个)
16.如果一个几何体的主视图和左视图都是等腰三角形,而且俯视图是一个圆,那么这个几何体是________ .
17.如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为________m.
18.人离窗子越远,向外眺望时此人的盲区是______
三、解答题(本大题共6个小题,满分66分,解答题应写出必要的文字说明或推演步骤)
19.(9分) 如图,一根竹竿如图所示,请画出它在太阳光下的影子.
20.(9分)如图是某种几何体的三视图,(1)这个几何体是什么;(2)若从正面看时,长方形的宽为10m,高为20m,试求此几何体的表面积是多少m2?(结果用π表示).
21.(11分) 如图,某校墙边有甲、乙两根木杆,已知乙木杆的高度为1.5m.
(1)某一时刻甲木杆在阳光下的影子如图,画出此时乙木
杆的影子DF
(2)△ABC∽△DEF,如果测得甲、乙木杆的影子长分别为1.6m和1m,
3
那么甲木杆的高度是多少?
22.(12分)如图是用相同的小正方体搭成的几何体的主视图、俯视图和左视图要搭成这样的几何体,
(1)最多需要几个小正方体?
(2)最少需要几个小正方体?
(3)当所需要的小正方体的个数最少时,有几种搭法?
23.(12分) 如图,在房子外的屋檐E处装有一台监视器,房子前面有一面落地的广告牌.
求:(1)画出监视器的盲区
(2)已知房子上的监视器离地面高12m,广告牌高6m,
广告牌距离房子5m,求盲区在地面上的长度.
24.(13分) 如图,高高的路灯挂在路边的上方,高傲而明亮,小明拿着一根2米长的竹竿,想量一量路灯的高度,直接量是不可能的.于是,他走到路灯旁的一个地方,竖起竹竿(即AE),这时,他量了一下竹竿的影长(AC)正好是1米,他沿着影子的方向走,向远处走出两根竹竿的长度(即AB=4米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即BD=2米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,我知道路灯有多高了!”同学们,请你和小明一起解答这个问题:
(1)在图中作出路灯O的位置,并作OP⊥l于P.
(2)求出路灯O的高度,并说明理由.
第四章投影与视图单元达标测试卷答案
一、选择题1-5 ADDAC 6-10 BAACB 11-12BC
二、填空题(本大题共4个小题,每小题3分,共12分。)
13. 3 14. 7.5 ;15. 未装满 16. 圆锥17. 3 18. 变大
三、解答题
19. 解:如图所示:
线段AB和BC的和即为竹竿的影子.
20.解:(1)根据图形得到几何体为:圆柱(2)表面积为:2(25π)+10π×20=250π(m2)
21解:如图所示,DF是乙木杆的影子
(2)∵△ABC∽△DEF, ∴=,解得AB=2.4m.答:甲木杆的高度是2.4m
22 解:(1)最多需要9+9+9=27个小正方体;(2)最少需要9+3+3=15个小正方体;
(3)当所需要的小正方体的个数最少时,有6种搭法.
23. 解: (1)把墙看做如图的线段,则如图,ABC所围成的部分就是监控不到的区域:
(2)由题意结合图形可得:BC为盲区,设BC=x,则CD=x+5,=,解得:x=5.
答:盲区在地面上的长度是5米.
24. 解:(1)如图所示
(2)由于BF=DB=2(米),即∠D=45°,∴DP=OP=灯高,在△COP中AE⊥CP,OP⊥CP,∴AE∥OP∴△CEA∽△COP,
即=,设AP=x,OP=h则:=①,DP=OP
表达为2+4+x=h②,联立①②两式得:x=4,h=10,∴路灯有10米高.
13题图
17题图
14题图
19题图
20题图
21题图
22题图
23题图
24题图
23题图
20题图
19题图
PAGE
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
