因式分解[上学期]
图片预览







文档简介
课件21张PPT。因式分解——运用公式法温故而知新 计算:
(1) (a+1) (a-1)
(2) (-2x-3y) (2x-3y)
(3) 99.7 ×100.3
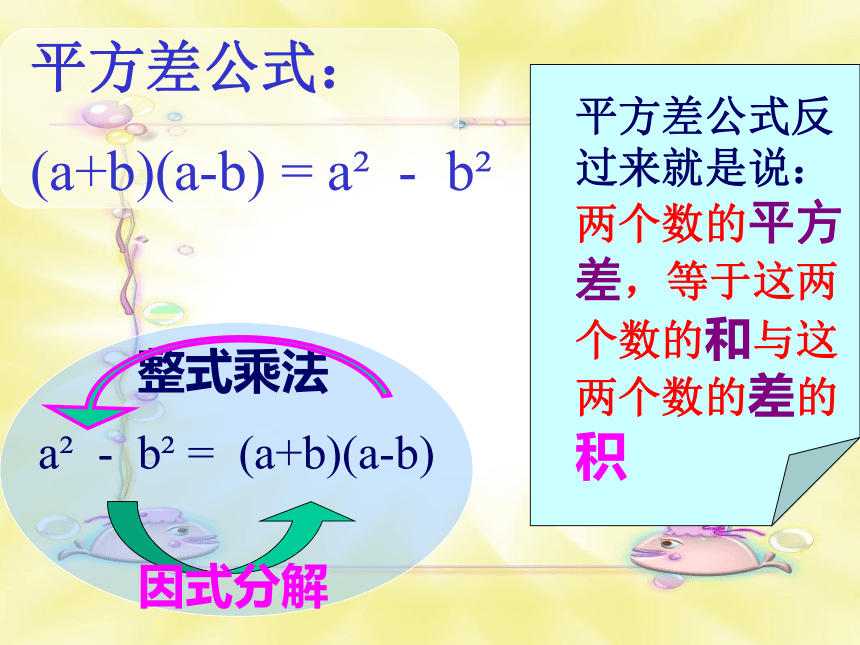
(4) 20062-20052平方差公式:
(a+b)(a-b) = a2-b2整式乘法看谁做得最快最正确!因式分解的定义: 复习回顾 把一个多项式写成
几个整式的积的形式,
叫做多项式的因式分解.3、x2-25 = _____(x-5) (x+5)a2-b2 2、(a+b) (a-b) = _____在横线上填上适当的式子,使等号成立:x2-25 1、(x+5) (x-5) = _____4、a2-b2 = (a+b)_____ (a-b)第⑴、⑵两式从左到右是什么形式?第⑶、⑷两式从左到右是什么形式?情境创设整式乘法因式分解平方差公式反过来就是说:两个数的平方差,等于这两个数的和与这两个数的差的积a2 - b2 = (a+b)(a-b)
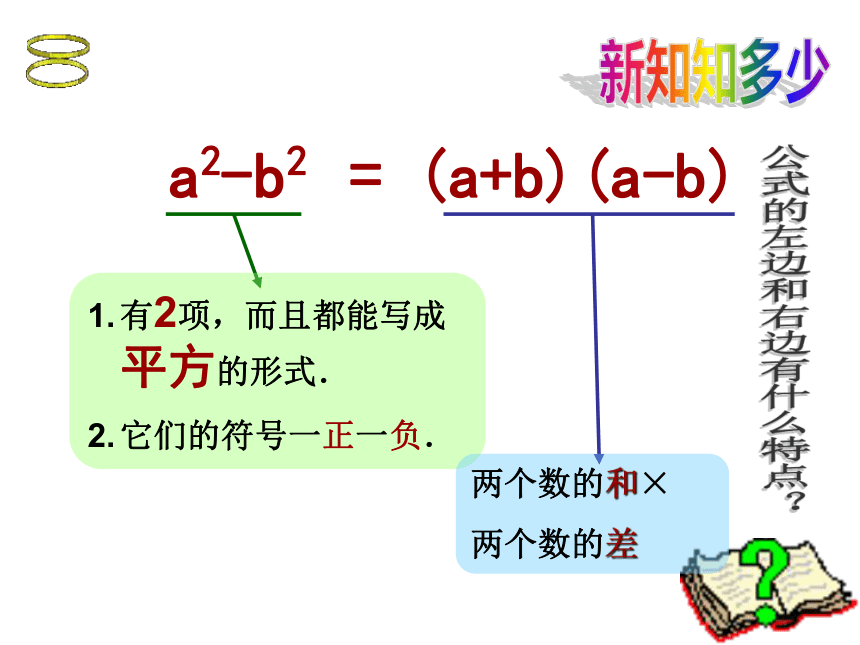
因式分解平方差公式:
(a+b)(a-b) = a2 - b2整式乘法a2-b2 = (a+b)(a-b) 新知知多少公式的左边和右边有什么特点?做一做: a2–16 = a2 –( )2 =(a + )(a - ) 64- b2= ( )2 –b2 = ( + b )( - b ) 48问题把下列各式分解因式
(1) x2 - 1开始抢答平方差公式:
a2-b2 =(a+b)(a-b)(2) m2 - 9(3) x2 - 4y2=(x+1)(x-1)=(m+3)(m-3)=(x+2y)(x-2y) 下列各式中,能用平方差公式分解因式的有: a2+b2
-a2-b2
a2-b2
(4) -a2+b2(3)(4)例1:把下列各式分解因式:
(1)36 –25x2
(2)16a2–9b2
(3)9(a+b)2–4(a-b)2
答案:
36 –25x2 =
16a2–9b2 =
(3) 9(a+b)2–4(a-b)2 62 –(5x)2= (6 +5x)(6 –5x)(4a)2 –(3b)2= (4a +3b)(4a –3b)=[3(a+b)]2 –[2(a-b)]2= {[3(a+b)] +[2(a-b)] }{[3(a+b)] –[2(a-b)]}= (5a+b)(a+5b)练习: 把下列各式分解因式:解:原式= m2 - (5x)2=(m+5x) (m-5x)原式=(ab)2 - (2x)2=(ab+2x) (ab-2x)(1) m2-25n2 (2) a2b2-4x2把下列各式分解因式
(1) 4a2 - 1开始抢答平方差公式:
a2-b2 =(a+b)(a-b)(2) x2 - y2(3) 4a2 - 25b2=(2a+1)(2a-1)=(x+y)(x-y)=(2a+5b)(2a-5b)(4) b2 - 16=(b+4)(b-4)(5) 512 - 492=(51+49)(51-49)=200=(3a+2)(3a-2)(6) 9 a2 - 4例2 分解因式:-9m2+16n2解:原式= 16n2 - 9m2=(4n)2 - (3m)2
=(4n +3m)(4n-3m)练习:用平方差公式分解因式:
(1) -4+9a2
(2) -36y2+25x2平方差公式:
a2-b2 =(a+b)(a-b)例3.把下列各式分解因式
① x4 - 81y4
② 2a3 - 8a
2.解:原式=2a(a2- 4)
=2a(a+2)(a-2)1.解:原式=(x2)2-(9y2)2
= (x2+ 9y2) (x2- 9y2)
= (x2+ 9y2) (x+ 3y) (x- 3y)练习 :(1)x4 – y4
(2) -x4 +16y4用平方差公式进行简便计算:
382-372 2) 2132-872
3) 2292-1712 4) 91×89
解:1) 382-372
=(38+37)(38-37)=752132-872
=(213+87)(213-87)
=300×126=37800解:3) 2292-1712
=(229+171)(229-171)=400×58=23200解:4) 91×89
=(90+1)(90-1)
=902-1=8100-1=8099课堂聚焦1.先提取公因式2.再应用平方差公式分解3.每个因式要化简,并且分解彻底对于分解复杂的多项式,我们应该怎么做?a2-b2 = (a+b)(a-b) 你说,我说,大家说!注意:1.平方差公式2、能写成( )2-( )2的式子,可以用平方差公式分解因式。3、公式中的a,b可以是单独的数字、字母,也可以是单项式、多项式。4、分解因式,应进行到每一个多项式因式不能再分解为止。a2-b2 = (a+b)(a-b) 巩固练习作业把下列各式因式分解:(1) 25x2-4 (2) 121 - 4a2b4
(3) a4 - 4b4 (4) -x2+49y2
(5) 3m3-12mn4 (6)
(7)再见
(1) (a+1) (a-1)
(2) (-2x-3y) (2x-3y)
(3) 99.7 ×100.3
(4) 20062-20052平方差公式:
(a+b)(a-b) = a2-b2整式乘法看谁做得最快最正确!因式分解的定义: 复习回顾 把一个多项式写成
几个整式的积的形式,
叫做多项式的因式分解.3、x2-25 = _____(x-5) (x+5)a2-b2 2、(a+b) (a-b) = _____在横线上填上适当的式子,使等号成立:x2-25 1、(x+5) (x-5) = _____4、a2-b2 = (a+b)_____ (a-b)第⑴、⑵两式从左到右是什么形式?第⑶、⑷两式从左到右是什么形式?情境创设整式乘法因式分解平方差公式反过来就是说:两个数的平方差,等于这两个数的和与这两个数的差的积a2 - b2 = (a+b)(a-b)
因式分解平方差公式:
(a+b)(a-b) = a2 - b2整式乘法a2-b2 = (a+b)(a-b) 新知知多少公式的左边和右边有什么特点?做一做: a2–16 = a2 –( )2 =(a + )(a - ) 64- b2= ( )2 –b2 = ( + b )( - b ) 48问题把下列各式分解因式
(1) x2 - 1开始抢答平方差公式:
a2-b2 =(a+b)(a-b)(2) m2 - 9(3) x2 - 4y2=(x+1)(x-1)=(m+3)(m-3)=(x+2y)(x-2y) 下列各式中,能用平方差公式分解因式的有: a2+b2
-a2-b2
a2-b2
(4) -a2+b2(3)(4)例1:把下列各式分解因式:
(1)36 –25x2
(2)16a2–9b2
(3)9(a+b)2–4(a-b)2
答案:
36 –25x2 =
16a2–9b2 =
(3) 9(a+b)2–4(a-b)2 62 –(5x)2= (6 +5x)(6 –5x)(4a)2 –(3b)2= (4a +3b)(4a –3b)=[3(a+b)]2 –[2(a-b)]2= {[3(a+b)] +[2(a-b)] }{[3(a+b)] –[2(a-b)]}= (5a+b)(a+5b)练习: 把下列各式分解因式:解:原式= m2 - (5x)2=(m+5x) (m-5x)原式=(ab)2 - (2x)2=(ab+2x) (ab-2x)(1) m2-25n2 (2) a2b2-4x2把下列各式分解因式
(1) 4a2 - 1开始抢答平方差公式:
a2-b2 =(a+b)(a-b)(2) x2 - y2(3) 4a2 - 25b2=(2a+1)(2a-1)=(x+y)(x-y)=(2a+5b)(2a-5b)(4) b2 - 16=(b+4)(b-4)(5) 512 - 492=(51+49)(51-49)=200=(3a+2)(3a-2)(6) 9 a2 - 4例2 分解因式:-9m2+16n2解:原式= 16n2 - 9m2=(4n)2 - (3m)2
=(4n +3m)(4n-3m)练习:用平方差公式分解因式:
(1) -4+9a2
(2) -36y2+25x2平方差公式:
a2-b2 =(a+b)(a-b)例3.把下列各式分解因式
① x4 - 81y4
② 2a3 - 8a
2.解:原式=2a(a2- 4)
=2a(a+2)(a-2)1.解:原式=(x2)2-(9y2)2
= (x2+ 9y2) (x2- 9y2)
= (x2+ 9y2) (x+ 3y) (x- 3y)练习 :(1)x4 – y4
(2) -x4 +16y4用平方差公式进行简便计算:
382-372 2) 2132-872
3) 2292-1712 4) 91×89
解:1) 382-372
=(38+37)(38-37)=752132-872
=(213+87)(213-87)
=300×126=37800解:3) 2292-1712
=(229+171)(229-171)=400×58=23200解:4) 91×89
=(90+1)(90-1)
=902-1=8100-1=8099课堂聚焦1.先提取公因式2.再应用平方差公式分解3.每个因式要化简,并且分解彻底对于分解复杂的多项式,我们应该怎么做?a2-b2 = (a+b)(a-b) 你说,我说,大家说!注意:1.平方差公式2、能写成( )2-( )2的式子,可以用平方差公式分解因式。3、公式中的a,b可以是单独的数字、字母,也可以是单项式、多项式。4、分解因式,应进行到每一个多项式因式不能再分解为止。a2-b2 = (a+b)(a-b) 巩固练习作业把下列各式因式分解:(1) 25x2-4 (2) 121 - 4a2b4
(3) a4 - 4b4 (4) -x2+49y2
(5) 3m3-12mn4 (6)
(7)再见
