2.5三角函数的应用(1) 课件(9张PPT)
文档属性
| 名称 | 2.5三角函数的应用(1) 课件(9张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 376.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-27 17:07:48 | ||
图片预览



文档简介
(共9张PPT)
鲁教版数学九年级上册第二章第五节
2.5三角函数的应用(1)
1.了解仰角、俯角的意义。
2.能应用解直角三角形的知识解决实际问题.
tanA=
b
a
∠A + ∠B = 90 °;
a2+b2=c2 ;
(3)角与边之间的关系:
(2)边之间的关系:
(1)角之间的关系:
sinA=
c
a
,
cosA=
c
b
,
2. 如果知道直角三角形的几个元素就可以求其他的元素?
有几种情况?
两个元素(至少一个是边)
两条边或一边一角
1.直角三角形的边角关系:
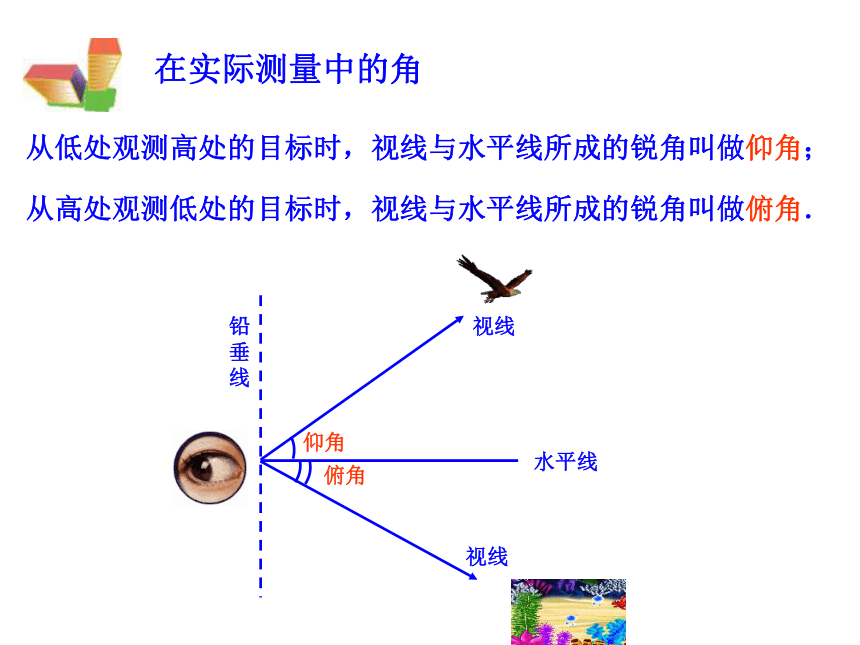
铅垂线
水平线
仰角
俯角
在实际测量中的角
视线
视线
从高处观测低处的目标时,视线与水平线所成的锐角叫做俯角.
从低处观测高处的目标时,视线与水平线所成的锐角叫做仰角;
A
B
C
(
α
例1 如图,一架直升飞机执行海上搜救任务,在空中A 处发现海面上有一目标B ,仪器显示这时飞机的高度为1.5km,飞机距目标4.5km。
求飞机在A处观测目标B的俯角(精确到1 ' ).
甲、乙两幢楼,从甲楼底部B处测得乙楼顶部C的仰角为45 ,从乙楼顶部C测得甲楼顶部A的俯角为30 ;已知甲、乙两楼的距离BD=60m,求甲、乙两楼的高。
例2 武汉长江二桥为斜拉索桥,AB和AC,分别是直立塔AD左右两边的两根最长的钢索。已知AB=AC,BC =100m,AB与BC的夹角为30°。求钢索AB的长及直立塔AD的高.
A
B
D
C
30°
1.菱形ABCD的对角形AC=10cm,BD=6cm,那
么 =------.
2.等腰三角形底边长10cm,周长为36cm,那么底角的余弦等于---------.
3.会根据题意把实际问题转化为数学问题,然后利用解直角三角形的知识,明确已知量和未知量,选择合适的三角比,从而求得未知量.
2.从高处观测低处的目标时,视线与水平线所成的锐角叫做俯角.
1.从低处观测高处的目标时,视线与水平线所成的锐角叫做仰角;
鲁教版数学九年级上册第二章第五节
2.5三角函数的应用(1)
1.了解仰角、俯角的意义。
2.能应用解直角三角形的知识解决实际问题.
tanA=
b
a
∠A + ∠B = 90 °;
a2+b2=c2 ;
(3)角与边之间的关系:
(2)边之间的关系:
(1)角之间的关系:
sinA=
c
a
,
cosA=
c
b
,
2. 如果知道直角三角形的几个元素就可以求其他的元素?
有几种情况?
两个元素(至少一个是边)
两条边或一边一角
1.直角三角形的边角关系:
铅垂线
水平线
仰角
俯角
在实际测量中的角
视线
视线
从高处观测低处的目标时,视线与水平线所成的锐角叫做俯角.
从低处观测高处的目标时,视线与水平线所成的锐角叫做仰角;
A
B
C
(
α
例1 如图,一架直升飞机执行海上搜救任务,在空中A 处发现海面上有一目标B ,仪器显示这时飞机的高度为1.5km,飞机距目标4.5km。
求飞机在A处观测目标B的俯角(精确到1 ' ).
甲、乙两幢楼,从甲楼底部B处测得乙楼顶部C的仰角为45 ,从乙楼顶部C测得甲楼顶部A的俯角为30 ;已知甲、乙两楼的距离BD=60m,求甲、乙两楼的高。
例2 武汉长江二桥为斜拉索桥,AB和AC,分别是直立塔AD左右两边的两根最长的钢索。已知AB=AC,BC =100m,AB与BC的夹角为30°。求钢索AB的长及直立塔AD的高.
A
B
D
C
30°
1.菱形ABCD的对角形AC=10cm,BD=6cm,那
么 =------.
2.等腰三角形底边长10cm,周长为36cm,那么底角的余弦等于---------.
3.会根据题意把实际问题转化为数学问题,然后利用解直角三角形的知识,明确已知量和未知量,选择合适的三角比,从而求得未知量.
2.从高处观测低处的目标时,视线与水平线所成的锐角叫做俯角.
1.从低处观测高处的目标时,视线与水平线所成的锐角叫做仰角;
