5.3垂径定理 课件(13张PPT)
图片预览


文档简介
(共13张PPT)
§5.3垂径定理
鲁教版 九年级(下)第五章 圆
学习目标
1.经历探索圆的对称性及有关性质的过程.
2.理解圆的对称性及有关性质.
3.会垂径定理解决有关问题.
③AM=BM,
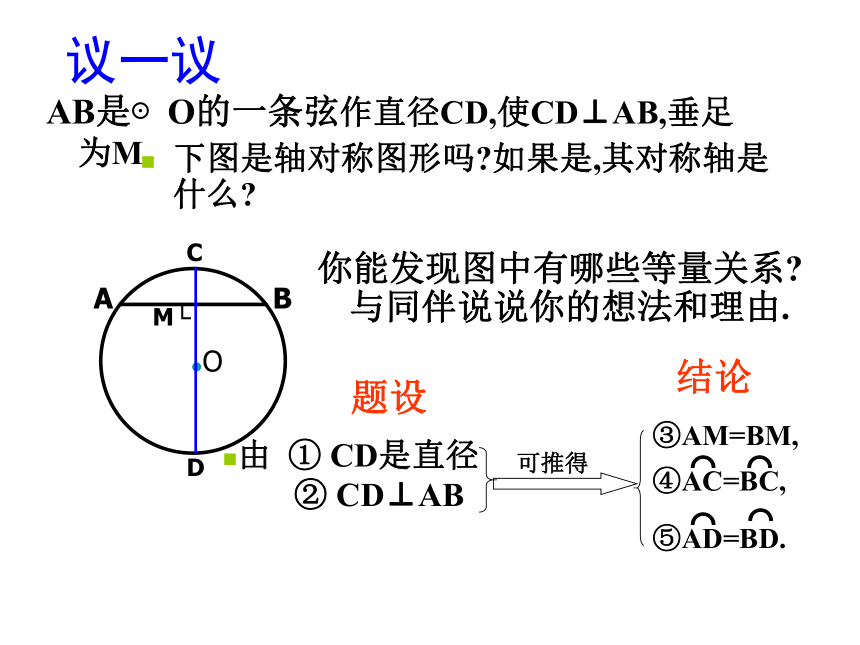
议一议
AB是⊙O的一条弦作直径CD,使CD⊥AB,垂足为M.
你能发现图中有哪些等量关系 与同伴说说你的想法和理由.
●O
下图是轴对称图形吗 如果是,其对称轴是什么
A
B
C
D
M└
由 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
题设
结论
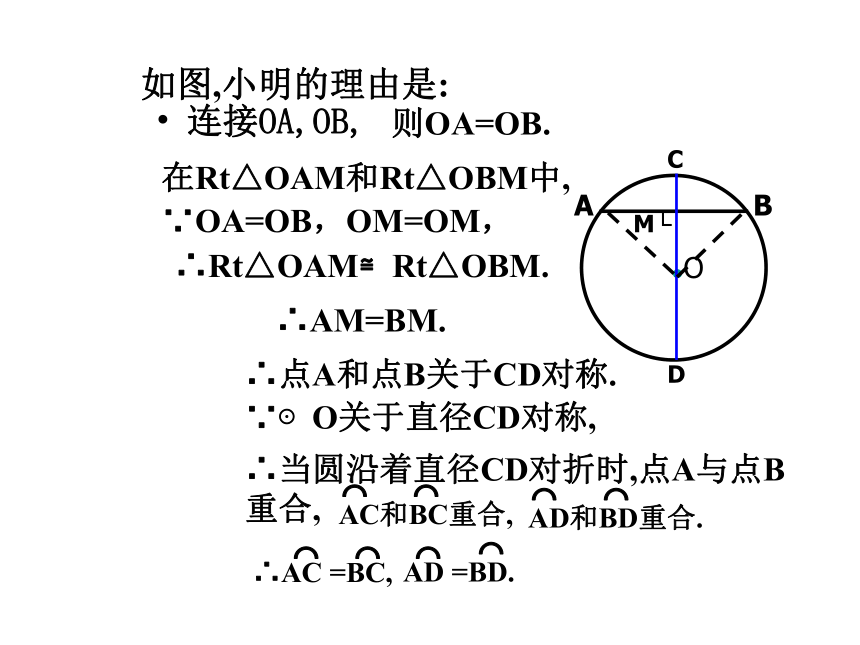
如图,小明的理由是:
连接OA,OB,
●O
A
B
C
D
M└
则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB,OM=OM,
∴Rt△OAM≌Rt△OBM.
∴AM=BM.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
⌒
⌒
AC和BC重合,
⌒
⌒
AD和BD重合.
⌒
⌒
∴AC =BC,
⌒
⌒
AD =BD.
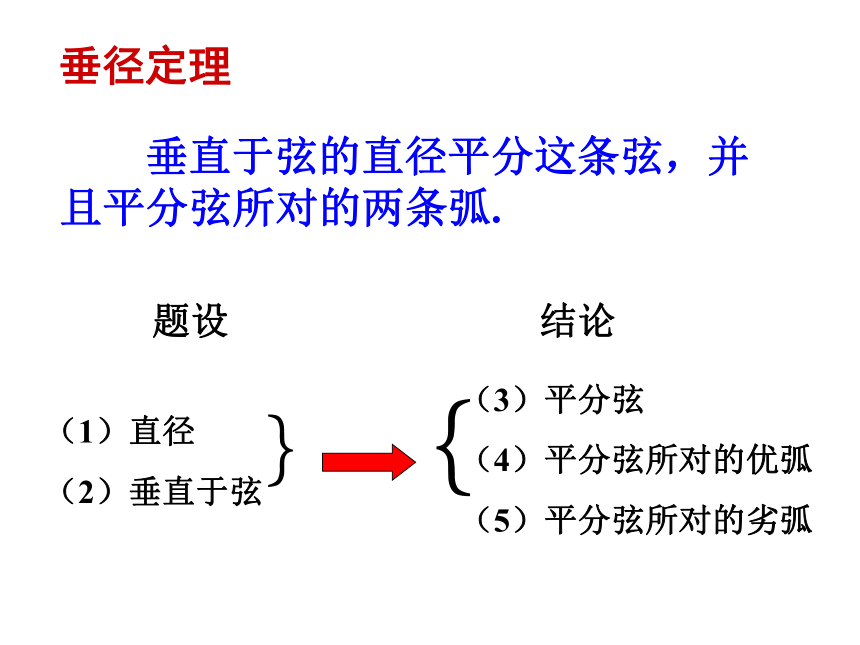
垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
题设
结论
(1)直径
(2)垂直于弦
}
{
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
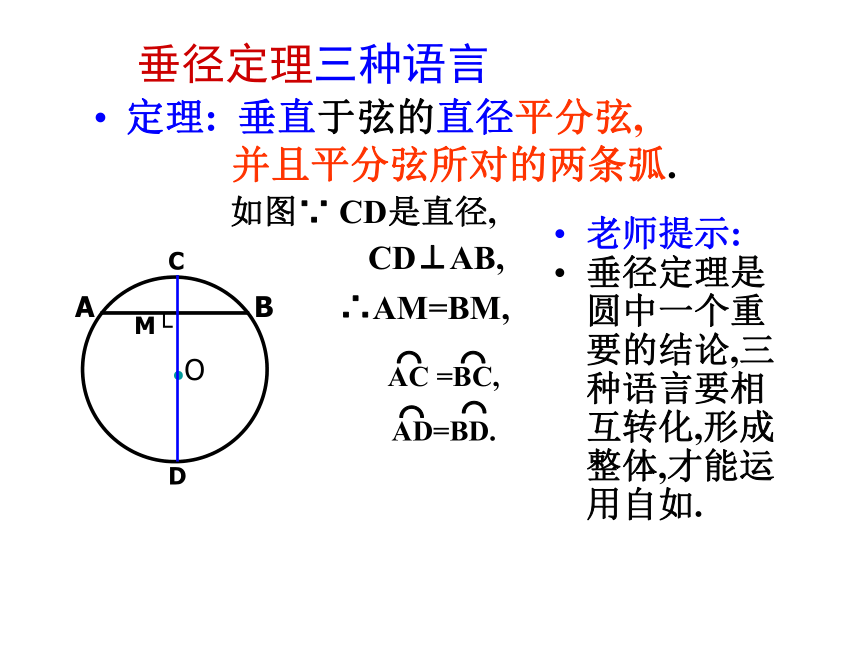
垂径定理三种语言
定理: 垂直于弦的直径平分弦,
并且平分弦所对的两条弧.
老师提示:
垂径定理是圆中一个重要的结论,三种语言要相互转化,形成整体,才能运用自如.
●O
A
B
C
D
M└
CD⊥AB,
如图∵ CD是直径,
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
在下列图形中,你能否利用垂径定理找到相等的线段或相等的圆弧
如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径.
E
.
A
B
O
典例精讲
已知:如图,⊙O 中, AB为 弦,C 为
弧AB 的中点,OC交AB 于D ,AB = 6cm ,
CD = 1cm. 求⊙O 的半径OA.
做一做
M
O
A
C
B
N
①直线MN过圆心③ AC=BC
②MN⊥AB
④弧AM=弧BM ⑤弧AN=弧BN
探索一:
结论:
O
A
B
M
N
一个圆的任意两条直径总是互相平分,但是它们不一定互相垂直。因此这里的弦如果是直径,结论就不一定成立。
推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
C
D
挑战自我画一画
如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.
●O
●M
⑴垂直于弦的直线平分弦,并且平分弦所对的弧( )
⑵弦所对的两弧中点的连线,垂直于弦,并且经过圆心 ( )
⑶圆的不与直径垂直的弦必不被这条直径平分 ( )
⑷平分弦的直径垂直于弦,并且平分弦所对的两条弧 ( )
⑸圆内两条非直径的弦不能互相平分( )
当堂达标
§5.3垂径定理
鲁教版 九年级(下)第五章 圆
学习目标
1.经历探索圆的对称性及有关性质的过程.
2.理解圆的对称性及有关性质.
3.会垂径定理解决有关问题.
③AM=BM,
议一议
AB是⊙O的一条弦作直径CD,使CD⊥AB,垂足为M.
你能发现图中有哪些等量关系 与同伴说说你的想法和理由.
●O
下图是轴对称图形吗 如果是,其对称轴是什么
A
B
C
D
M└
由 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
题设
结论
如图,小明的理由是:
连接OA,OB,
●O
A
B
C
D
M└
则OA=OB.
在Rt△OAM和Rt△OBM中,
∵OA=OB,OM=OM,
∴Rt△OAM≌Rt△OBM.
∴AM=BM.
∴点A和点B关于CD对称.
∵⊙O关于直径CD对称,
∴当圆沿着直径CD对折时,点A与点B重合,
⌒
⌒
AC和BC重合,
⌒
⌒
AD和BD重合.
⌒
⌒
∴AC =BC,
⌒
⌒
AD =BD.
垂径定理
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
题设
结论
(1)直径
(2)垂直于弦
}
{
(3)平分弦
(4)平分弦所对的优弧
(5)平分弦所对的劣弧
垂径定理三种语言
定理: 垂直于弦的直径平分弦,
并且平分弦所对的两条弧.
老师提示:
垂径定理是圆中一个重要的结论,三种语言要相互转化,形成整体,才能运用自如.
●O
A
B
C
D
M└
CD⊥AB,
如图∵ CD是直径,
∴AM=BM,
⌒
⌒
AC =BC,
⌒
⌒
AD=BD.
在下列图形中,你能否利用垂径定理找到相等的线段或相等的圆弧
如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径.
E
.
A
B
O
典例精讲
已知:如图,⊙O 中, AB为 弦,C 为
弧AB 的中点,OC交AB 于D ,AB = 6cm ,
CD = 1cm. 求⊙O 的半径OA.
做一做
M
O
A
C
B
N
①直线MN过圆心③ AC=BC
②MN⊥AB
④弧AM=弧BM ⑤弧AN=弧BN
探索一:
结论:
O
A
B
M
N
一个圆的任意两条直径总是互相平分,但是它们不一定互相垂直。因此这里的弦如果是直径,结论就不一定成立。
推论
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
C
D
挑战自我画一画
如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且AM=BM.
●O
●M
⑴垂直于弦的直线平分弦,并且平分弦所对的弧( )
⑵弦所对的两弧中点的连线,垂直于弦,并且经过圆心 ( )
⑶圆的不与直径垂直的弦必不被这条直径平分 ( )
⑷平分弦的直径垂直于弦,并且平分弦所对的两条弧 ( )
⑸圆内两条非直径的弦不能互相平分( )
当堂达标
