第八章 二元一次方程组——应用题练习(含解析)人教版数学七年级下册
文档属性
| 名称 | 第八章 二元一次方程组——应用题练习(含解析)人教版数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 212.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-29 20:59:53 | ||
图片预览




文档简介
二元一次方程组的应用题
一.选择题
1.利用两块相同的长方体木块测量一张桌子的高度.首先按图1方式放置,再交换两木块的位置,按图2方式放置.测量的数据如图,则桌子的高度是( )
A.73cm B.74cm C.75cm D.76cm
2.同型号的甲、乙两辆车加满气体燃料后均可行驶210km,它们各自单独行驶并返回的最远距离是105km.现在它们都从A地出发,行驶途中停下来从甲车的气体燃料桶抽一些气体燃料注入乙车的气体燃料桶,然后甲车再行驶返回A地,而乙车继续行驶,到B地后再行驶返回A地.则B地最远可距离A地( )
A.120km B.140km C.160km D.180km
3.利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式放置,再交换两木块的位置,按图②所示的方式放置.测量的数据如图,则桌子的高度等于( )
A.80cm B.75cm C.70cm D.65cm
4.某种高端品牌的家用电器,若按标价打八折销售该电器一件,则可获利润500元,其利润率为20%.现如果按同一标价打九折销售该电器一件,那么获得的纯利润为( )
A.562.5元 B.875元 C.550元 D.750元
5.甲、乙两人分别从相距40千米的两地同时出发,若同向而行,则5小时后,快者追上慢者;若相向而行,则2小时后,两人相遇,那么快者速度和慢者速度(单位:千米/小时)分别是( )
A.14和6 B.24和16 C.28和12 D.30和10
6.小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图(1);小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图(2)那样的正方形,中间还留下了一个洞,恰好是边长为3mm的小正方形,则每个小长方形的面积为( )
A.120mm2 B.135mm2 C.108mm2 D.96mm2
7.一道来自课本的习题:
从甲地到乙地有一段上坡与一段平路.如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min.甲地到乙地全程是多少?
小红将这个实际问题转化为二元一次方程组问题,设未知数x,y,已经列出一个方程+=,则另一个方程正确的是( )
A.+= B.+= C.+= D.+=
8.《九章算术》第七卷“盈不足”中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”译为:“今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又差4钱.问人数、物价各多少?”根据所学知识,计算出人数、物价分别是( )
A.1,11 B.7,53 C.7,61 D.6,50
9.如图,在长方形ABCD中,放入六个形状大小相同的长方形,所标尺寸如图所示,则图中阴影部分面积为( )
A.44cm2 B.36cm2 C.96cm2 D.84cm2
二.填空题
10.一个自行车轮胎,若把它安装在前轮,则自行车行驶5000km后报废;若把它安装在后轮,则自行车行驶3000km后报废,行驶一定路程后可以交换前、后轮胎.如果交换前、后轮胎,要使一辆自行车的一对新轮胎同时报废,那么这辆车将能行驶 km.
11.一个两位数的数字和为14,若调换个位数字与十位数字,新数比原数小36,则这个两位数是 .
12.现有八个大小相同的长方形,可拼成如图1、2所示的图形,在拼图2时,中间留下了一个边长为2的小正方形,则每个小长方形的长是 .
13.新学期伊始,西大附中的学子们积极响应学校的“书香校园”活动,踊跃捐出自己喜爱的书籍,互相分享,让阅读成为一种习惯.据调查,某年级甲班、乙班共80人捐书,丙班有40人捐书,已知乙班人均捐书数量比甲班人均捐书数量多5本,而丙班的人均捐书数量是甲班人均捐书数量的一半,若该年级甲、乙、丙三班的人均捐书数量恰好是乙班人均捐书数量的,且各班人均捐书数量均为正整数,则甲、乙、丙三班共捐书 本.
14.假设北碚万达广场地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为75%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.2019年元旦节期间,由于商场人数增多,早晨6点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过 小时车库恰好停满.
15.如图,长为4a的长方形,沿图中虚线裁剪成四个形状大小完全相同的小长方形,那么每个小长方形的周长为 (用含a的代数式表示).
16.我国明代数学读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托.如果1托为5尺,那么索长为 尺,竿子长为 尺.
17.一个两位数,十位数字比个位数字大3,若将十位数字和个位数交换位置,所得的新两位数比原两位数的多15,则这个两位数是 .
18.一天,小民去问爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生呢,你若是我现在这么大,我已经是老寿星了,125岁了,哈哈!”请你写出小民爷爷到底是 岁.
三.解答题
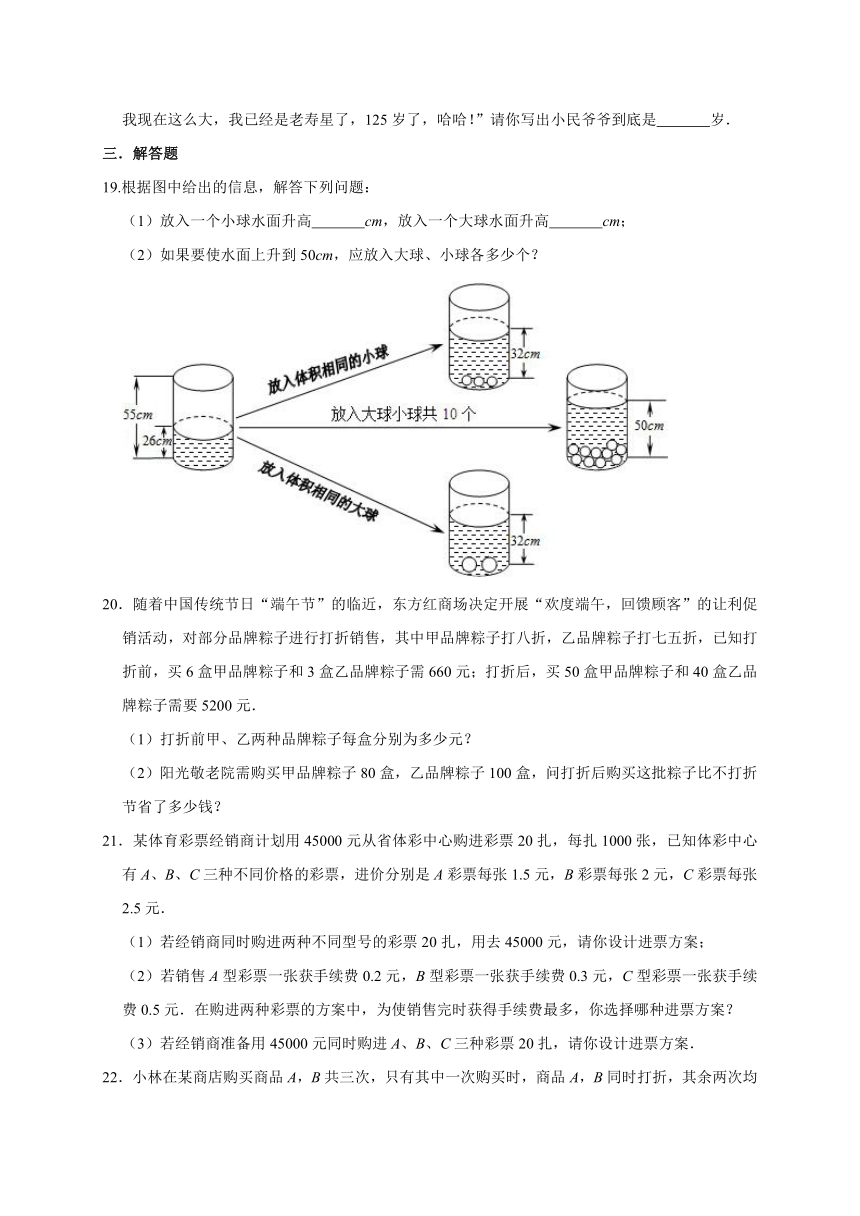
19.根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高 cm,放入一个大球水面升高 cm;
(2)如果要使水面上升到50cm,应放入大球、小球各多少个?
20.随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
21.某体育彩票经销商计划用45000元从省体彩中心购进彩票20扎,每扎1000张,已知体彩中心有A、B、C三种不同价格的彩票,进价分别是A彩票每张1.5元,B彩票每张2元,C彩票每张2.5元.
(1)若经销商同时购进两种不同型号的彩票20扎,用去45000元,请你设计进票方案;
(2)若销售A型彩票一张获手续费0.2元,B型彩票一张获手续费0.3元,C型彩票一张获手续费0.5元.在购进两种彩票的方案中,为使销售完时获得手续费最多,你选择哪种进票方案?
(3)若经销商准备用45000元同时购进A、B、C三种彩票20扎,请你设计进票方案.
22.小林在某商店购买商品A,B共三次,只有其中一次购买时,商品A,B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如表所示,
购买商品A的数量/个 购买商品B的数量/个 购买总费用/元
第一次购物 6 5 1140
第二次购物 3 7 1110
第三次购物 9 8 1062
(1)在这三次购物中,第 次购物打了折扣;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
二元一次方程组的应用题
参考答案与试题解析
一.选择题
1.利用两块相同的长方体木块测量一张桌子的高度.首先按图1方式放置,再交换两木块的位置,按图2方式放置.测量的数据如图,则桌子的高度是( )
A.73cm B.74cm C.75cm D.76cm
【解答】解:设长方体长xcm,宽ycm,桌子的高为acm,由题意,得
,
解得:2a=152,
∴a=76.
故选:D.
2.同型号的甲、乙两辆车加满气体燃料后均可行驶210km,它们各自单独行驶并返回的最远距离是105km.现在它们都从A地出发,行驶途中停下来从甲车的气体燃料桶抽一些气体燃料注入乙车的气体燃料桶,然后甲车再行驶返回A地,而乙车继续行驶,到B地后再行驶返回A地.则B地最远可距离A地( )
A.120km B.140km C.160km D.180km
【解答】解:设甲行驶到C地时返回,到达A地燃料用完,乙行驶到B地再返回A地时燃料用完,如图:
设AB=xkm,AC=ykm,根据题意得:
,
解得:.
∴乙在C地时加注行驶70km的燃料,则AB的最大长度是140km.
或者:设AC=ykm即可,从甲车的角度考虑问题,甲车给乙车注入燃料,要想最远,需满足以下两个条件:①注满乙车;②刚好够甲车从C回到A.从A到C,甲、乙两车都行驶了AC,即乙车行驶ykm,也即甲车注入燃料量可行驶ykm,注入后甲车剩余油量可行驶ykm(刚好返回A地),所以对于甲车,y+y+y=210,所以y=70.从乙车角度,从C出发是满燃料,所以AB为:105+70÷2=140(km).
故选:B.
3.利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式放置,再交换两木块的位置,按图②所示的方式放置.测量的数据如图,则桌子的高度等于( )
A.80cm B.75cm C.70cm D.65cm
【解答】解:设长方体木块长xcm、宽ycm,桌子的高为acm,
由题意得:,
两式相加得:2a=150,
解得:a=75,
故选:B.
4.某种高端品牌的家用电器,若按标价打八折销售该电器一件,则可获利润500元,其利润率为20%.现如果按同一标价打九折销售该电器一件,那么获得的纯利润为( )
A.562.5元 B.875元 C.550元 D.750元
【解答】解:设该商品的进价为x元,标价为y元,由题意得
,
解得:x=2500,y=3750.
则3750×0.9﹣2500=875(元).
故选:B.
5.甲、乙两人分别从相距40千米的两地同时出发,若同向而行,则5小时后,快者追上慢者;若相向而行,则2小时后,两人相遇,那么快者速度和慢者速度(单位:千米/小时)分别是( )
A.14和6 B.24和16 C.28和12 D.30和10
【解答】解:设快者速度和慢者速度分别是x,y,
则,
解得,
故选:A.
6.小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图(1);小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图(2)那样的正方形,中间还留下了一个洞,恰好是边长为3mm的小正方形,则每个小长方形的面积为( )
A.120mm2 B.135mm2 C.108mm2 D.96mm2
【解答】解:设每个长方形的长为xmm,宽为 ymm,由题意,
得,
解得:.
9×15=135(mm2).
故选:B.
7.一道来自课本的习题:
从甲地到乙地有一段上坡与一段平路.如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min.甲地到乙地全程是多少?
小红将这个实际问题转化为二元一次方程组问题,设未知数x,y,已经列出一个方程+=,则另一个方程正确的是( )
A.+= B.+= C.+= D.+=
【解答】解:设未知数x,y,已经列出一个方程+=,则另一个方程正确的是:+=.
故选:B.
8.《九章算术》第七卷“盈不足”中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”译为:“今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又差4钱.问人数、物价各多少?”根据所学知识,计算出人数、物价分别是( )
A.1,11 B.7,53 C.7,61 D.6,50
【解答】解:设有x人,物价为y,可得:,
解得:,
故选:B.
9.如图,在长方形ABCD中,放入六个形状大小相同的长方形,所标尺寸如图所示,则图中阴影部分面积为( )
A.44cm2 B.36cm2 C.96cm2 D.84cm2
【解答】解:设小长方形的长为xcm,宽为ycm,
依题意,得:,
解得:,
∴14×(6+2×2)﹣6×8×2=44(cm2).
故选:A.
二.填空题
10.一个自行车轮胎,若把它安装在前轮,则自行车行驶5000km后报废;若把它安装在后轮,则自行车行驶3000km后报废,行驶一定路程后可以交换前、后轮胎.如果交换前、后轮胎,要使一辆自行车的一对新轮胎同时报废,那么这辆车将能行驶 3750 km.
【解答】解:设每个新轮胎报废时的总磨损量为k,则安装在前轮的轮胎每行驶1km磨损量为,安装在后轮的轮胎每行驶1km的磨损量为.
又设一对新轮胎交换位置前走了xkm,交换位置后走了ykm.
分别以一个轮胎的总磨损量为等量关系列方程,有
两式相加,得,
则(千米).
故答案为:3750.
11.一个两位数的数字和为14,若调换个位数字与十位数字,新数比原数小36,则这个两位数是 95 .
【解答】解:设原来十位上数字为x,个位上的数字为y,
由题意得,,
解得:,
故这个两位数为95.
故答案为:95.
12.现有八个大小相同的长方形,可拼成如图1、2所示的图形,在拼图2时,中间留下了一个边长为2的小正方形,则每个小长方形的长是 10 .
【解答】解:设小长方形的长为x,宽为y,
根据题意得:,
解得:,
则每个小长方形的长是10;
故答案为:10.
13.新学期伊始,西大附中的学子们积极响应学校的“书香校园”活动,踊跃捐出自己喜爱的书籍,互相分享,让阅读成为一种习惯.据调查,某年级甲班、乙班共80人捐书,丙班有40人捐书,已知乙班人均捐书数量比甲班人均捐书数量多5本,而丙班的人均捐书数量是甲班人均捐书数量的一半,若该年级甲、乙、丙三班的人均捐书数量恰好是乙班人均捐书数量的,且各班人均捐书数量均为正整数,则甲、乙、丙三班共捐书 1080 本.
【解答】解:设甲班的人均捐书数量为x本,乙班的人均捐书数量为(x+5)本,丙班的人均捐书数量为本,
设甲班有y人,乙班有(80﹣y)人.
根据题意,得
xy+(x+5)(80﹣y)+ 40=
解得:y=
因为x,y均为正整数,故x=10或20,y=64或120,
因为120>80,
所以x=10,y=64,
共捐书10×64+15×16+5×40=1080.
答:甲、乙、丙三班共捐书1080本.
故答案为1080.
14.假设北碚万达广场地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为75%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.2019年元旦节期间,由于商场人数增多,早晨6点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过 小时车库恰好停满.
【解答】解:设1个进口1小时开进x辆车,1个出口1小时开出y辆,车位总数为a,由题意得
解得:,
则60%a÷(2×﹣)a=小时
答:从早晨6点开始经过小时车库恰好停满.
故答案为:.
15.如图,长为4a的长方形,沿图中虚线裁剪成四个形状大小完全相同的小长方形,那么每个小长方形的周长为 6a (用含a的代数式表示).
【解答】解:如图,,
解得.
所以2(x+y)=2(2a+a)=6a.
故答案是:6a.
16.我国明代数学读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托.如果1托为5尺,那么索长为 20 尺,竿子长为 15 尺.
【解答】解:设索长为x尺,竿子长为y尺,
根据题意得:,
解得:.
答:索长为20尺,竿子长为15尺.
故答案为:20;15.
17.一个两位数,十位数字比个位数字大3,若将十位数字和个位数交换位置,所得的新两位数比原两位数的多15,则这个两位数是 63 .
【解答】解:设这个两位数的十位数字为x,个位数字为y,由题意得
解得:
∴这个两位数为63.
故答案为:63.
18.一天,小民去问爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生呢,你若是我现在这么大,我已经是老寿星了,125岁了,哈哈!”请你写出小民爷爷到底是 70 岁.
【解答】解:设小民爷爷是x岁,小民是y岁,
依题意得:,
解得:.
故答案为:70.
三.解答题
19.根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高 2 cm,放入一个大球水面升高 3 cm;
(2)如果要使水面上升到50cm,应放入大球、小球各多少个?
【解答】解:(1)设一个小球使水面升高x厘米,由图意,得3x=32﹣26,解得x=2;
设一个大球使水面升高y厘米,由图意,得2y=32﹣26,解得:y=3.
所以,放入一个小球水面升高2cm,放入一个大球水面升高3cm;
(2)设应放入大球m个,小球n个.由题意,得
解得:,
答:如果要使水面上升到50cm,应放入大球4个,小球6个.
20.随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
【解答】解:(1)设打折前甲品牌粽子每盒x元,乙品牌粽子每盒y元,
根据题意得:,
解得:.
答:打折前甲品牌粽子每盒70元,乙品牌粽子每盒80元.
(2)80×70×(1﹣80%)+100×80×(1﹣75%)=3120(元).
答:打折后购买这批粽子比不打折节省了3120元.
21.某体育彩票经销商计划用45000元从省体彩中心购进彩票20扎,每扎1000张,已知体彩中心有A、B、C三种不同价格的彩票,进价分别是A彩票每张1.5元,B彩票每张2元,C彩票每张2.5元.
(1)若经销商同时购进两种不同型号的彩票20扎,用去45000元,请你设计进票方案;
(2)若销售A型彩票一张获手续费0.2元,B型彩票一张获手续费0.3元,C型彩票一张获手续费0.5元.在购进两种彩票的方案中,为使销售完时获得手续费最多,你选择哪种进票方案?
(3)若经销商准备用45000元同时购进A、B、C三种彩票20扎,请你设计进票方案.
【解答】解:(1)若设购进A种彩票x张,B种彩票y张,
根据题意得:x+y=1000×20;1.5x+2y=45000,
解得:x=﹣10000,y=30000,
∴x<0,不合题意;
若设购进A种彩票x张,C种彩票y张,
根据题意得:x+y=1000×20;1.5x+2.5y=45000,
解得:x=5000,y=15000,
若设购进B种彩票x张,C种彩票y张,
根据题意得:2x+2.5y=45000;x+y=1000×20.
解得:x=10000,y=10000,
综上所述,若经销商同时购进两种不同型号的彩票共有两种方案可行,
即A种彩票5扎,C种彩票15扎或B种彩票与C种彩票各10扎;
(2)若购进A种彩票5扎,C种彩票15扎,
销售完后获手续费为0.2×5000+0.5×15000=8500(元),
若购进B种彩票与C种彩票各10扎,
销售完后获手续费为0.3×10000+0.5×10000=8000(元),
∴为使销售完时获得手续最多选择的方案为A种彩票5扎,C种彩票15扎;
(3)若经销商准备用45000元同时购进A、B、C三种彩票20扎.
设购进A种彩票m扎,B种彩票n扎,C种彩票h扎.
由题意得:m+n+h=20;1.5×1000m+2×1000n+2.5×1000h=45000,即h=m+10,
∴n=﹣2m+10,
∵m、n都是正数
∴1≤m<5,
又m为整数共有4种进票方案,具体如下:
方案1:A种1扎,B种8扎,C种11扎;
方案2:A种2扎,B种6扎,C种12扎;
方案3:A种3扎,B种4扎,C种13扎;
方案4:A种4扎,B种2扎,C种14扎.
22.小林在某商店购买商品A,B共三次,只有其中一次购买时,商品A,B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如表所示,
购买商品A的数量/个 购买商品B的数量/个 购买总费用/元
第一次购物 6 5 1140
第二次购物 3 7 1110
第三次购物 9 8 1062
(1)在这三次购物中,第 三 次购物打了折扣;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
【解答】解:(1)小林以折扣价购买商品A、B是第三次购物.
故答案为:三;
(2)设商品A的标价为x元,商品B的标价为y元,
根据题意,得,
解得:.
答:商品A的标价为90元,商品B的标价为120元;
(3)设商店是打a折出售这两种商品,
由题意得,(9×90+8×120)×=1062,
解得:a=6.
答:商店是打6折出售这两种商品的.
一.选择题
1.利用两块相同的长方体木块测量一张桌子的高度.首先按图1方式放置,再交换两木块的位置,按图2方式放置.测量的数据如图,则桌子的高度是( )
A.73cm B.74cm C.75cm D.76cm
2.同型号的甲、乙两辆车加满气体燃料后均可行驶210km,它们各自单独行驶并返回的最远距离是105km.现在它们都从A地出发,行驶途中停下来从甲车的气体燃料桶抽一些气体燃料注入乙车的气体燃料桶,然后甲车再行驶返回A地,而乙车继续行驶,到B地后再行驶返回A地.则B地最远可距离A地( )
A.120km B.140km C.160km D.180km
3.利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式放置,再交换两木块的位置,按图②所示的方式放置.测量的数据如图,则桌子的高度等于( )
A.80cm B.75cm C.70cm D.65cm
4.某种高端品牌的家用电器,若按标价打八折销售该电器一件,则可获利润500元,其利润率为20%.现如果按同一标价打九折销售该电器一件,那么获得的纯利润为( )
A.562.5元 B.875元 C.550元 D.750元
5.甲、乙两人分别从相距40千米的两地同时出发,若同向而行,则5小时后,快者追上慢者;若相向而行,则2小时后,两人相遇,那么快者速度和慢者速度(单位:千米/小时)分别是( )
A.14和6 B.24和16 C.28和12 D.30和10
6.小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图(1);小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图(2)那样的正方形,中间还留下了一个洞,恰好是边长为3mm的小正方形,则每个小长方形的面积为( )
A.120mm2 B.135mm2 C.108mm2 D.96mm2
7.一道来自课本的习题:
从甲地到乙地有一段上坡与一段平路.如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min.甲地到乙地全程是多少?
小红将这个实际问题转化为二元一次方程组问题,设未知数x,y,已经列出一个方程+=,则另一个方程正确的是( )
A.+= B.+= C.+= D.+=
8.《九章算术》第七卷“盈不足”中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”译为:“今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又差4钱.问人数、物价各多少?”根据所学知识,计算出人数、物价分别是( )
A.1,11 B.7,53 C.7,61 D.6,50
9.如图,在长方形ABCD中,放入六个形状大小相同的长方形,所标尺寸如图所示,则图中阴影部分面积为( )
A.44cm2 B.36cm2 C.96cm2 D.84cm2
二.填空题
10.一个自行车轮胎,若把它安装在前轮,则自行车行驶5000km后报废;若把它安装在后轮,则自行车行驶3000km后报废,行驶一定路程后可以交换前、后轮胎.如果交换前、后轮胎,要使一辆自行车的一对新轮胎同时报废,那么这辆车将能行驶 km.
11.一个两位数的数字和为14,若调换个位数字与十位数字,新数比原数小36,则这个两位数是 .
12.现有八个大小相同的长方形,可拼成如图1、2所示的图形,在拼图2时,中间留下了一个边长为2的小正方形,则每个小长方形的长是 .
13.新学期伊始,西大附中的学子们积极响应学校的“书香校园”活动,踊跃捐出自己喜爱的书籍,互相分享,让阅读成为一种习惯.据调查,某年级甲班、乙班共80人捐书,丙班有40人捐书,已知乙班人均捐书数量比甲班人均捐书数量多5本,而丙班的人均捐书数量是甲班人均捐书数量的一半,若该年级甲、乙、丙三班的人均捐书数量恰好是乙班人均捐书数量的,且各班人均捐书数量均为正整数,则甲、乙、丙三班共捐书 本.
14.假设北碚万达广场地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为75%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.2019年元旦节期间,由于商场人数增多,早晨6点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过 小时车库恰好停满.
15.如图,长为4a的长方形,沿图中虚线裁剪成四个形状大小完全相同的小长方形,那么每个小长方形的周长为 (用含a的代数式表示).
16.我国明代数学读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托.如果1托为5尺,那么索长为 尺,竿子长为 尺.
17.一个两位数,十位数字比个位数字大3,若将十位数字和个位数交换位置,所得的新两位数比原两位数的多15,则这个两位数是 .
18.一天,小民去问爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生呢,你若是我现在这么大,我已经是老寿星了,125岁了,哈哈!”请你写出小民爷爷到底是 岁.
三.解答题
19.根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高 cm,放入一个大球水面升高 cm;
(2)如果要使水面上升到50cm,应放入大球、小球各多少个?
20.随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
21.某体育彩票经销商计划用45000元从省体彩中心购进彩票20扎,每扎1000张,已知体彩中心有A、B、C三种不同价格的彩票,进价分别是A彩票每张1.5元,B彩票每张2元,C彩票每张2.5元.
(1)若经销商同时购进两种不同型号的彩票20扎,用去45000元,请你设计进票方案;
(2)若销售A型彩票一张获手续费0.2元,B型彩票一张获手续费0.3元,C型彩票一张获手续费0.5元.在购进两种彩票的方案中,为使销售完时获得手续费最多,你选择哪种进票方案?
(3)若经销商准备用45000元同时购进A、B、C三种彩票20扎,请你设计进票方案.
22.小林在某商店购买商品A,B共三次,只有其中一次购买时,商品A,B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如表所示,
购买商品A的数量/个 购买商品B的数量/个 购买总费用/元
第一次购物 6 5 1140
第二次购物 3 7 1110
第三次购物 9 8 1062
(1)在这三次购物中,第 次购物打了折扣;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
二元一次方程组的应用题
参考答案与试题解析
一.选择题
1.利用两块相同的长方体木块测量一张桌子的高度.首先按图1方式放置,再交换两木块的位置,按图2方式放置.测量的数据如图,则桌子的高度是( )
A.73cm B.74cm C.75cm D.76cm
【解答】解:设长方体长xcm,宽ycm,桌子的高为acm,由题意,得
,
解得:2a=152,
∴a=76.
故选:D.
2.同型号的甲、乙两辆车加满气体燃料后均可行驶210km,它们各自单独行驶并返回的最远距离是105km.现在它们都从A地出发,行驶途中停下来从甲车的气体燃料桶抽一些气体燃料注入乙车的气体燃料桶,然后甲车再行驶返回A地,而乙车继续行驶,到B地后再行驶返回A地.则B地最远可距离A地( )
A.120km B.140km C.160km D.180km
【解答】解:设甲行驶到C地时返回,到达A地燃料用完,乙行驶到B地再返回A地时燃料用完,如图:
设AB=xkm,AC=ykm,根据题意得:
,
解得:.
∴乙在C地时加注行驶70km的燃料,则AB的最大长度是140km.
或者:设AC=ykm即可,从甲车的角度考虑问题,甲车给乙车注入燃料,要想最远,需满足以下两个条件:①注满乙车;②刚好够甲车从C回到A.从A到C,甲、乙两车都行驶了AC,即乙车行驶ykm,也即甲车注入燃料量可行驶ykm,注入后甲车剩余油量可行驶ykm(刚好返回A地),所以对于甲车,y+y+y=210,所以y=70.从乙车角度,从C出发是满燃料,所以AB为:105+70÷2=140(km).
故选:B.
3.利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式放置,再交换两木块的位置,按图②所示的方式放置.测量的数据如图,则桌子的高度等于( )
A.80cm B.75cm C.70cm D.65cm
【解答】解:设长方体木块长xcm、宽ycm,桌子的高为acm,
由题意得:,
两式相加得:2a=150,
解得:a=75,
故选:B.
4.某种高端品牌的家用电器,若按标价打八折销售该电器一件,则可获利润500元,其利润率为20%.现如果按同一标价打九折销售该电器一件,那么获得的纯利润为( )
A.562.5元 B.875元 C.550元 D.750元
【解答】解:设该商品的进价为x元,标价为y元,由题意得
,
解得:x=2500,y=3750.
则3750×0.9﹣2500=875(元).
故选:B.
5.甲、乙两人分别从相距40千米的两地同时出发,若同向而行,则5小时后,快者追上慢者;若相向而行,则2小时后,两人相遇,那么快者速度和慢者速度(单位:千米/小时)分别是( )
A.14和6 B.24和16 C.28和12 D.30和10
【解答】解:设快者速度和慢者速度分别是x,y,
则,
解得,
故选:A.
6.小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图(1);小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图(2)那样的正方形,中间还留下了一个洞,恰好是边长为3mm的小正方形,则每个小长方形的面积为( )
A.120mm2 B.135mm2 C.108mm2 D.96mm2
【解答】解:设每个长方形的长为xmm,宽为 ymm,由题意,
得,
解得:.
9×15=135(mm2).
故选:B.
7.一道来自课本的习题:
从甲地到乙地有一段上坡与一段平路.如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min.甲地到乙地全程是多少?
小红将这个实际问题转化为二元一次方程组问题,设未知数x,y,已经列出一个方程+=,则另一个方程正确的是( )
A.+= B.+= C.+= D.+=
【解答】解:设未知数x,y,已经列出一个方程+=,则另一个方程正确的是:+=.
故选:B.
8.《九章算术》第七卷“盈不足”中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”译为:“今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又差4钱.问人数、物价各多少?”根据所学知识,计算出人数、物价分别是( )
A.1,11 B.7,53 C.7,61 D.6,50
【解答】解:设有x人,物价为y,可得:,
解得:,
故选:B.
9.如图,在长方形ABCD中,放入六个形状大小相同的长方形,所标尺寸如图所示,则图中阴影部分面积为( )
A.44cm2 B.36cm2 C.96cm2 D.84cm2
【解答】解:设小长方形的长为xcm,宽为ycm,
依题意,得:,
解得:,
∴14×(6+2×2)﹣6×8×2=44(cm2).
故选:A.
二.填空题
10.一个自行车轮胎,若把它安装在前轮,则自行车行驶5000km后报废;若把它安装在后轮,则自行车行驶3000km后报废,行驶一定路程后可以交换前、后轮胎.如果交换前、后轮胎,要使一辆自行车的一对新轮胎同时报废,那么这辆车将能行驶 3750 km.
【解答】解:设每个新轮胎报废时的总磨损量为k,则安装在前轮的轮胎每行驶1km磨损量为,安装在后轮的轮胎每行驶1km的磨损量为.
又设一对新轮胎交换位置前走了xkm,交换位置后走了ykm.
分别以一个轮胎的总磨损量为等量关系列方程,有
两式相加,得,
则(千米).
故答案为:3750.
11.一个两位数的数字和为14,若调换个位数字与十位数字,新数比原数小36,则这个两位数是 95 .
【解答】解:设原来十位上数字为x,个位上的数字为y,
由题意得,,
解得:,
故这个两位数为95.
故答案为:95.
12.现有八个大小相同的长方形,可拼成如图1、2所示的图形,在拼图2时,中间留下了一个边长为2的小正方形,则每个小长方形的长是 10 .
【解答】解:设小长方形的长为x,宽为y,
根据题意得:,
解得:,
则每个小长方形的长是10;
故答案为:10.
13.新学期伊始,西大附中的学子们积极响应学校的“书香校园”活动,踊跃捐出自己喜爱的书籍,互相分享,让阅读成为一种习惯.据调查,某年级甲班、乙班共80人捐书,丙班有40人捐书,已知乙班人均捐书数量比甲班人均捐书数量多5本,而丙班的人均捐书数量是甲班人均捐书数量的一半,若该年级甲、乙、丙三班的人均捐书数量恰好是乙班人均捐书数量的,且各班人均捐书数量均为正整数,则甲、乙、丙三班共捐书 1080 本.
【解答】解:设甲班的人均捐书数量为x本,乙班的人均捐书数量为(x+5)本,丙班的人均捐书数量为本,
设甲班有y人,乙班有(80﹣y)人.
根据题意,得
xy+(x+5)(80﹣y)+ 40=
解得:y=
因为x,y均为正整数,故x=10或20,y=64或120,
因为120>80,
所以x=10,y=64,
共捐书10×64+15×16+5×40=1080.
答:甲、乙、丙三班共捐书1080本.
故答案为1080.
14.假设北碚万达广场地下停车场有5个出入口,每天早晨6点开始对外停车且此时车位空置率为75%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,8小时车库恰好停满;如果开放3个进口和2个出口,2小时车库恰好停满.2019年元旦节期间,由于商场人数增多,早晨6点时的车位空置率变为60%,又因为车库改造,只能开放2个进口和1个出口,则从早晨6点开始经过 小时车库恰好停满.
【解答】解:设1个进口1小时开进x辆车,1个出口1小时开出y辆,车位总数为a,由题意得
解得:,
则60%a÷(2×﹣)a=小时
答:从早晨6点开始经过小时车库恰好停满.
故答案为:.
15.如图,长为4a的长方形,沿图中虚线裁剪成四个形状大小完全相同的小长方形,那么每个小长方形的周长为 6a (用含a的代数式表示).
【解答】解:如图,,
解得.
所以2(x+y)=2(2a+a)=6a.
故答案是:6a.
16.我国明代数学读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托.如果1托为5尺,那么索长为 20 尺,竿子长为 15 尺.
【解答】解:设索长为x尺,竿子长为y尺,
根据题意得:,
解得:.
答:索长为20尺,竿子长为15尺.
故答案为:20;15.
17.一个两位数,十位数字比个位数字大3,若将十位数字和个位数交换位置,所得的新两位数比原两位数的多15,则这个两位数是 63 .
【解答】解:设这个两位数的十位数字为x,个位数字为y,由题意得
解得:
∴这个两位数为63.
故答案为:63.
18.一天,小民去问爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生呢,你若是我现在这么大,我已经是老寿星了,125岁了,哈哈!”请你写出小民爷爷到底是 70 岁.
【解答】解:设小民爷爷是x岁,小民是y岁,
依题意得:,
解得:.
故答案为:70.
三.解答题
19.根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高 2 cm,放入一个大球水面升高 3 cm;
(2)如果要使水面上升到50cm,应放入大球、小球各多少个?
【解答】解:(1)设一个小球使水面升高x厘米,由图意,得3x=32﹣26,解得x=2;
设一个大球使水面升高y厘米,由图意,得2y=32﹣26,解得:y=3.
所以,放入一个小球水面升高2cm,放入一个大球水面升高3cm;
(2)设应放入大球m个,小球n个.由题意,得
解得:,
答:如果要使水面上升到50cm,应放入大球4个,小球6个.
20.随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
【解答】解:(1)设打折前甲品牌粽子每盒x元,乙品牌粽子每盒y元,
根据题意得:,
解得:.
答:打折前甲品牌粽子每盒70元,乙品牌粽子每盒80元.
(2)80×70×(1﹣80%)+100×80×(1﹣75%)=3120(元).
答:打折后购买这批粽子比不打折节省了3120元.
21.某体育彩票经销商计划用45000元从省体彩中心购进彩票20扎,每扎1000张,已知体彩中心有A、B、C三种不同价格的彩票,进价分别是A彩票每张1.5元,B彩票每张2元,C彩票每张2.5元.
(1)若经销商同时购进两种不同型号的彩票20扎,用去45000元,请你设计进票方案;
(2)若销售A型彩票一张获手续费0.2元,B型彩票一张获手续费0.3元,C型彩票一张获手续费0.5元.在购进两种彩票的方案中,为使销售完时获得手续费最多,你选择哪种进票方案?
(3)若经销商准备用45000元同时购进A、B、C三种彩票20扎,请你设计进票方案.
【解答】解:(1)若设购进A种彩票x张,B种彩票y张,
根据题意得:x+y=1000×20;1.5x+2y=45000,
解得:x=﹣10000,y=30000,
∴x<0,不合题意;
若设购进A种彩票x张,C种彩票y张,
根据题意得:x+y=1000×20;1.5x+2.5y=45000,
解得:x=5000,y=15000,
若设购进B种彩票x张,C种彩票y张,
根据题意得:2x+2.5y=45000;x+y=1000×20.
解得:x=10000,y=10000,
综上所述,若经销商同时购进两种不同型号的彩票共有两种方案可行,
即A种彩票5扎,C种彩票15扎或B种彩票与C种彩票各10扎;
(2)若购进A种彩票5扎,C种彩票15扎,
销售完后获手续费为0.2×5000+0.5×15000=8500(元),
若购进B种彩票与C种彩票各10扎,
销售完后获手续费为0.3×10000+0.5×10000=8000(元),
∴为使销售完时获得手续最多选择的方案为A种彩票5扎,C种彩票15扎;
(3)若经销商准备用45000元同时购进A、B、C三种彩票20扎.
设购进A种彩票m扎,B种彩票n扎,C种彩票h扎.
由题意得:m+n+h=20;1.5×1000m+2×1000n+2.5×1000h=45000,即h=m+10,
∴n=﹣2m+10,
∵m、n都是正数
∴1≤m<5,
又m为整数共有4种进票方案,具体如下:
方案1:A种1扎,B种8扎,C种11扎;
方案2:A种2扎,B种6扎,C种12扎;
方案3:A种3扎,B种4扎,C种13扎;
方案4:A种4扎,B种2扎,C种14扎.
22.小林在某商店购买商品A,B共三次,只有其中一次购买时,商品A,B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如表所示,
购买商品A的数量/个 购买商品B的数量/个 购买总费用/元
第一次购物 6 5 1140
第二次购物 3 7 1110
第三次购物 9 8 1062
(1)在这三次购物中,第 三 次购物打了折扣;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
【解答】解:(1)小林以折扣价购买商品A、B是第三次购物.
故答案为:三;
(2)设商品A的标价为x元,商品B的标价为y元,
根据题意,得,
解得:.
答:商品A的标价为90元,商品B的标价为120元;
(3)设商店是打a折出售这两种商品,
由题意得,(9×90+8×120)×=1062,
解得:a=6.
答:商店是打6折出售这两种商品的.
