第29章投影与视图单元测试 (含解析)人教版九年级数学下册
文档属性
| 名称 | 第29章投影与视图单元测试 (含解析)人教版九年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 1010.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-29 21:01:46 | ||
图片预览



文档简介
人教版九下 第29章 投影与视图 单元测试
一、选择题(共10小题)
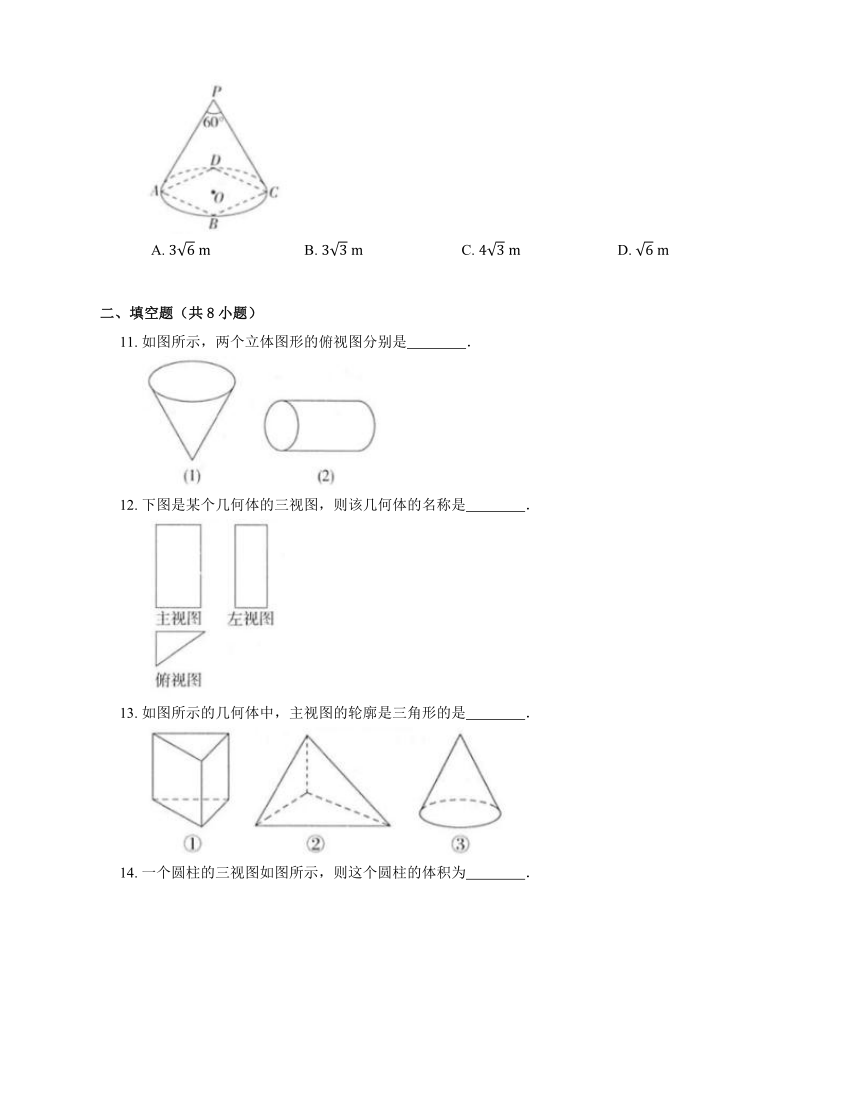
1. 我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时,两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,它的俯视图是
A. B.
C. D.
2. 如图所示的主视图和俯视图,其对应的几何体可以是
A. B.
C. D.
3. 睹影知竿,指看竹竿的影子,便知道竹竿的曲直长短.其中形成“影”的光源是
A. 油灯 B. 蜡烛 C. 太阳 D. 纱灯
4. 在某节目中,《海市蜃楼》是一个关于字母的中心投影的比赛项目:通过观察投影猜字母.若投影中有一段弧,则对应的字母可能是
A. B. C. D.
5. 如图是由 个相同的小立方块搭成的几何体,在这个几何体的三视图中,是轴对称图形的为
A. 主视图 B. 左视图
C. 俯视图 D. 主视图和左视图
6. 小阳和小明两人从远处沿直线走到路灯下,他们规定:小阳在前,小明在后,两人之间的距离始终与小阳的影长相等.在这种情况下,他们两人之间的距离
A. 始终不变 B. 越来越远 C. 时近时远 D. 越来越近
7. 下图是由若干个相同的小正方体搭成的一个几何体的主视图和左视图,则所需的小正方体的个数最少是
A. B. C. D.
8. 下列说法正确的是
A. 三角形的正投影一定是三角形 B. 长方形的正投影一定是长方形
C. 球的正投影一定是圆 D. 圆锥的正投影一定是三角形
9. 下图①是一个棱长为 的三棱锥,它的三视图如图②所示,则在它的三视图中,边长为 的线段条数为
A. B. C. D.
10. 如图,某剧院舞台上的照明灯 射出的光线形成“锥体”,该“锥体”截面图的“锥角”是 ,已知舞台 是边长为 的正方形,要使灯光恰好能照射到整个舞台,则照明灯 悬挂的高度是
A. B. C. D.
二、填空题(共8小题)
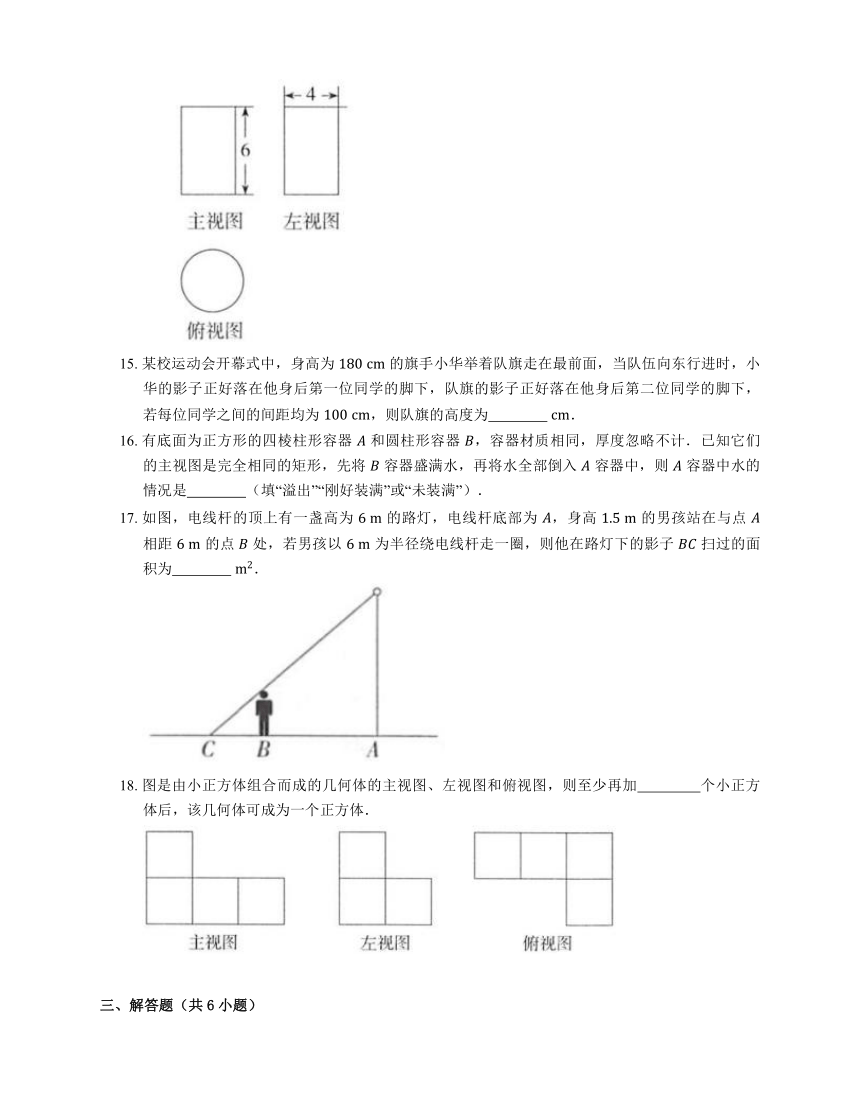
11. 如图所示,两个立体图形的俯视图分别是 .
12. 下图是某个几何体的三视图,则该几何体的名称是 .
13. 如图所示的几何体中,主视图的轮廓是三角形的是 .
14. 一个圆柱的三视图如图所示,则这个圆柱的体积为 .
15. 某校运动会开幕式中,身高为 的旗手小华举着队旗走在最前面,当队伍向东行进时,小华的影子正好落在他身后第一位同学的脚下,队旗的影子正好落在他身后第二位同学的脚下,若每位同学之间的间距均为 ,则队旗的高度为 .
16. 有底面为正方形的四棱柱形容器 和圆柱形容器 ,容器材质相同,厚度忽略不计.已知它们的主视图是完全相同的矩形,先将 容器盛满水,再将水全部倒入 容器中,则 容器中水的情况是 (填“溢出”“刚好装满”或“未装满”).
17. 如图,电线杆的顶上有一盏高为 的路灯,电线杆底部为 ,身高 的男孩站在与点 相距 的点 处,若男孩以 为半径绕电线杆走一圈,则他在路灯下的影子 扫过的面积为 .
18. 图是由小正方体组合而成的几何体的主视图、左视图和俯视图,则至少再加 个小正方体后,该几何体可成为一个正方体.
三、解答题(共6小题)
19. 小红想利用阳光下的影长测量学校旗杆 的高度.如图,某一时刻她在地面上竖直立了一个 长的标杆 ,测得其影长 .
(1)请在图中画出此时旗杆 在阳光下的投影 ;
(2)如果 ,求旗杆 的高.
20. 分别画出如图所示的几何体的主视图、左视图、俯视图.
21. 如图是一个几何体的三视图.
(1)写出这个几何体的名称: ;
(2)画出它的一种表面展开图;
(3)求这个几何体的侧面积.
22. 由一些大小相同,棱长为 的小正方体搭成的几何体的俯视图如下图所示,数字表示该位置上的小正方体个数.
(1)请在下图中画出它的主视图和左视图;
(2)给这个几何体喷上颜色(底面不喷色),需要喷色的面积为 .
(3)在不改变主视图和俯视图的情况下,最多可添加 个小正方体.
23. 如图,某光源下有三根杆子,甲杆 的影子为 ,乙杆 的影子一部分落在地面上(),一部分落在斜坡 上().
(1)请在图中画出形成影子的光线,确定光源所在的位置 ,并画出丙杆 在地面上的影子;
(2)在()的结论下,若过点 的光线 ,斜坡与地面夹角为 ,,,请求出乙杆 的高度.(结果保留根号)
24. 如图所示,有 张除了正面图案不同,其余都相同的卡片.
(1)在四张卡片正面所示的立体图形中,主视图是矩形的有 ;(填字母序号)
(2)将这四张卡片背面朝上洗匀,从中随机抽出一张后放回,洗匀后再随机抽出一张.求两次抽出的卡片正面所示的立体图形中,主视图都是矩形的概率;
(3)按照图中卡片正面图案的样子任选两个制作成模型,并把这两个模型上下放置,请画出组合后所得一种几何体的三视图.
答案
1. A
【解析】横向圆柱的俯视图是正方形,纵向圆柱的俯视图是圆,正方体的俯视图是正方形,结合题图可知几何体俯视图中两正方形横向并排,且圆在右侧正方形内.
2. D
【解析】画出选项中各几何体的主视图和俯视图(图略),可知D符合题意,故选D.
3. C
【解析】在太阳光下形成的是平行投影,影长与物体高度成正比,根据影子的长短可知竹竿的长短;在灯光下形成的是中心投影,竹竿离光源的远近不同时,影长不同,不能根据影子的长短判断竹竿的长短.
4. B
【解析】字母“”中的弧在中心投影中可得到一段弧,而字母“”“”“”都是直线型,在中心投影中不可能得到弧.
5. D
【解析】该几何体的三视图如图所示,主视图和左视图都是轴对称图形.
6. D
【解析】因为在小阳和小明两人从远处沿直线走到路灯下这一过程中,与光源的距离是由远到近的,
所以他们在地上的影子会变短,所以他们两人之间的距离越来越近.故选D.
7. C
【解析】根据左视图与主视图可知该几何体共有 层,底层最少有 个小正方体,第二层最少有 个小正方体,第三层最少有 个小正方体,画出此时的俯视图如图(俯视图中数字表示相应位置处小正方体的个数),
则所需的小正方体的个数最少是 .
8. C
【解析】选项A,三角形的正投影可能是三角形、线段,故A错误;
选项B,长方形的正投影可能是长方形、平行四边形、线段,故B错误;
选项C,球的正投影一定是圆,故C正确;
选项D,圆锥的正投影有可能是圆,故D错误.故选C.
9. B
【解析】如图,
由题意知,主视图中仅线段 的长为 ,左视图中仅线段 的长为 ,俯视图中仅线段 ,, 的长为 ,所以三视图中,长度为 的线段有 条.
10. A
【解析】如图,连接 ,,易知 在 上,.
,,
,
,
四边形 是边长为 的正方形,
,
,
,
.故选A.
11. 中心有一点的圆,矩形
【解析】俯视图如图所示,
即题中两个立体图形的俯视图分别是中心有一点的圆和矩形.
12. 三棱柱
【解析】由主视图和左视图为矩形可得该几何体是柱体,由俯视图是三角形可得该几何体是三棱柱.
13. ②③
【解析】①的主视图的轮廓是矩形;
②的主视图的轮廓是三角形,
③的主视图的轮廓是等腰三角形,
故答案是②③.
14.
【解析】由三视图可得该圆柱的高为 ,底面直径为 ,则这个圆柱的体积为 .
15.
【解析】由题意知,小华的影长为 ,队旗的影长为 ,设队旗的高度为 ,则 ,解得 ,所以队旗的高度为 .
16. 未装满
【解析】设容器 的底面边长为 ,高为 ,则容器 的体积 ,
容器 , 的主视图完全相同,
容器 的高为 ,底面直径为 ,
容器 的体积 ,
,
容器 的体积小于容器 的体积,
将 容器盛满水,再将水全部倒入 容器中,结果是 容器未装满.
17.
【解析】如图,
,
,
,即 ,解得 ,
,
男孩以 为半径绕电线杆走一圈,
他在路灯下的影子 扫过的面积为 .
18.
【解析】观察三视图,可知这个几何体各个位置上的小正方体的个数,在俯视图上标出如图所示,
则由题意可知最小可以组成 的正方体,即组成的正方体共有 个小正方体,,
所以至少再加 个小正方体后,才能组成一个正方体.
19. (1) 如图,连接 ,作 交 于 ,
则 即为所求.
(2) ,
.
而 ,
,
,即 ,
.
答:旗杆 的高为 .
20. 如图所示.
21. (1) 三棱柱
(2) 表面展开图如图所示(答案不唯一).
(3) ,
这个几何体的侧面积为 .
22. (1) 该几何体的主视图和左视图如图所示.
(2)
【解析】给这个几何体喷上颜色(底面不喷色),需要喷色的面有 个,所以喷色的面积为 .
(3)
【解析】在俯视图中标数字“”的正方形的位置上再添加 个小正方体,不会改变主视图和俯视图.
23. (1) 光线及光源所在的位置 如图,
即为 在地面的影子.
(2) 分别延长 , 交于点 ,则 ,,
,
又 ,
,
,
在 中,,
,
乙杆 的高度为 .
24. (1) ,
【解析】球的主视图为圆,长方体的主视图是矩形,圆锥的主视图为等腰三角形,圆柱的主视图为矩形,故填 ,.
(2) 列表如下:
由上表可知,共有 种等可能的结果,其中两次抽出的卡片正面所示立体图形的主视图都是矩形的有 种,分别是 ,,,,所以两次抽出的卡片正面所示立体图形的主视图都是矩形的概率为 ,即 .
(3) 答案不唯一,如选圆柱和圆锥组合,画三视图如下.
一、选择题(共10小题)
1. 我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时,两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型,它的俯视图是
A. B.
C. D.
2. 如图所示的主视图和俯视图,其对应的几何体可以是
A. B.
C. D.
3. 睹影知竿,指看竹竿的影子,便知道竹竿的曲直长短.其中形成“影”的光源是
A. 油灯 B. 蜡烛 C. 太阳 D. 纱灯
4. 在某节目中,《海市蜃楼》是一个关于字母的中心投影的比赛项目:通过观察投影猜字母.若投影中有一段弧,则对应的字母可能是
A. B. C. D.
5. 如图是由 个相同的小立方块搭成的几何体,在这个几何体的三视图中,是轴对称图形的为
A. 主视图 B. 左视图
C. 俯视图 D. 主视图和左视图
6. 小阳和小明两人从远处沿直线走到路灯下,他们规定:小阳在前,小明在后,两人之间的距离始终与小阳的影长相等.在这种情况下,他们两人之间的距离
A. 始终不变 B. 越来越远 C. 时近时远 D. 越来越近
7. 下图是由若干个相同的小正方体搭成的一个几何体的主视图和左视图,则所需的小正方体的个数最少是
A. B. C. D.
8. 下列说法正确的是
A. 三角形的正投影一定是三角形 B. 长方形的正投影一定是长方形
C. 球的正投影一定是圆 D. 圆锥的正投影一定是三角形
9. 下图①是一个棱长为 的三棱锥,它的三视图如图②所示,则在它的三视图中,边长为 的线段条数为
A. B. C. D.
10. 如图,某剧院舞台上的照明灯 射出的光线形成“锥体”,该“锥体”截面图的“锥角”是 ,已知舞台 是边长为 的正方形,要使灯光恰好能照射到整个舞台,则照明灯 悬挂的高度是
A. B. C. D.
二、填空题(共8小题)
11. 如图所示,两个立体图形的俯视图分别是 .
12. 下图是某个几何体的三视图,则该几何体的名称是 .
13. 如图所示的几何体中,主视图的轮廓是三角形的是 .
14. 一个圆柱的三视图如图所示,则这个圆柱的体积为 .
15. 某校运动会开幕式中,身高为 的旗手小华举着队旗走在最前面,当队伍向东行进时,小华的影子正好落在他身后第一位同学的脚下,队旗的影子正好落在他身后第二位同学的脚下,若每位同学之间的间距均为 ,则队旗的高度为 .
16. 有底面为正方形的四棱柱形容器 和圆柱形容器 ,容器材质相同,厚度忽略不计.已知它们的主视图是完全相同的矩形,先将 容器盛满水,再将水全部倒入 容器中,则 容器中水的情况是 (填“溢出”“刚好装满”或“未装满”).
17. 如图,电线杆的顶上有一盏高为 的路灯,电线杆底部为 ,身高 的男孩站在与点 相距 的点 处,若男孩以 为半径绕电线杆走一圈,则他在路灯下的影子 扫过的面积为 .
18. 图是由小正方体组合而成的几何体的主视图、左视图和俯视图,则至少再加 个小正方体后,该几何体可成为一个正方体.
三、解答题(共6小题)
19. 小红想利用阳光下的影长测量学校旗杆 的高度.如图,某一时刻她在地面上竖直立了一个 长的标杆 ,测得其影长 .
(1)请在图中画出此时旗杆 在阳光下的投影 ;
(2)如果 ,求旗杆 的高.
20. 分别画出如图所示的几何体的主视图、左视图、俯视图.
21. 如图是一个几何体的三视图.
(1)写出这个几何体的名称: ;
(2)画出它的一种表面展开图;
(3)求这个几何体的侧面积.
22. 由一些大小相同,棱长为 的小正方体搭成的几何体的俯视图如下图所示,数字表示该位置上的小正方体个数.
(1)请在下图中画出它的主视图和左视图;
(2)给这个几何体喷上颜色(底面不喷色),需要喷色的面积为 .
(3)在不改变主视图和俯视图的情况下,最多可添加 个小正方体.
23. 如图,某光源下有三根杆子,甲杆 的影子为 ,乙杆 的影子一部分落在地面上(),一部分落在斜坡 上().
(1)请在图中画出形成影子的光线,确定光源所在的位置 ,并画出丙杆 在地面上的影子;
(2)在()的结论下,若过点 的光线 ,斜坡与地面夹角为 ,,,请求出乙杆 的高度.(结果保留根号)
24. 如图所示,有 张除了正面图案不同,其余都相同的卡片.
(1)在四张卡片正面所示的立体图形中,主视图是矩形的有 ;(填字母序号)
(2)将这四张卡片背面朝上洗匀,从中随机抽出一张后放回,洗匀后再随机抽出一张.求两次抽出的卡片正面所示的立体图形中,主视图都是矩形的概率;
(3)按照图中卡片正面图案的样子任选两个制作成模型,并把这两个模型上下放置,请画出组合后所得一种几何体的三视图.
答案
1. A
【解析】横向圆柱的俯视图是正方形,纵向圆柱的俯视图是圆,正方体的俯视图是正方形,结合题图可知几何体俯视图中两正方形横向并排,且圆在右侧正方形内.
2. D
【解析】画出选项中各几何体的主视图和俯视图(图略),可知D符合题意,故选D.
3. C
【解析】在太阳光下形成的是平行投影,影长与物体高度成正比,根据影子的长短可知竹竿的长短;在灯光下形成的是中心投影,竹竿离光源的远近不同时,影长不同,不能根据影子的长短判断竹竿的长短.
4. B
【解析】字母“”中的弧在中心投影中可得到一段弧,而字母“”“”“”都是直线型,在中心投影中不可能得到弧.
5. D
【解析】该几何体的三视图如图所示,主视图和左视图都是轴对称图形.
6. D
【解析】因为在小阳和小明两人从远处沿直线走到路灯下这一过程中,与光源的距离是由远到近的,
所以他们在地上的影子会变短,所以他们两人之间的距离越来越近.故选D.
7. C
【解析】根据左视图与主视图可知该几何体共有 层,底层最少有 个小正方体,第二层最少有 个小正方体,第三层最少有 个小正方体,画出此时的俯视图如图(俯视图中数字表示相应位置处小正方体的个数),
则所需的小正方体的个数最少是 .
8. C
【解析】选项A,三角形的正投影可能是三角形、线段,故A错误;
选项B,长方形的正投影可能是长方形、平行四边形、线段,故B错误;
选项C,球的正投影一定是圆,故C正确;
选项D,圆锥的正投影有可能是圆,故D错误.故选C.
9. B
【解析】如图,
由题意知,主视图中仅线段 的长为 ,左视图中仅线段 的长为 ,俯视图中仅线段 ,, 的长为 ,所以三视图中,长度为 的线段有 条.
10. A
【解析】如图,连接 ,,易知 在 上,.
,,
,
,
四边形 是边长为 的正方形,
,
,
,
.故选A.
11. 中心有一点的圆,矩形
【解析】俯视图如图所示,
即题中两个立体图形的俯视图分别是中心有一点的圆和矩形.
12. 三棱柱
【解析】由主视图和左视图为矩形可得该几何体是柱体,由俯视图是三角形可得该几何体是三棱柱.
13. ②③
【解析】①的主视图的轮廓是矩形;
②的主视图的轮廓是三角形,
③的主视图的轮廓是等腰三角形,
故答案是②③.
14.
【解析】由三视图可得该圆柱的高为 ,底面直径为 ,则这个圆柱的体积为 .
15.
【解析】由题意知,小华的影长为 ,队旗的影长为 ,设队旗的高度为 ,则 ,解得 ,所以队旗的高度为 .
16. 未装满
【解析】设容器 的底面边长为 ,高为 ,则容器 的体积 ,
容器 , 的主视图完全相同,
容器 的高为 ,底面直径为 ,
容器 的体积 ,
,
容器 的体积小于容器 的体积,
将 容器盛满水,再将水全部倒入 容器中,结果是 容器未装满.
17.
【解析】如图,
,
,
,即 ,解得 ,
,
男孩以 为半径绕电线杆走一圈,
他在路灯下的影子 扫过的面积为 .
18.
【解析】观察三视图,可知这个几何体各个位置上的小正方体的个数,在俯视图上标出如图所示,
则由题意可知最小可以组成 的正方体,即组成的正方体共有 个小正方体,,
所以至少再加 个小正方体后,才能组成一个正方体.
19. (1) 如图,连接 ,作 交 于 ,
则 即为所求.
(2) ,
.
而 ,
,
,即 ,
.
答:旗杆 的高为 .
20. 如图所示.
21. (1) 三棱柱
(2) 表面展开图如图所示(答案不唯一).
(3) ,
这个几何体的侧面积为 .
22. (1) 该几何体的主视图和左视图如图所示.
(2)
【解析】给这个几何体喷上颜色(底面不喷色),需要喷色的面有 个,所以喷色的面积为 .
(3)
【解析】在俯视图中标数字“”的正方形的位置上再添加 个小正方体,不会改变主视图和俯视图.
23. (1) 光线及光源所在的位置 如图,
即为 在地面的影子.
(2) 分别延长 , 交于点 ,则 ,,
,
又 ,
,
,
在 中,,
,
乙杆 的高度为 .
24. (1) ,
【解析】球的主视图为圆,长方体的主视图是矩形,圆锥的主视图为等腰三角形,圆柱的主视图为矩形,故填 ,.
(2) 列表如下:
由上表可知,共有 种等可能的结果,其中两次抽出的卡片正面所示立体图形的主视图都是矩形的有 种,分别是 ,,,,所以两次抽出的卡片正面所示立体图形的主视图都是矩形的概率为 ,即 .
(3) 答案不唯一,如选圆柱和圆锥组合,画三视图如下.
