直角三角形[上学期]
图片预览



文档简介
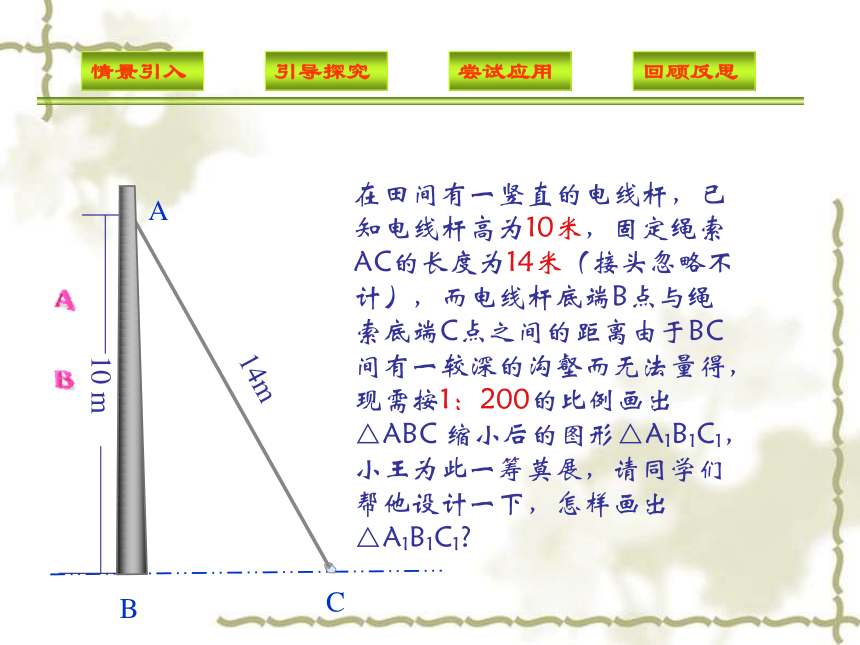
课件17张PPT。ABC10 m14m在田间有一竖直的电线杆,已知电线杆高为10米,固定绳索AC的长度为14米(接头忽略不计),而电线杆底端B点与绳索底端C点之间的距离由于BC间有一较深的沟壑而无法量得,现需按1:200的比例画出△ABC 缩小后的图形△A1B1C1,小王为此一筹莫展,请同学们帮他设计一下,怎样画出△A1B1C1?判定三角形相似有哪些常用方法?相似三角形的预备定理
判定定理一 (两边对应成比例和夹角相等)
判定定理二(两角对应相等)
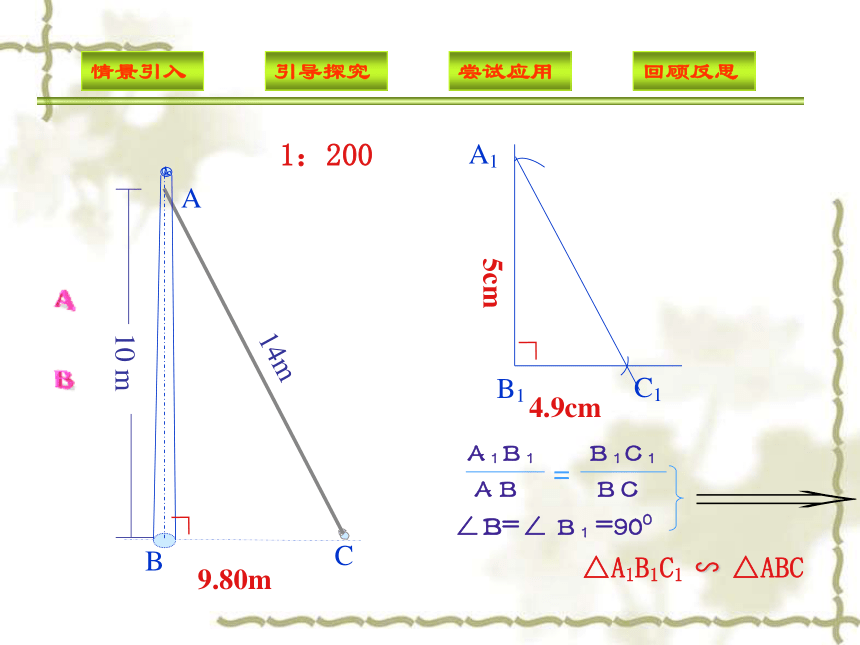
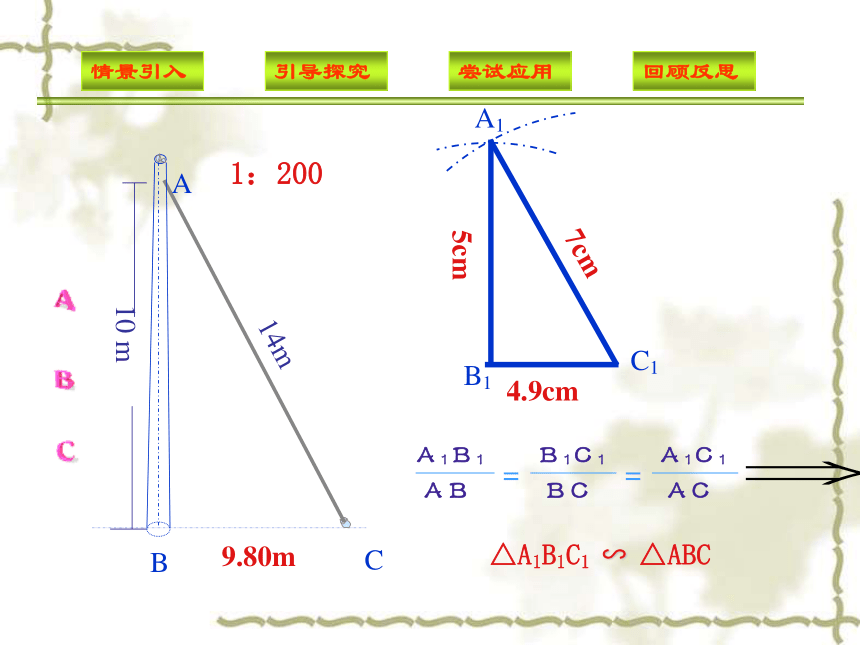
判定定理三 (三边对应成比例)如何运用这些定理解决问题呢? 1:200BC9.80mA10 m14m∟∠B=∠ B 1 =900△A1B1C1 ∽ △ABCC1:200AB10 m14m9.80m△A1B1C1 ∽ △ABCA1ABC10 m14m∟∠B=∠ B 1 =900△A1B1C1 ∽ △ABC1:200
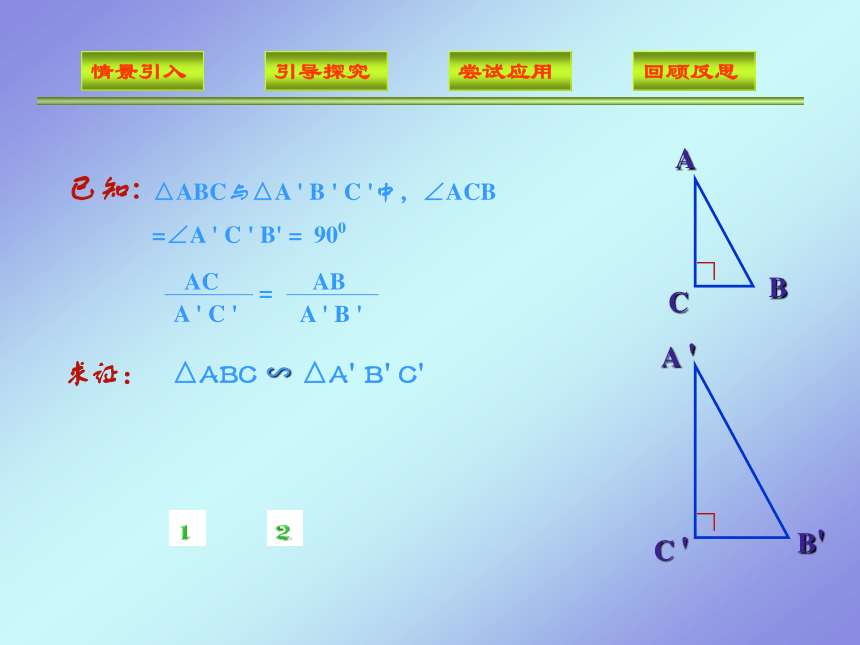
问 题在证明直角三角形全等时有HL,那么斜边和直角边对应成比例的两个直角三角形是否相似△ABC与△A ' B ' C '中,∠ACB
=∠A ' C ' B' = 900已知:AC=K· A'C', AB=K· A'B'BC2=K2( A'B '2- A'C '2)B 'C '2= A ' B'2- A'C '2△ABC ∽ △A' B' C'证明;分别在A' C' ,A' B'上截取A' D =AC,A' E =AB,连结DE。DE∥B' C'?A' DE ∽ ?A' C' B'A' D =ACA' E =AB?A'DE ≌ ?ACB∠A' DE= ∠C' =900△ABC ∽ △A' B' C'∟∟∟得出结论:
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三形相似。简单地说:
斜边和一条直角边对应成比例,两直角三角形相似。依据下列条件判定Rt△ABC和Rt△A′B′C′是否相似
,其中∠C=∠C′=90°。并说明为什么。
(1)∠A=25°,∠B′=65°。
(2)AC=3,BC=4,A′C′=6,则B′C′=8。
(3)AB=10,AC=8,A′B′=15,B′C′=9。 问题一问题二问题三1、定义法和预备定理
2、判定定理一、二、三
3、斜边和一条直角边对 应成比例。
判定直角三角形相似有何方法?问题一问题二问题三问题2:
已知在△ABC中,∠ACB=90o, CD⊥AB
你能找出几对相似三角形?请给予证明。直角三角形被斜边上的高线分成的两个直角三角形和原三角形相似 问题一问题二问题三如图:CE交△ABC的高线AD于点O,交AB于
E,且OC?BD=AB?OD。你能得出哪些结论?等角:……
比例线段:……
相似三角形:……
问题一问题二问题三先独立思考,后分组讨论,最后全班交流,并将所得结论归类总结:1.本节课我们学了哪些内容?
2.你有什么收获与体会?ABD1、必做题:作业本中相应作业。
2、兴趣题:如图,在三角形?ABC 中,∠ACB= 900,在?ABC外有一动点D,D点在运动过程中,始终保持∠ADC = 900,已知AB=10,AC=6,问当AD为多少时, ?ACD与?ABC相似?C106∟∟板书设计
判定定理一 (两边对应成比例和夹角相等)
判定定理二(两角对应相等)
判定定理三 (三边对应成比例)如何运用这些定理解决问题呢? 1:200BC9.80mA10 m14m∟∠B=∠ B 1 =900△A1B1C1 ∽ △ABCC1:200AB10 m14m9.80m△A1B1C1 ∽ △ABCA1ABC10 m14m∟∠B=∠ B 1 =900△A1B1C1 ∽ △ABC1:200
问 题在证明直角三角形全等时有HL,那么斜边和直角边对应成比例的两个直角三角形是否相似△ABC与△A ' B ' C '中,∠ACB
=∠A ' C ' B' = 900已知:AC=K· A'C', AB=K· A'B'BC2=K2( A'B '2- A'C '2)B 'C '2= A ' B'2- A'C '2△ABC ∽ △A' B' C'证明;分别在A' C' ,A' B'上截取A' D =AC,A' E =AB,连结DE。DE∥B' C'?A' DE ∽ ?A' C' B'A' D =ACA' E =AB?A'DE ≌ ?ACB∠A' DE= ∠C' =900△ABC ∽ △A' B' C'∟∟∟得出结论:
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三形相似。简单地说:
斜边和一条直角边对应成比例,两直角三角形相似。依据下列条件判定Rt△ABC和Rt△A′B′C′是否相似
,其中∠C=∠C′=90°。并说明为什么。
(1)∠A=25°,∠B′=65°。
(2)AC=3,BC=4,A′C′=6,则B′C′=8。
(3)AB=10,AC=8,A′B′=15,B′C′=9。 问题一问题二问题三1、定义法和预备定理
2、判定定理一、二、三
3、斜边和一条直角边对 应成比例。
判定直角三角形相似有何方法?问题一问题二问题三问题2:
已知在△ABC中,∠ACB=90o, CD⊥AB
你能找出几对相似三角形?请给予证明。直角三角形被斜边上的高线分成的两个直角三角形和原三角形相似 问题一问题二问题三如图:CE交△ABC的高线AD于点O,交AB于
E,且OC?BD=AB?OD。你能得出哪些结论?等角:……
比例线段:……
相似三角形:……
问题一问题二问题三先独立思考,后分组讨论,最后全班交流,并将所得结论归类总结:1.本节课我们学了哪些内容?
2.你有什么收获与体会?ABD1、必做题:作业本中相应作业。
2、兴趣题:如图,在三角形?ABC 中,∠ACB= 900,在?ABC外有一动点D,D点在运动过程中,始终保持∠ADC = 900,已知AB=10,AC=6,问当AD为多少时, ?ACD与?ABC相似?C106∟∟板书设计
