解直角三角形的应用2.[下学期]
图片预览

文档简介
课件17张PPT。第十九章
解直角三角形的
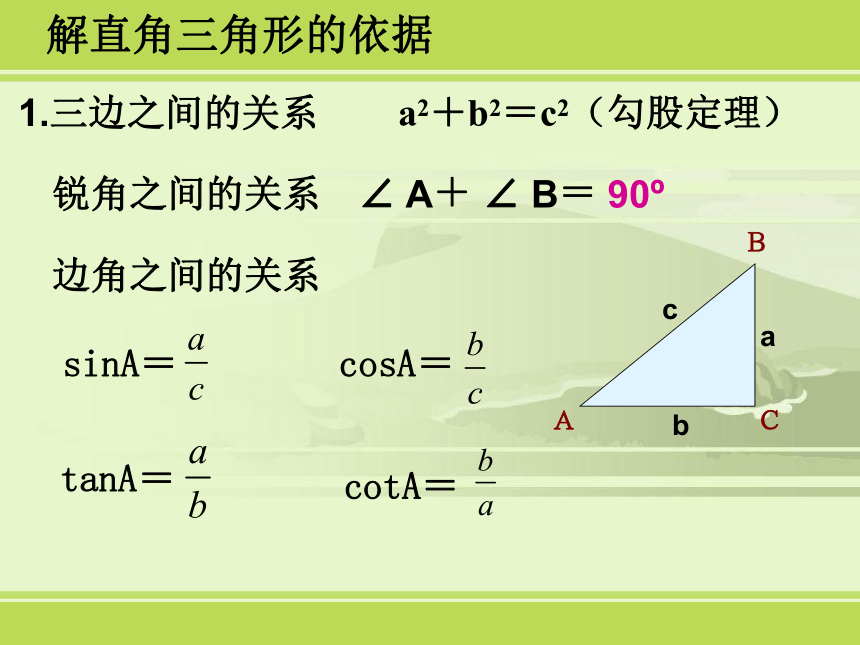
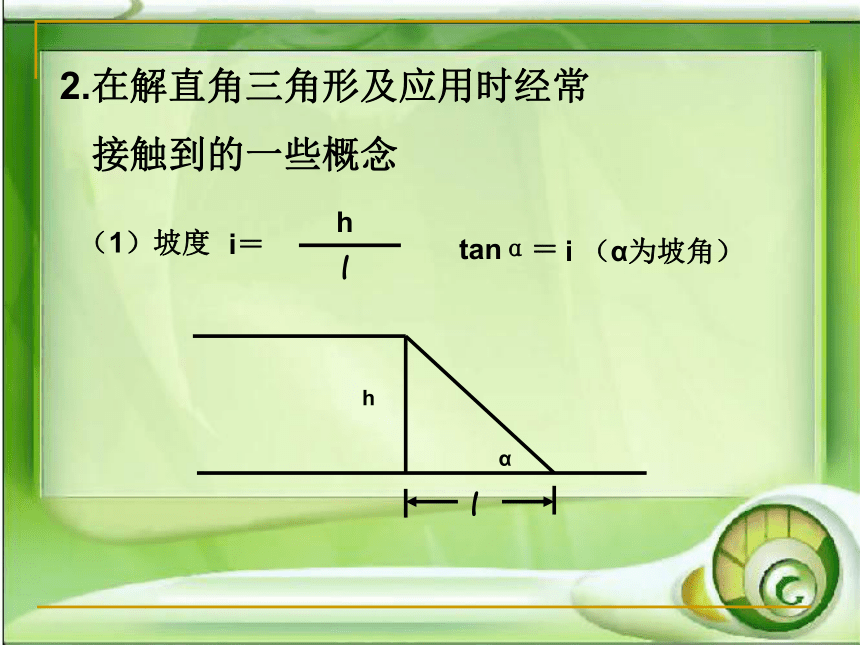
应用1.三边之间的关系a2+b2=c2(勾股定理)锐角之间的关系∠ A+ ∠ B= 90o边角之间的关系tanA=sinA=cotA=解直角三角形的依据cosA=2.在解直角三角形及应用时经常
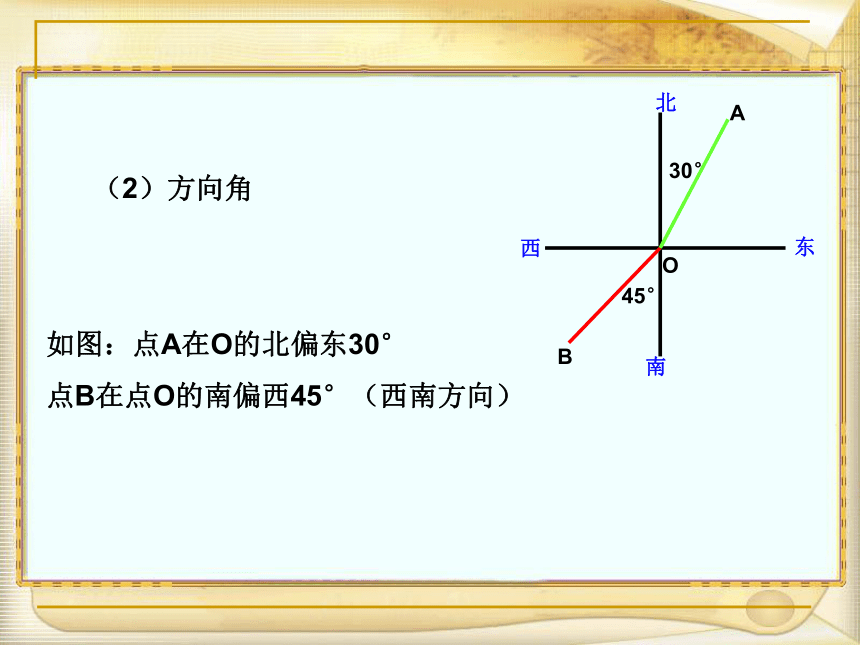
接触到的一些概念(2)方向角如图:点A在O的北偏东30°
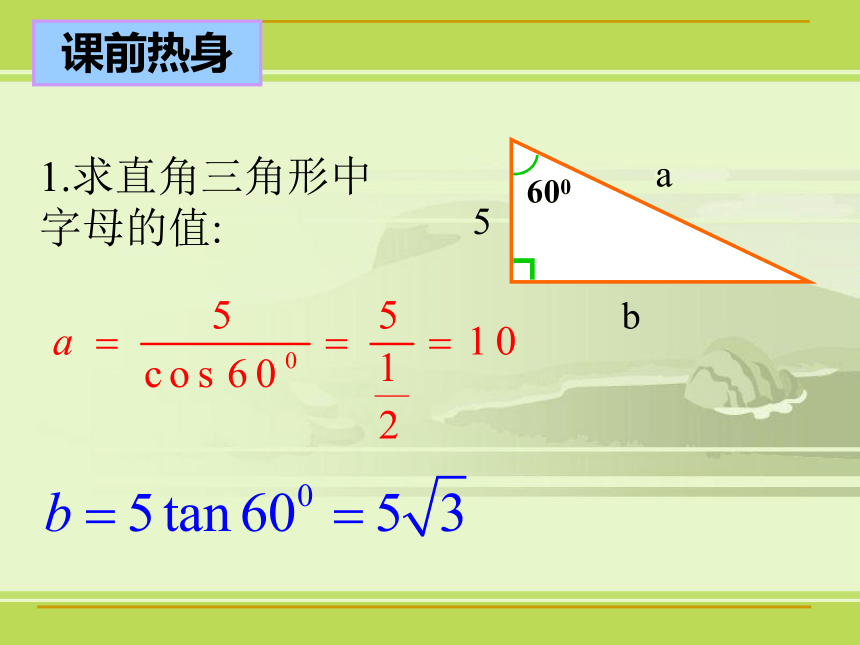
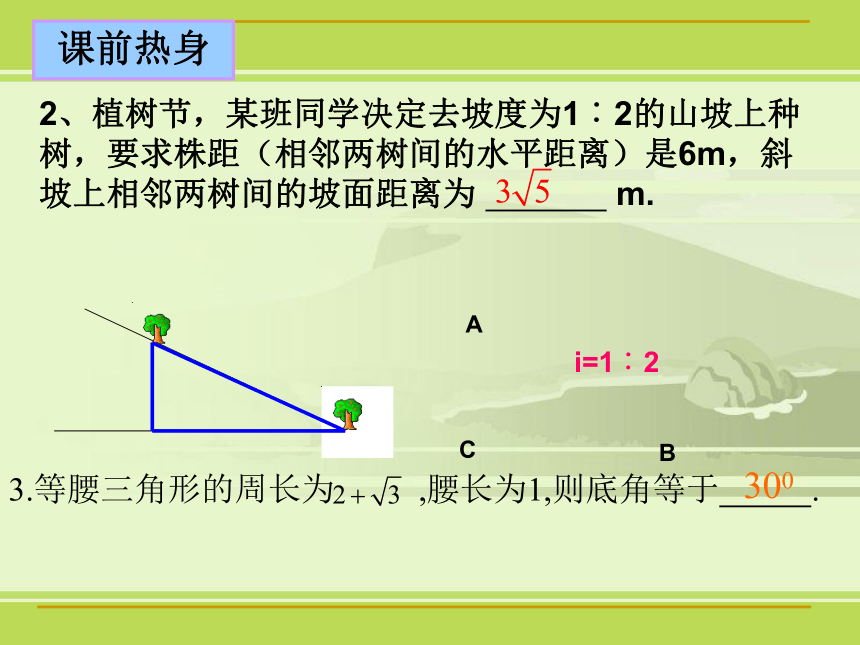
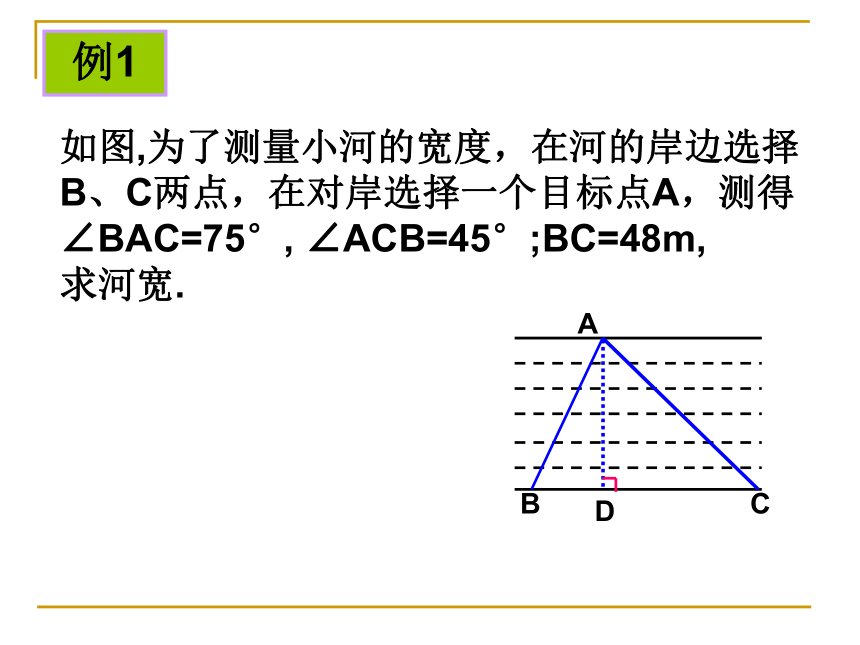
点B在点O的南偏西45°(西南方向)课前热身1.求直角三角形中字母的值:课前热身2、植树节,某班同学决定去坡度为1︰2的山坡上种树,要求株距(相邻两树间的水平距离)是6m,斜坡上相邻两树间的坡面距离为 m.ACBi=1︰23.等腰三角形的周长为 ,腰长为1,则底角等于 .300如图,为了测量小河的宽度,在河的岸边选择B、C两点,在对岸选择一个目标点A,测得∠BAC=75°, ∠ACB=45°;BC=48m,
求河宽.D例1海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60?,航行24海里到C,见岛A在北偏西30?,货轮继续向西航行,有无触礁的危险?请说明理由.例2你会画出图形吗?请试一试.解题的基本步骤:(1)理解题意,画出草图
(2)转化问题,把实际问题
转化为数学问题
(3)选择关系(式),选择
适当的边角关系
(4)准确解答,按要求精确计算如图学校里有一块三角形形状的花圃ABC,现测得∠A=30°, AC=40m,BC=25m,请你帮助计算一下这块花圃的面积?D解:过点C作CD⊥AB于D在Rt△ADC中, ∠A=30°, AC=40,在Rt△CDB中,CD=20, CB=25,随堂练习300山顶上有一旗杆,在地面上一点A处测得杆顶B的仰角为 600,杆底C的仰角为450,已知旗杆高BC=20米,求山高CD。随堂练习1.本节例题学习以后,我们可以得到解
直角三角形的两种基本图形:小结:2.学会把实际问题转化成数学问题;会用
方程思想解决问题.作业课本:P121 14、15、16 由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。思考(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响 的时间有多长?解(2):设点E、F是以A为圆心,150km为半径的圆与BM的交点,由题意得:∴EF = 2CE = 2 x 90 = 180∴A城受到沙尘暴影响的时间为180÷12 = 15小时答:A城将受到这次沙尘暴影响,影响的时间为15小时。随堂练习某市计划将地处A、B两地的两所大学合并成一所综合大学,为了方便A、B两地师生的交往,学校准备在相距2千米的A、B两地之间修筑一条笔直公路(即图中的线段AB)经测量,在A地的北偏东60o方向,B地的西偏北45o方向的C处有一个半径为0.7千米的公园,问计划修筑的这条公路会不会穿过公园?为什么?D随堂练习如图,一人在河对岸C处测得电视塔尖A的仰角为45o,后退100米到达D处,测得塔尖A的仰角为30o,设塔底B与C、D在同一直线上, 求电视塔的高度AB。思想方法小结:转化思想贯穿全章。把实际问题转化为数学问题。
数形结合思想。画出图形,使已知元素和未知元素更直观。
函数思想。锐角的四个三角函数,角度与函数值一一对应。
方程思想。若某个元素无法直接求解,往往设未知数,根据三角形的边角关系列出方程。
接触到的一些概念(2)方向角如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)课前热身1.求直角三角形中字母的值:课前热身2、植树节,某班同学决定去坡度为1︰2的山坡上种树,要求株距(相邻两树间的水平距离)是6m,斜坡上相邻两树间的坡面距离为 m.ACBi=1︰23.等腰三角形的周长为 ,腰长为1,则底角等于 .300如图,为了测量小河的宽度,在河的岸边选择B、C两点,在对岸选择一个目标点A,测得∠BAC=75°, ∠ACB=45°;BC=48m,
求河宽.D例1海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60?,航行24海里到C,见岛A在北偏西30?,货轮继续向西航行,有无触礁的危险?请说明理由.例2你会画出图形吗?请试一试.解题的基本步骤:(1)理解题意,画出草图
(2)转化问题,把实际问题
转化为数学问题
(3)选择关系(式),选择
适当的边角关系
(4)准确解答,按要求精确计算如图学校里有一块三角形形状的花圃ABC,现测得∠A=30°, AC=40m,BC=25m,请你帮助计算一下这块花圃的面积?D解:过点C作CD⊥AB于D在Rt△ADC中, ∠A=30°, AC=40,在Rt△CDB中,CD=20, CB=25,随堂练习300山顶上有一旗杆,在地面上一点A处测得杆顶B的仰角为 600,杆底C的仰角为450,已知旗杆高BC=20米,求山高CD。随堂练习1.本节例题学习以后,我们可以得到解
直角三角形的两种基本图形:小结:2.学会把实际问题转化成数学问题;会用
方程思想解决问题.作业课本:P121 14、15、16 由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。思考(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响 的时间有多长?解(2):设点E、F是以A为圆心,150km为半径的圆与BM的交点,由题意得:∴EF = 2CE = 2 x 90 = 180∴A城受到沙尘暴影响的时间为180÷12 = 15小时答:A城将受到这次沙尘暴影响,影响的时间为15小时。随堂练习某市计划将地处A、B两地的两所大学合并成一所综合大学,为了方便A、B两地师生的交往,学校准备在相距2千米的A、B两地之间修筑一条笔直公路(即图中的线段AB)经测量,在A地的北偏东60o方向,B地的西偏北45o方向的C处有一个半径为0.7千米的公园,问计划修筑的这条公路会不会穿过公园?为什么?D随堂练习如图,一人在河对岸C处测得电视塔尖A的仰角为45o,后退100米到达D处,测得塔尖A的仰角为30o,设塔底B与C、D在同一直线上, 求电视塔的高度AB。思想方法小结:转化思想贯穿全章。把实际问题转化为数学问题。
数形结合思想。画出图形,使已知元素和未知元素更直观。
函数思想。锐角的四个三角函数,角度与函数值一一对应。
方程思想。若某个元素无法直接求解,往往设未知数,根据三角形的边角关系列出方程。
