25.3解直角三角形[上学期]
图片预览




文档简介
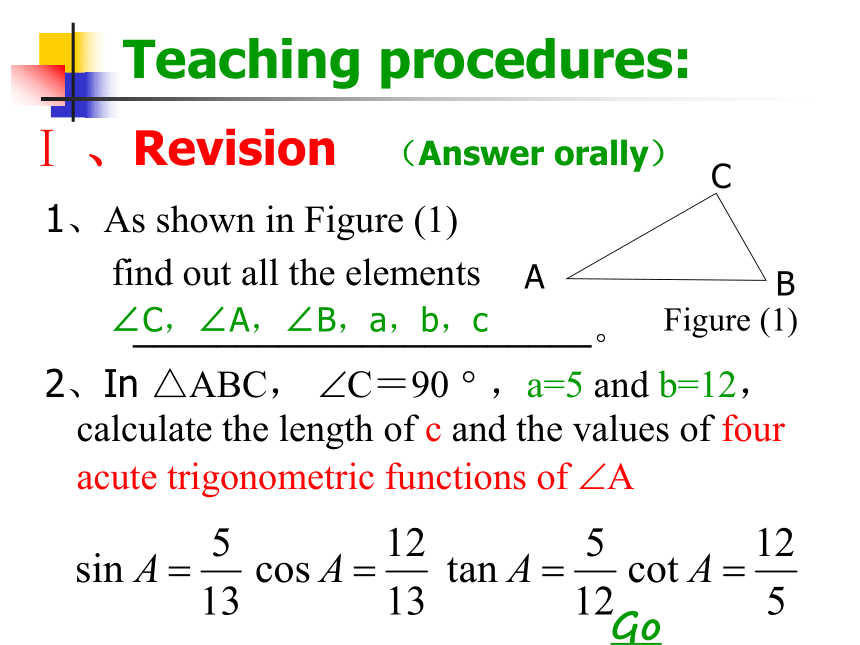
课件19张PPT。Class begins6.4 Solving Right TrianglesⅠ Teaching Aims Ⅱ Teaching Key pointsⅢ Teaching difficulties Ⅳ Teaching proceduresTeaching aims of the lessonⅠ 、To know the definition of solving right triangleⅡ 、To understand the relationships among other five elements.Ⅲ 、To master how to solve right triangleGo backTeaching expressions:Ⅱ 、To solve right triangles according to given conditions.Ⅰ 、To know how to solve right triangle.Teaching difficult pointsGo backⅠ 、Revision (Answer orally)1、As shown in Figure (1)
find out all the elements
______________________。
2、In △ABC, ?C=90 ? ,a=5 and b=12,calculate the length of c and the values of four acute trigonometric functions of ?A∠C,∠A,∠B,a,b,cTeaching procedures:Figure (1)Go back1.The ways of solving maths problem 从上面的三个式子中,你可以总结出什么规律?(1).Given:a=b+c,if a=5,b=7,c=____. 在计算过程中,要充分利用只含一个未知数的计算式Ⅱ 、presentation-230°(2).Given: ,if a=2,b=2 , ?A =____.(3).Given: ,ifa= ,?A=60 ?,c=____.
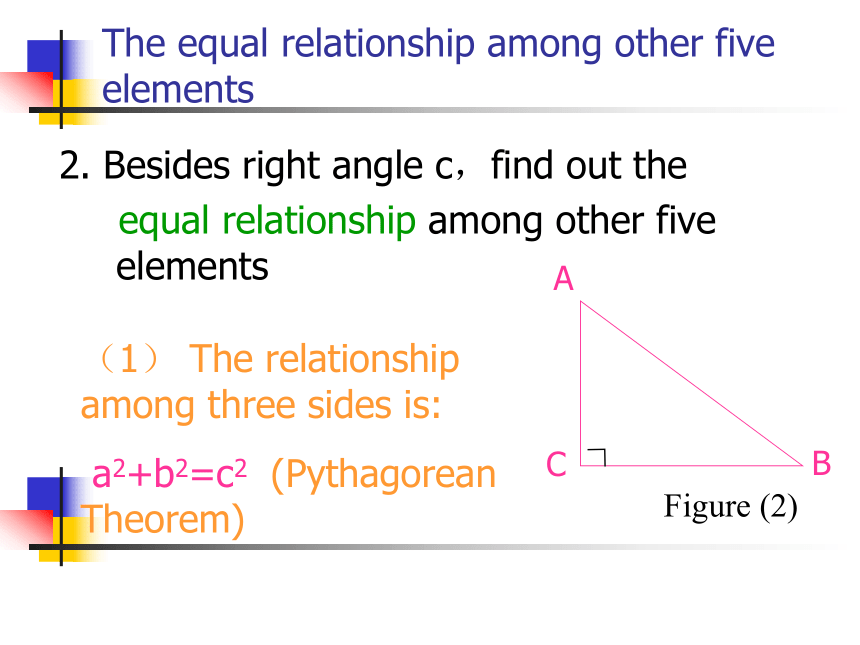
42. Besides right angle c,find out the
equal relationship among other five elements(1) The relationship among three sides is:
a2+b2=c2 (Pythagorean Theorem)Figure (2)The equal relationship among other five elementsThe equal relationship among other five elements(2)The relationship between two acute
angles is:
?A+ ? B= 90 ?(3)The relationship among sides and
angles are:
3.Think it over:Applying these relationships, if we know the other two elements , Can we find out three unknown elements?Example: if ?A and c are given ,
?B=_________, a=_______,
b=________,________,__________c sin A90 ?- ?Ab = a cot Ab =4.Training Exercises (P211)Answers:(4) ?A = 90 ? - ?B
b = a tan B c = b sin B(3) ?B = 90 ? - ?A
a = b tan A c = b cos A(2)
(use calculators ?A)
?B = 90 ? - ?A
书山有路勤为径,学海无涯苦作舟,5.Example 1: In △ABC,?C is a right angle,the opposite sides of ?A, ?B and ?C are a,b and c, c=287.4,and ?B= 42 ?6′.Solve this triangle. Solution:① ?A= 90 ? - 42 ?6′= 47 ?54′ ∴ a =ccos B =287.4 × 0.7420
≈213.3 ∴ b=csin B =287.4 × 0.6704
≈192.7② ∵ cos B = ③ ∵ sin B = 计算的最后结果,角度通常精确到分,边长保留四个有效数字。 6.Training Exercises (P212(1))辛勤的汗水造就天才!7.Example 2: IN Rt△ABC ,a=104.0,and b=20.49. Solve this triangle.Solution:①
∴② ?B= 90 ? - 78 ?51′= 11 ?9′③ ∵ sin A = ?A= 78 ?51′ (Using calculator)8.Training Exercises P21 2(2)Solution:(1) (2) ?A=90 ? - 20 ?47′ =69?13′(3) a = 0.7786?B=20?47′turn to page 19.Return to the question raised in the introduction part of this chapter.ACB105.2m?A=30?60′?Ⅲ.summary:归纳得出:本节课我们主要学习了怎样解直角三角形,关键要抓住五个元素之间的等量关系,进行变形处理。解题过程中要尽量采用原始数据,计算结果按题目要求进行精确。(通常角度精确到分,边长取四位有效数字)。
Ⅳ.Homework: P32(3)7.DiscussionsExample: Given a,b,solving right
triangle ?B=_______, ?A=_______,
c=_______,Example: Given a=2,b=4,
tanA=_______, ?A=_______,
find out all the elements
______________________。
2、In △ABC, ?C=90 ? ,a=5 and b=12,calculate the length of c and the values of four acute trigonometric functions of ?A∠C,∠A,∠B,a,b,cTeaching procedures:Figure (1)Go back1.The ways of solving maths problem 从上面的三个式子中,你可以总结出什么规律?(1).Given:a=b+c,if a=5,b=7,c=____. 在计算过程中,要充分利用只含一个未知数的计算式Ⅱ 、presentation-230°(2).Given: ,if a=2,b=2 , ?A =____.(3).Given: ,ifa= ,?A=60 ?,c=____.
42. Besides right angle c,find out the
equal relationship among other five elements(1) The relationship among three sides is:
a2+b2=c2 (Pythagorean Theorem)Figure (2)The equal relationship among other five elementsThe equal relationship among other five elements(2)The relationship between two acute
angles is:
?A+ ? B= 90 ?(3)The relationship among sides and
angles are:
3.Think it over:Applying these relationships, if we know the other two elements , Can we find out three unknown elements?Example: if ?A and c are given ,
?B=_________, a=_______,
b=________,________,__________c sin A90 ?- ?Ab = a cot Ab =4.Training Exercises (P211)Answers:(4) ?A = 90 ? - ?B
b = a tan B c = b sin B(3) ?B = 90 ? - ?A
a = b tan A c = b cos A(2)
(use calculators ?A)
?B = 90 ? - ?A
书山有路勤为径,学海无涯苦作舟,5.Example 1: In △ABC,?C is a right angle,the opposite sides of ?A, ?B and ?C are a,b and c, c=287.4,and ?B= 42 ?6′.Solve this triangle. Solution:① ?A= 90 ? - 42 ?6′= 47 ?54′ ∴ a =ccos B =287.4 × 0.7420
≈213.3 ∴ b=csin B =287.4 × 0.6704
≈192.7② ∵ cos B = ③ ∵ sin B = 计算的最后结果,角度通常精确到分,边长保留四个有效数字。 6.Training Exercises (P212(1))辛勤的汗水造就天才!7.Example 2: IN Rt△ABC ,a=104.0,and b=20.49. Solve this triangle.Solution:①
∴② ?B= 90 ? - 78 ?51′= 11 ?9′③ ∵ sin A = ?A= 78 ?51′ (Using calculator)8.Training Exercises P21 2(2)Solution:(1) (2) ?A=90 ? - 20 ?47′ =69?13′(3) a = 0.7786?B=20?47′turn to page 19.Return to the question raised in the introduction part of this chapter.ACB105.2m?A=30?60′?Ⅲ.summary:归纳得出:本节课我们主要学习了怎样解直角三角形,关键要抓住五个元素之间的等量关系,进行变形处理。解题过程中要尽量采用原始数据,计算结果按题目要求进行精确。(通常角度精确到分,边长取四位有效数字)。
Ⅳ.Homework: P32(3)7.DiscussionsExample: Given a,b,solving right
triangle ?B=_______, ?A=_______,
c=_______,Example: Given a=2,b=4,
tanA=_______, ?A=_______,
