解直角三角形[下学期]
图片预览




文档简介
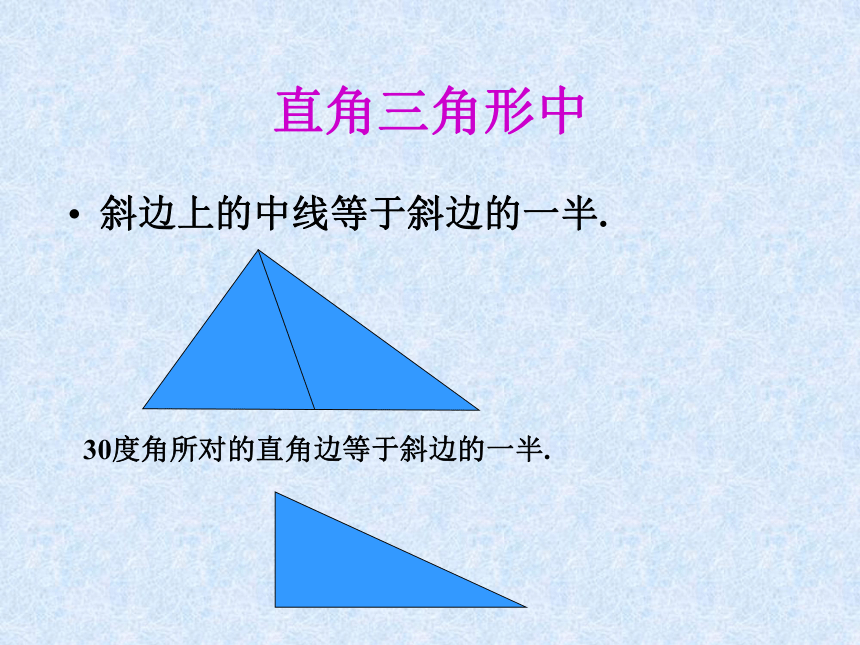
课件15张PPT。直角三角形直角三角形中斜边上的中线等于斜边的一半.
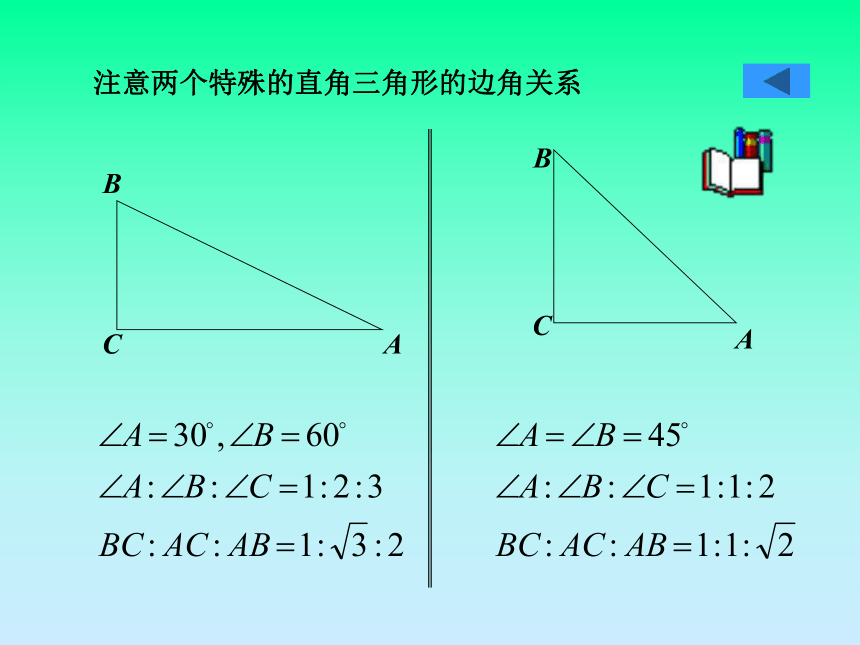
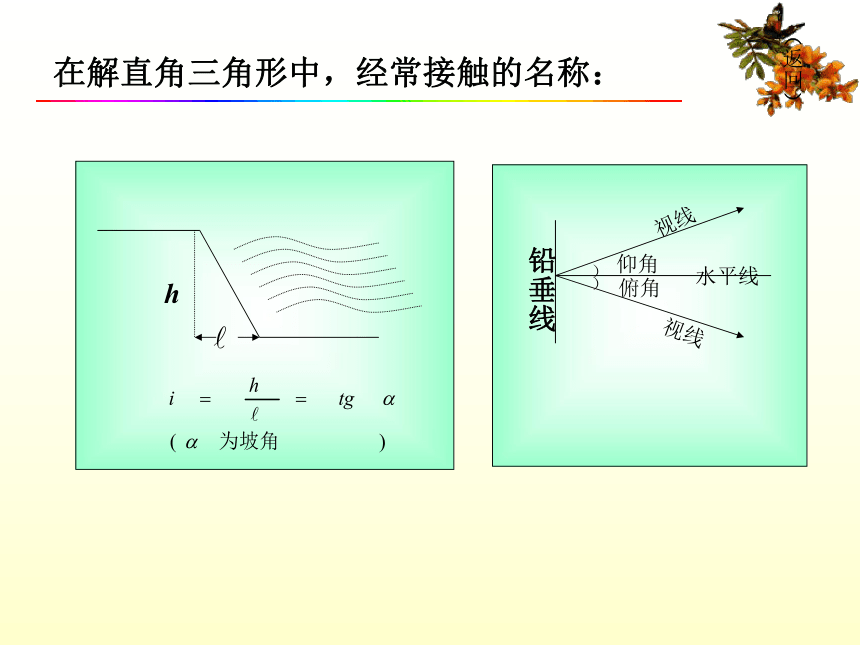
30度角所对的直角边等于斜边的一半.返回特殊角的三角函数值 注意两个特殊的直角三角形的边角关系在一个直角三角形中,已知一条边和一个锐角或者已知两条边,可以求出其他的边和角,这就是解直角三角形.在解直角三角形中,经常接触的名称:(返回)在解直角三角形中,经常接触的名称:(返回)ABC点C在点A的南偏东50°
点B在点A的北偏东55°
点A在点B的
点A在点C的 南偏西55°北偏西50°方向角例 1 在直角三角形ABC中,∠C=90度,BC=35,AB=45,解直角三角形.(角度精确到1度,边长保留两个有效数字.)解:∵AC2=AB2-BC2=452-352=800 ∴AC≈28
∵tanA= ∴∠ A=51°
∴∠B=90°-∠A=39°例2.已知: △ABC中,∠A=105°,∠C=45°,BC=8,
求 AC和AB的长.D[评析]在解斜三角形、等腰三角形、梯形等一些图形的问题时,可以适当地添加辅助线构造直角三角形,然后利用解直角三角形,使问题得以解决.设未知数得到相关的方程,是解本题的一个关键步骤,应用了方程的思想,将几何图形的计算转化为解代数方程.解:过A作AD⊥BC,垂足为D,
则∠DAC=∠C=45°,AD=DC
∠BAD=105°-45°==60°
设DC=X=AD,BD=8-X,得 tan60 =
解得 X=4(√3-1) AB=2X
AC=√2X 例3:在山脚C处测得山顶A的仰角为45°.问题如下:
1.沿着水平地面向前300m到达D点,在D点测得山顶A的仰角为60 °,求山高AB.
2.沿着坡角为30 °的斜坡前进300m到达D点,在D点测得山顶A的仰角为60 ° ,求山高AB.Dx 例3:在山脚C处测得山顶A的仰角为45°.问题如下:
1.沿着水平地面向前300m到达D点,在D点测得山顶A的仰角为60 °,求山高AB.
2.沿着坡角为30 °的斜坡前进300m到达D点,在D点测得山顶A的仰角为60 ° ,求山高AB.DEFxx 1、在Rt △ABC中, ∠ C=90°,∠A的正切等于2,BC=6,则这个三角形的面积等于____________,斜边AB=_______________ .基础训练 2、某人沿着坡角为45 °的斜坡走了310 m,则此人的垂直高度增加了____________m . 3、已知堤坝的横断面是等腰梯形ABCD,上底CD的宽为a,下底AB的宽为b,坝高为h,则堤坝的坡度i=_______________(用a,b,h表示). 4、已知:等腰△ABC的底边长为4,底角正弦为 ,求它的腰长. 5、已知: △ABC中,AB=AC,BD为△ABC的一条高线,D为垂足,且BD= AB=1,求tgC的值. 6、已知: △ABC中,D为AB的中点,∠ACB=135°,AC⊥CD,求sinA的值.E三、小结 解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系.
30度角所对的直角边等于斜边的一半.返回特殊角的三角函数值 注意两个特殊的直角三角形的边角关系在一个直角三角形中,已知一条边和一个锐角或者已知两条边,可以求出其他的边和角,这就是解直角三角形.在解直角三角形中,经常接触的名称:(返回)在解直角三角形中,经常接触的名称:(返回)ABC点C在点A的南偏东50°
点B在点A的北偏东55°
点A在点B的
点A在点C的 南偏西55°北偏西50°方向角例 1 在直角三角形ABC中,∠C=90度,BC=35,AB=45,解直角三角形.(角度精确到1度,边长保留两个有效数字.)解:∵AC2=AB2-BC2=452-352=800 ∴AC≈28
∵tanA= ∴∠ A=51°
∴∠B=90°-∠A=39°例2.已知: △ABC中,∠A=105°,∠C=45°,BC=8,
求 AC和AB的长.D[评析]在解斜三角形、等腰三角形、梯形等一些图形的问题时,可以适当地添加辅助线构造直角三角形,然后利用解直角三角形,使问题得以解决.设未知数得到相关的方程,是解本题的一个关键步骤,应用了方程的思想,将几何图形的计算转化为解代数方程.解:过A作AD⊥BC,垂足为D,
则∠DAC=∠C=45°,AD=DC
∠BAD=105°-45°==60°
设DC=X=AD,BD=8-X,得 tan60 =
解得 X=4(√3-1) AB=2X
AC=√2X 例3:在山脚C处测得山顶A的仰角为45°.问题如下:
1.沿着水平地面向前300m到达D点,在D点测得山顶A的仰角为60 °,求山高AB.
2.沿着坡角为30 °的斜坡前进300m到达D点,在D点测得山顶A的仰角为60 ° ,求山高AB.Dx 例3:在山脚C处测得山顶A的仰角为45°.问题如下:
1.沿着水平地面向前300m到达D点,在D点测得山顶A的仰角为60 °,求山高AB.
2.沿着坡角为30 °的斜坡前进300m到达D点,在D点测得山顶A的仰角为60 ° ,求山高AB.DEFxx 1、在Rt △ABC中, ∠ C=90°,∠A的正切等于2,BC=6,则这个三角形的面积等于____________,斜边AB=_______________ .基础训练 2、某人沿着坡角为45 °的斜坡走了310 m,则此人的垂直高度增加了____________m . 3、已知堤坝的横断面是等腰梯形ABCD,上底CD的宽为a,下底AB的宽为b,坝高为h,则堤坝的坡度i=_______________(用a,b,h表示). 4、已知:等腰△ABC的底边长为4,底角正弦为 ,求它的腰长. 5、已知: △ABC中,AB=AC,BD为△ABC的一条高线,D为垂足,且BD= AB=1,求tgC的值. 6、已知: △ABC中,D为AB的中点,∠ACB=135°,AC⊥CD,求sinA的值.E三、小结 解直角三角形的关键是找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作辅助线构筑直角三角形(作某边上的高是常用的辅助线);当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题化归为直角三角形中的边角关系.
