2021-2022学年天津市七年级下学期人教版数学期末试题选编第七章平面直角坐标系练习题(含解析)
文档属性
| 名称 | 2021-2022学年天津市七年级下学期人教版数学期末试题选编第七章平面直角坐标系练习题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 799.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-29 23:37:05 | ||
图片预览



文档简介
第七章:平面直角坐标系
一、单选题
1.(2022春·天津河西·七年级统考期末)在平面直角坐标系中,点,,,若轴,则线段BC的最小值及此时点C的坐标分别为( )
A.3, B.10, C.1, D.6,
2.(2022春·天津南开·七年级统考期末)若点M在第四象限,且M到x轴的距离为1,到y轴的距离为2,则点M的坐标为( )
A.(1,-2) B.(2,1) C.(-2,1) D.(2,-1)
3.(2022春·天津西青·七年级统考期末)已知点是平面直角坐标系中轴上一点,且在轴的左侧,若点到轴的距离为3,则点的坐标为( )
A. B. C. D.
4.(2022春·天津河西·七年级统考期末)在平面直角坐标系中,点A(2,-3)所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.(2022春·天津南开·七年级统考期末)若M()满足,点M所在的象限是( )
A.第一、二象限 B.第一、三象限 C.第二、四象限 D.不能确定
6.(2022春·天津东丽·七年级统考期末)在平面直角坐标系中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”例如:三点坐标分别为,,,则“水平底”,“铅垂高”,“矩面积”若、,三点的“矩面积”为15,则t的值为( )
A.或7 B.或6 C.或7 D.或6
7.(2022春·天津津南·七年级统考期末)如图,在四边形ABCD中,ADBC轴,下列说法中正确的是( ).
A.点A与点D的纵坐标相同
B.点A与点B的横坐标相同
C.点A与点C的纵坐标相同
D.点B与点D的横坐标相同
8.(2022春·天津滨海新·七年级统考期末)若点在y轴上,则点P的坐标是( )
A. B. C. D.
9.(2022春·天津宝坻·七年级统考期末)已知线段CD是由线段AB平移得到的,点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为( )
A.(1,2) B.(2,9) C.(5,3) D.(–9,–4)
10.(2022春·天津东丽·七年级统考期末)点 A 的位置如图所示,则关于点 A 的位置下列说法中正确的是( )
A.距点处
B.北偏东 方向上处
C.在点北偏东 方向上处
D.在点北偏东 方向上距点处
二、填空题
11.(2022春·天津滨海新·七年级统考期末)已知点M坐标为且M点到两坐标轴的距离相等,则点的M坐标是________.
12.(2022春·天津南开·七年级统考期末)如果点在轴上,则________;
13.(2022春·天津宝坻·七年级统考期末)在平面直角坐标系中,点的坐标为.若线段轴,且的长为5,则点的坐标为_________.
14.(2022春·天津南开·七年级统考期末)如图,在平面直角坐标系中,,,,……根据这个规律,探究可得点的坐标是_____.
15.(2022春·天津红桥·七年级统考期末)在平面直角坐标系中,如果点在第四象限,则m的取值范围是______.
16.(2022春·天津西青·七年级统考期末)如图是某学校的部分平面示意图,在同一平面直角坐标系中,若体育馆的坐标为,科技馆的坐标为,则教学楼的坐标为______.
三、解答题
17.(2022春·天津宝坻·七年级统考期末)已知点,,.
(1)在平面直角坐标系中描出,,三点;
(2)求的面积;
(3)若点在轴上,当的面积为6时,请直接写出点的坐标.
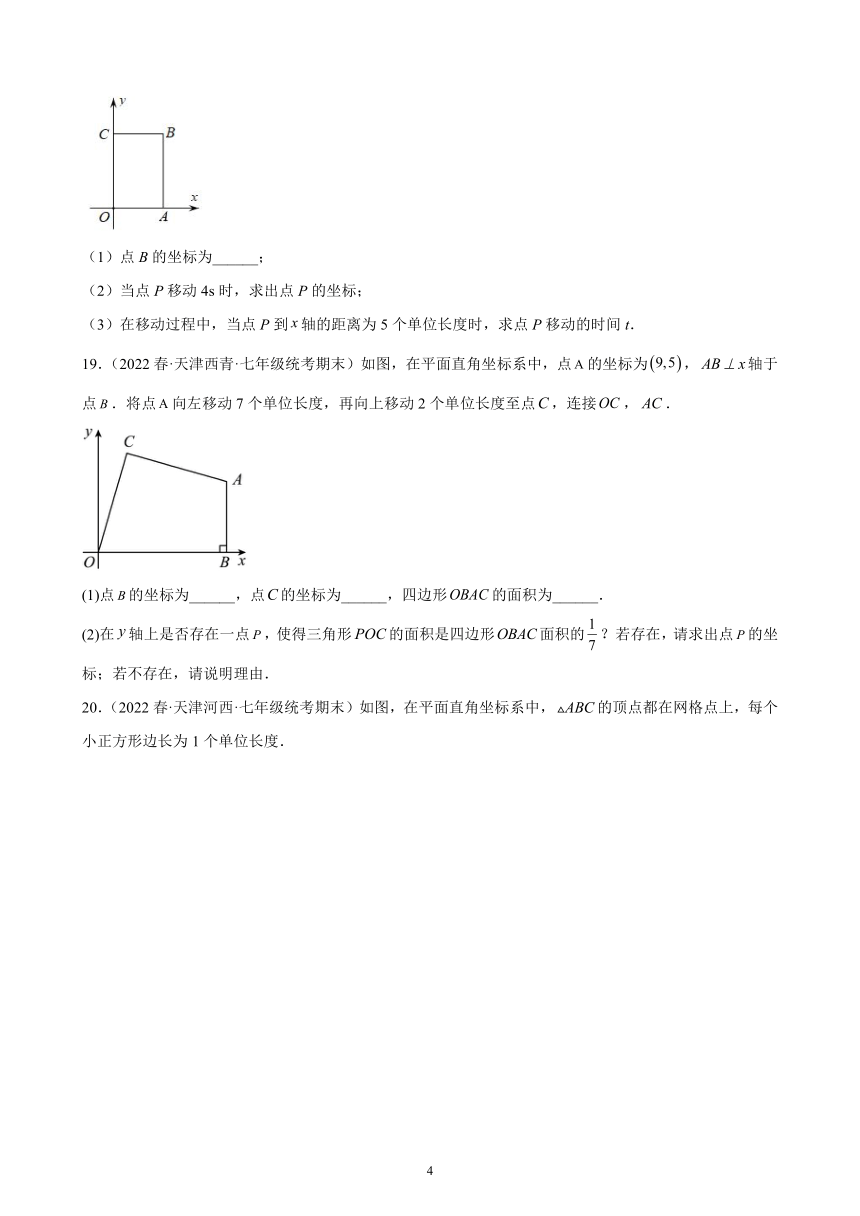
18.(2022春·天津河西·七年级统考期末)如图,在平面直角坐标系中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形的边逆时针移动一周(即:沿着O→A→B→C→O的路线移动).
(1)点B的坐标为______;
(2)当点P移动4s时,求出点P的坐标;
(3)在移动过程中,当点P到轴的距离为5个单位长度时,求点P移动的时间t.
19.(2022春·天津西青·七年级统考期末)如图,在平面直角坐标系中,点的坐标为,轴于点.将点向左移动7个单位长度,再向上移动2个单位长度至点,连接,.
(1)点的坐标为______,点的坐标为______,四边形的面积为______.
(2)在轴上是否存在一点,使得三角形的面积是四边形面积的?若存在,请求出点的坐标;若不存在,请说明理由.
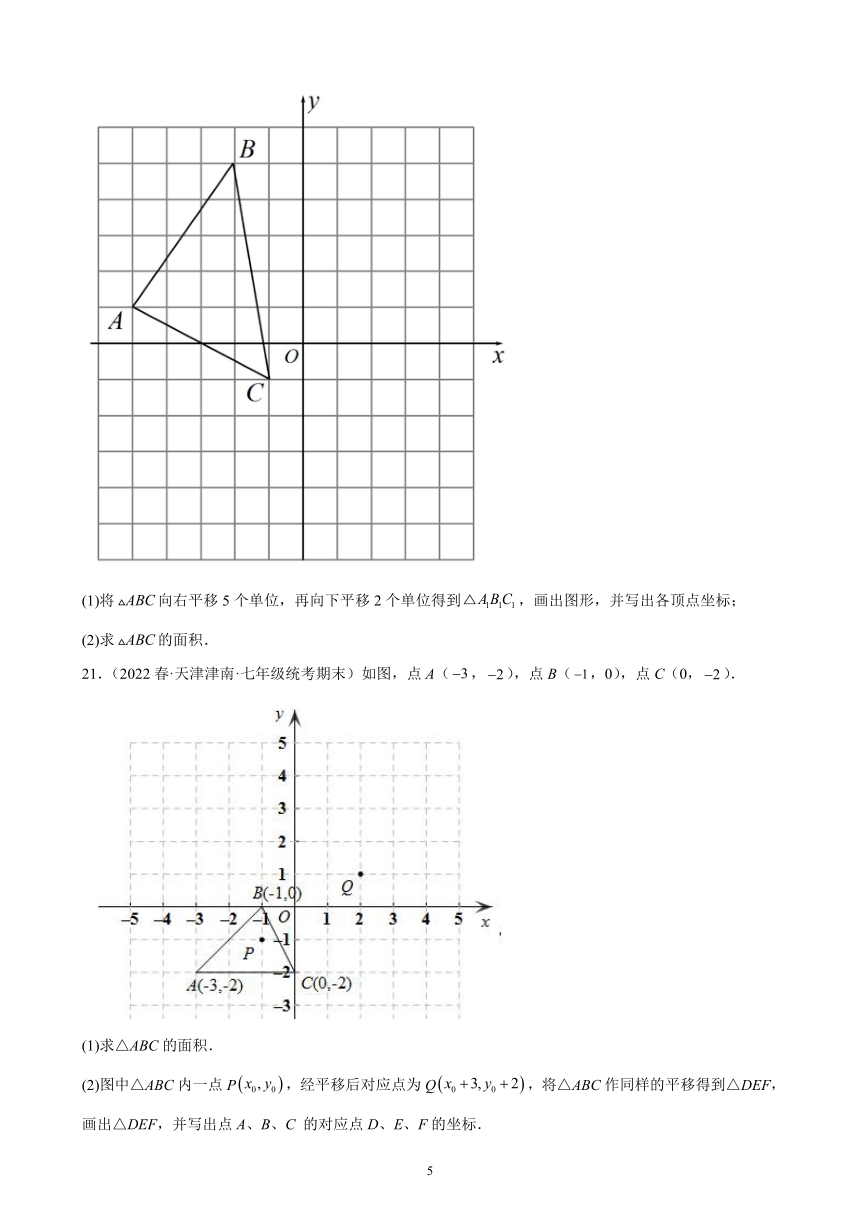
20.(2022春·天津河西·七年级统考期末)如图,在平面直角坐标系中,的顶点都在网格点上,每个小正方形边长为1个单位长度.
(1)将向右平移5个单位,再向下平移2个单位得到,画出图形,并写出各顶点坐标;
(2)求的面积.
21.(2022春·天津津南·七年级统考期末)如图,点A(,),点B(,0),点C(0,).
(1)求△ABC的面积.
(2)图中△ABC内一点P,经平移后对应点为Q,将△ABC作同样的平移得到△DEF,画出△DEF,并写出点A、B、C 的对应点D、E、F的坐标.
参考答案:
1.A
【分析】根据坐标的定义可求得y值,根据线段BC最小,确定BC⊥AC,垂足为点C,进一步求得BC的最小值和点C的坐标.
【详解】解:依题意可得:
∵AC∥x轴,A(-3,2)
∴y=2,
根据垂线段最短,当BC⊥AC于点C时,
点B到AC的距离最短,即BC的最小值=5-2=3,
此时点C的坐标为(3,2),
故选:A.
【点睛】本题考查已知点求坐标及如何根据坐标描点,正确画图即可求解.
2.D
【分析】先判断出点的横、纵坐标的符号,再根据点到轴、轴的距离即可得.
【详解】解:点在第四象限,
点的横坐标为正数,纵坐标为负数,
点到轴的距离为1,到轴的距离为2,
点的纵坐标为,横坐标为2,
即,
故选:D.
【点睛】本题考查了点坐标,熟练掌握各象限内的点坐标的符号规律是解题关键.
3.B
【分析】根据x轴上点的纵坐标为0,到y轴的距离等于横坐标的绝对值解答.
【详解】解:∵点P在x轴上,且在轴的左侧,到y轴的距离为3,
∴点P的坐标为(-3,0).
故选:B.
【点睛】本题考查了点的坐标,熟记x轴上点的纵坐标为0,到y轴的距离等于横坐标的绝对值是解题的关键.
4.D
【分析】根据平面直角坐标系中,各象限内的点坐标的符号规律即可得.
【详解】解:点的横坐标为,纵坐标为,
点所在的象限为第四象限,
故选:D.
【点睛】本题考查了点所在的象限,熟练掌握平面直角坐标系中,各象限内的点坐标的符号规律是解题关键.
5.B
【分析】由条件可得则同号,从而可得答案.
【详解】解:∵,
∴同号,
∴M()在第一或第三象限,
故选B
【点睛】本题考查了平面直角坐标系内点的坐标问题,求出x、y同号是解题的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
6.D
【分析】根据题意可以求得a的值,然后再对t进行讨论,即可求得t的值.
【详解】解:由题意得:
“水平底”为:,
当时,,
则,
解得:;
当时,,
故此种情况不符合题意;
当时,,
则,
解得:.
故选:D.
【点睛】本题考查坐标与图形的性质,解答本题的关键是明确题目中的新定义,利用新定义解答问题.
7.A
【分析】根据平行四边形的性质可得答案.
【详解】解:∵四边形ABCD中,ADBC轴,
∴点A与点D的纵坐标相同,点B与点C的纵坐标相同,
故A正确,BCD不正确,
故选:A.
【点睛】此题考查了平行四边形的性质,平行于坐标轴的点的坐标特点,正确理解平行四边形的性质是解题的关键.
8.A
【分析】根据平面直角坐标系中,在y轴上的点的坐标特点即可求解.
【详解】解:∵点在y轴上,
∴横坐标,则,
∴点P的坐标是(0,-4),
故选:A.
【点睛】本题考查了坐标轴上点的坐标特点,熟记在x轴上的点,纵坐标等于0;在y轴上的点,横坐标等于0是解题的关键.
9.A
【详解】解:∵线段CD是由线段AB平移得到的,
而点A( 1,4)的对应点为C(4,7),
∴由A平移到C点的横坐标增加5,纵坐标增加3,
则点B( 4, 1)的对应点D的坐标为(1,2).
故选:A
10.D
【分析】根据点的位置确定应该有方向以及距离,进而利用图象得出即可.
【详解】解:如图,
由图可知:∠AOB=90°-50°=40°,OA=4km,
∴点A在点O北偏东40°方向上4km处.
故选:D.
【点睛】此题主要考查了点的坐标确定位置,注意方向角的确定方法.
11.(3,3)或(6,-6)
【分析】由点到两坐标轴的距离相等可得出,求出a的值即可.
【详解】解:点坐标为,且点到两坐标轴的距离相等,
,
或,
或
∴或
解得:,.
当时,,
点M(3,3),
当时,,
∴点M(6,-6).
故答案为(3,3)或(6,-6).
【点睛】本题考查了点的坐标的知识,一元一次方程,解答关键在于得出,注意不要漏解.
12.
【分析】根据平面直角坐标系中,轴上的点的横坐标为0建立方程,解方程即可得.
【详解】解:点在轴上,
,
解得,
故答案为:.
【点睛】本题考查了点坐标,熟练掌握轴上的点的横坐标为0是解题关键.
13.或/(-4,8)或(-4,-2)
【分析】根据平行于y轴的直线上的点的横坐标相同求出点B的横坐标,再分点B在点A的上方与下方两种情况列式求出点B的纵坐标,即可得解.
【详解】解:∵AB∥y轴,
∴A、B两点的横坐标相同为-4,
又∵AB=5
∴B点纵坐标为:3+5=8,或3-5=-2,
∴B点的坐标为:(-4,8)或(-4,-2);
故答案为:(-4,8)或(-4,-2).
【点睛】本题考查了坐标与图形性质,主要利用了平行于y轴的直线上的点的横坐标相同,难点在于要分情况讨论.
14.(2022,0)
【分析】由,,,……点的横坐标依次是1、2、3、4、……、n,纵坐标依次是2、0、-2、0、2、0、-2、……,四个一循环,继而求得答案.
【详解】解:观察图形可知, 点,,,……的横坐标依次是1、2、3、4、……、n,
纵坐标依次是2、0、-2、0、2、0、-2、……,四个一循环,
2022÷4=505……2,
故点A2022坐标是(2022,0).
故答案为(2022,0).
【点睛】本题考查了规律型:点的坐标,学生的观察图形的能力和理解能力,解题的关键是根据图形中点的坐标得出规律.
15.
【分析】根据定在第四象限得出不等式组,再求出不等式组的解集即可.
【详解】解:∵点点在第四象限,
∴,
解得:,
即的取值范围是:,
故答案为:.
【点睛】此题主要考查了点的坐标与解一元一次不等式组,能得出关于的不等式组是解此题的关键.
16.
【分析】直接利用已知点坐标得出原点位置,进而得出答案.
【详解】解:如图,根据体育馆的坐标为,科技馆的坐标为,确定坐标原点如下:
故答案为:
【点睛】本题主要考查了坐标确定位置,正确得出原点位置是解题关键.
17.(1)见解析
(2)
(3)或
【分析】(1)依据点,,,即可描出A,B,C三点;
(2)根据三角形的面积公式求解;
(3)设点,根据三角形面积公式求解.
(1)
解:画出正确的坐标系如下:
(2)
解:∵点,,
∴点A,B到x轴的距离为其纵坐标的绝对值,即都为3,
∴轴,
∴.
作于点,则,如图,
∴的面积为:.
(3)
解:设点,
∴,
∴,
∴或,
∴点的坐标为或.
【点晴】本题主要考查了坐标与图形,三角形面积,画出图形是解答关键.
18.(1)(4,6);(2)点P的坐标为(4,4);(3) 当t=s或s时,点P到x轴的距离为5个单位长度.
【分析】(1)根据,,且四边形为长方形即可推出点坐标;
(2)当点移动时,求出点移动的路程即可根据点移动的速度找到点的坐标;
(3)分两种情况讨论点所在位置,即或时,分别找到移动的距离即可求出时间.
【详解】解:(1),,且四边形为长方形,
,,
点的坐标,
故答案为:;
(2)当点移动时,点移动的路程为:,
即,
,
,
故此时点坐标为;
(3)①当点第一次距轴5个单位长度时,,
此时点移动的距离:,
点每秒移动2个单位长度,
,
故;
②当点第二次距轴5个单位长度时,,
此时点移动的距离:,
点每秒移动2个单位长度,
,
故;
综上所述,在移动过程中,当点到轴的距离为5个单位长度时,移动的时间为s或s.
【点睛】本题属于四边形综合题,考查矩形的相关性质以及平面直角坐标系中坐标的变换,熟练掌握矩形的基本性质,数形结合,分类讨论是解题的关键.
19.(1), 49,
(2)或
【分析】(1)点的坐标为,结合平移方式可得C的坐标,由轴可得B的坐标,再利用割补法求解四边形的面积即可;
(2)设点 则 再利用面积公式列方程即可.
(1)
解:∵点的坐标为,将点向左移动7个单位长度,再向上移动2个单位长度至点,轴于点.
∴,
如图,过作轴于 则
∴四边形的面积=三角形OQC面积+梯形ABQC的面积
故答案为:,49,
(2)
设点 则
∵
解得:
或
【点睛】本题考查的是坐标与图形,由平移方式确定点的坐标,利用割补法求解图形的面积,掌握“平移的性质及点平移的坐标变化规律”是解本题的关键.
20.(1)见解析,、、
(2)11
【分析】(1)根据平移的规律得到A1,B1,C1点,再顺次连接即可;根据A1,B1,C1在坐标系中的位置写出各点坐标即可;
(2)根据图形的面积的和差求出△ABC的面积即可.
(1)
解:如图所示,
、、;
(2)
解:.
【点睛】本题考查了利用平移变换作图,利用平移变换作图,熟练掌握网格结构,准确找出对应点的位置是解题的关键.
21.(1)3
(2)见解析,D(0,0),E(2,2),F(3,0)
【分析】(1)首先根据A、B、C的坐标可得,,AC=3,AC边上的高为2,再根据三角形的面积公式,即可求得;
(2)根据点P,经平移后对应点为Q,即可得平移的方向及距离,据此即可解答.
(1)
解: A(,),C(0,),
,AC=3,AC边上的高为2,
△ABC的面积为:;
(2)
解:点P,经平移后对应点为Q,
点P向右平移了3个单位长度,向上平移了2个单位长度,
将△ABC向右平移3个单位长度,再向上平移2个单位长度得到△DEF,
点A、B、C 的对应点D、E、F的坐标分别为D(0,0),E(2,2),F(3,0),
画图如下:
【点睛】本题考查了坐标与图形,平移规律的探究,熟练掌握和运用平移规律的探究方法是解决本题的关键.
一、单选题
1.(2022春·天津河西·七年级统考期末)在平面直角坐标系中,点,,,若轴,则线段BC的最小值及此时点C的坐标分别为( )
A.3, B.10, C.1, D.6,
2.(2022春·天津南开·七年级统考期末)若点M在第四象限,且M到x轴的距离为1,到y轴的距离为2,则点M的坐标为( )
A.(1,-2) B.(2,1) C.(-2,1) D.(2,-1)
3.(2022春·天津西青·七年级统考期末)已知点是平面直角坐标系中轴上一点,且在轴的左侧,若点到轴的距离为3,则点的坐标为( )
A. B. C. D.
4.(2022春·天津河西·七年级统考期末)在平面直角坐标系中,点A(2,-3)所在的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.(2022春·天津南开·七年级统考期末)若M()满足,点M所在的象限是( )
A.第一、二象限 B.第一、三象限 C.第二、四象限 D.不能确定
6.(2022春·天津东丽·七年级统考期末)在平面直角坐标系中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”例如:三点坐标分别为,,,则“水平底”,“铅垂高”,“矩面积”若、,三点的“矩面积”为15,则t的值为( )
A.或7 B.或6 C.或7 D.或6
7.(2022春·天津津南·七年级统考期末)如图,在四边形ABCD中,ADBC轴,下列说法中正确的是( ).
A.点A与点D的纵坐标相同
B.点A与点B的横坐标相同
C.点A与点C的纵坐标相同
D.点B与点D的横坐标相同
8.(2022春·天津滨海新·七年级统考期末)若点在y轴上,则点P的坐标是( )
A. B. C. D.
9.(2022春·天津宝坻·七年级统考期末)已知线段CD是由线段AB平移得到的,点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为( )
A.(1,2) B.(2,9) C.(5,3) D.(–9,–4)
10.(2022春·天津东丽·七年级统考期末)点 A 的位置如图所示,则关于点 A 的位置下列说法中正确的是( )
A.距点处
B.北偏东 方向上处
C.在点北偏东 方向上处
D.在点北偏东 方向上距点处
二、填空题
11.(2022春·天津滨海新·七年级统考期末)已知点M坐标为且M点到两坐标轴的距离相等,则点的M坐标是________.
12.(2022春·天津南开·七年级统考期末)如果点在轴上,则________;
13.(2022春·天津宝坻·七年级统考期末)在平面直角坐标系中,点的坐标为.若线段轴,且的长为5,则点的坐标为_________.
14.(2022春·天津南开·七年级统考期末)如图,在平面直角坐标系中,,,,……根据这个规律,探究可得点的坐标是_____.
15.(2022春·天津红桥·七年级统考期末)在平面直角坐标系中,如果点在第四象限,则m的取值范围是______.
16.(2022春·天津西青·七年级统考期末)如图是某学校的部分平面示意图,在同一平面直角坐标系中,若体育馆的坐标为,科技馆的坐标为,则教学楼的坐标为______.
三、解答题
17.(2022春·天津宝坻·七年级统考期末)已知点,,.
(1)在平面直角坐标系中描出,,三点;
(2)求的面积;
(3)若点在轴上,当的面积为6时,请直接写出点的坐标.
18.(2022春·天津河西·七年级统考期末)如图,在平面直角坐标系中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形的边逆时针移动一周(即:沿着O→A→B→C→O的路线移动).
(1)点B的坐标为______;
(2)当点P移动4s时,求出点P的坐标;
(3)在移动过程中,当点P到轴的距离为5个单位长度时,求点P移动的时间t.
19.(2022春·天津西青·七年级统考期末)如图,在平面直角坐标系中,点的坐标为,轴于点.将点向左移动7个单位长度,再向上移动2个单位长度至点,连接,.
(1)点的坐标为______,点的坐标为______,四边形的面积为______.
(2)在轴上是否存在一点,使得三角形的面积是四边形面积的?若存在,请求出点的坐标;若不存在,请说明理由.
20.(2022春·天津河西·七年级统考期末)如图,在平面直角坐标系中,的顶点都在网格点上,每个小正方形边长为1个单位长度.
(1)将向右平移5个单位,再向下平移2个单位得到,画出图形,并写出各顶点坐标;
(2)求的面积.
21.(2022春·天津津南·七年级统考期末)如图,点A(,),点B(,0),点C(0,).
(1)求△ABC的面积.
(2)图中△ABC内一点P,经平移后对应点为Q,将△ABC作同样的平移得到△DEF,画出△DEF,并写出点A、B、C 的对应点D、E、F的坐标.
参考答案:
1.A
【分析】根据坐标的定义可求得y值,根据线段BC最小,确定BC⊥AC,垂足为点C,进一步求得BC的最小值和点C的坐标.
【详解】解:依题意可得:
∵AC∥x轴,A(-3,2)
∴y=2,
根据垂线段最短,当BC⊥AC于点C时,
点B到AC的距离最短,即BC的最小值=5-2=3,
此时点C的坐标为(3,2),
故选:A.
【点睛】本题考查已知点求坐标及如何根据坐标描点,正确画图即可求解.
2.D
【分析】先判断出点的横、纵坐标的符号,再根据点到轴、轴的距离即可得.
【详解】解:点在第四象限,
点的横坐标为正数,纵坐标为负数,
点到轴的距离为1,到轴的距离为2,
点的纵坐标为,横坐标为2,
即,
故选:D.
【点睛】本题考查了点坐标,熟练掌握各象限内的点坐标的符号规律是解题关键.
3.B
【分析】根据x轴上点的纵坐标为0,到y轴的距离等于横坐标的绝对值解答.
【详解】解:∵点P在x轴上,且在轴的左侧,到y轴的距离为3,
∴点P的坐标为(-3,0).
故选:B.
【点睛】本题考查了点的坐标,熟记x轴上点的纵坐标为0,到y轴的距离等于横坐标的绝对值是解题的关键.
4.D
【分析】根据平面直角坐标系中,各象限内的点坐标的符号规律即可得.
【详解】解:点的横坐标为,纵坐标为,
点所在的象限为第四象限,
故选:D.
【点睛】本题考查了点所在的象限,熟练掌握平面直角坐标系中,各象限内的点坐标的符号规律是解题关键.
5.B
【分析】由条件可得则同号,从而可得答案.
【详解】解:∵,
∴同号,
∴M()在第一或第三象限,
故选B
【点睛】本题考查了平面直角坐标系内点的坐标问题,求出x、y同号是解题的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).
6.D
【分析】根据题意可以求得a的值,然后再对t进行讨论,即可求得t的值.
【详解】解:由题意得:
“水平底”为:,
当时,,
则,
解得:;
当时,,
故此种情况不符合题意;
当时,,
则,
解得:.
故选:D.
【点睛】本题考查坐标与图形的性质,解答本题的关键是明确题目中的新定义,利用新定义解答问题.
7.A
【分析】根据平行四边形的性质可得答案.
【详解】解:∵四边形ABCD中,ADBC轴,
∴点A与点D的纵坐标相同,点B与点C的纵坐标相同,
故A正确,BCD不正确,
故选:A.
【点睛】此题考查了平行四边形的性质,平行于坐标轴的点的坐标特点,正确理解平行四边形的性质是解题的关键.
8.A
【分析】根据平面直角坐标系中,在y轴上的点的坐标特点即可求解.
【详解】解:∵点在y轴上,
∴横坐标,则,
∴点P的坐标是(0,-4),
故选:A.
【点睛】本题考查了坐标轴上点的坐标特点,熟记在x轴上的点,纵坐标等于0;在y轴上的点,横坐标等于0是解题的关键.
9.A
【详解】解:∵线段CD是由线段AB平移得到的,
而点A( 1,4)的对应点为C(4,7),
∴由A平移到C点的横坐标增加5,纵坐标增加3,
则点B( 4, 1)的对应点D的坐标为(1,2).
故选:A
10.D
【分析】根据点的位置确定应该有方向以及距离,进而利用图象得出即可.
【详解】解:如图,
由图可知:∠AOB=90°-50°=40°,OA=4km,
∴点A在点O北偏东40°方向上4km处.
故选:D.
【点睛】此题主要考查了点的坐标确定位置,注意方向角的确定方法.
11.(3,3)或(6,-6)
【分析】由点到两坐标轴的距离相等可得出,求出a的值即可.
【详解】解:点坐标为,且点到两坐标轴的距离相等,
,
或,
或
∴或
解得:,.
当时,,
点M(3,3),
当时,,
∴点M(6,-6).
故答案为(3,3)或(6,-6).
【点睛】本题考查了点的坐标的知识,一元一次方程,解答关键在于得出,注意不要漏解.
12.
【分析】根据平面直角坐标系中,轴上的点的横坐标为0建立方程,解方程即可得.
【详解】解:点在轴上,
,
解得,
故答案为:.
【点睛】本题考查了点坐标,熟练掌握轴上的点的横坐标为0是解题关键.
13.或/(-4,8)或(-4,-2)
【分析】根据平行于y轴的直线上的点的横坐标相同求出点B的横坐标,再分点B在点A的上方与下方两种情况列式求出点B的纵坐标,即可得解.
【详解】解:∵AB∥y轴,
∴A、B两点的横坐标相同为-4,
又∵AB=5
∴B点纵坐标为:3+5=8,或3-5=-2,
∴B点的坐标为:(-4,8)或(-4,-2);
故答案为:(-4,8)或(-4,-2).
【点睛】本题考查了坐标与图形性质,主要利用了平行于y轴的直线上的点的横坐标相同,难点在于要分情况讨论.
14.(2022,0)
【分析】由,,,……点的横坐标依次是1、2、3、4、……、n,纵坐标依次是2、0、-2、0、2、0、-2、……,四个一循环,继而求得答案.
【详解】解:观察图形可知, 点,,,……的横坐标依次是1、2、3、4、……、n,
纵坐标依次是2、0、-2、0、2、0、-2、……,四个一循环,
2022÷4=505……2,
故点A2022坐标是(2022,0).
故答案为(2022,0).
【点睛】本题考查了规律型:点的坐标,学生的观察图形的能力和理解能力,解题的关键是根据图形中点的坐标得出规律.
15.
【分析】根据定在第四象限得出不等式组,再求出不等式组的解集即可.
【详解】解:∵点点在第四象限,
∴,
解得:,
即的取值范围是:,
故答案为:.
【点睛】此题主要考查了点的坐标与解一元一次不等式组,能得出关于的不等式组是解此题的关键.
16.
【分析】直接利用已知点坐标得出原点位置,进而得出答案.
【详解】解:如图,根据体育馆的坐标为,科技馆的坐标为,确定坐标原点如下:
故答案为:
【点睛】本题主要考查了坐标确定位置,正确得出原点位置是解题关键.
17.(1)见解析
(2)
(3)或
【分析】(1)依据点,,,即可描出A,B,C三点;
(2)根据三角形的面积公式求解;
(3)设点,根据三角形面积公式求解.
(1)
解:画出正确的坐标系如下:
(2)
解:∵点,,
∴点A,B到x轴的距离为其纵坐标的绝对值,即都为3,
∴轴,
∴.
作于点,则,如图,
∴的面积为:.
(3)
解:设点,
∴,
∴,
∴或,
∴点的坐标为或.
【点晴】本题主要考查了坐标与图形,三角形面积,画出图形是解答关键.
18.(1)(4,6);(2)点P的坐标为(4,4);(3) 当t=s或s时,点P到x轴的距离为5个单位长度.
【分析】(1)根据,,且四边形为长方形即可推出点坐标;
(2)当点移动时,求出点移动的路程即可根据点移动的速度找到点的坐标;
(3)分两种情况讨论点所在位置,即或时,分别找到移动的距离即可求出时间.
【详解】解:(1),,且四边形为长方形,
,,
点的坐标,
故答案为:;
(2)当点移动时,点移动的路程为:,
即,
,
,
故此时点坐标为;
(3)①当点第一次距轴5个单位长度时,,
此时点移动的距离:,
点每秒移动2个单位长度,
,
故;
②当点第二次距轴5个单位长度时,,
此时点移动的距离:,
点每秒移动2个单位长度,
,
故;
综上所述,在移动过程中,当点到轴的距离为5个单位长度时,移动的时间为s或s.
【点睛】本题属于四边形综合题,考查矩形的相关性质以及平面直角坐标系中坐标的变换,熟练掌握矩形的基本性质,数形结合,分类讨论是解题的关键.
19.(1), 49,
(2)或
【分析】(1)点的坐标为,结合平移方式可得C的坐标,由轴可得B的坐标,再利用割补法求解四边形的面积即可;
(2)设点 则 再利用面积公式列方程即可.
(1)
解:∵点的坐标为,将点向左移动7个单位长度,再向上移动2个单位长度至点,轴于点.
∴,
如图,过作轴于 则
∴四边形的面积=三角形OQC面积+梯形ABQC的面积
故答案为:,49,
(2)
设点 则
∵
解得:
或
【点睛】本题考查的是坐标与图形,由平移方式确定点的坐标,利用割补法求解图形的面积,掌握“平移的性质及点平移的坐标变化规律”是解本题的关键.
20.(1)见解析,、、
(2)11
【分析】(1)根据平移的规律得到A1,B1,C1点,再顺次连接即可;根据A1,B1,C1在坐标系中的位置写出各点坐标即可;
(2)根据图形的面积的和差求出△ABC的面积即可.
(1)
解:如图所示,
、、;
(2)
解:.
【点睛】本题考查了利用平移变换作图,利用平移变换作图,熟练掌握网格结构,准确找出对应点的位置是解题的关键.
21.(1)3
(2)见解析,D(0,0),E(2,2),F(3,0)
【分析】(1)首先根据A、B、C的坐标可得,,AC=3,AC边上的高为2,再根据三角形的面积公式,即可求得;
(2)根据点P,经平移后对应点为Q,即可得平移的方向及距离,据此即可解答.
(1)
解: A(,),C(0,),
,AC=3,AC边上的高为2,
△ABC的面积为:;
(2)
解:点P,经平移后对应点为Q,
点P向右平移了3个单位长度,向上平移了2个单位长度,
将△ABC向右平移3个单位长度,再向上平移2个单位长度得到△DEF,
点A、B、C 的对应点D、E、F的坐标分别为D(0,0),E(2,2),F(3,0),
画图如下:
【点睛】本题考查了坐标与图形,平移规律的探究,熟练掌握和运用平移规律的探究方法是解决本题的关键.
