第九章:不等式与不等式组练习题(含解析)2021-2022学年天津市七年级下学期人教版数学期末试题选编
文档属性
| 名称 | 第九章:不等式与不等式组练习题(含解析)2021-2022学年天津市七年级下学期人教版数学期末试题选编 |  | |
| 格式 | zip | ||
| 文件大小 | 468.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-30 13:54:56 | ||
图片预览



文档简介
第九章:不等式与不等式组
一、单选题
1.(2022春·天津宝坻·七年级统考期末)已知,下列不等式中,不正确的是( )
A. B. C. D.
2.(2022春·天津红桥·七年级统考期末)把不等式的解集在数轴上表示出来,则正确的是( )
A. B.
C. D.
3.(2022春·天津西青·七年级统考期末)苹果的进价是每千克2.5元,销售中估计有5%的苹果正常损耗,要想不亏本,则售价至少应定为每千克( )
A.元 B.元 C.元 D.5元
4.(2022春·天津红桥·七年级统考期末)若不等式组 有解,则m的取值范围是( ).
A. B. C. D.
5.(2022春·天津东丽·七年级统考期末)某种商品的进价为80元,出售时标价为120元,后来由于该商品积压,商店准备打折出售,但要保证利润率不低于5%,则至多可打几折?如果将该商品打x折销售,则下列不等式中能正确表示该商店的促销方式的是( )
A.120x≥80×5% B.120x﹣80≥80×5%
C.120×≥80×5% D.120×﹣80≥80×5%
6.(2022春·天津滨海新·七年级校考期末)已知4<m≤5,则关于x的不等式组的整数解的个数共有( )
A.2 B.3 C.4 D.5
二、填空题
7.(2022春·天津南开·七年级统考期末)若点M(﹣2,7﹣a)是第二象限的点,则a的取值范围是______.
8.(2022春·天津西青·七年级统考期末)当______时,式子的值大于的值.
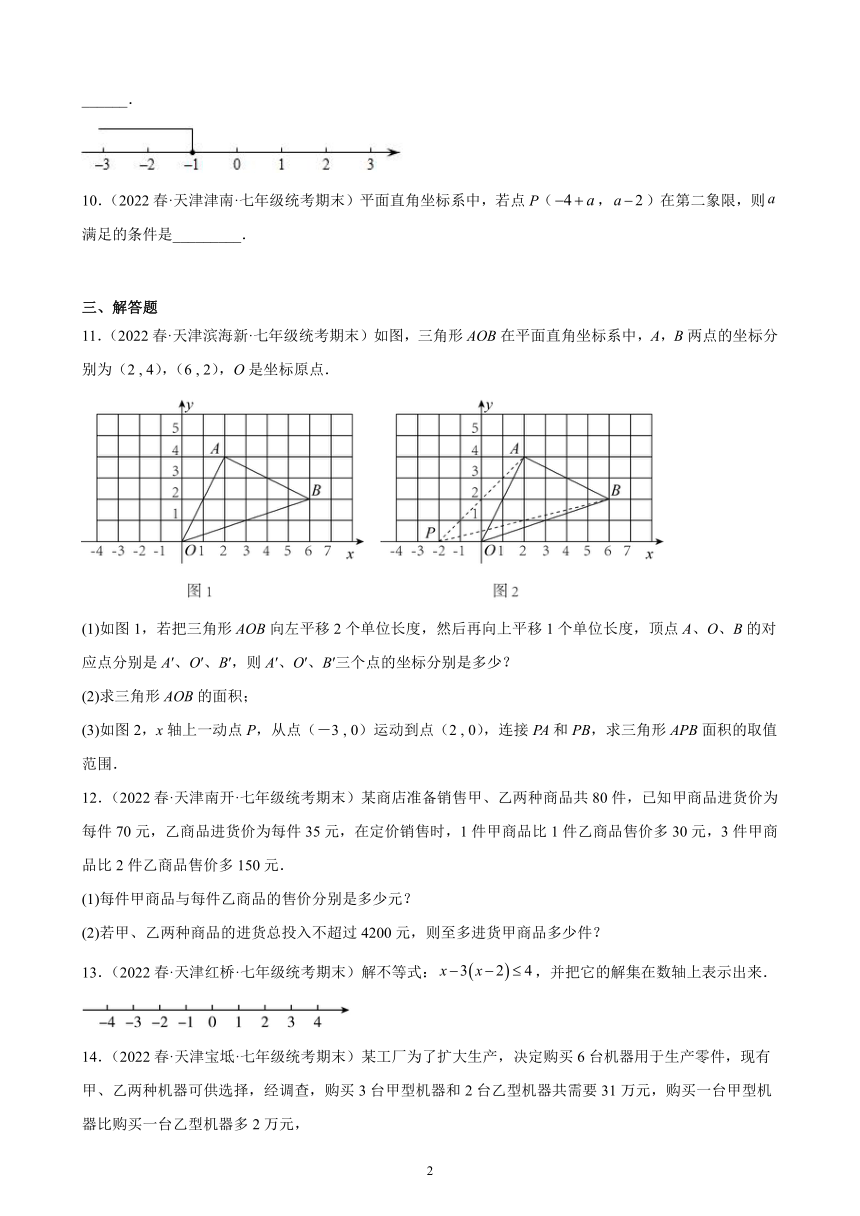
9.(2022春·天津滨海新·七年级校考期末)如果关于的不等式的解集如图所示,则的值是______.
10.(2022春·天津津南·七年级统考期末)平面直角坐标系中,若点P(,)在第二象限,则满足的条件是_________.
三、解答题
11.(2022春·天津滨海新·七年级统考期末)如图,三角形AOB在平面直角坐标系中,A,B两点的坐标分别为(2 , 4),(6 , 2),O是坐标原点.
(1)如图1,若把三角形AOB向左平移2个单位长度,然后再向上平移1个单位长度,顶点A、O、B的对应点分别是A′、O′、B′,则A′、O′、B′三个点的坐标分别是多少?
(2)求三角形AOB的面积;
(3)如图2,x轴上一动点P,从点(-3 , 0)运动到点(2 , 0),连接PA和PB,求三角形APB面积的取值范围.
12.(2022春·天津南开·七年级统考期末)某商店准备销售甲、乙两种商品共80件,已知甲商品进货价为每件70元,乙商品进货价为每件35元,在定价销售时,1件甲商品比1件乙商品售价多30元,3件甲商品比2件乙商品售价多150元.
(1)每件甲商品与每件乙商品的售价分别是多少元?
(2)若甲、乙两种商品的进货总投入不超过4200元,则至多进货甲商品多少件?
13.(2022春·天津红桥·七年级统考期末)解不等式:,并把它的解集在数轴上表示出来.
14.(2022春·天津宝坻·七年级统考期末)某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种机器可供选择,经调查,购买3台甲型机器和2台乙型机器共需要31万元,购买一台甲型机器比购买一台乙型机器多2万元,
(1)求甲、乙两型机器每台各多少万元
(2)如果该工厂买机器的预算资金不相过34万元,那么你认为该工厂至多购买甲型机器多少台
15.(2022春·天津东丽·七年级统考期末)为了保护环境,某企业决定购买10台污水处理设备.现有A、B两种型号的设备,其中每台的价格、月处理污水量及年消耗费如右表:经预算,该企业购买设备的资金不高于105万元.
A型 B型
价格(万元/台) 12 10
处理污水量(吨/月) 240 200
年消耗费(万元/台) 1 1
(1)请你设计该企业有几种购买方案;
(2)若企业每月产生的污水量为2040吨,为了节约资金,应选择哪种购买方案;
(3)在第(2)问的条件下,若每台设备的使用年限为10年,污水厂处理污水费为每吨10元,请你计算,该企业自己处理污水与将污水排到污水厂处理相比较,10年节约资金多少万元?(注:企业处理污水的费用包括购买设备的资金和消耗费)
16.(2022春·天津滨海新·七年级统考期末)某地面对形势异常严峻的新冠疫情,遵从党和国家部署,最大程度保障人民群众的健康,将所在区域划分为封控区、管控区和防范区. 现要将一批蔬菜运往封控区,已知用3辆A型车和1辆B型车装满蔬菜一次可运26吨;用1辆A型车和2辆B型车装满蔬菜一次可运22吨.
(1)求一辆A型车和一辆B型车装满蔬菜分别可运多少吨?
(2)若一辆A型车的租金是180元,一辆B型车的租金是220元,该地计划租用A型车和B型车共7辆,且租金不超过1400元,问最多可租用几辆B型车?
17.(2022春·天津红桥·七年级统考期末)求不等式组的整数解.
18.(2022春·天津滨海新·七年级校考期末)解不等式组
请结合题意填空,完成本题的解答.
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在数轴上表示出来:
(4)原不等式组的解集为 .
19.(2022春·天津宝坻·七年级统考期末)解下列不等式(组),并把解集表示在数轴上.
(1)
(2)
请结合题意填空,完成本题的解答
①解不等式①,得_______________;
②解不等式②,得_______________;
③把不等式①和②的解集在数轴上表示出来:
④原不等式组的解集为_______________.
20.(2022春·天津津南·七年级统考期末)解下列不等式(或不等式组),并把它们的解集在数轴上表示出来:
(1)
(2)≤
(3)
21.(2022春·天津西青·七年级统考期末)计算:
(1)解不等式;
(2)解不等式组.
请结合题意填空,完成本题的解答.
①解不等式①,得____________;
②解不等式②,得____________;
③把不等式①和②的解集在数轴上表示出来:
④原不等式组的解集为____________.
参考答案:
1.D
【分析】利用不等式的性质逐项判断求解.
【详解】解:A选项,不等式两边同时加4,不等号方向不变,故正确,不合题意;
B选项,不等式两边同时减3,不等号方向不变,故正确,不合题意;
C选项,不等式两边同时除以2,不等号方向不变,故正确,不合题意;
D选项,不等式两边同时乘以-2,不等号方向改变,故不正确,符合题意;
故选D.
【点睛】本题考查不等式的性质,解题的关键是牢记不等式的性质:不等式两边同时加上或减去一个数,不等号方向不变;不等式两边同时乘以或除以一个正数,不等号方向不变;不等式两边同时乘以或除以一个负数,不等号方向改变.
2.B
【分析】根据解一元一次不等式的步骤求出不等式的解集,再表示在数轴上即可.
【详解】解:,
移项得,
合并同类项得,
把未知数系数化为得,
表示在数轴上如下:
故选:B.
【点睛】本题考查解一元一次不等式,解题的关键是掌握解一元一次不等式的一般步骤.
3.A
【分析】设商家应把售价定为元,利用利润售价销售数量进价购进数量,结合不亏本,即可得出关于的一元一次不等式,解之取其中的最小值即可得出结论.
【详解】解:设商家应把售价定为元,
依题意得:,
解得:,
商家应把售价至少定为元.
故选:A.
【点睛】本题考查了一元一次不等式的应用,解题的关键是根据各数量之间的关系,正确列出一元一次不等式.
4.B
【分析】根据不等式组有解,可得,即可求解.
【详解】解:∵不等式组有解,
∴.
故选:B
【点睛】本题主要考查了解一元一次不等式组,熟练掌握解不等式组解集的口诀:同大取大,同小取小大小小大中间找,大大小小找不到(无解)是解题的关键.
5.D
【分析】根据题意找到不等关系再代入对应的数据即可.
【详解】设该商品打x折销售,根据题意可得:
故选:D.
【点睛】本题考查列不等式,解题的关键是找到题目中的不等关系,再代入数据即可.
6.B
【分析】可先将不等式组求出解集,再通过m的取值范围确定不等式组的解集中的整数解的个数即可.
【详解】解:不等式组整理得:,解集为,
∵,
∴整数解为2,3,4,共3个,
故选:B.
【点睛】本题考查含参数的不等式,解题的关键是根据参数的范围来确定不等式组的解集.
7.a<7
【分析】根据第二象限的符号特点(-,+),建立不等式解答即可.
【详解】∵M(﹣2,7﹣a)是第二象限的点,
∴7-a>0,
解得 a<7,
故答案为:a<7.
【点睛】本题考查了坐标与象限,不等式的解法,根据点的位置,正确建立不等式求解是解题的关键.
8.
【分析】由式子的值大于可得到一个关于的不等式,解这个不等式即可.
【详解】解:不等式,先移项得,
,
系数化为1,得.
故答案为:.
【点睛】本题考查了不等式的求解,解题的关键是根据已知条件列出不等式,再根据不等式的性质解不等式.
9.
【分析】解不等式得出x≤,结合数轴知x≤-1,据此得出=-1,解之可得答案.
【详解】解:∵3x-a≤-1,
∴3x≤a-1,
则x≤, 由数轴知x≤-1,
∴ =-1, 解得a=-2,
故答案为:-2.
【点睛】本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.
10.2<<4/.
【分析】根据第二象限内,点的横坐标为负,纵坐标为正,即可求解.
【详解】解:∵点P(,)在第二象限,
∴,解得:.
故答案为:.
【点睛】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点,熟练掌握四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-)是解题的关键.
11.(1)
(2)三角形AOB的面积为10
(3)三角形PAB面积的取值范围是8≤S△PAB≤13
【分析】(1)根据平移规则即可求出坐标;
(2)利用割补法求面积即可;
(3)设点P(x,0),表示出三角形APB面积几何x的取值范围即可解题.
(1)
∵把三角形AOB向左平移2个单位长度,然后再向上平移1个单位长度,
∴相当于横坐标减2,纵坐标加1
∴;
(2)
过点A作y轴的垂线交y轴于点C,过点B作x轴的垂线交x轴于点E,两垂线交于点D,构成长方形COED,设其面积为S.
∴点C(0 , 4),点D(6 , 4),点E(6 , 0)
∴AC=2,AD=4,DB=2,BE=2,CO=4,OE=6.
∴
(3)
过点P作x轴的垂线与DC的延长线交于点M,由图可知DMPE为长方形,设其面积为.
设点P(x,0),则点M为(x,4),
∵-3≤ x ≤2,
∴-2≤ -x ≤3
∴8≤10-x≤13 ,
8≤S△PAB≤13.
【点睛】本题考查坐标与平移、坐标系中求面积,熟练利用割补法求面积是解题的关键.
12.(1)每件甲商品售价为90元,每件乙商品售价为60元
(2)至多进货甲商品40件
【分析】(1)设每件甲商品与每件乙商品的售价分别是元、元,根据“1件甲商品比1件乙商品售价多30元,3件甲商品比2件乙商品售价多150元”列出二元一次方程组求解即可;
(2)设进货甲商品件,则乙商品件,根据题意列出一元一次不等式求解即可.
【详解】(1)设每件甲商品与每件乙商品的售价分别是元、元,得
解得:
答:每件甲商品售价为90元,每件乙商品售价为60元.
(2)设进货甲商品件,则乙商品件,依题意得:
,
解得
因此,至多进货甲商品40件.
【点睛】本题考查了一元一次不等式及二元一次方程组的应用,解决本题的关键是读懂题意,找到符合题意的不等关系式及所求量的等量关系.
13.,数轴见解析
【分析】先根据不等式的性质求出不等式的解集,再把不等式的解集在数轴上表示出来即可.
【详解】解:,
,
,
,
,
在数轴上表示为:
【点睛】本题考查了解一元一次不等式和在数轴上表示不等式的解集,能根据不等式的性质求出不等式的解集是解此题的关键.
14.(1)甲机器每台7万元,乙机器每台5万元
(2)该工厂至多购买甲型机器2台
【分析】(1)设甲机器每台x万元,乙机器每台y万元,根据等量关系式3台甲型机器+2台乙型机器=31万元,一台甲型机器-一台乙型机器=2万元,列出方程组,解方程组即可;
(2)设该工厂购买甲型机器m台,则购买乙型机器台,根据不等关系式甲型机器花费+乙型机器花费≤34万元,列出不等式,解不等式即可.
(1)
解:设甲机器每台x万元,乙机器每台y万元,根据题意得:
,
解得:,
答:甲机器每台7万元,乙机器每台5万元.
(2)
设该工厂购买甲型机器m台,则购买乙型机器台,根据题意得:
,
解得:,
答:该工厂至多购买甲型机器2台.
【点睛】本题主要考查了二元一次方程组的应用和一元一次不等式的应用,根据题意找出等量关系式,或不等关系式,是解题的关键.
15.(1)共有三种购买方案,A、B两种型号的设备分别为0台、10台或1台、9台或2台、8台;(2)A、B两种型号的设备分别1台、9台;(3)10年节约资金42.8万元
【分析】(1)设购买污水处理设备A型x台,则B型(10-x)台,根据“该企业购买设备的资金不高于105万元”即可列不等式求解,x的值取整数;
(2)先根据“企业每月产生的污水量为2040吨”列不等式求解,再根据x的值选出最佳方案;
(3)首先计算出企业自己处理污水的总资金,再计算出污水排到污水厂处理的费用,相比较即可判断.
【详解】(1)设购买污水处理设备A型x台,
则B型(10-x)台.
12x+10(10-x)≤105,
解得x≤2.5.
∵x取非负整数,∴x可取0,1,2.
有三种购买方案:购A型0台、B型10台;A型1台,B型9台;A型2台,B型8台;
(2)240x+200(10-x)≥2040,
解得x≥1,
所以x为1或2.
当x=1时,购买资金为:12×1+10×9=102(万元);
当x=2时,购买资金为12×2+10×8=104(万元),
所以为了节约资金,应选购A型1台,B型9台;
(3)10年企业自己处理污水的总资金为:
102+1×10+9×10=202(万元),
若将污水排到污水厂处理:
2040×12×10×10=2448000(元)=244.8(万元).
节约资金:244.8-202=42.8(万元).
【点睛】本题了不等式的应用——方案选择,方案问题是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.
16.(1)一辆A型车装满蔬菜可运6吨,一辆B型车装满蔬菜可运8吨
(2)最多可租用3辆B型车
【分析】(1)根据题意分别设A型车、B型车的装载量,根据题意列出二元一次方程组就,解方程组即可.
(2)根据A型车、B型车的数量关系设未知数,再根据租金关系建立不等式,然后根据实际问题的要求取合适的值.
(1)
设一辆A型车装满蔬菜可运x吨,一辆B型车装满蔬菜可运 y吨:
由题意得
解得 .
一辆A型车装满蔬菜可运6吨,一辆B型车装满蔬菜可运8吨.
(2)
设可租用m辆B型车,则A型车需(7-m)辆:
由题意得180(7-m)+220m≤1400,
解得:m ≤ .
∵m为整数
∴m=3
∴最多可租用3辆B型车.
【点睛】本题考查二元一次方程组和一元一次不等式的实际应用,根据题中所给的数量关系建立正确的方程是解决本题的关键.
17.0,1,2,3.
【分析】首先解每个不等式,两个不等式的公共部分就是不等式组的解集,然后确定解集中的整数解即可.
【详解】解析:
解不等式组①得:
解不等式组②得:
故不等式组解集为:,
整数解为:0,1,2,3.
【点睛】本题考查了一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.
18.(1)
(2)
(3)见解析
(4)
【分析】(1)根据不等式的性质解不等式即可;
(2)根据不等式的性质解不等式即可;
(3)在数轴上表示出两不等式的解集范围;
(4)确定两不等式解集的公共部分;
【详解】(1)解:解不等式①,得,;
(2)解:解不等式②,得;
(3)解:不等式①和②的解集在数轴上表示:
(4)解:原不等式组的解集为:;
【点睛】本题考查了不等式组的解法,掌握不等式组解集的确定方法是解题关键.
19.(1);解集表示在数轴上见解析
(2)①;②;③见解析;④
【分析】(1)先去括号,然后移项合并同类项,最后将系数化为1,并把解集表示在数轴上即可;
(2)先求出两个不等式的解集,然后再求出不等式组的解集,最后把解集表示在数轴上即可.
【详解】(1)解:
去括号得:,
移项合并同类项得:,
未知数系数化为1得:,
把不等式的解集表示在数轴上,如图所示:
(2)
①解不等式①,得;
②解不等式②,得;
③把不等式①和②的解集在数轴上表示出来:
④原不等式组的解集为.
故答案为:①;②;③见解析;④.
【点睛】本题主要考查了解不等式或不等式组,解题的关键是熟练掌握解不等式的一般步骤,注意不等式两边同乘或除一个相同的负数时,不等号方向改变.
20.(1);数轴见解析
(2);数轴见解析
(3);数轴见解析
【分析】(1)移项合并即可求得不等式的解集,再将解集在数轴上表示即可求解.
(2)先去分母,再去括号合并即可求得不等式的解集,再将解集在数轴上表示即可求解.
(3)根据求不等式的解集的方法分别求出不等式的解集,再根据找不等式组的解集的规律得出不等式组的解集,再将解集在数轴上表示即可求解.
(1)
解:不等式,
移项合并得:,
∴原不等式的解集为:,
原不等式的解集在数轴上表示为:
(2)
不等式≤,
去分母得,
去括号得,
移项合并得,
∴原不等式的解集为:,
原不等式的解集在数轴上表示为:
(3)
不等式,
去括号得,
解得,
不等式,
去分母得,
去括号得,
移项合并得,
∴原不等式组的解集为:,
原不等式组的解集在数轴上表示为:
【点睛】本题考查了解不等式和不等式组,并把解集在数轴上表示,熟练掌握不等式的解法及找不等式组的解集的规律,把解集在数轴上表示的方法是解题的关键.
21.(1)
(2);;画图见解析;
【分析】(1)先移项,再合并同类项,最后把未知数的系数化为“1”,即可得到答案;
(2)分别解不等式组中的两个不等式,再利用数轴确定解集的公共部分,从而可得答案.
【详解】(1)解:
移项可得:
解得:
(2)
①解不等式①,得;
②解不等式②,得 ;
③把不等式①和②的解集在数轴上表示出来:
④原不等式组的解集为.
【点睛】本题考查的是一元一次不等式的解法,一元一次不等式组的解法,掌握“解一元一次不等式组的方法与步骤”是解本题的关键.
一、单选题
1.(2022春·天津宝坻·七年级统考期末)已知,下列不等式中,不正确的是( )
A. B. C. D.
2.(2022春·天津红桥·七年级统考期末)把不等式的解集在数轴上表示出来,则正确的是( )
A. B.
C. D.
3.(2022春·天津西青·七年级统考期末)苹果的进价是每千克2.5元,销售中估计有5%的苹果正常损耗,要想不亏本,则售价至少应定为每千克( )
A.元 B.元 C.元 D.5元
4.(2022春·天津红桥·七年级统考期末)若不等式组 有解,则m的取值范围是( ).
A. B. C. D.
5.(2022春·天津东丽·七年级统考期末)某种商品的进价为80元,出售时标价为120元,后来由于该商品积压,商店准备打折出售,但要保证利润率不低于5%,则至多可打几折?如果将该商品打x折销售,则下列不等式中能正确表示该商店的促销方式的是( )
A.120x≥80×5% B.120x﹣80≥80×5%
C.120×≥80×5% D.120×﹣80≥80×5%
6.(2022春·天津滨海新·七年级校考期末)已知4<m≤5,则关于x的不等式组的整数解的个数共有( )
A.2 B.3 C.4 D.5
二、填空题
7.(2022春·天津南开·七年级统考期末)若点M(﹣2,7﹣a)是第二象限的点,则a的取值范围是______.
8.(2022春·天津西青·七年级统考期末)当______时,式子的值大于的值.
9.(2022春·天津滨海新·七年级校考期末)如果关于的不等式的解集如图所示,则的值是______.
10.(2022春·天津津南·七年级统考期末)平面直角坐标系中,若点P(,)在第二象限,则满足的条件是_________.
三、解答题
11.(2022春·天津滨海新·七年级统考期末)如图,三角形AOB在平面直角坐标系中,A,B两点的坐标分别为(2 , 4),(6 , 2),O是坐标原点.
(1)如图1,若把三角形AOB向左平移2个单位长度,然后再向上平移1个单位长度,顶点A、O、B的对应点分别是A′、O′、B′,则A′、O′、B′三个点的坐标分别是多少?
(2)求三角形AOB的面积;
(3)如图2,x轴上一动点P,从点(-3 , 0)运动到点(2 , 0),连接PA和PB,求三角形APB面积的取值范围.
12.(2022春·天津南开·七年级统考期末)某商店准备销售甲、乙两种商品共80件,已知甲商品进货价为每件70元,乙商品进货价为每件35元,在定价销售时,1件甲商品比1件乙商品售价多30元,3件甲商品比2件乙商品售价多150元.
(1)每件甲商品与每件乙商品的售价分别是多少元?
(2)若甲、乙两种商品的进货总投入不超过4200元,则至多进货甲商品多少件?
13.(2022春·天津红桥·七年级统考期末)解不等式:,并把它的解集在数轴上表示出来.
14.(2022春·天津宝坻·七年级统考期末)某工厂为了扩大生产,决定购买6台机器用于生产零件,现有甲、乙两种机器可供选择,经调查,购买3台甲型机器和2台乙型机器共需要31万元,购买一台甲型机器比购买一台乙型机器多2万元,
(1)求甲、乙两型机器每台各多少万元
(2)如果该工厂买机器的预算资金不相过34万元,那么你认为该工厂至多购买甲型机器多少台
15.(2022春·天津东丽·七年级统考期末)为了保护环境,某企业决定购买10台污水处理设备.现有A、B两种型号的设备,其中每台的价格、月处理污水量及年消耗费如右表:经预算,该企业购买设备的资金不高于105万元.
A型 B型
价格(万元/台) 12 10
处理污水量(吨/月) 240 200
年消耗费(万元/台) 1 1
(1)请你设计该企业有几种购买方案;
(2)若企业每月产生的污水量为2040吨,为了节约资金,应选择哪种购买方案;
(3)在第(2)问的条件下,若每台设备的使用年限为10年,污水厂处理污水费为每吨10元,请你计算,该企业自己处理污水与将污水排到污水厂处理相比较,10年节约资金多少万元?(注:企业处理污水的费用包括购买设备的资金和消耗费)
16.(2022春·天津滨海新·七年级统考期末)某地面对形势异常严峻的新冠疫情,遵从党和国家部署,最大程度保障人民群众的健康,将所在区域划分为封控区、管控区和防范区. 现要将一批蔬菜运往封控区,已知用3辆A型车和1辆B型车装满蔬菜一次可运26吨;用1辆A型车和2辆B型车装满蔬菜一次可运22吨.
(1)求一辆A型车和一辆B型车装满蔬菜分别可运多少吨?
(2)若一辆A型车的租金是180元,一辆B型车的租金是220元,该地计划租用A型车和B型车共7辆,且租金不超过1400元,问最多可租用几辆B型车?
17.(2022春·天津红桥·七年级统考期末)求不等式组的整数解.
18.(2022春·天津滨海新·七年级校考期末)解不等式组
请结合题意填空,完成本题的解答.
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在数轴上表示出来:
(4)原不等式组的解集为 .
19.(2022春·天津宝坻·七年级统考期末)解下列不等式(组),并把解集表示在数轴上.
(1)
(2)
请结合题意填空,完成本题的解答
①解不等式①,得_______________;
②解不等式②,得_______________;
③把不等式①和②的解集在数轴上表示出来:
④原不等式组的解集为_______________.
20.(2022春·天津津南·七年级统考期末)解下列不等式(或不等式组),并把它们的解集在数轴上表示出来:
(1)
(2)≤
(3)
21.(2022春·天津西青·七年级统考期末)计算:
(1)解不等式;
(2)解不等式组.
请结合题意填空,完成本题的解答.
①解不等式①,得____________;
②解不等式②,得____________;
③把不等式①和②的解集在数轴上表示出来:
④原不等式组的解集为____________.
参考答案:
1.D
【分析】利用不等式的性质逐项判断求解.
【详解】解:A选项,不等式两边同时加4,不等号方向不变,故正确,不合题意;
B选项,不等式两边同时减3,不等号方向不变,故正确,不合题意;
C选项,不等式两边同时除以2,不等号方向不变,故正确,不合题意;
D选项,不等式两边同时乘以-2,不等号方向改变,故不正确,符合题意;
故选D.
【点睛】本题考查不等式的性质,解题的关键是牢记不等式的性质:不等式两边同时加上或减去一个数,不等号方向不变;不等式两边同时乘以或除以一个正数,不等号方向不变;不等式两边同时乘以或除以一个负数,不等号方向改变.
2.B
【分析】根据解一元一次不等式的步骤求出不等式的解集,再表示在数轴上即可.
【详解】解:,
移项得,
合并同类项得,
把未知数系数化为得,
表示在数轴上如下:
故选:B.
【点睛】本题考查解一元一次不等式,解题的关键是掌握解一元一次不等式的一般步骤.
3.A
【分析】设商家应把售价定为元,利用利润售价销售数量进价购进数量,结合不亏本,即可得出关于的一元一次不等式,解之取其中的最小值即可得出结论.
【详解】解:设商家应把售价定为元,
依题意得:,
解得:,
商家应把售价至少定为元.
故选:A.
【点睛】本题考查了一元一次不等式的应用,解题的关键是根据各数量之间的关系,正确列出一元一次不等式.
4.B
【分析】根据不等式组有解,可得,即可求解.
【详解】解:∵不等式组有解,
∴.
故选:B
【点睛】本题主要考查了解一元一次不等式组,熟练掌握解不等式组解集的口诀:同大取大,同小取小大小小大中间找,大大小小找不到(无解)是解题的关键.
5.D
【分析】根据题意找到不等关系再代入对应的数据即可.
【详解】设该商品打x折销售,根据题意可得:
故选:D.
【点睛】本题考查列不等式,解题的关键是找到题目中的不等关系,再代入数据即可.
6.B
【分析】可先将不等式组求出解集,再通过m的取值范围确定不等式组的解集中的整数解的个数即可.
【详解】解:不等式组整理得:,解集为,
∵,
∴整数解为2,3,4,共3个,
故选:B.
【点睛】本题考查含参数的不等式,解题的关键是根据参数的范围来确定不等式组的解集.
7.a<7
【分析】根据第二象限的符号特点(-,+),建立不等式解答即可.
【详解】∵M(﹣2,7﹣a)是第二象限的点,
∴7-a>0,
解得 a<7,
故答案为:a<7.
【点睛】本题考查了坐标与象限,不等式的解法,根据点的位置,正确建立不等式求解是解题的关键.
8.
【分析】由式子的值大于可得到一个关于的不等式,解这个不等式即可.
【详解】解:不等式,先移项得,
,
系数化为1,得.
故答案为:.
【点睛】本题考查了不等式的求解,解题的关键是根据已知条件列出不等式,再根据不等式的性质解不等式.
9.
【分析】解不等式得出x≤,结合数轴知x≤-1,据此得出=-1,解之可得答案.
【详解】解:∵3x-a≤-1,
∴3x≤a-1,
则x≤, 由数轴知x≤-1,
∴ =-1, 解得a=-2,
故答案为:-2.
【点睛】本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.
10.2<<4/.
【分析】根据第二象限内,点的横坐标为负,纵坐标为正,即可求解.
【详解】解:∵点P(,)在第二象限,
∴,解得:.
故答案为:.
【点睛】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点,熟练掌握四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-)是解题的关键.
11.(1)
(2)三角形AOB的面积为10
(3)三角形PAB面积的取值范围是8≤S△PAB≤13
【分析】(1)根据平移规则即可求出坐标;
(2)利用割补法求面积即可;
(3)设点P(x,0),表示出三角形APB面积几何x的取值范围即可解题.
(1)
∵把三角形AOB向左平移2个单位长度,然后再向上平移1个单位长度,
∴相当于横坐标减2,纵坐标加1
∴;
(2)
过点A作y轴的垂线交y轴于点C,过点B作x轴的垂线交x轴于点E,两垂线交于点D,构成长方形COED,设其面积为S.
∴点C(0 , 4),点D(6 , 4),点E(6 , 0)
∴AC=2,AD=4,DB=2,BE=2,CO=4,OE=6.
∴
(3)
过点P作x轴的垂线与DC的延长线交于点M,由图可知DMPE为长方形,设其面积为.
设点P(x,0),则点M为(x,4),
∵-3≤ x ≤2,
∴-2≤ -x ≤3
∴8≤10-x≤13 ,
8≤S△PAB≤13.
【点睛】本题考查坐标与平移、坐标系中求面积,熟练利用割补法求面积是解题的关键.
12.(1)每件甲商品售价为90元,每件乙商品售价为60元
(2)至多进货甲商品40件
【分析】(1)设每件甲商品与每件乙商品的售价分别是元、元,根据“1件甲商品比1件乙商品售价多30元,3件甲商品比2件乙商品售价多150元”列出二元一次方程组求解即可;
(2)设进货甲商品件,则乙商品件,根据题意列出一元一次不等式求解即可.
【详解】(1)设每件甲商品与每件乙商品的售价分别是元、元,得
解得:
答:每件甲商品售价为90元,每件乙商品售价为60元.
(2)设进货甲商品件,则乙商品件,依题意得:
,
解得
因此,至多进货甲商品40件.
【点睛】本题考查了一元一次不等式及二元一次方程组的应用,解决本题的关键是读懂题意,找到符合题意的不等关系式及所求量的等量关系.
13.,数轴见解析
【分析】先根据不等式的性质求出不等式的解集,再把不等式的解集在数轴上表示出来即可.
【详解】解:,
,
,
,
,
在数轴上表示为:
【点睛】本题考查了解一元一次不等式和在数轴上表示不等式的解集,能根据不等式的性质求出不等式的解集是解此题的关键.
14.(1)甲机器每台7万元,乙机器每台5万元
(2)该工厂至多购买甲型机器2台
【分析】(1)设甲机器每台x万元,乙机器每台y万元,根据等量关系式3台甲型机器+2台乙型机器=31万元,一台甲型机器-一台乙型机器=2万元,列出方程组,解方程组即可;
(2)设该工厂购买甲型机器m台,则购买乙型机器台,根据不等关系式甲型机器花费+乙型机器花费≤34万元,列出不等式,解不等式即可.
(1)
解:设甲机器每台x万元,乙机器每台y万元,根据题意得:
,
解得:,
答:甲机器每台7万元,乙机器每台5万元.
(2)
设该工厂购买甲型机器m台,则购买乙型机器台,根据题意得:
,
解得:,
答:该工厂至多购买甲型机器2台.
【点睛】本题主要考查了二元一次方程组的应用和一元一次不等式的应用,根据题意找出等量关系式,或不等关系式,是解题的关键.
15.(1)共有三种购买方案,A、B两种型号的设备分别为0台、10台或1台、9台或2台、8台;(2)A、B两种型号的设备分别1台、9台;(3)10年节约资金42.8万元
【分析】(1)设购买污水处理设备A型x台,则B型(10-x)台,根据“该企业购买设备的资金不高于105万元”即可列不等式求解,x的值取整数;
(2)先根据“企业每月产生的污水量为2040吨”列不等式求解,再根据x的值选出最佳方案;
(3)首先计算出企业自己处理污水的总资金,再计算出污水排到污水厂处理的费用,相比较即可判断.
【详解】(1)设购买污水处理设备A型x台,
则B型(10-x)台.
12x+10(10-x)≤105,
解得x≤2.5.
∵x取非负整数,∴x可取0,1,2.
有三种购买方案:购A型0台、B型10台;A型1台,B型9台;A型2台,B型8台;
(2)240x+200(10-x)≥2040,
解得x≥1,
所以x为1或2.
当x=1时,购买资金为:12×1+10×9=102(万元);
当x=2时,购买资金为12×2+10×8=104(万元),
所以为了节约资金,应选购A型1台,B型9台;
(3)10年企业自己处理污水的总资金为:
102+1×10+9×10=202(万元),
若将污水排到污水厂处理:
2040×12×10×10=2448000(元)=244.8(万元).
节约资金:244.8-202=42.8(万元).
【点睛】本题了不等式的应用——方案选择,方案问题是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.
16.(1)一辆A型车装满蔬菜可运6吨,一辆B型车装满蔬菜可运8吨
(2)最多可租用3辆B型车
【分析】(1)根据题意分别设A型车、B型车的装载量,根据题意列出二元一次方程组就,解方程组即可.
(2)根据A型车、B型车的数量关系设未知数,再根据租金关系建立不等式,然后根据实际问题的要求取合适的值.
(1)
设一辆A型车装满蔬菜可运x吨,一辆B型车装满蔬菜可运 y吨:
由题意得
解得 .
一辆A型车装满蔬菜可运6吨,一辆B型车装满蔬菜可运8吨.
(2)
设可租用m辆B型车,则A型车需(7-m)辆:
由题意得180(7-m)+220m≤1400,
解得:m ≤ .
∵m为整数
∴m=3
∴最多可租用3辆B型车.
【点睛】本题考查二元一次方程组和一元一次不等式的实际应用,根据题中所给的数量关系建立正确的方程是解决本题的关键.
17.0,1,2,3.
【分析】首先解每个不等式,两个不等式的公共部分就是不等式组的解集,然后确定解集中的整数解即可.
【详解】解析:
解不等式组①得:
解不等式组②得:
故不等式组解集为:,
整数解为:0,1,2,3.
【点睛】本题考查了一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.
18.(1)
(2)
(3)见解析
(4)
【分析】(1)根据不等式的性质解不等式即可;
(2)根据不等式的性质解不等式即可;
(3)在数轴上表示出两不等式的解集范围;
(4)确定两不等式解集的公共部分;
【详解】(1)解:解不等式①,得,;
(2)解:解不等式②,得;
(3)解:不等式①和②的解集在数轴上表示:
(4)解:原不等式组的解集为:;
【点睛】本题考查了不等式组的解法,掌握不等式组解集的确定方法是解题关键.
19.(1);解集表示在数轴上见解析
(2)①;②;③见解析;④
【分析】(1)先去括号,然后移项合并同类项,最后将系数化为1,并把解集表示在数轴上即可;
(2)先求出两个不等式的解集,然后再求出不等式组的解集,最后把解集表示在数轴上即可.
【详解】(1)解:
去括号得:,
移项合并同类项得:,
未知数系数化为1得:,
把不等式的解集表示在数轴上,如图所示:
(2)
①解不等式①,得;
②解不等式②,得;
③把不等式①和②的解集在数轴上表示出来:
④原不等式组的解集为.
故答案为:①;②;③见解析;④.
【点睛】本题主要考查了解不等式或不等式组,解题的关键是熟练掌握解不等式的一般步骤,注意不等式两边同乘或除一个相同的负数时,不等号方向改变.
20.(1);数轴见解析
(2);数轴见解析
(3);数轴见解析
【分析】(1)移项合并即可求得不等式的解集,再将解集在数轴上表示即可求解.
(2)先去分母,再去括号合并即可求得不等式的解集,再将解集在数轴上表示即可求解.
(3)根据求不等式的解集的方法分别求出不等式的解集,再根据找不等式组的解集的规律得出不等式组的解集,再将解集在数轴上表示即可求解.
(1)
解:不等式,
移项合并得:,
∴原不等式的解集为:,
原不等式的解集在数轴上表示为:
(2)
不等式≤,
去分母得,
去括号得,
移项合并得,
∴原不等式的解集为:,
原不等式的解集在数轴上表示为:
(3)
不等式,
去括号得,
解得,
不等式,
去分母得,
去括号得,
移项合并得,
∴原不等式组的解集为:,
原不等式组的解集在数轴上表示为:
【点睛】本题考查了解不等式和不等式组,并把解集在数轴上表示,熟练掌握不等式的解法及找不等式组的解集的规律,把解集在数轴上表示的方法是解题的关键.
21.(1)
(2);;画图见解析;
【分析】(1)先移项,再合并同类项,最后把未知数的系数化为“1”,即可得到答案;
(2)分别解不等式组中的两个不等式,再利用数轴确定解集的公共部分,从而可得答案.
【详解】(1)解:
移项可得:
解得:
(2)
①解不等式①,得;
②解不等式②,得 ;
③把不等式①和②的解集在数轴上表示出来:
④原不等式组的解集为.
【点睛】本题考查的是一元一次不等式的解法,一元一次不等式组的解法,掌握“解一元一次不等式组的方法与步骤”是解本题的关键.
