第19章解直角三角形19.2勾 股 定 理(第二课时)[下学期]
文档属性
| 名称 | 第19章解直角三角形19.2勾 股 定 理(第二课时)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 66.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-05-08 00:00:00 | ||
图片预览




文档简介
课件11张PPT。勾股定理习题课(2)问题回顾勾股定理的内容是什么?答:直角三角形的两条直角边的平方和等于斜边的平方.勾股定理揭示了直角三角形的三边之间的关系.1、在Rt△ABC中,斜边AB=2,则AB2+BC2+CA2= .
2、在Rt△ABC中,∠C=90°,AC=3,BC= ,则AB= .
3、在△ABC中, ∠ACB=90°,CD⊥AB于D,AC=6,BC=8,则AB= ,AD= .
4、一个直角三角形的三边长为3个连续的偶数,则他们分别为 .
5、等腰直角三角形的斜边长为2,他的面积为 .
6、若一直角三角形两直角边的比是3:4,斜边长是20,则此直角三角形的面积为 .
7、在Rt△ABC中,斜边AB上的高为CD,若AC=3,BC=4,则CD = .填空:8103.66、8、101962.48、如图, △ABC中,∠ACB=90°,AC=12,CB=5,AM=AC,BN=BC,则MN的长是 .49、在如图所示的图形中,所有的四边形都是正方形,
所有的三角形都是直角三角形,其中最大的正方形的
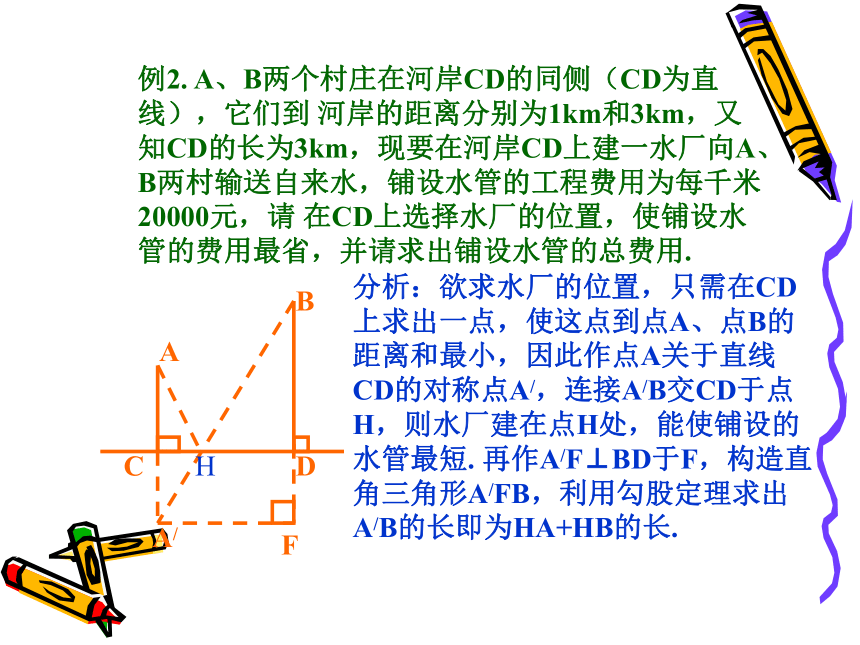
边长为7 cm,则正方形A、B、C、D的面积的和是 cm249例2. A、B两个村庄在河岸CD的同侧(CD为直线),它们到 河岸的距离分别为1km和3km,又知CD的长为3km,现要在河岸CD上建一水厂向A、B两村输送自来水,铺设水管的工程费用为每千米20000元,请 在CD上选择水厂的位置,使铺设水管的费用最省,并请求出铺设水管的总费用.AFA/H分析:欲求水厂的位置,只需在CD上求出一点,使这点到点A、点B的距离和最小,因此作点A关于直线CD的对称点A/,连接A/B交CD于点H,则水厂建在点H处,能使铺设的水管最短. 再作A/F⊥BD于F,构造直角三角形A/FB,利用勾股定理求出A/B的长即为HA+HB的长.例 3.在一棵树的10m高处有两只猴子,其中一只爬下树走向离树20m的池塘,而另一只爬到树顶后直扑池塘,如果两只猴子经过的距离相等,问这棵树有多高?解:如图,D为树顶,B处有两只猴子,则AB=10m,C为池塘,则AC=20m
设BD的长为x(m),则树高为(x+10)m
因为AC+AB=BD+DC,所以DC=20+10-x=30-x
在⊿ACD中,∠A=90°,所以AC2+AD2=DC2
故202+(10+x)2=(30-x)2 ,解得x=5
所以x+10=15,即树高15m例4.如图沿AE折叠矩形,点D恰好落在 BC边上的点F处,已知AB =8cm,BC = 10cm,求EC的长.解:∵点F、D关于AE对称 ∴ ΔAFE ≌ ΔAD E ∴ AF=AD ,EF =ED ∠AFE = ∠ ADE ∵四边形ABCD是矩形 ∴BC=AD AB =CD ∠C = ∠ ADE =900 又∵AB =8cm BC =10cm ∴ AF=10cm CD =8cm 在Rt Δ ABF中 BF=
∴FC =4cm 设EC =xcm 则DE=EF=(8-x)cm 在 Δ CFE 中,∵EF2=EC2+FC2 ∴ (8-x)2 = x2+42 解得x=3 答:EC的长为3cm.
1.在Rt⊿ABC中, ∠C=900 ,CD⊥AB于D,AD=1,BD=4,求AC的长。补充作业2.如图,在⊿ABC中, ∠C=90°,AD,BE分别是BC,AC边上的中线,AD=2 cm, BE=5cm, 求AB的长。(第2题)(第4题)3.已知在△ABC中,∠C=90°,∠A,∠B,∠C,的对边分别为a,b,c求a4+b4-c4+2a2b2的值.4.如图,已知长方体盒子的宽a=4m,长b=5m,高c=3m。一只聪明的小蚂蚁从顶点A处出发在长方体的表面上爬行,想尽快吃到在顶点B处的糖果,求小蚂蚁爬行的最短路径的长。5.如图,一张宽为3,长为4 的矩形纸片ABCD,沿对角线BD对折,点C落在点C’的位置,BC’交AD于E.求AE的长.ABCEC’6.在平静的湖面上,有一只荷花,高出水面1米,一阵风吹来,荷花吹到一边,花朵齐及水面.已知荷花移动的水平距离为2 米,求这里的水深是多少米?12(第5题)D(第6题)8.如图,已知长方体笼子的长a=4m,宽b=3m,高c=5m,笼内顶点A处有一猴子,“飞行”到顶点B处吃到香蕉,求小猴子“飞行”的最短距离是多?。EBCD(第7题)A(第8题)7.如图,在⊿ABC中, ∠C=90°,AC=BC,D是BC的中点,DE⊥AB于E,求证:AB2=16DE23.如图,正四棱柱的底面边长为5cm,侧棱长为8cm,一只蚂蚁欲从正四棱柱的底面上的点A沿棱柱侧面到点C1处吃食物,那么它需要爬行的最短路径是多少? 解:如下图,将四棱柱的侧面展开,连结AC1,∵AC=10cm,CC1=8cm(已知), 老师提示:对于空间图形需要动手操作,将其转化为平面图形来解决. 答:蚂蚁需要爬行的最短路径是 cm.
2、在Rt△ABC中,∠C=90°,AC=3,BC= ,则AB= .
3、在△ABC中, ∠ACB=90°,CD⊥AB于D,AC=6,BC=8,则AB= ,AD= .
4、一个直角三角形的三边长为3个连续的偶数,则他们分别为 .
5、等腰直角三角形的斜边长为2,他的面积为 .
6、若一直角三角形两直角边的比是3:4,斜边长是20,则此直角三角形的面积为 .
7、在Rt△ABC中,斜边AB上的高为CD,若AC=3,BC=4,则CD = .填空:8103.66、8、101962.48、如图, △ABC中,∠ACB=90°,AC=12,CB=5,AM=AC,BN=BC,则MN的长是 .49、在如图所示的图形中,所有的四边形都是正方形,
所有的三角形都是直角三角形,其中最大的正方形的
边长为7 cm,则正方形A、B、C、D的面积的和是 cm249例2. A、B两个村庄在河岸CD的同侧(CD为直线),它们到 河岸的距离分别为1km和3km,又知CD的长为3km,现要在河岸CD上建一水厂向A、B两村输送自来水,铺设水管的工程费用为每千米20000元,请 在CD上选择水厂的位置,使铺设水管的费用最省,并请求出铺设水管的总费用.AFA/H分析:欲求水厂的位置,只需在CD上求出一点,使这点到点A、点B的距离和最小,因此作点A关于直线CD的对称点A/,连接A/B交CD于点H,则水厂建在点H处,能使铺设的水管最短. 再作A/F⊥BD于F,构造直角三角形A/FB,利用勾股定理求出A/B的长即为HA+HB的长.例 3.在一棵树的10m高处有两只猴子,其中一只爬下树走向离树20m的池塘,而另一只爬到树顶后直扑池塘,如果两只猴子经过的距离相等,问这棵树有多高?解:如图,D为树顶,B处有两只猴子,则AB=10m,C为池塘,则AC=20m
设BD的长为x(m),则树高为(x+10)m
因为AC+AB=BD+DC,所以DC=20+10-x=30-x
在⊿ACD中,∠A=90°,所以AC2+AD2=DC2
故202+(10+x)2=(30-x)2 ,解得x=5
所以x+10=15,即树高15m例4.如图沿AE折叠矩形,点D恰好落在 BC边上的点F处,已知AB =8cm,BC = 10cm,求EC的长.解:∵点F、D关于AE对称 ∴ ΔAFE ≌ ΔAD E ∴ AF=AD ,EF =ED ∠AFE = ∠ ADE ∵四边形ABCD是矩形 ∴BC=AD AB =CD ∠C = ∠ ADE =900 又∵AB =8cm BC =10cm ∴ AF=10cm CD =8cm 在Rt Δ ABF中 BF=
∴FC =4cm 设EC =xcm 则DE=EF=(8-x)cm 在 Δ CFE 中,∵EF2=EC2+FC2 ∴ (8-x)2 = x2+42 解得x=3 答:EC的长为3cm.
1.在Rt⊿ABC中, ∠C=900 ,CD⊥AB于D,AD=1,BD=4,求AC的长。补充作业2.如图,在⊿ABC中, ∠C=90°,AD,BE分别是BC,AC边上的中线,AD=2 cm, BE=5cm, 求AB的长。(第2题)(第4题)3.已知在△ABC中,∠C=90°,∠A,∠B,∠C,的对边分别为a,b,c求a4+b4-c4+2a2b2的值.4.如图,已知长方体盒子的宽a=4m,长b=5m,高c=3m。一只聪明的小蚂蚁从顶点A处出发在长方体的表面上爬行,想尽快吃到在顶点B处的糖果,求小蚂蚁爬行的最短路径的长。5.如图,一张宽为3,长为4 的矩形纸片ABCD,沿对角线BD对折,点C落在点C’的位置,BC’交AD于E.求AE的长.ABCEC’6.在平静的湖面上,有一只荷花,高出水面1米,一阵风吹来,荷花吹到一边,花朵齐及水面.已知荷花移动的水平距离为2 米,求这里的水深是多少米?12(第5题)D(第6题)8.如图,已知长方体笼子的长a=4m,宽b=3m,高c=5m,笼内顶点A处有一猴子,“飞行”到顶点B处吃到香蕉,求小猴子“飞行”的最短距离是多?。EBCD(第7题)A(第8题)7.如图,在⊿ABC中, ∠C=90°,AC=BC,D是BC的中点,DE⊥AB于E,求证:AB2=16DE23.如图,正四棱柱的底面边长为5cm,侧棱长为8cm,一只蚂蚁欲从正四棱柱的底面上的点A沿棱柱侧面到点C1处吃食物,那么它需要爬行的最短路径是多少? 解:如下图,将四棱柱的侧面展开,连结AC1,∵AC=10cm,CC1=8cm(已知), 老师提示:对于空间图形需要动手操作,将其转化为平面图形来解决. 答:蚂蚁需要爬行的最短路径是 cm.
