第二十章:数据的分析练习题(含解析)2021-2022学年天津市各地八年级下学期人教版数学期末试题选编
文档属性
| 名称 | 第二十章:数据的分析练习题(含解析)2021-2022学年天津市各地八年级下学期人教版数学期末试题选编 |

|
|
| 格式 | zip | ||
| 文件大小 | 432.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-30 00:00:00 | ||
图片预览



文档简介
第二十章:数据的分析
一、单选题
1.(2022春·天津西青·八年级统考期末)一组数据:5,7,6,3,4的平均数是( )
A.5 B.6 C.4 D.8
2.(2022春·天津河北·八年级统考期末)-3,-2,4,x,5,8这六个数的平均数是3,则x的值为( )
A.4 B.5 C.6 D.7
3.(2022春·天津滨海新·八年级统考期末)已知一组数据,,3,,,的平均数是,那么这组数据的中位数是( )
A.1 B. C. D.
(2022春·天津西青·八年级统考期末)某校10名学生参加“交通安全”知识测试,他们得分情况如表中所示,则这10名学生所得分数的众数和中位数分别是( )
A.95和85 B.90和85 C.90和87.5 D.85和87.5
5.(2022春·天津津南·八年级统考期末)一家鞋店在一段时间内销售某种运动鞋30双,各种尺码鞋的销量如下表所示,对于进货,商家最关注的是由鞋码组成的这组数据的( )
尺码/cm 24 24.5 25 25.5 26 26.5 27
销售量/双 1 2 5 11 7 3 1
A.平均数 B.中位数 C.众数 D.方差
6.(2022春·天津东丽·八年级统考期末)歌唱比赛有二十位评委给选手打分,统计每位选手得分时,会去掉一个最高分和一个最低分,这样做,肯定不会对所有评委打分的哪一个统计量产生影响( )
A.平均分 B.众数 C.中位数 D.极差
7.(2022春·天津南开·八年级统考期末)2022年北京-张家口举办了冬季奥运会,很多学校也开设了相关的课程.下表记录了某校4名同学短道速滑选拔赛成绩的平均数与方差
队员1 队员2 队员3 队员4
平均数(秒) 51 50 51 50
方差(秒2) 3.5 3.5 14.5 14.5
据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A.队员1 B.队员2 C.队员3 D.队员4
8.(2022春·天津北辰·八年级统考期末)某跳远队准备选取一批队员参加比赛,要比较谁的成绩稳定,应选用的统计量是( )
A.平均数 B.众数 C.中位数 D.方差
9.(2022春·天津津南·八年级统考期末)八年级⑴班与⑵班各选出10名学生进行英文打字比赛,通过对参赛学生每分钟输入的单词个数进行统计,两班成绩的平均数相同,⑴班成绩的方差为12.5,⑵班成绩的方差为11,由此可知( )
A.⑵班比⑴班的成绩稳定 B.⑴班比⑵班的成绩稳定
C.两个班的成绩一样稳定 D.无法确定哪班的成绩更稳定
二、填空题
10.(2022春·天津西青·八年级统考期末)某校规定:学生的数学学科学期综合成绩是由平时、期中和期末三项成绩按的比例计算所得,若某同学本学期数学学科的平时、期中和期末成绩分别是90分,90分和80分,则他本学期数学学期综合成绩是_______分.
11.(2022春·天津北辰·八年级统考期末)如表是某体校女子体操队队员的年龄分布:
年龄/岁 13 14 15 16
人数 8 6 2 1
则该体校女子体操队队员年龄的中位数是 _____岁.
12.(2022春·天津津南·八年级统考期末)某公司招聘,甲、乙两位候选人面试和笔试成绩如表所示. 若面试与笔试成绩按6和4的权计算每人的平均成绩,从两人的成绩看,公司录取的是__________(填“甲” 或“乙”).
候选人 面试 笔试
甲 92 84
乙 90 86
13.(2022春·天津南开·八年级统考期末)为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5 mg/L,则第3次检测得到的氨氮含量是________ mg/L.
14.(2022春·天津河北·八年级统考期末)甲、乙两人在相同条件下进行射击练习,每人10次射击成绩的平均值都是8环,方差分别为,,则两人成绩比较稳定的是__________(填“甲”或“乙”).
三、解答题
15.(2022春·天津南开·八年级统考期末)某高校学生会向全校2900名学生发起了“爱心一日捐”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为___,图①中m的值是___;
(2)求本次你调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
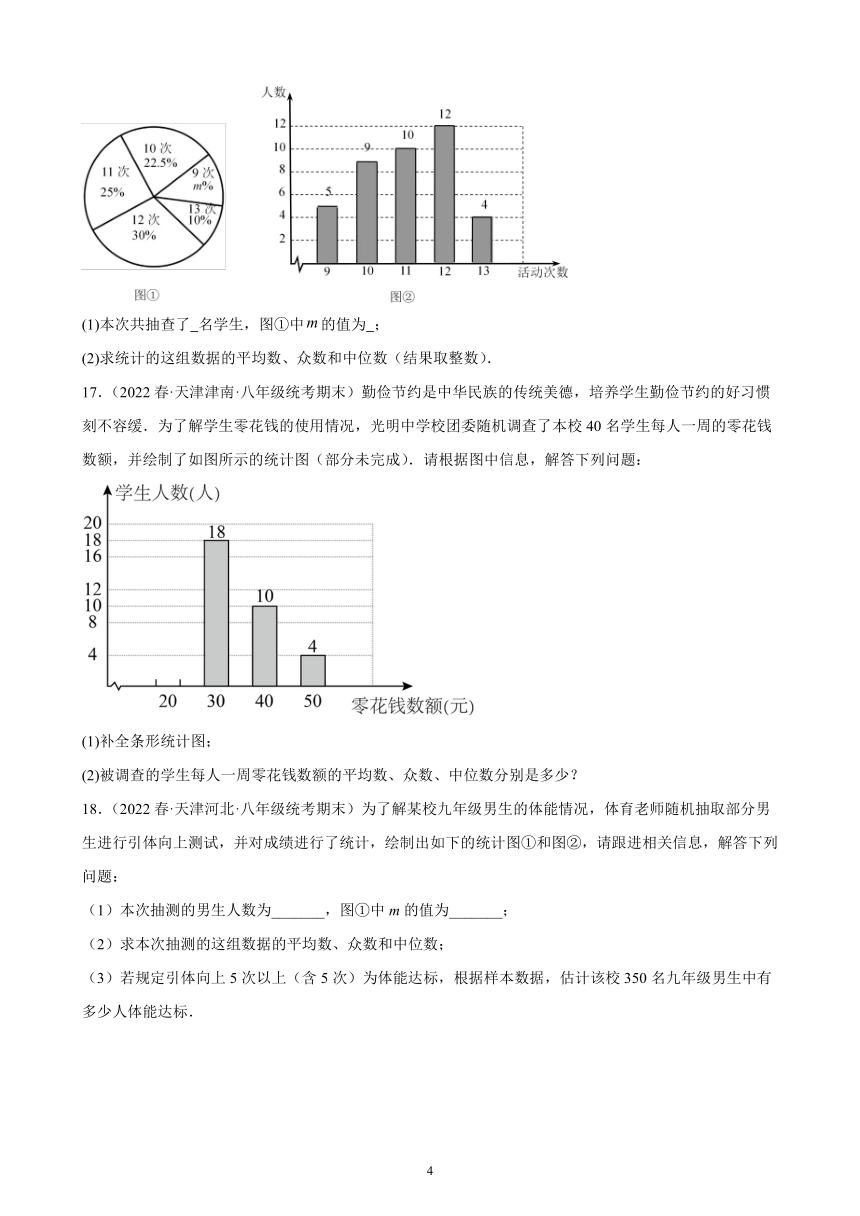
16.(2022春·天津滨海新·八年级统考期末)某学校鼓励学生参与社区志愿者活动,为了解学生志愿者活动的情况,随机调查了该校部分学生一年参加志愿者服务的次数.根据调查结果,绘制出如图的统计图①和图②.请根据相关信息,解答下列问题:
(1)本次共抽查了 名学生,图①中的值为 ;
(2)求统计的这组数据的平均数、众数和中位数(结果取整数).
17.(2022春·天津津南·八年级统考期末)勤俭节约是中华民族的传统美德,培养学生勤俭节约的好习惯刻不容缓.为了解学生零花钱的使用情况,光明中学校团委随机调查了本校40名学生每人一周的零花钱数额,并绘制了如图所示的统计图(部分未完成).请根据图中信息,解答下列问题:
(1)补全条形统计图;
(2)被调查的学生每人一周零花钱数额的平均数、众数、中位数分别是多少?
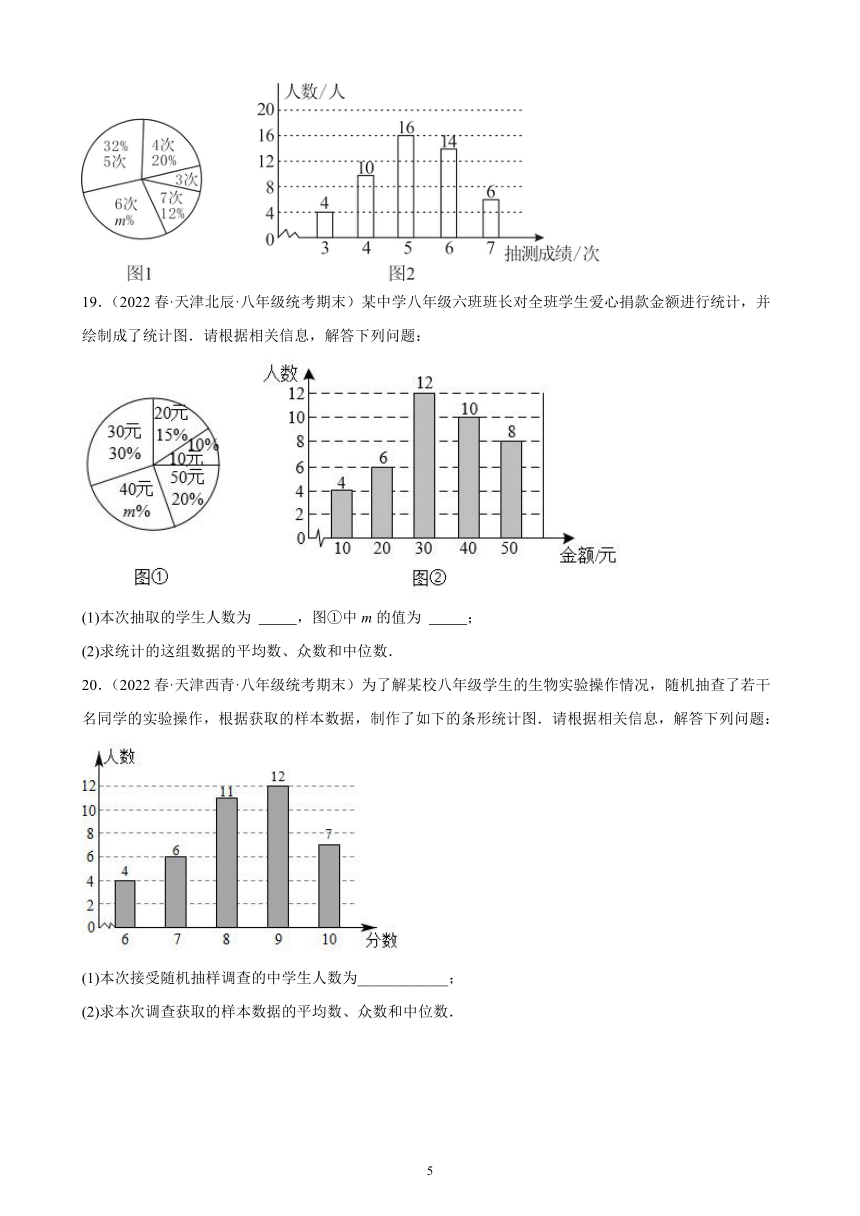
18.(2022春·天津河北·八年级统考期末)为了解某校九年级男生的体能情况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制出如下的统计图①和图②,请跟进相关信息,解答下列问题:
(1)本次抽测的男生人数为_______,图①中m的值为_______;
(2)求本次抽测的这组数据的平均数、众数和中位数;
(3)若规定引体向上5次以上(含5次)为体能达标,根据样本数据,估计该校350名九年级男生中有多少人体能达标.
19.(2022春·天津北辰·八年级统考期末)某中学八年级六班班长对全班学生爱心捐款金额进行统计,并绘制成了统计图.请根据相关信息,解答下列问题:
(1)本次抽取的学生人数为 ,图①中m的值为 ;
(2)求统计的这组数据的平均数、众数和中位数.
20.(2022春·天津西青·八年级统考期末)为了解某校八年级学生的生物实验操作情况,随机抽查了若干名同学的实验操作,根据获取的样本数据,制作了如下的条形统计图.请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的中学生人数为____________;
(2)求本次调查获取的样本数据的平均数、众数和中位数.
参考答案:
1.A
【分析】根据平均数的计算公式(为正整数)即可得.
【详解】解:这组数据的平均数为,
故选:A.
【点睛】本题考查了求平均数,熟记公式是解题关键.
2.C
【分析】根据求平均数的公式列出算式,即可求出的值.
【详解】解:,,4,,5,8这六个数的平均数是3,
,
解得:;
故选:.
【点睛】本题考查了平均数的求法,属于基础题,熟记求算术平均数的公式是解决本题的关键.
3.D
【分析】根据平均数求得的值,进而将这组数据从小到大重新排列,再根据中位数的定义求解即可.
【详解】解:∵一组数据,,3,,,的平均数是,
∴,
解得,
,
将这组数据从小到大重新排列为,
故中位数为,
故选D
【点睛】本题考查了已知平均数求未知数的值,求中位数,掌握求平均数与中位数是解题的关键.
4.B
【分析】根据众数和中位数的定义即可得.
【详解】解:因为在所得分数中,90出现的次数最多,为4次,
所以众数是90,
将所得分数按从小到大进行排序后,第5个数和第6个数的平均数即为中位数,
则中位数是,
故选:B.
【点睛】本题考查了众数和中位数,熟记定义是解题关键.
5.C
【分析】根据平均数、中位数、众数、方差的意义分析判断即可,得出鞋店老板最关心的数据.
【详解】解:∵众数体现数据的最集中的一点,这样可以确定进货的数量,
∴商家更应该关注鞋子尺码的众数.
故选:C.
【点睛】此题主要考查了统计的有关知识,主要是众数的意义.反映数据的统计量有平均数、中位数、众数、方差等,各有局限性,因此要对统计量进行合理的选择和恰当的运用.
6.C
【分析】根据中位数的定义即可求解.
【详解】统计每位选手得分时,会去掉一个最高分和一个最低分,这样做不会对数据的中间的数产生影响,即中位数.
故选:C.
【点睛】此题主要考查中位数的性质,解题的关键是熟知中位数的定义.
7.A
【分析】找出成绩的方差较小,且平均数较大的队员即可.
【详解】解:因为方差越小,表明发挥越稳定,且,
所以应该选择队员1或队员2,
又因为队员1的成绩的平均数为51大于队员2的成绩的平均数,
所以应该选择队员1,
故选:A.
【点睛】本题考查了利用平均数和方差进行决策,熟练掌握平均数好方差的意义是解题关键.
8.D
【分析】要判断哪-名学生的成绩比较稳定,而判断稳定性的量是由方差的大小来确定的,据此即可得解.
【详解】解:由于方差能反映数据的稳定性,所以要比较这两位同学数学测验成绩的稳定性用方差.
故选:D.
【点睛】此题考查方差的意义:方差是反映一组数据波动大小的特征数,方差越大,数据的波动性越大,方差越小,稳定性越好.
9.A
【分析】根据方差越小,说明数据的波动越小,越稳定即可得出结果.
【详解】解:方差就是和中心偏离的程度,用来衡量一批数据的波动大小(即这批数据偏离平均数的大小).在样本容量相同的情况下,方差越小,说明数据的波动越小,越稳定.
∵11<12.5,
∴(2)班比(1)班的成绩稳定.
故选:A.
【点睛】本题主要考查用方差判定数据的稳定程度,方差越小,说明数据的波动越小,越稳定.
10.85
【分析】利用加权平均数的计算公式即可得.
【详解】解:由题意,他本学期数学学期综合成绩是(分),
故答案为:85.
【点睛】本题考查了加权平均数,熟记加权平均数的公式是解题关键.
11.
【分析】根据中位数的定义进行计算即可.
【详解】解:将这17名队员的年龄从小到大排列,处在中间位置的一个数是14岁,
故答案为:14.
【点睛】本题考查中位数,理解中位数的定义是正确解答的前提.
12.甲
【分析】根据题意先算出甲、乙两位候选人的加权平均数,再进行比较,即可得出答案.
【详解】解:甲的平均成绩为:
(92×6+84×4)÷10=88.8(分),
乙的平均成绩为:
(90×6+86×4)÷10=88.4(分),
因为88.8>88.4,
所以甲将被录取.
故答案为:甲
【点睛】本题考查了加权平均数,熟练握加权平均数的计算公式是解题的关键.
13.1.
【详解】解:设第3次检测得到的氨氮含量是xmg//L,
由题意得 1.6+2+x+1.5+1.4+1.5=1.5×6,解得x=1.
故答案为1.
14.乙
【分析】根据方差的意义求解即可.
【详解】解:∵
∴
∴乙成绩比甲稳定.
故答案为:乙.
【点睛】本题主要考查方差的意义,掌握方差是反映一组数据的波动大小的一个量;方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
15.(1)50,32;(2)平均数为16,众数是10,中位数是15;(3)928人
【分析】(1)根据捐款数是5元的,所占的百分比是8%,即可求得总人数,然后根据百分比的意义求得m的值;
(2)根据平均数、众数、中位数的定义即可求解;
(3)利用总人数2900乘以对应的百分比即可求解.
【详解】解:(1)调查的学生数是:4÷8%=50(人),
m=×100=32.
故答案是:50,32;
(2)平均数是: =16(元),
众数是:10元,中位数是:15元;
(3)该校本次活动捐款金额为10元的学生人数是:2900×32%=928(人).
【点睛】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
16.(1)40;12.5;
(2)平均数为11,众数为12,中位数为11
【分析】(1)将条形图中各组数据相加可得,再计算m的值;
(2)根据平均数、众数、中位数定义可得.
(1)
本次抽查的学生共有5+9+10+12+4=40(名);
m%=×100%=12.5%,
即m=12.5,
故答案为:40;12.5;
(2)
平均数: =,
∵ 在这组样本数据中,12出现了12次,出现的次数最多,
∴ 这组样本数据的众数为12,
∵ 将这组样本数据按从小到大的顺序排列,
其中处于中间的两个数都是11,有,
∴ 这组样本数据的中位数为11.
【点睛】本题主要考查条形统计图与扇形统计图及平均数、众数、中位数,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据,根据图中数据进行计算.特别注意加权平均数的计算方法.
17.(1)见解析
(2)平均数为32.5、众数为30、中位数为30
【分析】(1)用调查学生人数40名,减去后面三组已知一周零花钱数30元,40元,50元的人数即可求解;
(2)根据平均数,中位数,众数的定义即可求解;
(1)
解:40-18-10-4=8(人)
条形图如图所示:
(2)
==32.5.
∴这组样本数据的平均数为32.5.
∵在这组样本数据中,30出现了18次,出现的次数最多,
∴这组样本数据的众数为30.
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是30,
有,
∴这组样本数据的中位数为30.
所以这组样本数据的平均数为32.5、众数为30、中位数为30.
【点睛】本题考查了条形统计图,以及平均数、众数、中位数的有关知识,解题的关键是看清题意,从条形统计图中获取信息.
18.(1)50、28;(2)平均数为5.16次,众数为5次,中位数为5次;(3)估计该校350名九年级男生中有252人体能达标.
【分析】(1)根据4次的人数及其百分比可得总人数,用6次的人数除以总人数求得m即可;
(2)根据平均数、众数、中位数的定义求解可得;
(3)总人数乘以样本中5、6、7次人数之和占被调查人数的比例可得.
【详解】(1)本次抽测的男生人数为10÷20%=50,
m%=×100%=28%,
所以m=28.
故答案为50、28.
(2)平均数为=5.16次,
众数为5次,
中位数为=5次;
(3)×350=252.
答:估计该校350名九年级男生中有252人体能达标.
【点睛】本题考查了条形统计图,读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.
19.(1)40人,25
(2)这组数据的平均数为33元,众数为30元,中位数为30元
【分析】(1)根据捐款金额为10元的学生的条形统计图和扇形统计图的信息即可得本次抽取的学生人数,再利用捐款金额为40元的学生人数除以本次抽取的学生人数即可得的值;
(2)根据平均数的计算公式、众数和中位数的定义即可得.
【详解】(1)解:本次抽取的学生人数为(人),
则,
所以,
故答案为:40,25.
(2)解:平均数为(元),
因为捐款30元的人数为12人,人数最多,
所以众数是30元,
将这组数据按从小到大进行排序后,第20个数和第21个数均是30元,
所以中位数是(元),
答:这组数据的平均数为33元,众数为30元,中位数为30元.
【点睛】本题考查了条形统计图和扇形统计图的信息关联、平均数、众数和中位数,熟练掌握统计调查的相关知识是解题关键.
20.(1)40人
(2)这40个样本数据平均数、众数、中位数分别是8.3分,9分,8分.
【分析】(1)把每小组的频数相加即可得到总人数;
(2)先求解40人所得的总分,再除以40可得平均数,再根据出现次数最多的数据可得众数,再判断排在最中间的两个数,求解这两个数的平均数即为中位数.
【详解】(1)解:本次接受随机抽样调查的中学生人数为:
(人).
故答案为:40人
(2)解:由平均数公式可得:(分),
出现次数最多的是9分,所以众数是9分,
排在最中间的两个数据是第20个,第21个数据,分别为8分,8分,
所以中位数是(8+8)÷2=8(分),
即这40个样本数据平均数、众数、中位数分别是8.3分,9分,8分;
【点睛】本题考查的是频数分布直方图,平均数,众数,中位数的含义,理解“先将得分从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数)是中位数”是解本题的关键.
一、单选题
1.(2022春·天津西青·八年级统考期末)一组数据:5,7,6,3,4的平均数是( )
A.5 B.6 C.4 D.8
2.(2022春·天津河北·八年级统考期末)-3,-2,4,x,5,8这六个数的平均数是3,则x的值为( )
A.4 B.5 C.6 D.7
3.(2022春·天津滨海新·八年级统考期末)已知一组数据,,3,,,的平均数是,那么这组数据的中位数是( )
A.1 B. C. D.
(2022春·天津西青·八年级统考期末)某校10名学生参加“交通安全”知识测试,他们得分情况如表中所示,则这10名学生所得分数的众数和中位数分别是( )
A.95和85 B.90和85 C.90和87.5 D.85和87.5
5.(2022春·天津津南·八年级统考期末)一家鞋店在一段时间内销售某种运动鞋30双,各种尺码鞋的销量如下表所示,对于进货,商家最关注的是由鞋码组成的这组数据的( )
尺码/cm 24 24.5 25 25.5 26 26.5 27
销售量/双 1 2 5 11 7 3 1
A.平均数 B.中位数 C.众数 D.方差
6.(2022春·天津东丽·八年级统考期末)歌唱比赛有二十位评委给选手打分,统计每位选手得分时,会去掉一个最高分和一个最低分,这样做,肯定不会对所有评委打分的哪一个统计量产生影响( )
A.平均分 B.众数 C.中位数 D.极差
7.(2022春·天津南开·八年级统考期末)2022年北京-张家口举办了冬季奥运会,很多学校也开设了相关的课程.下表记录了某校4名同学短道速滑选拔赛成绩的平均数与方差
队员1 队员2 队员3 队员4
平均数(秒) 51 50 51 50
方差(秒2) 3.5 3.5 14.5 14.5
据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A.队员1 B.队员2 C.队员3 D.队员4
8.(2022春·天津北辰·八年级统考期末)某跳远队准备选取一批队员参加比赛,要比较谁的成绩稳定,应选用的统计量是( )
A.平均数 B.众数 C.中位数 D.方差
9.(2022春·天津津南·八年级统考期末)八年级⑴班与⑵班各选出10名学生进行英文打字比赛,通过对参赛学生每分钟输入的单词个数进行统计,两班成绩的平均数相同,⑴班成绩的方差为12.5,⑵班成绩的方差为11,由此可知( )
A.⑵班比⑴班的成绩稳定 B.⑴班比⑵班的成绩稳定
C.两个班的成绩一样稳定 D.无法确定哪班的成绩更稳定
二、填空题
10.(2022春·天津西青·八年级统考期末)某校规定:学生的数学学科学期综合成绩是由平时、期中和期末三项成绩按的比例计算所得,若某同学本学期数学学科的平时、期中和期末成绩分别是90分,90分和80分,则他本学期数学学期综合成绩是_______分.
11.(2022春·天津北辰·八年级统考期末)如表是某体校女子体操队队员的年龄分布:
年龄/岁 13 14 15 16
人数 8 6 2 1
则该体校女子体操队队员年龄的中位数是 _____岁.
12.(2022春·天津津南·八年级统考期末)某公司招聘,甲、乙两位候选人面试和笔试成绩如表所示. 若面试与笔试成绩按6和4的权计算每人的平均成绩,从两人的成绩看,公司录取的是__________(填“甲” 或“乙”).
候选人 面试 笔试
甲 92 84
乙 90 86
13.(2022春·天津南开·八年级统考期末)为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5 mg/L,则第3次检测得到的氨氮含量是________ mg/L.
14.(2022春·天津河北·八年级统考期末)甲、乙两人在相同条件下进行射击练习,每人10次射击成绩的平均值都是8环,方差分别为,,则两人成绩比较稳定的是__________(填“甲”或“乙”).
三、解答题
15.(2022春·天津南开·八年级统考期末)某高校学生会向全校2900名学生发起了“爱心一日捐”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的学生人数为___,图①中m的值是___;
(2)求本次你调查获取的样本数据的平均数、众数和中位数;
(3)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
16.(2022春·天津滨海新·八年级统考期末)某学校鼓励学生参与社区志愿者活动,为了解学生志愿者活动的情况,随机调查了该校部分学生一年参加志愿者服务的次数.根据调查结果,绘制出如图的统计图①和图②.请根据相关信息,解答下列问题:
(1)本次共抽查了 名学生,图①中的值为 ;
(2)求统计的这组数据的平均数、众数和中位数(结果取整数).
17.(2022春·天津津南·八年级统考期末)勤俭节约是中华民族的传统美德,培养学生勤俭节约的好习惯刻不容缓.为了解学生零花钱的使用情况,光明中学校团委随机调查了本校40名学生每人一周的零花钱数额,并绘制了如图所示的统计图(部分未完成).请根据图中信息,解答下列问题:
(1)补全条形统计图;
(2)被调查的学生每人一周零花钱数额的平均数、众数、中位数分别是多少?
18.(2022春·天津河北·八年级统考期末)为了解某校九年级男生的体能情况,体育老师随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制出如下的统计图①和图②,请跟进相关信息,解答下列问题:
(1)本次抽测的男生人数为_______,图①中m的值为_______;
(2)求本次抽测的这组数据的平均数、众数和中位数;
(3)若规定引体向上5次以上(含5次)为体能达标,根据样本数据,估计该校350名九年级男生中有多少人体能达标.
19.(2022春·天津北辰·八年级统考期末)某中学八年级六班班长对全班学生爱心捐款金额进行统计,并绘制成了统计图.请根据相关信息,解答下列问题:
(1)本次抽取的学生人数为 ,图①中m的值为 ;
(2)求统计的这组数据的平均数、众数和中位数.
20.(2022春·天津西青·八年级统考期末)为了解某校八年级学生的生物实验操作情况,随机抽查了若干名同学的实验操作,根据获取的样本数据,制作了如下的条形统计图.请根据相关信息,解答下列问题:
(1)本次接受随机抽样调查的中学生人数为____________;
(2)求本次调查获取的样本数据的平均数、众数和中位数.
参考答案:
1.A
【分析】根据平均数的计算公式(为正整数)即可得.
【详解】解:这组数据的平均数为,
故选:A.
【点睛】本题考查了求平均数,熟记公式是解题关键.
2.C
【分析】根据求平均数的公式列出算式,即可求出的值.
【详解】解:,,4,,5,8这六个数的平均数是3,
,
解得:;
故选:.
【点睛】本题考查了平均数的求法,属于基础题,熟记求算术平均数的公式是解决本题的关键.
3.D
【分析】根据平均数求得的值,进而将这组数据从小到大重新排列,再根据中位数的定义求解即可.
【详解】解:∵一组数据,,3,,,的平均数是,
∴,
解得,
,
将这组数据从小到大重新排列为,
故中位数为,
故选D
【点睛】本题考查了已知平均数求未知数的值,求中位数,掌握求平均数与中位数是解题的关键.
4.B
【分析】根据众数和中位数的定义即可得.
【详解】解:因为在所得分数中,90出现的次数最多,为4次,
所以众数是90,
将所得分数按从小到大进行排序后,第5个数和第6个数的平均数即为中位数,
则中位数是,
故选:B.
【点睛】本题考查了众数和中位数,熟记定义是解题关键.
5.C
【分析】根据平均数、中位数、众数、方差的意义分析判断即可,得出鞋店老板最关心的数据.
【详解】解:∵众数体现数据的最集中的一点,这样可以确定进货的数量,
∴商家更应该关注鞋子尺码的众数.
故选:C.
【点睛】此题主要考查了统计的有关知识,主要是众数的意义.反映数据的统计量有平均数、中位数、众数、方差等,各有局限性,因此要对统计量进行合理的选择和恰当的运用.
6.C
【分析】根据中位数的定义即可求解.
【详解】统计每位选手得分时,会去掉一个最高分和一个最低分,这样做不会对数据的中间的数产生影响,即中位数.
故选:C.
【点睛】此题主要考查中位数的性质,解题的关键是熟知中位数的定义.
7.A
【分析】找出成绩的方差较小,且平均数较大的队员即可.
【详解】解:因为方差越小,表明发挥越稳定,且,
所以应该选择队员1或队员2,
又因为队员1的成绩的平均数为51大于队员2的成绩的平均数,
所以应该选择队员1,
故选:A.
【点睛】本题考查了利用平均数和方差进行决策,熟练掌握平均数好方差的意义是解题关键.
8.D
【分析】要判断哪-名学生的成绩比较稳定,而判断稳定性的量是由方差的大小来确定的,据此即可得解.
【详解】解:由于方差能反映数据的稳定性,所以要比较这两位同学数学测验成绩的稳定性用方差.
故选:D.
【点睛】此题考查方差的意义:方差是反映一组数据波动大小的特征数,方差越大,数据的波动性越大,方差越小,稳定性越好.
9.A
【分析】根据方差越小,说明数据的波动越小,越稳定即可得出结果.
【详解】解:方差就是和中心偏离的程度,用来衡量一批数据的波动大小(即这批数据偏离平均数的大小).在样本容量相同的情况下,方差越小,说明数据的波动越小,越稳定.
∵11<12.5,
∴(2)班比(1)班的成绩稳定.
故选:A.
【点睛】本题主要考查用方差判定数据的稳定程度,方差越小,说明数据的波动越小,越稳定.
10.85
【分析】利用加权平均数的计算公式即可得.
【详解】解:由题意,他本学期数学学期综合成绩是(分),
故答案为:85.
【点睛】本题考查了加权平均数,熟记加权平均数的公式是解题关键.
11.
【分析】根据中位数的定义进行计算即可.
【详解】解:将这17名队员的年龄从小到大排列,处在中间位置的一个数是14岁,
故答案为:14.
【点睛】本题考查中位数,理解中位数的定义是正确解答的前提.
12.甲
【分析】根据题意先算出甲、乙两位候选人的加权平均数,再进行比较,即可得出答案.
【详解】解:甲的平均成绩为:
(92×6+84×4)÷10=88.8(分),
乙的平均成绩为:
(90×6+86×4)÷10=88.4(分),
因为88.8>88.4,
所以甲将被录取.
故答案为:甲
【点睛】本题考查了加权平均数,熟练握加权平均数的计算公式是解题的关键.
13.1.
【详解】解:设第3次检测得到的氨氮含量是xmg//L,
由题意得 1.6+2+x+1.5+1.4+1.5=1.5×6,解得x=1.
故答案为1.
14.乙
【分析】根据方差的意义求解即可.
【详解】解:∵
∴
∴乙成绩比甲稳定.
故答案为:乙.
【点睛】本题主要考查方差的意义,掌握方差是反映一组数据的波动大小的一个量;方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
15.(1)50,32;(2)平均数为16,众数是10,中位数是15;(3)928人
【分析】(1)根据捐款数是5元的,所占的百分比是8%,即可求得总人数,然后根据百分比的意义求得m的值;
(2)根据平均数、众数、中位数的定义即可求解;
(3)利用总人数2900乘以对应的百分比即可求解.
【详解】解:(1)调查的学生数是:4÷8%=50(人),
m=×100=32.
故答案是:50,32;
(2)平均数是: =16(元),
众数是:10元,中位数是:15元;
(3)该校本次活动捐款金额为10元的学生人数是:2900×32%=928(人).
【点睛】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
16.(1)40;12.5;
(2)平均数为11,众数为12,中位数为11
【分析】(1)将条形图中各组数据相加可得,再计算m的值;
(2)根据平均数、众数、中位数定义可得.
(1)
本次抽查的学生共有5+9+10+12+4=40(名);
m%=×100%=12.5%,
即m=12.5,
故答案为:40;12.5;
(2)
平均数: =,
∵ 在这组样本数据中,12出现了12次,出现的次数最多,
∴ 这组样本数据的众数为12,
∵ 将这组样本数据按从小到大的顺序排列,
其中处于中间的两个数都是11,有,
∴ 这组样本数据的中位数为11.
【点睛】本题主要考查条形统计图与扇形统计图及平均数、众数、中位数,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据,根据图中数据进行计算.特别注意加权平均数的计算方法.
17.(1)见解析
(2)平均数为32.5、众数为30、中位数为30
【分析】(1)用调查学生人数40名,减去后面三组已知一周零花钱数30元,40元,50元的人数即可求解;
(2)根据平均数,中位数,众数的定义即可求解;
(1)
解:40-18-10-4=8(人)
条形图如图所示:
(2)
==32.5.
∴这组样本数据的平均数为32.5.
∵在这组样本数据中,30出现了18次,出现的次数最多,
∴这组样本数据的众数为30.
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是30,
有,
∴这组样本数据的中位数为30.
所以这组样本数据的平均数为32.5、众数为30、中位数为30.
【点睛】本题考查了条形统计图,以及平均数、众数、中位数的有关知识,解题的关键是看清题意,从条形统计图中获取信息.
18.(1)50、28;(2)平均数为5.16次,众数为5次,中位数为5次;(3)估计该校350名九年级男生中有252人体能达标.
【分析】(1)根据4次的人数及其百分比可得总人数,用6次的人数除以总人数求得m即可;
(2)根据平均数、众数、中位数的定义求解可得;
(3)总人数乘以样本中5、6、7次人数之和占被调查人数的比例可得.
【详解】(1)本次抽测的男生人数为10÷20%=50,
m%=×100%=28%,
所以m=28.
故答案为50、28.
(2)平均数为=5.16次,
众数为5次,
中位数为=5次;
(3)×350=252.
答:估计该校350名九年级男生中有252人体能达标.
【点睛】本题考查了条形统计图,读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.
19.(1)40人,25
(2)这组数据的平均数为33元,众数为30元,中位数为30元
【分析】(1)根据捐款金额为10元的学生的条形统计图和扇形统计图的信息即可得本次抽取的学生人数,再利用捐款金额为40元的学生人数除以本次抽取的学生人数即可得的值;
(2)根据平均数的计算公式、众数和中位数的定义即可得.
【详解】(1)解:本次抽取的学生人数为(人),
则,
所以,
故答案为:40,25.
(2)解:平均数为(元),
因为捐款30元的人数为12人,人数最多,
所以众数是30元,
将这组数据按从小到大进行排序后,第20个数和第21个数均是30元,
所以中位数是(元),
答:这组数据的平均数为33元,众数为30元,中位数为30元.
【点睛】本题考查了条形统计图和扇形统计图的信息关联、平均数、众数和中位数,熟练掌握统计调查的相关知识是解题关键.
20.(1)40人
(2)这40个样本数据平均数、众数、中位数分别是8.3分,9分,8分.
【分析】(1)把每小组的频数相加即可得到总人数;
(2)先求解40人所得的总分,再除以40可得平均数,再根据出现次数最多的数据可得众数,再判断排在最中间的两个数,求解这两个数的平均数即为中位数.
【详解】(1)解:本次接受随机抽样调查的中学生人数为:
(人).
故答案为:40人
(2)解:由平均数公式可得:(分),
出现次数最多的是9分,所以众数是9分,
排在最中间的两个数据是第20个,第21个数据,分别为8分,8分,
所以中位数是(8+8)÷2=8(分),
即这40个样本数据平均数、众数、中位数分别是8.3分,9分,8分;
【点睛】本题考查的是频数分布直方图,平均数,众数,中位数的含义,理解“先将得分从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数)是中位数”是解本题的关键.
