19.4解直角三角形[下学期]
图片预览







文档简介
课件23张PPT。 第19章 解直角三角形
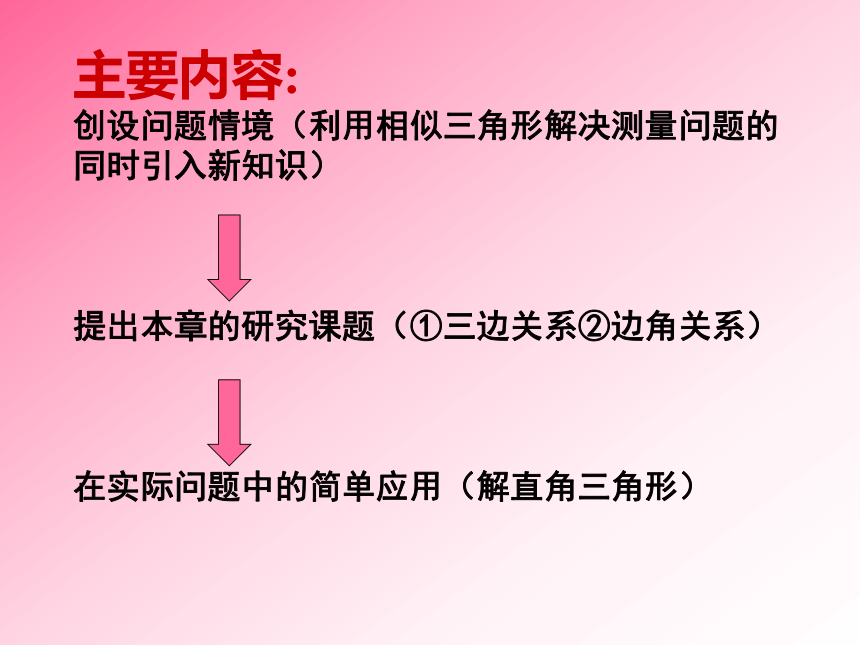
安吉实验初中 王星鑫 2005.1.28主要内容: 创设问题情境(利用相似三角形解决测量问题的同时引入新知识) ? ? 提出本章的研究课题(①三边关系②边角关系) ? ? 在实际问题中的简单应用(解直角三角形) ? 教学目标: 1. 经历勾股定理的探索过程. 2. 了解勾股定理的历史. 3. 知道30°、45°、60°角的三角函数值;会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它对应的锐角. 4. 理解并掌握直角三角形边角之间的关系. 5.能综合应用直角三角形的边角关系解决简单的实际问题 编排特点: (在传统教材中勾股定理与三角函数是分两章的,我们觉得两者合在一起是比较合理的.) 1.在呈现方式上,突出研究性,类似数学家的工作,是一个经历再创造的过程. 例如,对勾股定理和三角函数意义都是通过问题引出的。 2.勾股定理和三角函数的应用尽量都和实际问题联系起来,减少单纯解直角三角形的问题。 3.对实际问题的选取注意联系学生的生活实际。 4.本章安排了3个阅读材料,意在扩大学生的知识面,渗透人文精神。 5. 注意训练系统的科学性,减少操作性习题,增加探索性问题的比重。 6. 有关三角函数和解直角三角形的计算要充分利用计算器. 课时安排: 本章的教学时间大约需要13课时,建议分配如下: §19.1 测量-----------------1课时 §19.2 勾股定理-------------2课时 §19.3 锐角三角函数---------2课时 §19.4 解直角三角形---------4课时
复习------------------------2课时 课题学习--------------------2课时具体课时情况: ?§19.1 测量 本节起着承上启下的作用。通过一个实际问题——测量旗杆的高度,一方面帮助学生复习相似三角形有关知识,另一方面引出勾股定理及锐角三角函数。教学时,应启发学生探索用不同的方法解决问题的方案,同时应通过引导学生寻找更简单的方法解决该问题,形成优化意识.注意与课题学习相联系. §19.2 勾股定理 第一课时: 1.在方格子中根据面积探究: 等腰直角三角形(教材画出的)? 边长为3,4,5的直角三角形(要学生自己画的)
边长为5,12,13的直角三角形 (要学生自己画的)
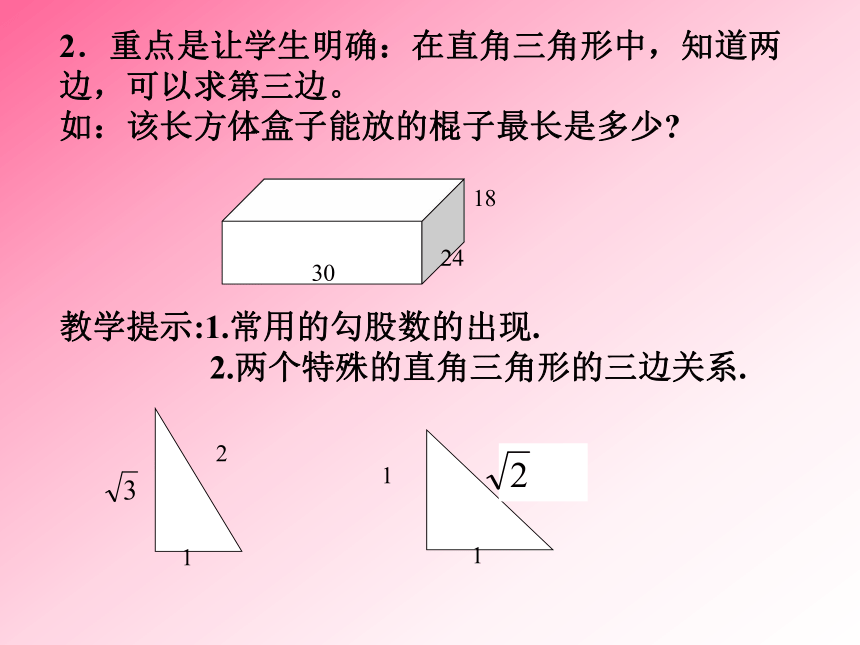
? 从而归纳得到勾股定理2.重点是让学生明确:在直角三角形中,知道两边,可以求第三边。 如:该长方体盒子能放的棍子最长是多少? ? ? 教学提示:1.常用的勾股数的出现. 2.两个特殊的直角三角形的三边关系. 第二课时: 1. 利用数形结合的思想:探索时应调动学生的积极性,让学生充分参与,证明时主要是讲清思路,而不只是介绍某一种证明方法。 2. 应用勾股定理解决实际问题,常见的两类:探索性问题和应用性问题。 ? 练习P104 P119 §19.3 锐角三角函数 第一课时:锐角三角函数 1. 锐角三角函数是根据19.1节中的问题的解法引入三角函数的意义,再得出0<sinA<1,0<cosA<1;tanA·cotA=1这些关系式的合理性。这两方面既是重点,也是难点。(要引导学生体会函数关系;适当的话可补充tanA与 cotA的取值范围,平方关系。) 2. 已知直角三角形的两边,会求某一锐角的四个三角函数值。 3.“在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。”这一结论是通过先让学生自己度量三角板,再利用30°正弦的意义发现的。还可以引导学生通过将两块完全相同的含30°的三角尺拼成一个等边三角形来说明这一结论。关于逆定理 第二课时: 1.掌握 30°、45°、60°三个特殊角的三角函数值。 2.用计算器求锐角三角函数值以及已知三角函数值求它对应的锐角。 在完成第109页“做一做”时,教师应强调:在含30°的三角板中,只须度量30°所对的直角边的长,再利用上面的结论求出斜边,最后利用勾股定理求出另一条直角边;在含45°的三角板中,只须度量直角边的长(腰长),再根据勾股定理求出斜边。然后利用三角函数的意义就可以求出30°、45°、60°三个特殊角的三角函数值。应引导学生从表中得出互余的两个角的三角函数之间的关系,适当的话可以进一步引导学生去发现函数与自变量之间的关系。用计算器求锐角三角函数值是以“CASIO fx—TL”型计算器为例介绍的。若学生的计算器型号不统一,教师应指导学生根据自己计算器的说明书掌握P110至P111例2~例5的解法。§19.4 解直角三角形 1. 在解决实际问题时,应使学生养成“先画图,再求解”的习惯。 2. 教学中不要简单地将解直角三角形的应用分为几种问题类型,而应注意问题选取的多样性。有时解决一个问题,往往可以用不同的三角函数关系式,这时应引导学生合理地选择关系式。 第一课时:P112---P113 综合运用勾股定理、三角函数解决简单的实际问题。两个例题,对第二题可分组探索以下问题: (1)是否可用勾股定理求BC? (2)是否可用余切函数求BC? (3)是否可用正弦函数求AC? (4)选用哪一种关系式较为简便? ?
并总结出:解直角三角形,只有下面两种情况: (1)已知两条边; (2)已知一条边和一个锐角 第二课时:P114,也可作为课题学习的一部分。 解决与仰角、俯角有关的实际问题,了解“铅垂线、水平线、仰角、俯角”等概念。 自制测角仪,计算结果要符合实际。第三课时: 解决与坡度相关的实际问题,了解“铅垂高度、水平长度、坡角、坡度”等概念。 第四课时: 综合运用本章所学的知识解决实际问题,学会把实际问题转化为数学问题,再把平面图形分割为若干个直角三角形、矩形、或直角梯形,培养建模能力。 45?,15?,120?.30?,45?,105?;45?,60?,75?;30?,15?,135 ? ;课题学习:
该课题是对第18章和19章的小结。通过这两章的学习,对一个测量问题,学生一般可以有几种不同的方法来解决,但在实际问题中,由于条件的限制,常常需要寻找一个切实可行的方法。正是基于这一点,安排了这一个课题学习。在研究的过程中,教师应让学生充分发表意见,让学生自己去体会各种方法的优劣,而不能简单地把自己的评判标准强加给学生。 实际操作时尽量用特殊角 。1. 可以用什么测量方法?每一种方法的依据是什么? 2. 每一种方法要用哪些工具? 3. 应测量得到哪些有关的数据? 4. 如何计算最后的结果? 整一章结束后,可以对直角三角形的性质从边、角、边角三方面进行总结:参考书本。
安吉实验初中 王星鑫 2005.1.28主要内容: 创设问题情境(利用相似三角形解决测量问题的同时引入新知识) ? ? 提出本章的研究课题(①三边关系②边角关系) ? ? 在实际问题中的简单应用(解直角三角形) ? 教学目标: 1. 经历勾股定理的探索过程. 2. 了解勾股定理的历史. 3. 知道30°、45°、60°角的三角函数值;会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它对应的锐角. 4. 理解并掌握直角三角形边角之间的关系. 5.能综合应用直角三角形的边角关系解决简单的实际问题 编排特点: (在传统教材中勾股定理与三角函数是分两章的,我们觉得两者合在一起是比较合理的.) 1.在呈现方式上,突出研究性,类似数学家的工作,是一个经历再创造的过程. 例如,对勾股定理和三角函数意义都是通过问题引出的。 2.勾股定理和三角函数的应用尽量都和实际问题联系起来,减少单纯解直角三角形的问题。 3.对实际问题的选取注意联系学生的生活实际。 4.本章安排了3个阅读材料,意在扩大学生的知识面,渗透人文精神。 5. 注意训练系统的科学性,减少操作性习题,增加探索性问题的比重。 6. 有关三角函数和解直角三角形的计算要充分利用计算器. 课时安排: 本章的教学时间大约需要13课时,建议分配如下: §19.1 测量-----------------1课时 §19.2 勾股定理-------------2课时 §19.3 锐角三角函数---------2课时 §19.4 解直角三角形---------4课时
复习------------------------2课时 课题学习--------------------2课时具体课时情况: ?§19.1 测量 本节起着承上启下的作用。通过一个实际问题——测量旗杆的高度,一方面帮助学生复习相似三角形有关知识,另一方面引出勾股定理及锐角三角函数。教学时,应启发学生探索用不同的方法解决问题的方案,同时应通过引导学生寻找更简单的方法解决该问题,形成优化意识.注意与课题学习相联系. §19.2 勾股定理 第一课时: 1.在方格子中根据面积探究: 等腰直角三角形(教材画出的)? 边长为3,4,5的直角三角形(要学生自己画的)
边长为5,12,13的直角三角形 (要学生自己画的)
? 从而归纳得到勾股定理2.重点是让学生明确:在直角三角形中,知道两边,可以求第三边。 如:该长方体盒子能放的棍子最长是多少? ? ? 教学提示:1.常用的勾股数的出现. 2.两个特殊的直角三角形的三边关系. 第二课时: 1. 利用数形结合的思想:探索时应调动学生的积极性,让学生充分参与,证明时主要是讲清思路,而不只是介绍某一种证明方法。 2. 应用勾股定理解决实际问题,常见的两类:探索性问题和应用性问题。 ? 练习P104 P119 §19.3 锐角三角函数 第一课时:锐角三角函数 1. 锐角三角函数是根据19.1节中的问题的解法引入三角函数的意义,再得出0<sinA<1,0<cosA<1;tanA·cotA=1这些关系式的合理性。这两方面既是重点,也是难点。(要引导学生体会函数关系;适当的话可补充tanA与 cotA的取值范围,平方关系。) 2. 已知直角三角形的两边,会求某一锐角的四个三角函数值。 3.“在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。”这一结论是通过先让学生自己度量三角板,再利用30°正弦的意义发现的。还可以引导学生通过将两块完全相同的含30°的三角尺拼成一个等边三角形来说明这一结论。关于逆定理 第二课时: 1.掌握 30°、45°、60°三个特殊角的三角函数值。 2.用计算器求锐角三角函数值以及已知三角函数值求它对应的锐角。 在完成第109页“做一做”时,教师应强调:在含30°的三角板中,只须度量30°所对的直角边的长,再利用上面的结论求出斜边,最后利用勾股定理求出另一条直角边;在含45°的三角板中,只须度量直角边的长(腰长),再根据勾股定理求出斜边。然后利用三角函数的意义就可以求出30°、45°、60°三个特殊角的三角函数值。应引导学生从表中得出互余的两个角的三角函数之间的关系,适当的话可以进一步引导学生去发现函数与自变量之间的关系。用计算器求锐角三角函数值是以“CASIO fx—TL”型计算器为例介绍的。若学生的计算器型号不统一,教师应指导学生根据自己计算器的说明书掌握P110至P111例2~例5的解法。§19.4 解直角三角形 1. 在解决实际问题时,应使学生养成“先画图,再求解”的习惯。 2. 教学中不要简单地将解直角三角形的应用分为几种问题类型,而应注意问题选取的多样性。有时解决一个问题,往往可以用不同的三角函数关系式,这时应引导学生合理地选择关系式。 第一课时:P112---P113 综合运用勾股定理、三角函数解决简单的实际问题。两个例题,对第二题可分组探索以下问题: (1)是否可用勾股定理求BC? (2)是否可用余切函数求BC? (3)是否可用正弦函数求AC? (4)选用哪一种关系式较为简便? ?
并总结出:解直角三角形,只有下面两种情况: (1)已知两条边; (2)已知一条边和一个锐角 第二课时:P114,也可作为课题学习的一部分。 解决与仰角、俯角有关的实际问题,了解“铅垂线、水平线、仰角、俯角”等概念。 自制测角仪,计算结果要符合实际。第三课时: 解决与坡度相关的实际问题,了解“铅垂高度、水平长度、坡角、坡度”等概念。 第四课时: 综合运用本章所学的知识解决实际问题,学会把实际问题转化为数学问题,再把平面图形分割为若干个直角三角形、矩形、或直角梯形,培养建模能力。 45?,15?,120?.30?,45?,105?;45?,60?,75?;30?,15?,135 ? ;课题学习:
该课题是对第18章和19章的小结。通过这两章的学习,对一个测量问题,学生一般可以有几种不同的方法来解决,但在实际问题中,由于条件的限制,常常需要寻找一个切实可行的方法。正是基于这一点,安排了这一个课题学习。在研究的过程中,教师应让学生充分发表意见,让学生自己去体会各种方法的优劣,而不能简单地把自己的评判标准强加给学生。 实际操作时尽量用特殊角 。1. 可以用什么测量方法?每一种方法的依据是什么? 2. 每一种方法要用哪些工具? 3. 应测量得到哪些有关的数据? 4. 如何计算最后的结果? 整一章结束后,可以对直角三角形的性质从边、角、边角三方面进行总结:参考书本。
