人教版六年级下册 圆柱的体积 教学设计
文档属性
| 名称 | 人教版六年级下册 圆柱的体积 教学设计 |
|
|
| 格式 | docx | ||
| 文件大小 | 435.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 00:00:00 | ||
图片预览

文档简介
圆柱的体积
一、教学目标定位
1.联系长方体的体积,重点理解圆柱体积的推导。
2.领域视角下,理解体积度量的本质。
二、环节目标与材料
环节与目标 学习材料
环节一:探究体积 1.运用知识的迁移,由长方体体积引入,理解体积度量就是在度量体积单位个数。 2.理解所有直柱体都可以用一层的体积单位个数乘层数来快速计数。 任务:请你用自己的办法数数这个圆柱中包含几个体积单位?(π取3) (数数、算算,请把你的方法清楚地表示出来)
环节二:知识联系,建立完整知识结构 贯通所有直柱体的体积度量,拓展到体积与面积度量的相同点。
三、教学过程展开举例
【环节一】探究体积
回顾五年级时,长方体的体积是怎么研究的。
主问题:为什么三个长度相乘就是体积了呢?
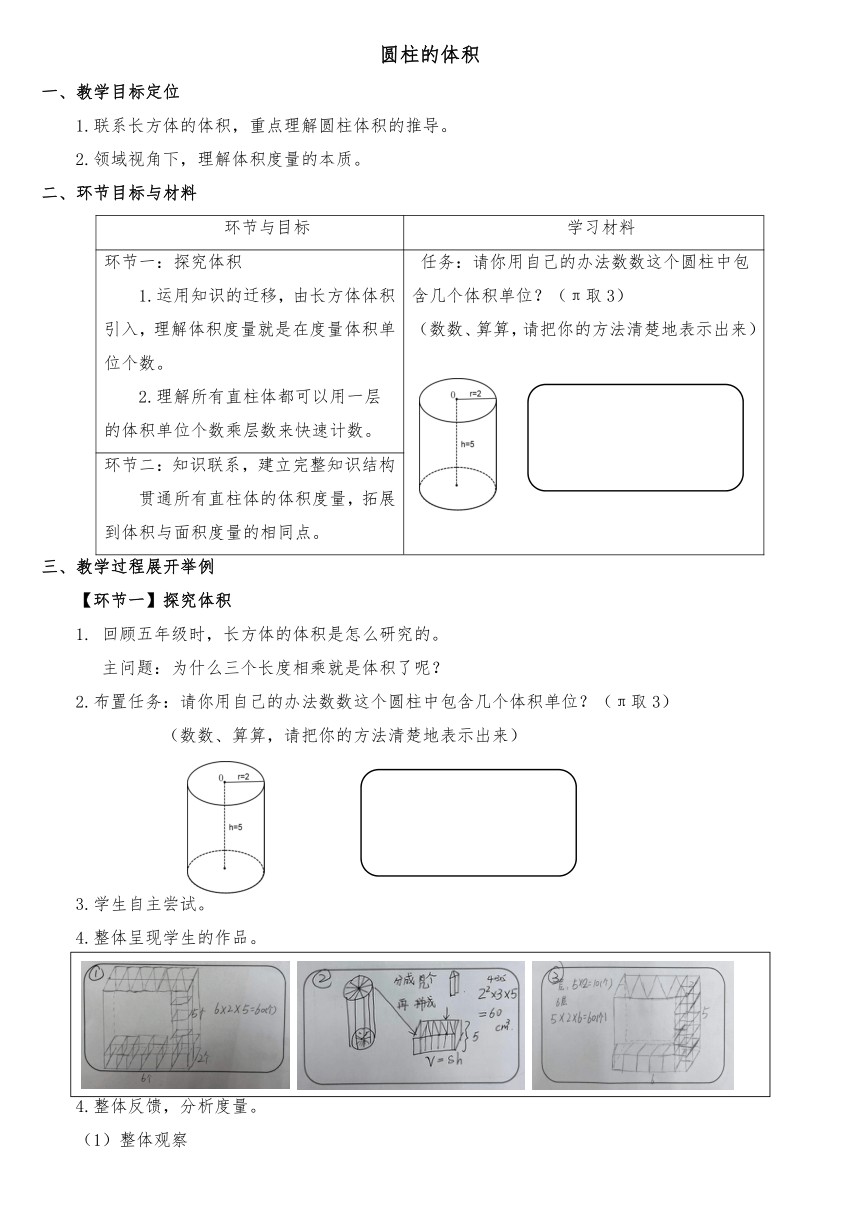
2.布置任务:请你用自己的办法数数这个圆柱中包含几个体积单位?(π取3)
(数数、算算,请把你的方法清楚地表示出来)
3.学生自主尝试。
4.整体呈现学生的作品。
4.整体反馈,分析度量。
(1)整体观察
①师主问:这些方法有什么相同点?
②师追问:为什么要转化成长方体?
小结:圆柱的底面是个圆,体积单位不好摆,转化成长方体就好摆了。
转化分析
师主问:先来看第一种方法,谁看懂他是怎么数的了?
生描述长方体与圆柱之间的转化关系。
师追问:那你是怎么数出体积单位的个数的呢?
生:这里的长是圆柱底面周长的一半,也就是一行能摆πr个,宽是半径,表示能摆这样的r行,高是h,表示能摆h层。
师追问:这里的6×2是什么呀?
生:是一层有12个
师追问:那5呢?谁能再来完整地说一说?
师主问:那第二种方法你看明白他是怎么数的了吗?
师追问:和方法一想的一样吗?
生:想的一样,只是他没有把体积单位画出来。
师主问:方法三中一层的体积单位的个数在哪里?层数呢?
思辨1:这两个同学数的方法不同,但什么是一样的?
生:都是用一层的体积单位的个数乘层数来算的。
小结:是的,刚才不论怎么数都是在数圆柱中的体积单位的个数(都是60个),原来你们都数出了 πr h 个。
师主问:那这个同学是怎么数的,你们看懂了吗?
呈现学生材料,并交流。
生:这里的πr 不是底面积,是一层有12个体积单位,一共有这样的5层。
师追问:你是怎么知道一层是πr 个的啊?
生:这里应该是πr ×1,要把高加上的。
师:原来你是受到了圆的面积的影响,在你的脑海里已经转化过了,这个底面上能放πr 个面积单位,高是1,那一层就能放πr 个体积单位。
思辨2:长方体的体积和圆柱的体积,我们研究时有什么相同之处?
生1:都是在数体积单位的个数。
生2:都是用一层的体积单位个数×层数来数的。
师主问:那还有哪些立体图形也可以用这个道理来数体积单位的个数呢?
学生探究讨论得出直柱体。
思辨3:那圆锥可以用这个道理来数体积单位的个数吗?为什么?
生:圆锥不行,它每一层体积单位的个数都不一样。
环节二:知识联系,建立完整知识结构
师主问:这些直柱体的体积单位个数都是怎么数的?
生:都可以转化成长方体,都用了一层的体积单位个数乘层数。
师追问:那它们底面的面积单位个数是怎么数的?
生:都可以转化成长方形,都用了一行的面积单位个数乘行数。
思辨:不管是研究体积还是面积,有什么相同的?
生:都可以转化,都用了几个几来算。
总结:是的,不论是研究体积还是面积,都可以转化成基本图形,也都能用几个几来快速计数它们单位的个数。
一、教学目标定位
1.联系长方体的体积,重点理解圆柱体积的推导。
2.领域视角下,理解体积度量的本质。
二、环节目标与材料
环节与目标 学习材料
环节一:探究体积 1.运用知识的迁移,由长方体体积引入,理解体积度量就是在度量体积单位个数。 2.理解所有直柱体都可以用一层的体积单位个数乘层数来快速计数。 任务:请你用自己的办法数数这个圆柱中包含几个体积单位?(π取3) (数数、算算,请把你的方法清楚地表示出来)
环节二:知识联系,建立完整知识结构 贯通所有直柱体的体积度量,拓展到体积与面积度量的相同点。
三、教学过程展开举例
【环节一】探究体积
回顾五年级时,长方体的体积是怎么研究的。
主问题:为什么三个长度相乘就是体积了呢?
2.布置任务:请你用自己的办法数数这个圆柱中包含几个体积单位?(π取3)
(数数、算算,请把你的方法清楚地表示出来)
3.学生自主尝试。
4.整体呈现学生的作品。
4.整体反馈,分析度量。
(1)整体观察
①师主问:这些方法有什么相同点?
②师追问:为什么要转化成长方体?
小结:圆柱的底面是个圆,体积单位不好摆,转化成长方体就好摆了。
转化分析
师主问:先来看第一种方法,谁看懂他是怎么数的了?
生描述长方体与圆柱之间的转化关系。
师追问:那你是怎么数出体积单位的个数的呢?
生:这里的长是圆柱底面周长的一半,也就是一行能摆πr个,宽是半径,表示能摆这样的r行,高是h,表示能摆h层。
师追问:这里的6×2是什么呀?
生:是一层有12个
师追问:那5呢?谁能再来完整地说一说?
师主问:那第二种方法你看明白他是怎么数的了吗?
师追问:和方法一想的一样吗?
生:想的一样,只是他没有把体积单位画出来。
师主问:方法三中一层的体积单位的个数在哪里?层数呢?
思辨1:这两个同学数的方法不同,但什么是一样的?
生:都是用一层的体积单位的个数乘层数来算的。
小结:是的,刚才不论怎么数都是在数圆柱中的体积单位的个数(都是60个),原来你们都数出了 πr h 个。
师主问:那这个同学是怎么数的,你们看懂了吗?
呈现学生材料,并交流。
生:这里的πr 不是底面积,是一层有12个体积单位,一共有这样的5层。
师追问:你是怎么知道一层是πr 个的啊?
生:这里应该是πr ×1,要把高加上的。
师:原来你是受到了圆的面积的影响,在你的脑海里已经转化过了,这个底面上能放πr 个面积单位,高是1,那一层就能放πr 个体积单位。
思辨2:长方体的体积和圆柱的体积,我们研究时有什么相同之处?
生1:都是在数体积单位的个数。
生2:都是用一层的体积单位个数×层数来数的。
师主问:那还有哪些立体图形也可以用这个道理来数体积单位的个数呢?
学生探究讨论得出直柱体。
思辨3:那圆锥可以用这个道理来数体积单位的个数吗?为什么?
生:圆锥不行,它每一层体积单位的个数都不一样。
环节二:知识联系,建立完整知识结构
师主问:这些直柱体的体积单位个数都是怎么数的?
生:都可以转化成长方体,都用了一层的体积单位个数乘层数。
师追问:那它们底面的面积单位个数是怎么数的?
生:都可以转化成长方形,都用了一行的面积单位个数乘行数。
思辨:不管是研究体积还是面积,有什么相同的?
生:都可以转化,都用了几个几来算。
总结:是的,不论是研究体积还是面积,都可以转化成基本图形,也都能用几个几来快速计数它们单位的个数。
