解直角三角形应用(第二课时)[下学期]
文档属性
| 名称 | 解直角三角形应用(第二课时)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 228.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-05-17 00:00:00 | ||
图片预览

文档简介
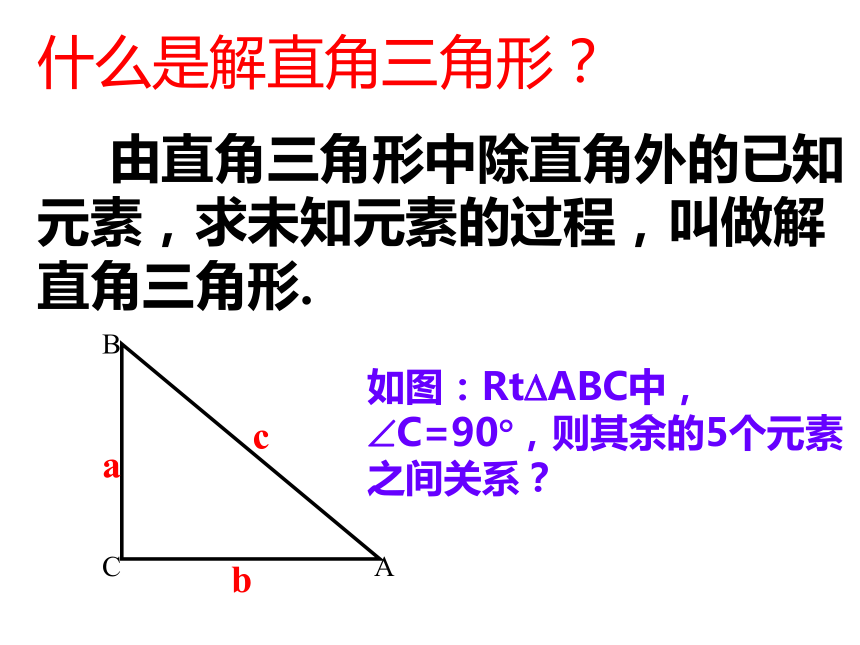
课件9张PPT。(二)什么是解直角三角形?
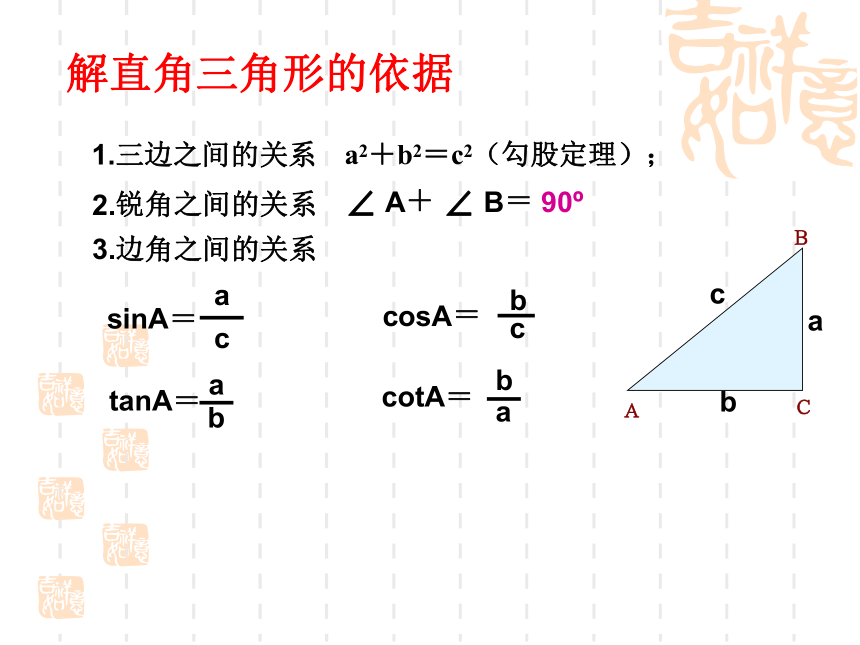
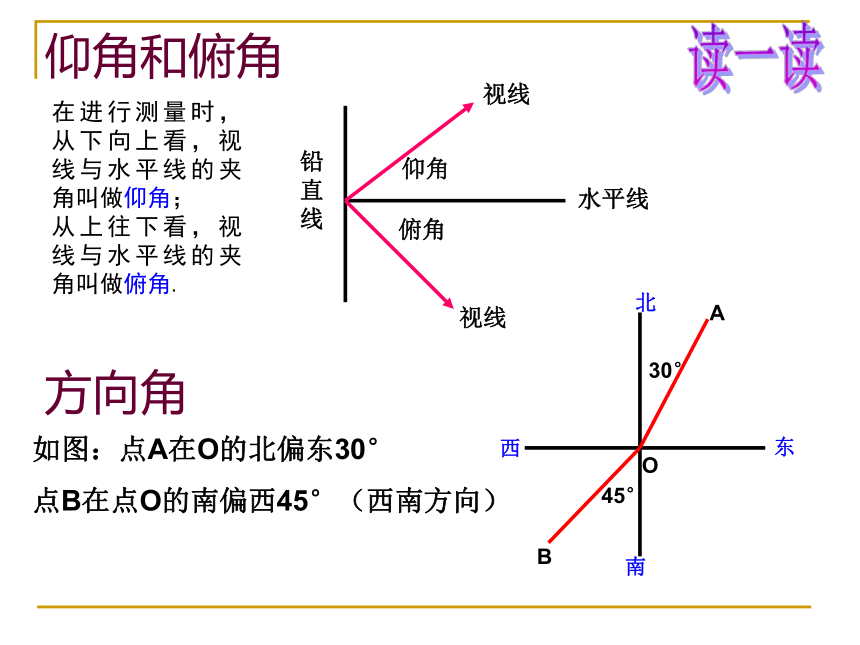
由直角三角形中除直角外的已知元素,求未知元素的过程,叫做解直角三角形.如图:Rt?ABC中,?C=90?,则其余的5个元素之间关系?bca1.三边之间的关系a2+b2=c2(勾股定理);2.锐角之间的关系∠ A+ ∠ B= 90o3.边角之间的关系sinA=解直角三角形的依据仰角和俯角铅直线水平线视线视线仰角俯角方向角如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)读一读在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
例 1解 在Rt△BDE中,
BE=DE×tan a
=AC×tan a
=22.7×tan 22°
≈9.17,
所以 AB=BE+AE
=BE+CD
=9.17+1.20
≈10.4(米).
答: 电线杆的高度约为10.4米.如图19.4.4,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)在山顶上处D有一铁塔,在塔顶B处测得地面上一点A的俯角α=60o,在塔底D测得点A的俯角β=45o,已知塔高BD=30米,求山高CD。ABCDαβ例 2解:在RtΔADC中,∠C =900
∵ ∠CAD =β=450 ∠CDA=450
∴ ∠CAD = ∠CDA
∴CD=AC
设CD为x米 则AC=x米
在RtΔABC中 ∠C =900
∵ ∠CAB=α=600
∴BC=AC·tan600 即x+30= x∴ x-x=30∴x= 15 +15 (米)答:山高CD为(15 +15) 米 某人在A处测得大厦的仰角∠BAC为300 ,沿AC方向行20米至D处,测得仰角∠BDC 为450,求此大厦的高度BC.ABDC300450例 31.如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看低平面控制点B的俯角α=16031/,求飞机A到控制点B的距离.(精确到1米)α练习ABC2. 两座建筑AB及CD,其地面距离AC为50.4米,从AB的顶点B测得CD的顶部D的仰角β=25゜,测得其底部C的俯角a=50゜,求两座建筑物AB及CD的高.(精确到0.1米)作业2. 同步导学第130页—第132页的
1、2、3、4、5、6、7、8、9、10题1.课本第116页习题19.4的第3题
由直角三角形中除直角外的已知元素,求未知元素的过程,叫做解直角三角形.如图:Rt?ABC中,?C=90?,则其余的5个元素之间关系?bca1.三边之间的关系a2+b2=c2(勾股定理);2.锐角之间的关系∠ A+ ∠ B= 90o3.边角之间的关系sinA=解直角三角形的依据仰角和俯角铅直线水平线视线视线仰角俯角方向角如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)读一读在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
例 1解 在Rt△BDE中,
BE=DE×tan a
=AC×tan a
=22.7×tan 22°
≈9.17,
所以 AB=BE+AE
=BE+CD
=9.17+1.20
≈10.4(米).
答: 电线杆的高度约为10.4米.如图19.4.4,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)在山顶上处D有一铁塔,在塔顶B处测得地面上一点A的俯角α=60o,在塔底D测得点A的俯角β=45o,已知塔高BD=30米,求山高CD。ABCDαβ例 2解:在RtΔADC中,∠C =900
∵ ∠CAD =β=450 ∠CDA=450
∴ ∠CAD = ∠CDA
∴CD=AC
设CD为x米 则AC=x米
在RtΔABC中 ∠C =900
∵ ∠CAB=α=600
∴BC=AC·tan600 即x+30= x∴ x-x=30∴x= 15 +15 (米)答:山高CD为(15 +15) 米 某人在A处测得大厦的仰角∠BAC为300 ,沿AC方向行20米至D处,测得仰角∠BDC 为450,求此大厦的高度BC.ABDC300450例 31.如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看低平面控制点B的俯角α=16031/,求飞机A到控制点B的距离.(精确到1米)α练习ABC2. 两座建筑AB及CD,其地面距离AC为50.4米,从AB的顶点B测得CD的顶部D的仰角β=25゜,测得其底部C的俯角a=50゜,求两座建筑物AB及CD的高.(精确到0.1米)作业2. 同步导学第130页—第132页的
1、2、3、4、5、6、7、8、9、10题1.课本第116页习题19.4的第3题
