解直角三角形(一)[下学期]
图片预览


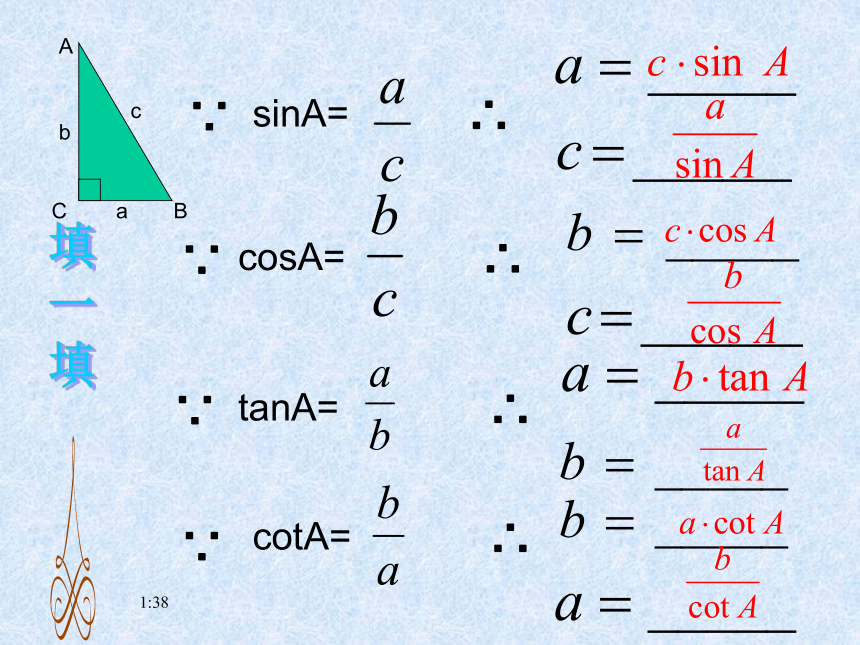


文档简介
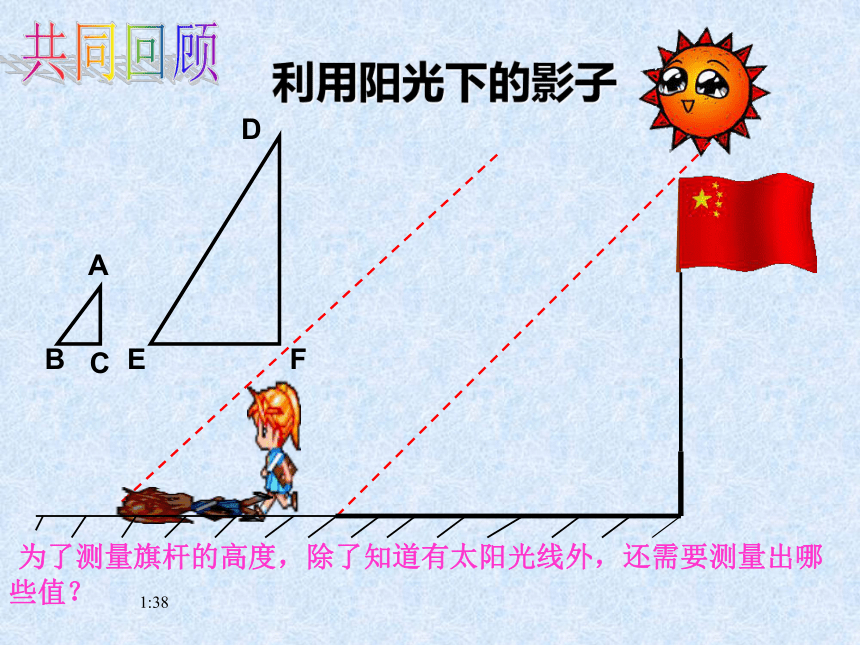
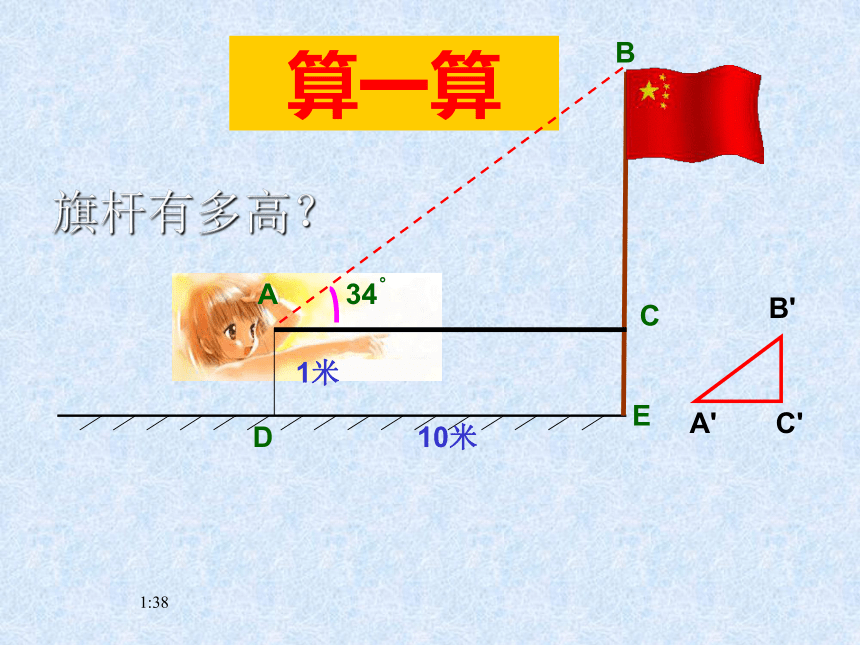
课件15张PPT。17:14稽东镇中学 尉嗣侃17:14 为了测量旗杆的高度,除了知道有太阳光线外,还需要测量出哪 些值?利用阳光下的影子 共同回顾17:14算一算34。ADECB10米1米旗杆有多高?17:14 a2+b2=c2
边与角关系
sinA= = cosA= =
tanA= = cotA= =
三边关系哈哈!,这就是直角三角形除直角以外的5元素之间的关系——可要记住了两锐角互余解题工具cosBsinBtanBcotB解直角三角形17:14sinA=cosA=tanA=cotA=∵∵∵∵∴∴∴∴填
一
填17:141.除直角外,在a,b,c∠A, ∠B五个元素中若已知一个元素,能求出其余四个元素吗?2.若已知两个元素,能求出其余三个元素吗?(分情况讨论)探索与思考17:14 在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.
1.已知两条边:
2已知一条边和一个锐角:在解直角三角形中,常会遇到近似计算,书上除特别说明外,边长保留四个有效数字,角度精确到1′⑴两直角边
⑵一直角边和斜边 ⑴一直角边和一锐角
⑵ 斜边和一锐角
解直角三角形只有下面两种情形:17:14如图所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?试一试17:14解 利用勾股定理可以求出折断倒下部分的长度为
在此例中,我们还可以利用直角三角形的边角之间的关系求出另外两个锐角 26+10=36(米).
所以,大树在折断之前高为36米.17:14 如图,东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米)17:14解 在Rt△ABC 中,因为
∠CAB=90゜-∠DAC=50゜
=tan∠CAB
所以 BC=AB?tan∠CAB
=2000×tan50゜≈2384(米).
又因为
所以 AC=
答:敌舰与A、B两炮台的距离分别约为3111米和2384米.17:14<1>是否可用余切函数求BC?是否可用正弦函数求AC?
想一想<2>在求出BC后是否
可用勾股定理求AC?
???17:14. 在Rt△ABC中, ∠C=90°,a=12, b=5,解这个直角三角形. 在电线杆离地面8米高的地方向地面 拉一条长10米的缆绳,问这条缆绳应固定在距离电线杆底部多远的地方?
动动脑筋17:14. 海船以32.6海里/时的速度向正北方向航行,在A处看灯塔Q在海船的北偏东30゜处,半小时后航行到B处,发现此时灯塔Q与海船的距离最短,求灯塔Q到B处的距离.(画出图形后计算,精确到0.1海里)
17:141.说一说本节课我有哪些收获?
2.本节课我还有哪些疑惑?课堂聚焦
边与角关系
sinA= = cosA= =
tanA= = cotA= =
三边关系哈哈!,这就是直角三角形除直角以外的5元素之间的关系——可要记住了两锐角互余解题工具cosBsinBtanBcotB解直角三角形17:14sinA=cosA=tanA=cotA=∵∵∵∵∴∴∴∴填
一
填17:141.除直角外,在a,b,c∠A, ∠B五个元素中若已知一个元素,能求出其余四个元素吗?2.若已知两个元素,能求出其余三个元素吗?(分情况讨论)探索与思考17:14 在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形.
1.已知两条边:
2已知一条边和一个锐角:在解直角三角形中,常会遇到近似计算,书上除特别说明外,边长保留四个有效数字,角度精确到1′⑴两直角边
⑵一直角边和斜边 ⑴一直角边和一锐角
⑵ 斜边和一锐角
解直角三角形只有下面两种情形:17:14如图所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?试一试17:14解 利用勾股定理可以求出折断倒下部分的长度为
在此例中,我们还可以利用直角三角形的边角之间的关系求出另外两个锐角 26+10=36(米).
所以,大树在折断之前高为36米.17:14 如图,东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米)17:14解 在Rt△ABC 中,因为
∠CAB=90゜-∠DAC=50゜
=tan∠CAB
所以 BC=AB?tan∠CAB
=2000×tan50゜≈2384(米).
又因为
所以 AC=
答:敌舰与A、B两炮台的距离分别约为3111米和2384米.17:14<1>是否可用余切函数求BC?是否可用正弦函数求AC?
想一想<2>在求出BC后是否
可用勾股定理求AC?
???17:14. 在Rt△ABC中, ∠C=90°,a=12, b=5,解这个直角三角形. 在电线杆离地面8米高的地方向地面 拉一条长10米的缆绳,问这条缆绳应固定在距离电线杆底部多远的地方?
动动脑筋17:14. 海船以32.6海里/时的速度向正北方向航行,在A处看灯塔Q在海船的北偏东30゜处,半小时后航行到B处,发现此时灯塔Q与海船的距离最短,求灯塔Q到B处的距离.(画出图形后计算,精确到0.1海里)
17:141.说一说本节课我有哪些收获?
2.本节课我还有哪些疑惑?课堂聚焦
