解直角三角形3[下学期]

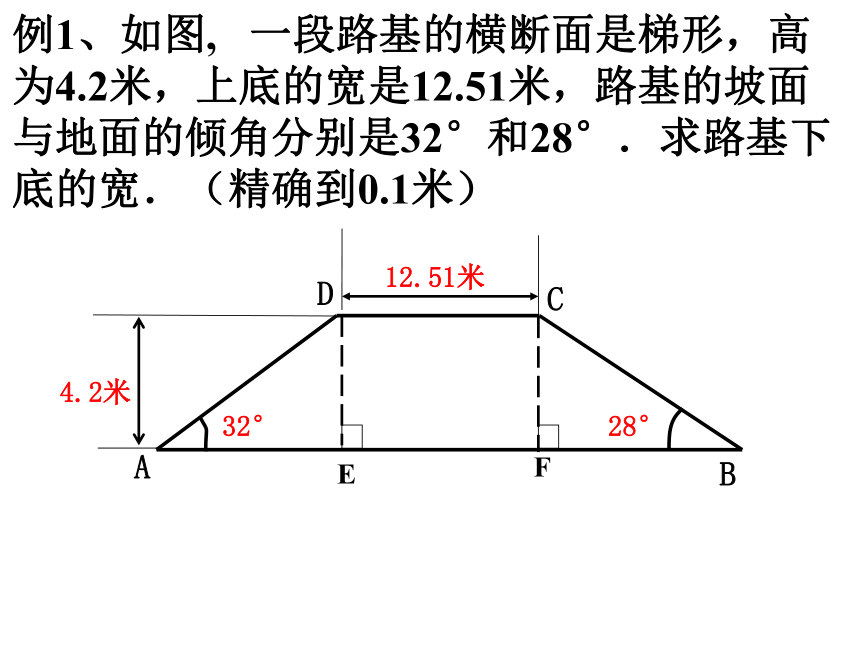
课件10张PPT。解直角三角形(3)问题回顾 在RtΔABC中，若∠C =900， 问题1. 两锐角∠A与∠B有什么关系?答： ∠A+ ∠B= 900.问题2. 三边a、b、c的关系如何？答：a2+b2 =c2.问题3. ∠B与边的关系是什么？答:例1、如图, 一段路基的横断面是梯形，高为4.2米，上底的宽是12.51米，路基的坡面与地面的倾角分别是32°和28°．求路基下底的宽．（精确到0.1米） 探索新知坡度通常写成1∶m的形式，如i=1∶6.坡面与水平面的夹角叫做坡角，记作a，有i＝ =tan a
显然，坡度越大，坡角a就越大，坡面就越陡.
在修路、挖河、开渠和筑坝时，设计图纸上都要注明斜坡的倾斜程度.
如图19.4.5，坡面的铅垂高度（h）和水平长度（l）
的比叫做坡面坡度（或坡比）.记作i,即i= .
例2.如图是某公路路基的设计简图,等腰梯形ABCD表示它的横断面,原计划设计的坡角为A=22°37′,坡长AD=6. 5米,现考虑到在短期内车流量会增加,需增加路面宽度,故改变设计方案,将图中1,2两部分分别补到3,4的位置,使横断面EFGH为等腰梯形,重新设计后路基的坡角为32°,全部工程的用土量不变,问:路面宽将增加多少?
(选用数据:sin22°37′≈ ,cos22°37′ ≈ ,
tan 22°37′ ≈ ,
tan 32° ≈ )MN试一试 1.两幢大楼相距110米，从甲楼顶部看乙楼顶部的仰角为26°，如果甲楼高35米，那么乙楼的高为多少米？（精确到1米） 2.一艘船向东航行，上午8时到达B处，看到有一灯塔在它的北偏东59°，距离为72海里的A处，上午10时到达C处，看到灯塔在它的正北方向．求这艘船航行的速度．（精确到1海里/时）答案:乙楼高约89米答案:这艘船航行的速度约31 海里/时小结: 1.在解直角三角形及应用时经常接触到的一些概念
2.实际问题向数学模型的转化
3.解直角三角形的边角关系
由于过度采伐森林和破坏植被，我国部分地区频频遭受沙尘暴侵袭。近日，A城气象局测得沙尘暴中心在A城的正南方向240km的B处，以每小时12km的速度向北偏东30°方向移动，距沙尘暴中心150km的范围为受影响区域。附加题（1）A城是否受到这次沙尘暴的影响，为什么？（2）若A城受这次沙尘暴的影响，那么遭受影响的时间有多长？解（1）：过A作AC⊥BM,垂足为C,在Rt△ABC中， ∠B = 30°, ∵AC = 120 < 150∴A城受到沙尘暴影响 由于过度采伐森林和破坏植被，我国部分地区频频遭受沙尘暴侵袭。近日，A城气象局测得沙尘暴中心在A城的正南方向240km的B处，以每小时12km的速度向北偏东30°方向移动，距沙尘暴中心150km的范围为受影响区域。附加题（1）A城是否受到这次沙尘暴的影响，为什么？（2）若A城受这次沙尘暴的影响，那么遭受影响的时间有多长？解（2）：设点E、F是以A为圆心，150km为半径的圆与BM的交点，由题意得：∴EF = 2CE = 2 x 90 = 180∴A城受到沙尘暴影响的时间为180÷12 = 15小时答：A城将受到这次沙尘暴影响，影响的时间为15小时。作业 1.教科书P 116. 习题 1. 2. 见作业本
3.教科书P 120 习题 B组.