§19.4 解直角三角形(第一课时)[下学期] 华东师大版[下学期]
文档属性
| 名称 | §19.4 解直角三角形(第一课时)[下学期] 华东师大版[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-05-22 11:43:00 | ||
图片预览




文档简介
课件16张PPT。§19.4 解直角三角形甘肃省金塔镇中学数学教师
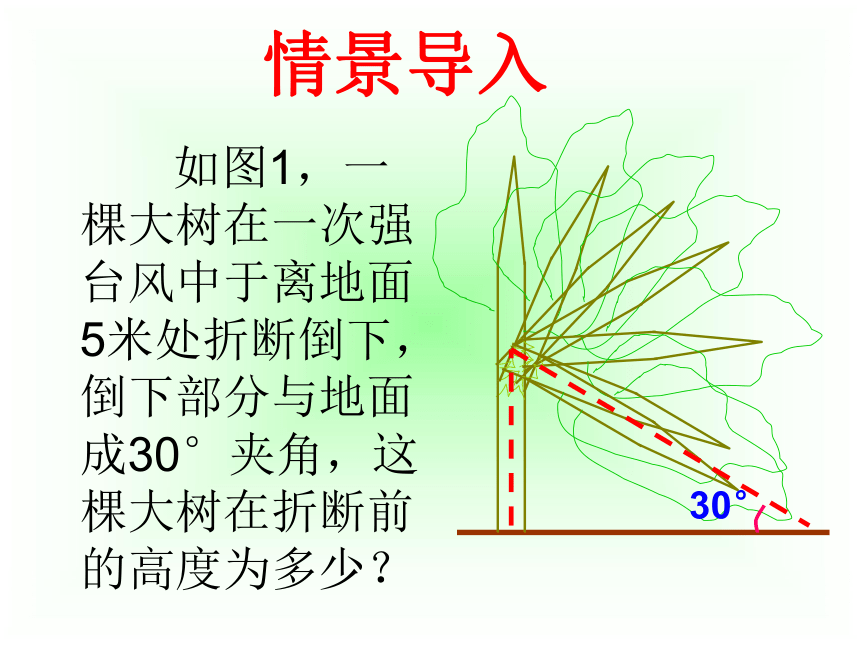
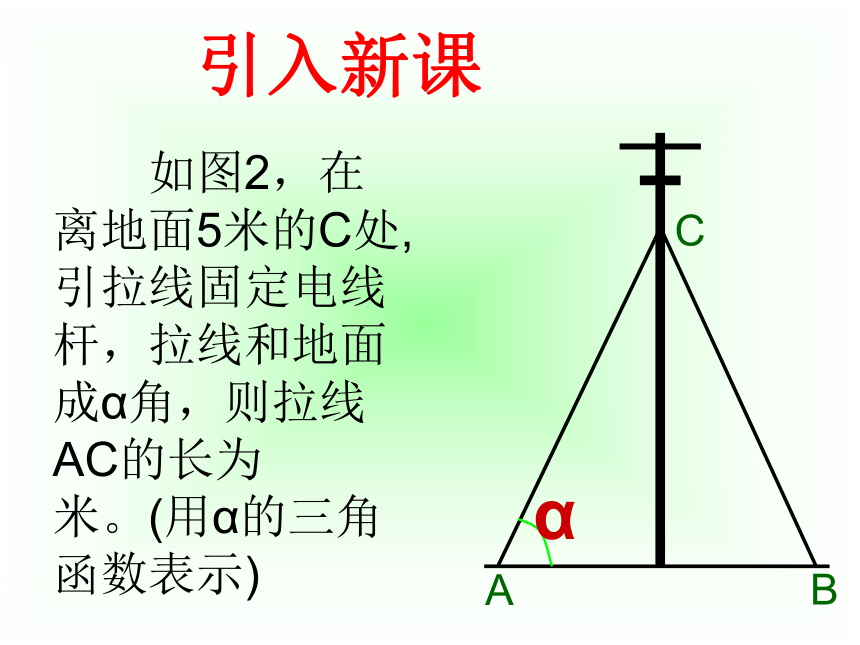
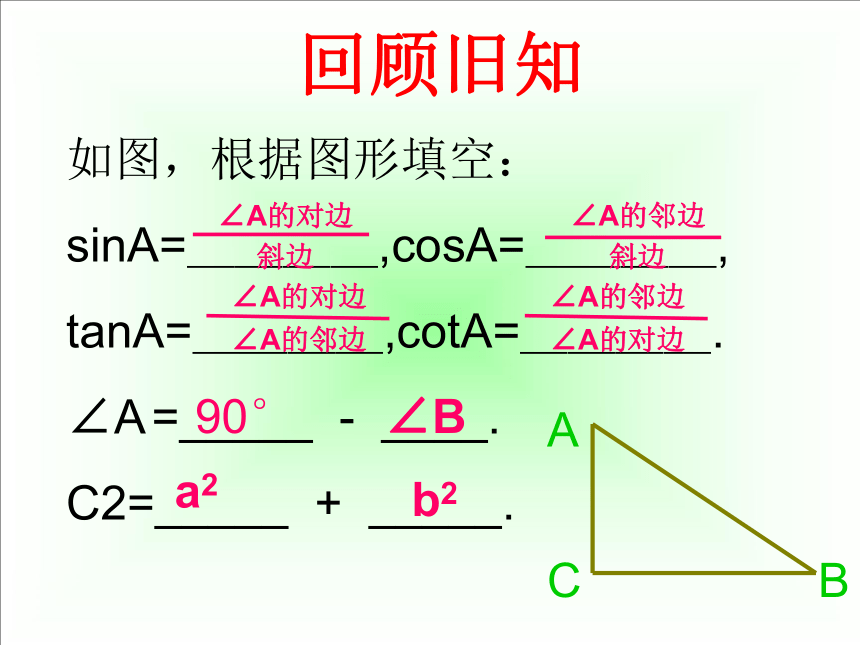
姜永齐情景导入 如图1,一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为多少? 引入新课 如图2,在离地面5米的C处,引拉线固定电线杆,拉线和地面成α角,则拉线AC的长为 米。(用α的三角函数表示)回顾旧知如图,根据图形填空:
sinA=____,cosA=____,
tanA=____,cotA=____.
∠A =_____ - ____.
C2=_____ + _____.90°∠Ba2b2情景分析 我们在遇到实际问题时,总是首先把新问题与我们熟悉的问题联系起来,再把新问题转化成熟悉的问题来进行研究.那么,怎样把这个实际问题变成我们熟悉的图形呢? 我们知道在直角三角形中已知一些元素,求另一些未知元素的方法.像这样的过程我们称之为解直角三角形.你知道了吗? 体验归纳 1.以上情景中的两个问题都可以利用直角三角形的边、角关系,以及锐角三角函数的知识来解决。 2.解直角三角形的含义:在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形。 合作探究 小组合作问题1:
你能否编一道“解直角三角形”的问题,让别的同学验证一下,看是否能求出其它元素?要求:1.小组之间相互汇报交流结果,其他组纠正,补充。
2.归纳解直角三角形的两种情况。小组合作问题2:
1.请你画图解释什么是方向角问题?并将你获得的结论与小组同学交流一下。
2.各小组汇总、归纳解题方法。明确: 1.对于现实总是通常化为数学模型来处理,这里体现数学建模的思想。2.会用锐角三角函数关系式解直角三角形。 问题解决 例:如图,东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米)归纳总结(1)内容总结:用锐角的三角函数关系式解直角三角形时,所求的边长通常作为分子比较好些。
(2)方法归纳:体验从实际生活中建立数学模型,运用直角三角形知识解决生活中的问题。
(3)说说你的收获。归纳总结解直角三角形的类型: 星级闯关 1.在RtΔABC中,∠C=90°,∠B=60°,a=4,解这个三角形。 2.(2005.南通)如图,为了测量一条河的宽度,一测量员在河岸边的C处测得对岸一棵树A在正南方向,测量员向正东方向走180m到点D处,测得这棵树在南偏西60°的方向,求河的宽度。(结果保留根号) 3.近日,A城气象局测得沙尘暴中心在A城的正西方向240公里的B处,正以每小时12公里的速度向北偏东60o的方向转移。距离沙尘暴中心150公里的范围为受影响区域。问:A城是否受这次沙尘暴的影响? 开拓思维回顾反思 1.小组代表发言总结本节学习的知识点和思想方法。2.你认为在利用解直角三角形解决一些实际问题时,应该注意什么?作业1. P113练习1、2题2. P116习题19.4- 1题
姜永齐情景导入 如图1,一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为多少? 引入新课 如图2,在离地面5米的C处,引拉线固定电线杆,拉线和地面成α角,则拉线AC的长为 米。(用α的三角函数表示)回顾旧知如图,根据图形填空:
sinA=____,cosA=____,
tanA=____,cotA=____.
∠A =_____ - ____.
C2=_____ + _____.90°∠Ba2b2情景分析 我们在遇到实际问题时,总是首先把新问题与我们熟悉的问题联系起来,再把新问题转化成熟悉的问题来进行研究.那么,怎样把这个实际问题变成我们熟悉的图形呢? 我们知道在直角三角形中已知一些元素,求另一些未知元素的方法.像这样的过程我们称之为解直角三角形.你知道了吗? 体验归纳 1.以上情景中的两个问题都可以利用直角三角形的边、角关系,以及锐角三角函数的知识来解决。 2.解直角三角形的含义:在直角三角形中,由已知元素求出未知元素的过程,叫做解直角三角形。 合作探究 小组合作问题1:
你能否编一道“解直角三角形”的问题,让别的同学验证一下,看是否能求出其它元素?要求:1.小组之间相互汇报交流结果,其他组纠正,补充。
2.归纳解直角三角形的两种情况。小组合作问题2:
1.请你画图解释什么是方向角问题?并将你获得的结论与小组同学交流一下。
2.各小组汇总、归纳解题方法。明确: 1.对于现实总是通常化为数学模型来处理,这里体现数学建模的思想。2.会用锐角三角函数关系式解直角三角形。 问题解决 例:如图,东西两炮台A、B相距2000米,同时发现入侵敌舰C,炮台A测得敌舰C在它的南偏东40゜的方向,炮台B测得敌舰C在它的正南方,试求敌舰与两炮台的距离.(精确到1米)归纳总结(1)内容总结:用锐角的三角函数关系式解直角三角形时,所求的边长通常作为分子比较好些。
(2)方法归纳:体验从实际生活中建立数学模型,运用直角三角形知识解决生活中的问题。
(3)说说你的收获。归纳总结解直角三角形的类型: 星级闯关 1.在RtΔABC中,∠C=90°,∠B=60°,a=4,解这个三角形。 2.(2005.南通)如图,为了测量一条河的宽度,一测量员在河岸边的C处测得对岸一棵树A在正南方向,测量员向正东方向走180m到点D处,测得这棵树在南偏西60°的方向,求河的宽度。(结果保留根号) 3.近日,A城气象局测得沙尘暴中心在A城的正西方向240公里的B处,正以每小时12公里的速度向北偏东60o的方向转移。距离沙尘暴中心150公里的范围为受影响区域。问:A城是否受这次沙尘暴的影响? 开拓思维回顾反思 1.小组代表发言总结本节学习的知识点和思想方法。2.你认为在利用解直角三角形解决一些实际问题时,应该注意什么?作业1. P113练习1、2题2. P116习题19.4- 1题
