解直角三角形复习(1)[下学期]
图片预览



文档简介
课件13张PPT。解直角三角形复习(1)
1。会利用相似三角形的性质进行测量2。会利用勾股定理解决实际问题3。理解三角函数的定义,熟记特殊角的三角函数值4。会运用三角函数探索直角三角形的边角关系并解
决实际问题一。学习目标三边关系1。2。在直角三角形中,如果一个锐角等于30゜,
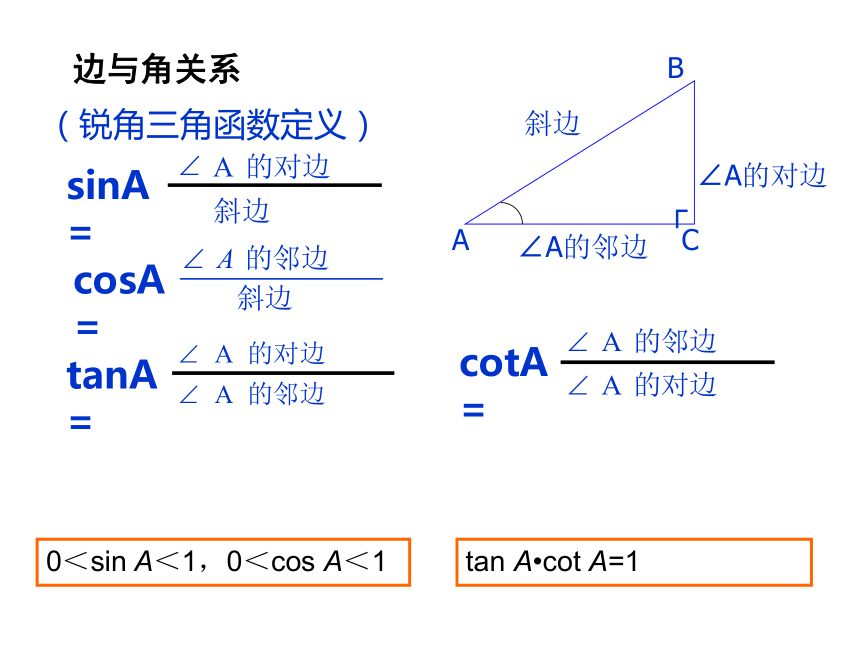
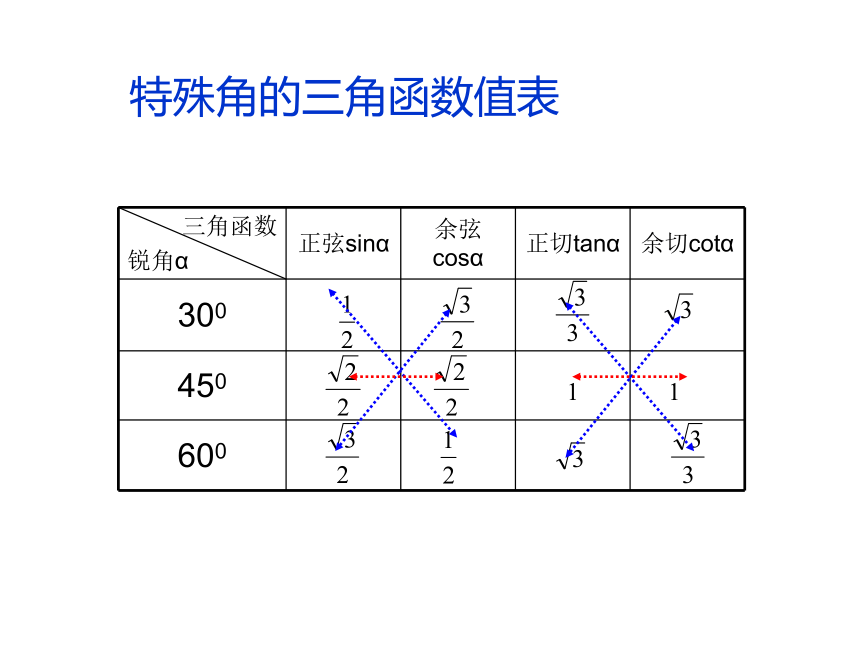
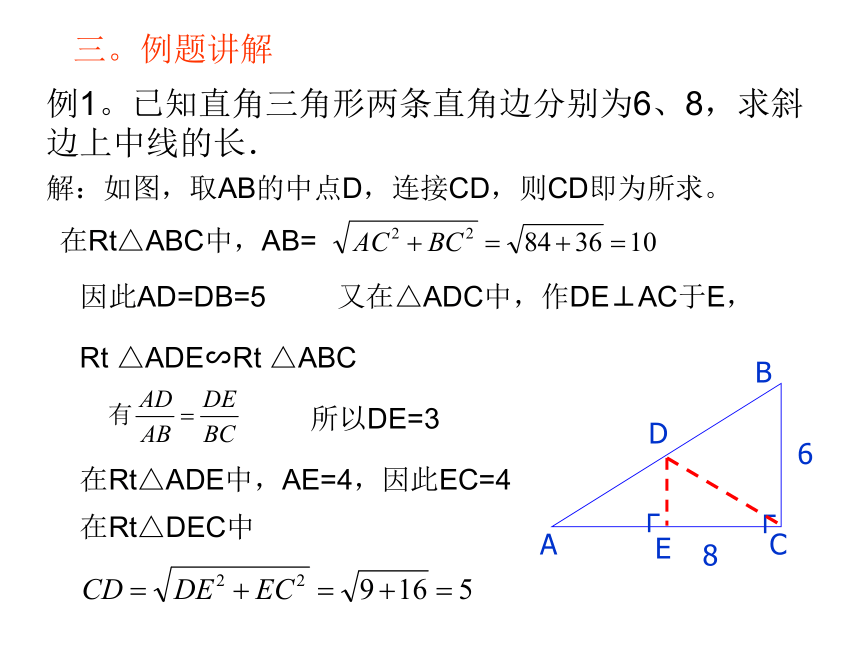
那么它所对的直角边等于斜边的一半.二,知识归纳(锐角三角函数定义)cosA=边与角关系0<sin A<1,0<cos A<1tan A?cot A=1 特殊角的三角函数值表三。例题讲解例1。已知直角三角形两条直角边分别为6、8,求斜
边上中线的长.ABC86┌DE┌解:如图,取AB的中点D,连接CD,则CD即为所求。又在△ADC中,作DE⊥AC于E,Rt △ADE∽Rt △ABC在Rt△ABC中,AB=因此AD=DB=5所以DE=3在Rt△ADE中,AE=4,因此EC=4在Rt△DEC中(1) y的值; (2) 角 的正弦值 AB解 : (1)作PA⊥ x轴于A,
PB⊥ y轴于B,有OA=3,而
(2)在Rt△OPA中由勾股定理可求得OP=5所以sin (1)阴影部分是正方形; 1。求下列阴影部分的面积:练习(2)阴影部分是长方形; (3)阴影部分是半圆2。如图,以Rt△ABC的三边向外作三个半圆,试探
索三个半圆的面积之间的关系.两个小半圆的面积的和等于大半圆的面积 3。求下列各直角三角形中字母的值. 4. 求下列各式的值(1) 2cos 30°+cot 60°-2tan 45°;105.小明放一个线长为125米的风筝,他的风筝线与水平
地面构成39°角.他的风筝有多高?(精确到1米)6.在Rt△ABC中,∠C=90°,∠A=60°,∠A平分
线AM的长为15 cm,求直角边AC和斜边AB的长.
79米 分析:解决此类实际问题的关键是画出正
确的示意图,能说出 题目中每句话对
应图中哪个角或边,将实际问题转化
直角三角形的问题来解决。 7.已知在Rt△ABC中,∠C=90°,直角边AC是直角
边BC的2倍,求∠B的四个三角函数值.
8.如图,飞机A在目标B的正上方1 000米处,飞行员测
得地面目标C的俯角为30°,求地面目标B、C之间的
距离.
2
决实际问题一。学习目标三边关系1。2。在直角三角形中,如果一个锐角等于30゜,
那么它所对的直角边等于斜边的一半.二,知识归纳(锐角三角函数定义)cosA=边与角关系0<sin A<1,0<cos A<1tan A?cot A=1 特殊角的三角函数值表三。例题讲解例1。已知直角三角形两条直角边分别为6、8,求斜
边上中线的长.ABC86┌DE┌解:如图,取AB的中点D,连接CD,则CD即为所求。又在△ADC中,作DE⊥AC于E,Rt △ADE∽Rt △ABC在Rt△ABC中,AB=因此AD=DB=5所以DE=3在Rt△ADE中,AE=4,因此EC=4在Rt△DEC中(1) y的值; (2) 角 的正弦值 AB解 : (1)作PA⊥ x轴于A,
PB⊥ y轴于B,有OA=3,而
(2)在Rt△OPA中由勾股定理可求得OP=5所以sin (1)阴影部分是正方形; 1。求下列阴影部分的面积:练习(2)阴影部分是长方形; (3)阴影部分是半圆2。如图,以Rt△ABC的三边向外作三个半圆,试探
索三个半圆的面积之间的关系.两个小半圆的面积的和等于大半圆的面积 3。求下列各直角三角形中字母的值. 4. 求下列各式的值(1) 2cos 30°+cot 60°-2tan 45°;105.小明放一个线长为125米的风筝,他的风筝线与水平
地面构成39°角.他的风筝有多高?(精确到1米)6.在Rt△ABC中,∠C=90°,∠A=60°,∠A平分
线AM的长为15 cm,求直角边AC和斜边AB的长.
79米 分析:解决此类实际问题的关键是画出正
确的示意图,能说出 题目中每句话对
应图中哪个角或边,将实际问题转化
直角三角形的问题来解决。 7.已知在Rt△ABC中,∠C=90°,直角边AC是直角
边BC的2倍,求∠B的四个三角函数值.
8.如图,飞机A在目标B的正上方1 000米处,飞行员测
得地面目标C的俯角为30°,求地面目标B、C之间的
距离.
2
