5.3圆的面积(课件)青岛版六年级上册数学(共36张PPT)
文档属性
| 名称 | 5.3圆的面积(课件)青岛版六年级上册数学(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 10:30:54 | ||
图片预览







文档简介
(共36张PPT)
五 完美的图形
——圆
5.3 圆的面积
学习目标
1.理解圆的面积计算公式的推导过程。(难点)
2.理解圆的面积和环形面积的意义,掌握圆的面积计算公式和环形面积的计算方法。(重点)
3.在自主解决问题的过程中,体验探索学习的乐趣。
情境导入
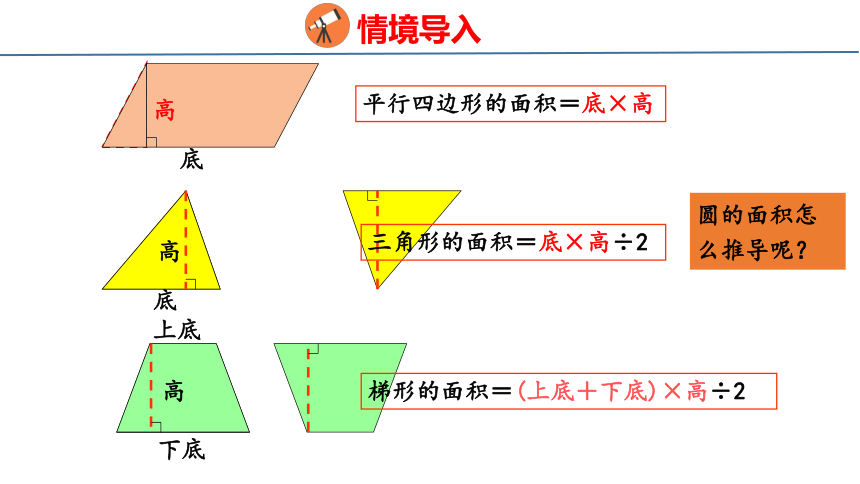
底
高
平行四边形的面积=底×高
高
底
三角形的面积=底×高÷2
下底
上底
高
上底
梯形的面积=(上底+下底)×高÷2
圆的面积怎么推导呢?
探索新知
你能提出什么问题?
探索新知
(教材P67 例1)
中心舞台的面积是多少平方米?
探索新知
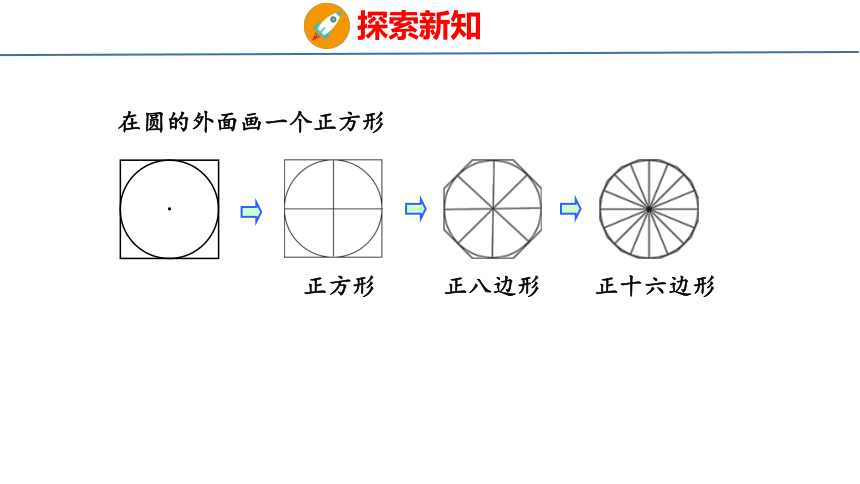
在圆的外面画一个正方形,圆的面积比正方形面积小一些。
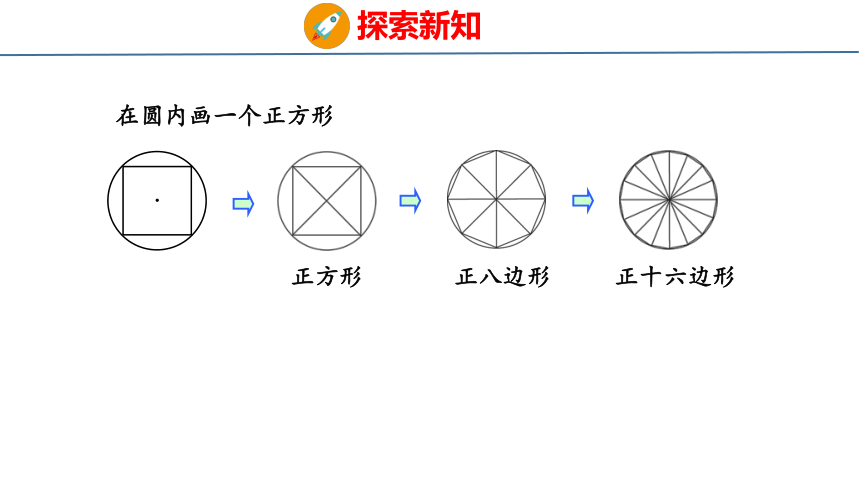
在圆内画一个正方形,圆的面积比正方形面积大一些。
方法一:把圆转化成正多边形来求圆的面积。
探索新知
正方形
正八边形
正十六边形
在圆的外面画一个正方形
探索新知
正方形
正八边形
正十六边形
在圆内画一个正方形
探索新知
正多边形的边数越多,它的面积越接近圆的面积。
所以只要求出正多边形的面积就可以得到圆的面积。
探索新知
推导圆的面积计算公式
先求出一个小三角形的面积,再乘小三角形的个数。
小三角
形的底
小三角
形的高
小三角形
的个数
探索新知
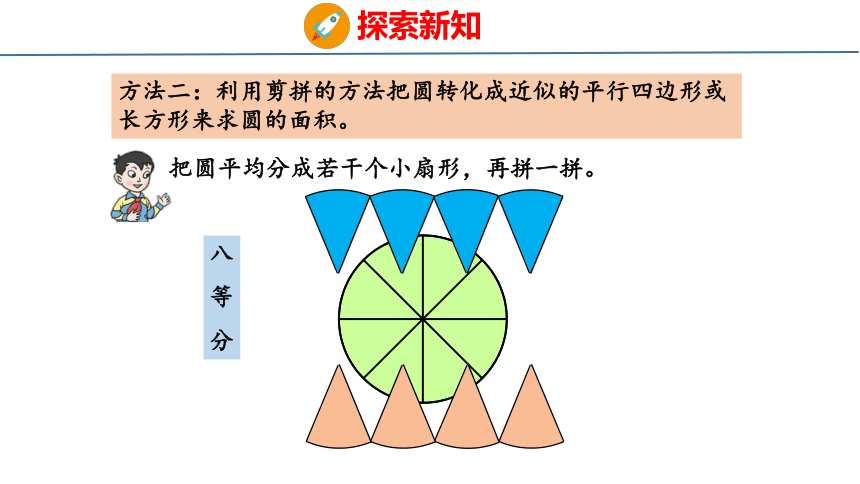
方法二:利用剪拼的方法把圆转化成近似的平行四边形或长方形来求圆的面积。
把圆平均分成若干个小扇形,再拼一拼。
八
等
分
探索新知
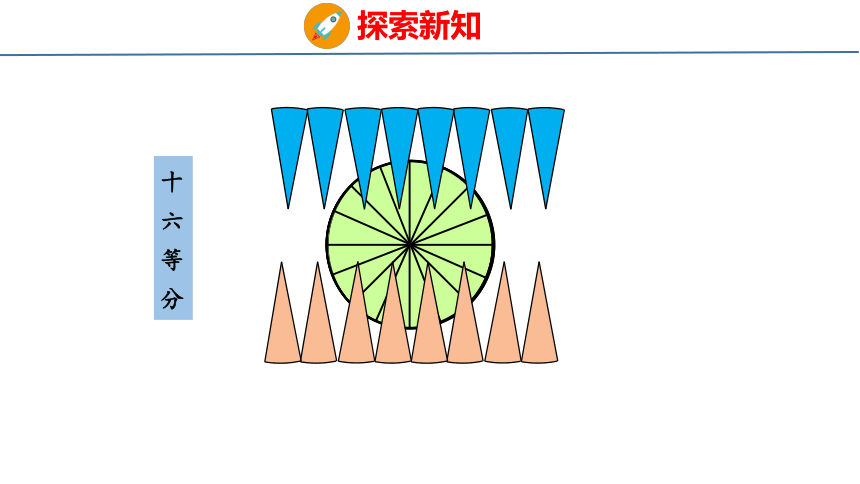
十六等分
探索新知
三
十
二
等
分
探索新知
曲
直
探索新知
…
平均分的份数越多,拼成的图形越接近于长方形。
探索新知
1
2
C
r
拼成的长方形的面积等于圆的面积。
探索新知
长方形的面积 = 长 × 宽
圆的面积
1
2
C
r
= ×
= × 2πr × r
1
2
= πr2
如果用S表示圆的面积,那么圆的面积计算公式可以写成
S=πr2
探索新知
答:中心舞台的面积是314平方米。
= 3.14×102
= 3.14×100
= 314(平方米)
3.14×
( )
2
20
2
中心舞台的面积是:
探索新知
下面图形的面积是多少平方厘米?
(教材P69 例2)
12cm
20cm
环形面积=外圆面积-内圆面积。
探索新知
12cm
20cm
=3.14×102
3.14×62
-
=3.14×100
-
3.14×36
=200.96(平方厘米)
答:这个图形的面积是200.96平方厘米。
-
3.14×
( )
2
20
2
3.14×
( )
2
12
2
1.(教材P69 自主练习 第1题)
随堂小练
求下面各圆的面积。
3.14×52
3.14×22
= 3.14×4
= 12.56(m2)
= 3.14×100
= 314(mm2)
= 3.14×25
= 78.5(dm2)
3.14×
( )
2
20
2
2.(教材P70 自主练习 第2题)
随堂小练
如图,一个圆形小岛的直径是50米。它的占地面积是多少平方米?
3.14×( 50÷2) = 1962.5(平方米)
答:它的占地面积是1962.5平方米。
3.(教材P70 自主练习 第3题)
随堂小练
这个自动旋转喷水器的喷灌面积是多少平方米?
3.14×8 = 200.96(平方米)
答:这个自动旋转喷水器的喷灌面积是200.96平方米。
4.(教材P70 自主练习 第4题)
随堂小练
(1)如果把图中这片荷叶看作圆形,它的面积有多大?
(2)你还见过哪些近似于圆形的叶子?先估一估它们的面积,再算一算。
3.14×(40÷2) = 1256( cm )
自己做一做。
5.(教材P70 自主练习 第5题)
随堂小练
用一张长方形铁板(如右图)切割出一个最大的圆。
(1)圆的面积是多少平方米?
(2)剩余部分的面积是多少平方米?
3.14×(2÷2) =3.14(平方米)
3×2-3.14=2.86(平方米)
当堂检测
1.(教材P70 自主练习 第6题)
将表格填完整。
6
18.84
28.26
4
25.12
50.24
3
1.5
7.065
当堂检测
2.(教材P70 自主练习 第7题)
一个圆形桌面的直径是2米。
(1)如果要给桌面铺上与它同样大小的玻璃,这块玻璃的面积是多少平方米?
(2)如果在桌面的周围镶上金属条,需要多少米?
3.14×(2÷2) =3.14(平方米)
3.14x2=6.28(米)
当堂检测
3.(教材P71 自主练习 第8题)
计算下面各图涂色部分的面积。
半圆面积:
3.14×(10÷2)2÷2
=39.25(dm )
三角形面积:
10×5÷2=25(dm )
39.25-25=14.25(dm )
涂色部分面积:
当堂检测
3.14×( 7 -4 )= 103.62(dm )
40×40=1600(cm )
3.14×( 40÷2) =1256(cm )
1600-1256=344(cm )
当堂检测
4.(教材P71 自主练习 第9题)
下图是清代的一枚铜钱及其示意图。算出示意图中涂色部分的面积大约是多少平方厘米。(得数保留一位小数)
3.14×( 3÷2) -0.8×0.8≈6.4(平方厘米)
当堂检测
5.(教材P71 自主练习 第10题)
一个圆形旱冰场的直径是30米,扩建后半径增加了5米。扩建后旱冰场的面积增加了多少平方米?
3.14×(30÷2+5)2-3.14×(30÷2)2
= 1256-706.5
= 549.5(平方米)
当堂检测
6.(教材P71 自主练习 第11题)
想一想,填一填。
152=225 452=2025 752=( )
252=625 552=3025 852=( )
352=1225 652=( ) 952=( )
4225
5625
7225
9025
你发现了什么规律?与同学交流一下。
规律:个位上是5的两个相同的两位数相乘,积的末两位是25,25前面的数是两位数十位上的数与比它大1的数的积。
当堂检测
7.(教材P71 自主练习 第12题)
涂色部分的周长和面积各是多少?
思路分析:涂色部分的周长就是大圆的周长,面积就是大圆面积的一半。
周长:3.14×0.8=2.512( m)
面积:3.14×( 0.8÷2) ÷2=0.2512(m )
学习完本节课,你有什么收获?
课堂小结
课堂小结
1.圆的面积公式
2.环形面积的计算
环形面积计算公式:
S=πR -πr
=π(R -r )
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
五 完美的图形
——圆
5.3 圆的面积
学习目标
1.理解圆的面积计算公式的推导过程。(难点)
2.理解圆的面积和环形面积的意义,掌握圆的面积计算公式和环形面积的计算方法。(重点)
3.在自主解决问题的过程中,体验探索学习的乐趣。
情境导入
底
高
平行四边形的面积=底×高
高
底
三角形的面积=底×高÷2
下底
上底
高
上底
梯形的面积=(上底+下底)×高÷2
圆的面积怎么推导呢?
探索新知
你能提出什么问题?
探索新知
(教材P67 例1)
中心舞台的面积是多少平方米?
探索新知
在圆的外面画一个正方形,圆的面积比正方形面积小一些。
在圆内画一个正方形,圆的面积比正方形面积大一些。
方法一:把圆转化成正多边形来求圆的面积。
探索新知
正方形
正八边形
正十六边形
在圆的外面画一个正方形
探索新知
正方形
正八边形
正十六边形
在圆内画一个正方形
探索新知
正多边形的边数越多,它的面积越接近圆的面积。
所以只要求出正多边形的面积就可以得到圆的面积。
探索新知
推导圆的面积计算公式
先求出一个小三角形的面积,再乘小三角形的个数。
小三角
形的底
小三角
形的高
小三角形
的个数
探索新知
方法二:利用剪拼的方法把圆转化成近似的平行四边形或长方形来求圆的面积。
把圆平均分成若干个小扇形,再拼一拼。
八
等
分
探索新知
十六等分
探索新知
三
十
二
等
分
探索新知
曲
直
探索新知
…
平均分的份数越多,拼成的图形越接近于长方形。
探索新知
1
2
C
r
拼成的长方形的面积等于圆的面积。
探索新知
长方形的面积 = 长 × 宽
圆的面积
1
2
C
r
= ×
= × 2πr × r
1
2
= πr2
如果用S表示圆的面积,那么圆的面积计算公式可以写成
S=πr2
探索新知
答:中心舞台的面积是314平方米。
= 3.14×102
= 3.14×100
= 314(平方米)
3.14×
( )
2
20
2
中心舞台的面积是:
探索新知
下面图形的面积是多少平方厘米?
(教材P69 例2)
12cm
20cm
环形面积=外圆面积-内圆面积。
探索新知
12cm
20cm
=3.14×102
3.14×62
-
=3.14×100
-
3.14×36
=200.96(平方厘米)
答:这个图形的面积是200.96平方厘米。
-
3.14×
( )
2
20
2
3.14×
( )
2
12
2
1.(教材P69 自主练习 第1题)
随堂小练
求下面各圆的面积。
3.14×52
3.14×22
= 3.14×4
= 12.56(m2)
= 3.14×100
= 314(mm2)
= 3.14×25
= 78.5(dm2)
3.14×
( )
2
20
2
2.(教材P70 自主练习 第2题)
随堂小练
如图,一个圆形小岛的直径是50米。它的占地面积是多少平方米?
3.14×( 50÷2) = 1962.5(平方米)
答:它的占地面积是1962.5平方米。
3.(教材P70 自主练习 第3题)
随堂小练
这个自动旋转喷水器的喷灌面积是多少平方米?
3.14×8 = 200.96(平方米)
答:这个自动旋转喷水器的喷灌面积是200.96平方米。
4.(教材P70 自主练习 第4题)
随堂小练
(1)如果把图中这片荷叶看作圆形,它的面积有多大?
(2)你还见过哪些近似于圆形的叶子?先估一估它们的面积,再算一算。
3.14×(40÷2) = 1256( cm )
自己做一做。
5.(教材P70 自主练习 第5题)
随堂小练
用一张长方形铁板(如右图)切割出一个最大的圆。
(1)圆的面积是多少平方米?
(2)剩余部分的面积是多少平方米?
3.14×(2÷2) =3.14(平方米)
3×2-3.14=2.86(平方米)
当堂检测
1.(教材P70 自主练习 第6题)
将表格填完整。
6
18.84
28.26
4
25.12
50.24
3
1.5
7.065
当堂检测
2.(教材P70 自主练习 第7题)
一个圆形桌面的直径是2米。
(1)如果要给桌面铺上与它同样大小的玻璃,这块玻璃的面积是多少平方米?
(2)如果在桌面的周围镶上金属条,需要多少米?
3.14×(2÷2) =3.14(平方米)
3.14x2=6.28(米)
当堂检测
3.(教材P71 自主练习 第8题)
计算下面各图涂色部分的面积。
半圆面积:
3.14×(10÷2)2÷2
=39.25(dm )
三角形面积:
10×5÷2=25(dm )
39.25-25=14.25(dm )
涂色部分面积:
当堂检测
3.14×( 7 -4 )= 103.62(dm )
40×40=1600(cm )
3.14×( 40÷2) =1256(cm )
1600-1256=344(cm )
当堂检测
4.(教材P71 自主练习 第9题)
下图是清代的一枚铜钱及其示意图。算出示意图中涂色部分的面积大约是多少平方厘米。(得数保留一位小数)
3.14×( 3÷2) -0.8×0.8≈6.4(平方厘米)
当堂检测
5.(教材P71 自主练习 第10题)
一个圆形旱冰场的直径是30米,扩建后半径增加了5米。扩建后旱冰场的面积增加了多少平方米?
3.14×(30÷2+5)2-3.14×(30÷2)2
= 1256-706.5
= 549.5(平方米)
当堂检测
6.(教材P71 自主练习 第11题)
想一想,填一填。
152=225 452=2025 752=( )
252=625 552=3025 852=( )
352=1225 652=( ) 952=( )
4225
5625
7225
9025
你发现了什么规律?与同学交流一下。
规律:个位上是5的两个相同的两位数相乘,积的末两位是25,25前面的数是两位数十位上的数与比它大1的数的积。
当堂检测
7.(教材P71 自主练习 第12题)
涂色部分的周长和面积各是多少?
思路分析:涂色部分的周长就是大圆的周长,面积就是大圆面积的一半。
周长:3.14×0.8=2.512( m)
面积:3.14×( 0.8÷2) ÷2=0.2512(m )
学习完本节课,你有什么收获?
课堂小结
课堂小结
1.圆的面积公式
2.环形面积的计算
环形面积计算公式:
S=πR -πr
=π(R -r )
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
