§19.4 解直角三角形复习[下学期] 华师大版[下学期]
文档属性
| 名称 | §19.4 解直角三角形复习[下学期] 华师大版[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 276.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-05-29 00:00:00 | ||
图片预览




文档简介
课件17张PPT。 解直角三角形 综合练习金塔镇中学 姜永齐三边之间的关系a2+b2=c2(勾股定理);锐角之间的关系∠ A+ ∠ B= 90o边角之间的关系sinA=解直角三角形的依据1、2、特殊角度的三角函数值cosααsinαtanαcotα30o45o60o4、在0o到90o之间,三角函数值随着角度的变化而发生怎样的变化?答:在0o到90o之间, sinα 随着∠ α的增大而增大;3、四个锐角三角函数的取值范围5、同角锐角三角函数之间的关系0000cosα 随着∠ α的增大而减小;tanα 随着∠ α的增大而增大;cotα 随着∠ α的增大而减小;sin2α + cos2α = 1 tanα ? cotα = 16、互余两角三角函数之间的关系 sinA = cos(90o-A) cosA = sin(90o-A)
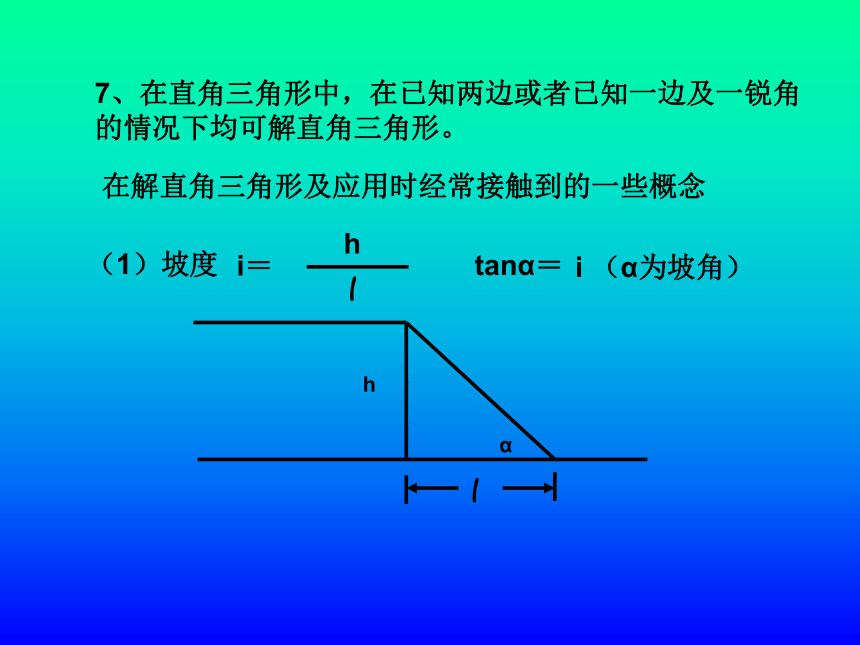
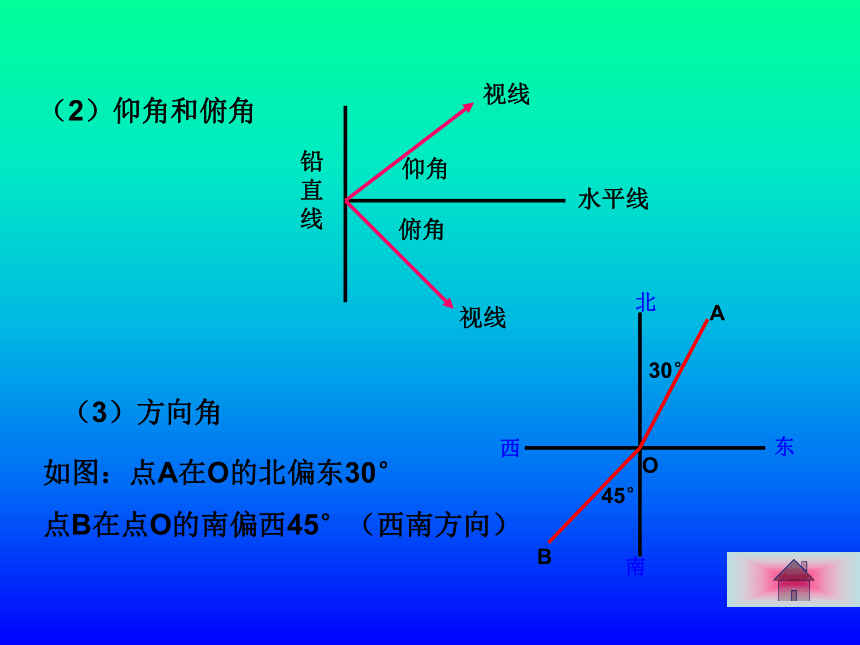
tanA = cot(90o-A) cotA = tan(90o-A) 例 1(1)计算:cos60o- cot45o+3tan60o-sin30o(2)化简:| sinA | - | sinA – 1 | (3)已知 △ABC中, | 2sinA – 1 | + ( 2 cosB- )2 =0试判断△ABC的形状。7、在直角三角形中,在已知两边或者已知一边及一锐角的情况下均可解直角三角形。在解直角三角形及应用时经常接触到的一些概念(2)仰角和俯角铅直线水平线视线视线仰角俯角(3)方向角如图:点A在O的北偏东30°
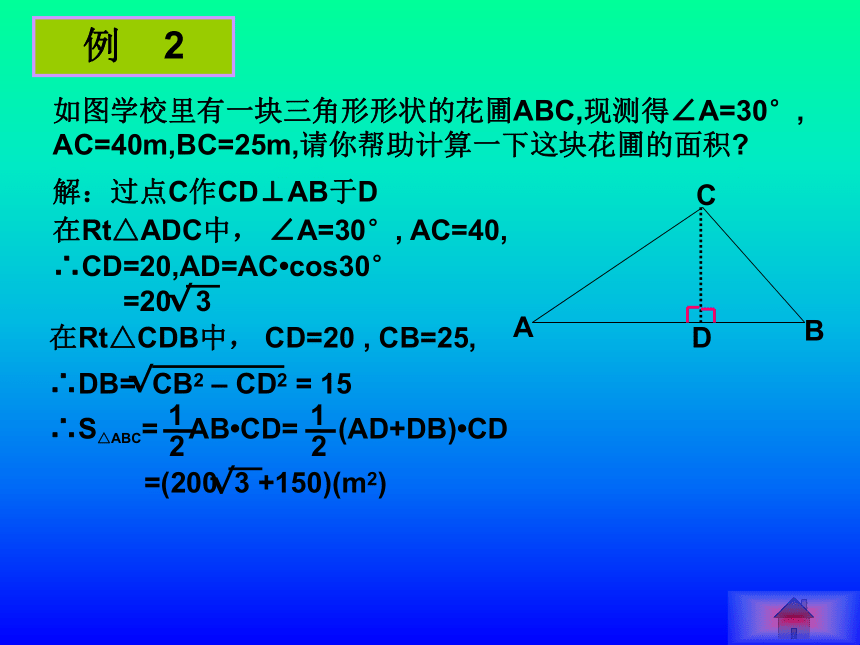
点B在点O的南偏西45°(西南方向)例 2如图学校里有一块三角形形状的花圃ABC,现测得∠A=30°, AC=40m,BC=25m,请你帮助计算一下这块花圃的面积?D解:过点C作CD⊥AB于D在Rt△ADC中, ∠A=30°, AC=40,∴CD=20,AD=AC?cos30°在Rt△CDB中, CD=20 , CB=25, 如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60?,航行24海里到C,见岛A在北偏西30?,货轮继续向西航行,有无触礁的危险?答:货轮无触礁危险。∵ ∠NBA= 60?, ∠N1BA= 30?,∴ ∠ABC=30?, ∠ACD= 30?,在Rt△ADC中, CD=AD?cot∠ACD= x?cot60?, 在Rt△ADB中, BD=AD?cot30?= x?cot30?, ∵ BD-CD=BC,BC=24 ∴ x?cot30?- x?cot60?=24 ≈12×1.732 =20.784 > 20 解:过点A作AD⊥BC于D,设AD=x例 3 由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。例 4(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?解(1):过A作AC⊥BM,垂足为C,在Rt△ABC中, ∠B = 30°, ∵AC = 120 < 150∴A城受到沙尘暴影响 由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。例 4(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?解(2):设点E、F是以A为圆心,150km为半径的圆与BM的交点,由题意得:∴EF = 2CE = 2 x 90 = 180∴A城受到沙尘暴影响的时间为180÷12 = 15小时答:A城将受到这次沙尘暴影响,影响的时间为15小时。1、本节例题学习以后,我们可以得到解直角三角形的两种基本图形:小结:2、 现实对象 数学模型 实际问题的解 数学问题的解 数学抽象 逻辑推理 翻译回去 有无解? 思考题 某班数学兴趣小组同学打算去测量一铁塔的高度,他们带了以下工具?皮尺一根?教学三角板一副?高度为1.5米的测角仪(能测仰角和俯角的仪器)一架。 请帮助他们选择两种测量工具,并设计方案,写出必需的测量数据(用字母表示),画出测量图形,并用测量数据(用字母表示)写出计算铁塔高度的算式。(2)示意图如右图(3)CD=a ,BD=b方案1? ? 某班数学兴趣小组同学打算去测量一铁塔的高度,他们带了以下工具?皮尺一根?教学三角板一副?高度为1.5米的测角仪(能测仰角和俯角的仪器)一架。 请帮助他们选择两种测量工具,并设计方案,写出必需的测量数据(用字母表示),并画出测量图形,并用测量数据(用字母表示)写出计算铁塔高度的算式。(2)示意图如右图(3)BD=a , ∠ACE=?(4)AB = a tan?+ 1.5方案2? ?思考题 某班数学兴趣小组同学打算去测量一铁塔的高度,他们带了以下工具?皮尺一根?教学三角板一副?高度为1.5米的测角仪(能测仰角和俯角的仪器)一架。?若测量的铁塔位于小河的对岸,假如人又无法直接到达对岸,该如何设计测量方案?(2)示意图如右图(3)CD=1.5 ,DF=a方案3? ?思考题 某班数学兴趣小组同学打算去测量一铁塔的高度,他们带了以下工具?皮尺一根?教学三角板一副?高度为1.5米的测角仪(能测仰角和俯角的仪器)一架。
?若测量的铁塔位于小河的对岸,假如人又无法直接到达对岸,该如何设计测量方案?(2)示意图如右图(3)CD=b ,DF=a方案4? ?(4)思考题课外作业一课双测76页课后测试再 见
tanA = cot(90o-A) cotA = tan(90o-A) 例 1(1)计算:cos60o- cot45o+3tan60o-sin30o(2)化简:| sinA | - | sinA – 1 | (3)已知 △ABC中, | 2sinA – 1 | + ( 2 cosB- )2 =0试判断△ABC的形状。7、在直角三角形中,在已知两边或者已知一边及一锐角的情况下均可解直角三角形。在解直角三角形及应用时经常接触到的一些概念(2)仰角和俯角铅直线水平线视线视线仰角俯角(3)方向角如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向)例 2如图学校里有一块三角形形状的花圃ABC,现测得∠A=30°, AC=40m,BC=25m,请你帮助计算一下这块花圃的面积?D解:过点C作CD⊥AB于D在Rt△ADC中, ∠A=30°, AC=40,∴CD=20,AD=AC?cos30°在Rt△CDB中, CD=20 , CB=25, 如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60?,航行24海里到C,见岛A在北偏西30?,货轮继续向西航行,有无触礁的危险?答:货轮无触礁危险。∵ ∠NBA= 60?, ∠N1BA= 30?,∴ ∠ABC=30?, ∠ACD= 30?,在Rt△ADC中, CD=AD?cot∠ACD= x?cot60?, 在Rt△ADB中, BD=AD?cot30?= x?cot30?, ∵ BD-CD=BC,BC=24 ∴ x?cot30?- x?cot60?=24 ≈12×1.732 =20.784 > 20 解:过点A作AD⊥BC于D,设AD=x例 3 由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。例 4(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?解(1):过A作AC⊥BM,垂足为C,在Rt△ABC中, ∠B = 30°, ∵AC = 120 < 150∴A城受到沙尘暴影响 由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。例 4(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?解(2):设点E、F是以A为圆心,150km为半径的圆与BM的交点,由题意得:∴EF = 2CE = 2 x 90 = 180∴A城受到沙尘暴影响的时间为180÷12 = 15小时答:A城将受到这次沙尘暴影响,影响的时间为15小时。1、本节例题学习以后,我们可以得到解直角三角形的两种基本图形:小结:2、 现实对象 数学模型 实际问题的解 数学问题的解 数学抽象 逻辑推理 翻译回去 有无解? 思考题 某班数学兴趣小组同学打算去测量一铁塔的高度,他们带了以下工具?皮尺一根?教学三角板一副?高度为1.5米的测角仪(能测仰角和俯角的仪器)一架。 请帮助他们选择两种测量工具,并设计方案,写出必需的测量数据(用字母表示),画出测量图形,并用测量数据(用字母表示)写出计算铁塔高度的算式。(2)示意图如右图(3)CD=a ,BD=b方案1? ? 某班数学兴趣小组同学打算去测量一铁塔的高度,他们带了以下工具?皮尺一根?教学三角板一副?高度为1.5米的测角仪(能测仰角和俯角的仪器)一架。 请帮助他们选择两种测量工具,并设计方案,写出必需的测量数据(用字母表示),并画出测量图形,并用测量数据(用字母表示)写出计算铁塔高度的算式。(2)示意图如右图(3)BD=a , ∠ACE=?(4)AB = a tan?+ 1.5方案2? ?思考题 某班数学兴趣小组同学打算去测量一铁塔的高度,他们带了以下工具?皮尺一根?教学三角板一副?高度为1.5米的测角仪(能测仰角和俯角的仪器)一架。?若测量的铁塔位于小河的对岸,假如人又无法直接到达对岸,该如何设计测量方案?(2)示意图如右图(3)CD=1.5 ,DF=a方案3? ?思考题 某班数学兴趣小组同学打算去测量一铁塔的高度,他们带了以下工具?皮尺一根?教学三角板一副?高度为1.5米的测角仪(能测仰角和俯角的仪器)一架。
?若测量的铁塔位于小河的对岸,假如人又无法直接到达对岸,该如何设计测量方案?(2)示意图如右图(3)CD=b ,DF=a方案4? ?(4)思考题课外作业一课双测76页课后测试再 见
