解直角三角形[下学期]
图片预览



文档简介
课件17张PPT。
解直角三角形(2)
一、教学目标:
知识目标:了解测量中的仰角、俯角等概念;会运用三角函数、直角三角形的知识解决与仰角、俯角有关的简单的实际问题。
能力目标:培养学生解决实际问题的能力,增强应用数学的意识。
情感目标:在自主学习、不断探索中享受成功的喜悦,体验学以致用的乐趣。
二、教学重点:
运用解直角三角形知识解决与仰角、俯角有关的实际问题
三、教学难点:
如何把实际问题转化为数学问题
四、学情分析:
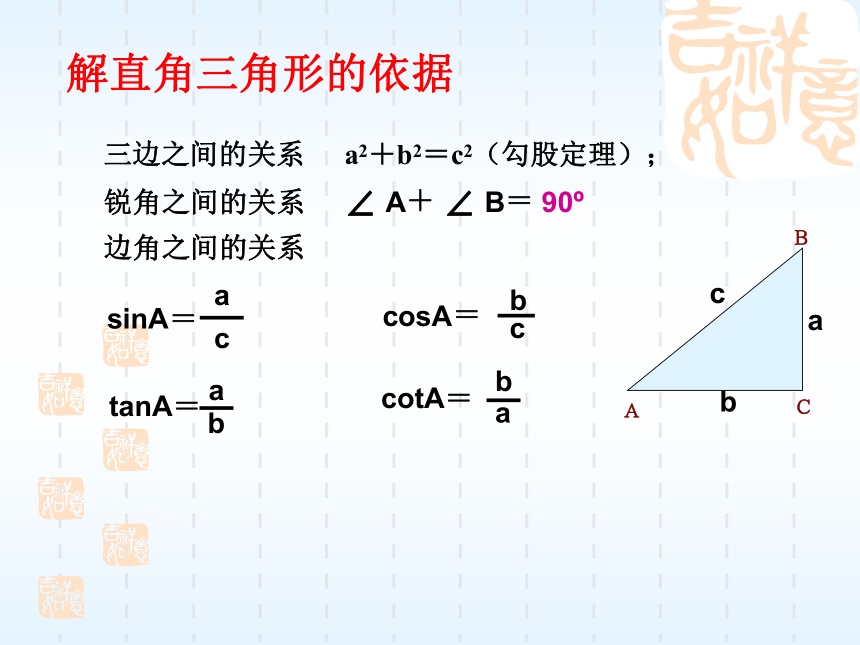
本节课的主要内容是让学生学会建筑物等的测量,然后根据所得到的数据进行计算,从而知道所测物体的高度或长度,在教学中应该让学生对测量方法有一定的掌握。三边之间的关系a2+b2=c2(勾股定理);锐角之间的关系∠ A+ ∠ B= 90o边角之间的关系sinA=解直角三角形的依据(1)仰角和俯角铅垂线水平线视线视线仰角俯角(2)方向角如图:点A在O的北偏东30°
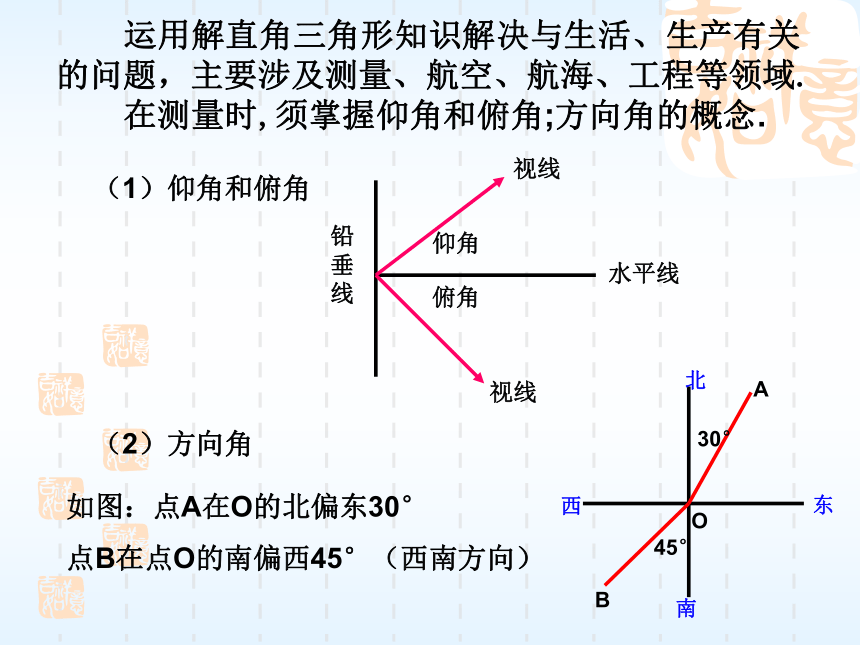
点B在点O的南偏西45°(西南方向) 运用解直角三角形知识解决与生活、生产有关的问题,主要涉及测量、航空、航海、工程等领域.
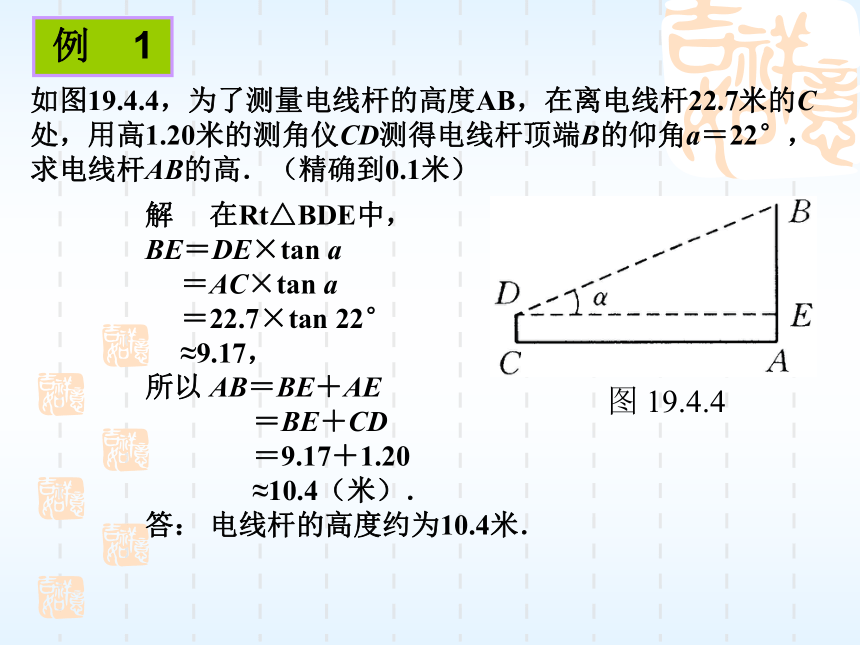
在测量时,须掌握仰角和俯角;方向角的概念.例 1解 在Rt△BDE中,
BE=DE×tan a
=AC×tan a
=22.7×tan 22°
≈9.17,
所以 AB=BE+AE
=BE+CD
=9.17+1.20
≈10.4(米).
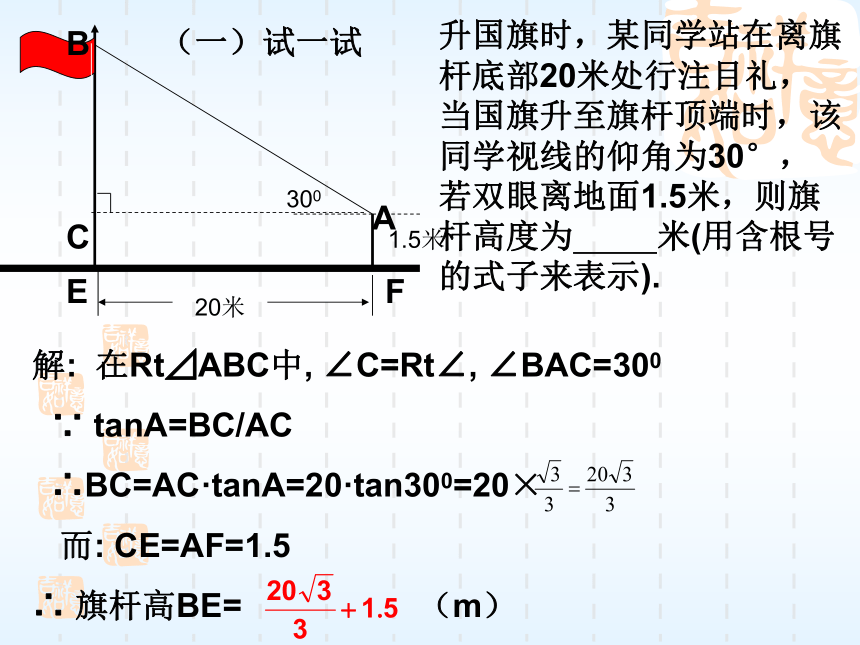
答: 电线杆的高度约为10.4米.如图19.4.4,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)30020米1.5米解: 在Rt⊿ABC中, ∠C=Rt∠, ∠BAC=300
∵ tanA=BC/AC
∴BC=AC·tanA=20·tan300=20×
而: CE=AF=1.5
∴ 旗杆高BE= (m)升国旗时,某同学站在离旗杆底部20米处行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角为30°,若双眼离地面1.5米,则旗杆高度为 米(用含根号的式子来表示).(一)试一试(二)你行吗?【例1】天空中有一个静止的广告气球C,从地面A点测得C的仰角为45°,从地面B点测得C点的仰角为60°,已知AB=20m,点C和直线AB在同一铅垂平面上,求气球离地面的高度?(结果保留根号)解:作CD⊥AB,垂足为D。设BD=x
在Rt⊿BCD中,CD=BD·tan∠CBD
=X·tan600=∵AD-BD=AB=20,即:∴气球离地面的高度为:在Rt⊿ACD中,AD=CD·cot∠DAC
= ·cot450=练一练1.如图所示,为了测量河对岸的旗杆AB的高度,在点C处测得旗杆顶端A的仰角为30°,沿CB方向前进5米到达D处,在D处测得旗杆顶端A的仰角为45°,
则旗杆AB的高度是 米。方法提炼:已知在RtΔABC中
∠ABC=90o,∠ACB=α,
∠ADB=β,AB=h,CD=a。
则:
在RtΔABC中,BC=AB?cotα
在RtΔADB中,DB=AB?cotβ
CB - DB=AB(cotα- cotβ)
所以:如图湖泊的中央有一个建筑物AB,某人在地面C处测得其顶部A的仰角为60o,然后自C处沿BC方向行100m至D处,又测得其顶部A的仰角为30o,求建筑物AB的高度。在山顶上处D有一铁塔,在塔顶B处测得地面上一点A的俯角α=60o,在塔底D测得点A的俯角β=45o,已知塔高BD=30米,求山高CD。ABCDαβ例 2(三)练一练 解:作BC⊥AM,垂足为C.
在Rt⊿ABC中,AB=28×1/2=14
∠BCA=900, ∠CAB=300
∴BC=AB·sin∠CAB
=14·sin300=14×1/2=7
∴ ∠1=600 ∠2=300在Rt⊿BCM中,BC=7 ∠CBM=∠2+150=450,
∴∠M=900- ∠CBM=450 ∴ CM=BC=7 答:船与灯塔的距离为:【例3】某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处,经16小时的航行到达,到达后必须立即卸货.此时,接到气象部门通知,一台风中心正以40海里/时的速度由A向北偏西60°方向移动,距台风中心200海里的圆形区域(包括边界)均会受到影响.
(1)问:B处是否会受到台风的影响?请说明理由.
(2)为避免受到台风的影响,该船应在多少小时内卸完货物?(供选用数据:(四)挑战自我【解析】(1)B处是否会受到台风的影响,只要求出点B
到AC的最短距离与台风中心半径相比较即可,故应过B
作BD⊥AC于 D.AB=20×16=320,∠CAB=30°?BD=160
<200 ∴B处受台风中心影响.(2)台风对B处若有影响,则B处到台风中心的距离不大
于200海里,则BE≤200,则DE=120,AD= 160 要在台风
到来之前卸完货物,必须在 2.如图所示,挂着“庆祝国庆”条幅的氢气球升在广场上空,已知气球的半径为2m,在地面A点测得气球中心O的仰角为60°,测得气球的视角
∠BAC=2°(B、C是⊙O上的点,
且OB⊥AB,OC⊥AC),则气球
中心O离地面的高度OD为( )
(sin 1°=0.0175,
结果精确到1m)
A.94m B.95m
C.99m D.105mC1.把实际问题转化成数学问题,这个转化为两个方面:一是将实际问题的图形转化为几何图形,画出正确的平面示意图,二是将已知条件转化为示意图中的边、角或它们之间的关系.2.把数学问题转化成解直角三角形问题,如果示意图不是
直角三角形,可添加适当的辅助线,画出直角三角形.方法小结:
解直角三角形(2)
一、教学目标:
知识目标:了解测量中的仰角、俯角等概念;会运用三角函数、直角三角形的知识解决与仰角、俯角有关的简单的实际问题。
能力目标:培养学生解决实际问题的能力,增强应用数学的意识。
情感目标:在自主学习、不断探索中享受成功的喜悦,体验学以致用的乐趣。
二、教学重点:
运用解直角三角形知识解决与仰角、俯角有关的实际问题
三、教学难点:
如何把实际问题转化为数学问题
四、学情分析:
本节课的主要内容是让学生学会建筑物等的测量,然后根据所得到的数据进行计算,从而知道所测物体的高度或长度,在教学中应该让学生对测量方法有一定的掌握。三边之间的关系a2+b2=c2(勾股定理);锐角之间的关系∠ A+ ∠ B= 90o边角之间的关系sinA=解直角三角形的依据(1)仰角和俯角铅垂线水平线视线视线仰角俯角(2)方向角如图:点A在O的北偏东30°
点B在点O的南偏西45°(西南方向) 运用解直角三角形知识解决与生活、生产有关的问题,主要涉及测量、航空、航海、工程等领域.
在测量时,须掌握仰角和俯角;方向角的概念.例 1解 在Rt△BDE中,
BE=DE×tan a
=AC×tan a
=22.7×tan 22°
≈9.17,
所以 AB=BE+AE
=BE+CD
=9.17+1.20
≈10.4(米).
答: 电线杆的高度约为10.4米.如图19.4.4,为了测量电线杆的高度AB,在离电线杆22.7米的C处,用高1.20米的测角仪CD测得电线杆顶端B的仰角a=22°,求电线杆AB的高.(精确到0.1米)30020米1.5米解: 在Rt⊿ABC中, ∠C=Rt∠, ∠BAC=300
∵ tanA=BC/AC
∴BC=AC·tanA=20·tan300=20×
而: CE=AF=1.5
∴ 旗杆高BE= (m)升国旗时,某同学站在离旗杆底部20米处行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角为30°,若双眼离地面1.5米,则旗杆高度为 米(用含根号的式子来表示).(一)试一试(二)你行吗?【例1】天空中有一个静止的广告气球C,从地面A点测得C的仰角为45°,从地面B点测得C点的仰角为60°,已知AB=20m,点C和直线AB在同一铅垂平面上,求气球离地面的高度?(结果保留根号)解:作CD⊥AB,垂足为D。设BD=x
在Rt⊿BCD中,CD=BD·tan∠CBD
=X·tan600=∵AD-BD=AB=20,即:∴气球离地面的高度为:在Rt⊿ACD中,AD=CD·cot∠DAC
= ·cot450=练一练1.如图所示,为了测量河对岸的旗杆AB的高度,在点C处测得旗杆顶端A的仰角为30°,沿CB方向前进5米到达D处,在D处测得旗杆顶端A的仰角为45°,
则旗杆AB的高度是 米。方法提炼:已知在RtΔABC中
∠ABC=90o,∠ACB=α,
∠ADB=β,AB=h,CD=a。
则:
在RtΔABC中,BC=AB?cotα
在RtΔADB中,DB=AB?cotβ
CB - DB=AB(cotα- cotβ)
所以:如图湖泊的中央有一个建筑物AB,某人在地面C处测得其顶部A的仰角为60o,然后自C处沿BC方向行100m至D处,又测得其顶部A的仰角为30o,求建筑物AB的高度。在山顶上处D有一铁塔,在塔顶B处测得地面上一点A的俯角α=60o,在塔底D测得点A的俯角β=45o,已知塔高BD=30米,求山高CD。ABCDαβ例 2(三)练一练 解:作BC⊥AM,垂足为C.
在Rt⊿ABC中,AB=28×1/2=14
∠BCA=900, ∠CAB=300
∴BC=AB·sin∠CAB
=14·sin300=14×1/2=7
∴ ∠1=600 ∠2=300在Rt⊿BCM中,BC=7 ∠CBM=∠2+150=450,
∴∠M=900- ∠CBM=450 ∴ CM=BC=7 答:船与灯塔的距离为:【例3】某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处,经16小时的航行到达,到达后必须立即卸货.此时,接到气象部门通知,一台风中心正以40海里/时的速度由A向北偏西60°方向移动,距台风中心200海里的圆形区域(包括边界)均会受到影响.
(1)问:B处是否会受到台风的影响?请说明理由.
(2)为避免受到台风的影响,该船应在多少小时内卸完货物?(供选用数据:(四)挑战自我【解析】(1)B处是否会受到台风的影响,只要求出点B
到AC的最短距离与台风中心半径相比较即可,故应过B
作BD⊥AC于 D.AB=20×16=320,∠CAB=30°?BD=160
<200 ∴B处受台风中心影响.(2)台风对B处若有影响,则B处到台风中心的距离不大
于200海里,则BE≤200,则DE=120,AD= 160 要在台风
到来之前卸完货物,必须在 2.如图所示,挂着“庆祝国庆”条幅的氢气球升在广场上空,已知气球的半径为2m,在地面A点测得气球中心O的仰角为60°,测得气球的视角
∠BAC=2°(B、C是⊙O上的点,
且OB⊥AB,OC⊥AC),则气球
中心O离地面的高度OD为( )
(sin 1°=0.0175,
结果精确到1m)
A.94m B.95m
C.99m D.105mC1.把实际问题转化成数学问题,这个转化为两个方面:一是将实际问题的图形转化为几何图形,画出正确的平面示意图,二是将已知条件转化为示意图中的边、角或它们之间的关系.2.把数学问题转化成解直角三角形问题,如果示意图不是
直角三角形,可添加适当的辅助线,画出直角三角形.方法小结:
