解比例或方程强化训练(专项突破)-小学数学六年级下册北师大版(含解析)
文档属性
| 名称 | 解比例或方程强化训练(专项突破)-小学数学六年级下册北师大版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-29 09:21:15 | ||
图片预览


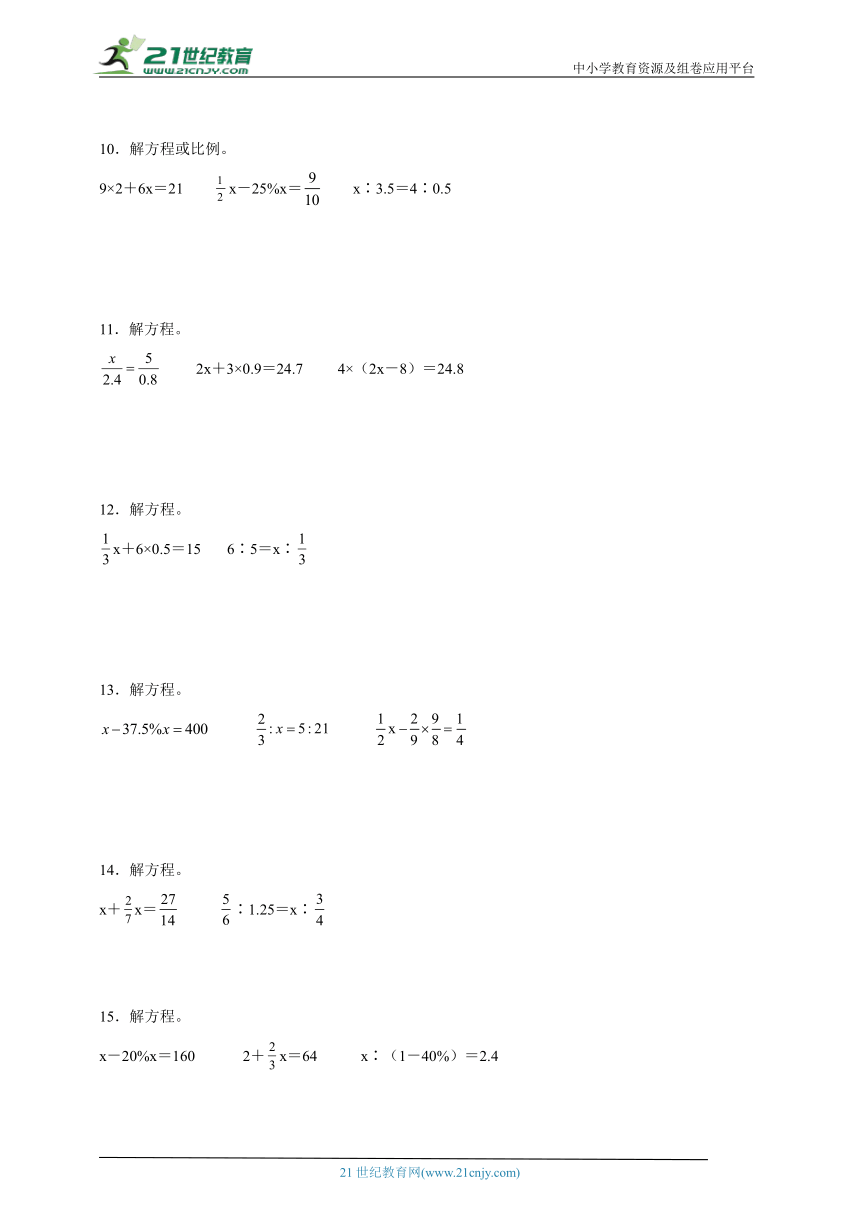


文档简介
中小学教育资源及组卷应用平台
解比例或方程强化训练(专项突破)-小学数学六年级下册北师大版
1.解方程。
21∶0.4=x∶ 1.6∶x=5∶0.5
2.解方程。
X+60%X=48
3.解方程或比例。
4.解方程。
(1)12∶x=18∶ (2)0.85x-50%x= (3)=
5.求未知数x:
x-0.8x=22 50%x-33%x=340
6∶0.5=x∶ =
6.求未知数x的值。
x+4.7=5 0.4x-0.4×4.5=10
7.解比例。
8.解方程。
9x-1.8=6.3 ∶=x∶
= 18:0.2=x∶
9.解比例。
∶=∶x (6+x)∶4=9∶5
= =
10.解方程或比例。
9×2+6x=21 x-25%x= x∶3.5=4∶0.5
11.解方程。
2x+3×0.9=24.7 4×(2x-8)=24.8
12.解方程。
x+6×0.5=15 6∶5=x∶
13.解方程。
14.解方程。
x+x= ∶1.25=x∶
15.解方程。
x-20%x=160 2+x=64 x∶(1-40%)=2.4
16.解方程。
(2.6+x)÷3=2.6
21%x+4=88
17.解方程。
x-60%x=36 40%x-= x∶7=6∶2.1
18.解方程。
=
19.解方程或比例。
20.解方程或比例。
x÷625%=2.6
参考答案:
1.x=17.5;x=15;x=0.16
【分析】根据比的基本性质,将原比例化成一般方程0.4x=21×,再根据等式的性质,方程两边都除以0.4即可;
根据比的基本性质,将原比例化成一般方程8x=24×5,再根据等式的性质,方程两边都除以8即可;
根据比的基本性质,将原比例化成一般方程5x=1.6×0.5,再根据等式的性质,方程两边都除以5即可。
【详解】21∶0.4=x∶
解:0.4x=21×
0.4x=7
0.4x÷0.4=7÷0.4
x=17.5
解:8x=24×5
8x=120
8x÷8=120÷8
x=15
1.6∶x=5∶0.5
解:5x=1.6×0.5
5x=0.8
5x÷5=0.8÷5
x=0.16
2.30;0.7;5.4
【分析】第一道算式先化简x+60%x,再运用等式的性质2两边同时除以1.6来求解;
第二道、第三道算式都可以运用比例的基本性质(在比例里,两个外项的积等于两个内项的积)认真计算,求出未知数的值。
【详解】X+60%X=48
解:(1+60%)x=48
1.6x÷1.6=48÷1.6
x=30
解:1×x=×0.8
x=0.7
解:0.8x=3.6×1.2
0.8x=4.32
0.8x÷0.8=4.32÷0.8
x=5.4
3.;;
;
【分析】根据等式的性质,方程两边同时减去18,再两边同时除以2求解;
根据比例的基本性质,原式化成,再根据等式的性质,方程两边同时除以0.7求解;
先化简方程,再根据等式的性质,方程两边同时加上求解;
先化简方程,再根据等式的性质,方程两边同时减去,再两边同时除以7.2求解。
【详解】
解:
解:
解:
解:
4.(1)x=;(2)x=;(3)x=2
【分析】(1)根据比例的基本性质转化为方程,运用等式的性质,方程两边同时除以18求解
(2)先计算方程的左边,根据等式的性质,方程两边同时除以0.35求解
(3)根据比例的基本性质转化为方程,运用等式的性质,方程两边同时除以30解
【详解】(1)12∶x=18∶
解:18x=12×
18x=50
18x÷18=50÷18
x=
(2)0.85x-50%x=
解:0.35x=
0.35x÷0.35=÷0.35
x=
(3)=
解:30x=12×5
30x=60
30x÷30=60÷30
x=2
5.x=110;x=2000
x=8;x=9.6
【分析】x-0.8x=22,先计算出1-0.8的差,再根据等式的性质2,方程两边同时除以1-0.8的差即可;
50%x-33%x=340,先计算50%-33%的差,再根据等式的性质2,方程两边同时除以50%-33%的差即可;
6∶0.5=x∶,解比例,原数化为:0.5x=6×,再根据等式的性质2,方程两边同时除以0.5即可;
=,解比例,原数化为:5x=12×4,再根据等式的性质2,方程两边同时除以5即可。
【详解】x-0.8x=22
解:0.2x=22
x=22÷0.2
x=110
50%x-33%x=340
解:17%x=340
x=340÷17%
x=2000
6∶0.5=x∶
解:0.5x=6×
0.5x=4
x=4÷0.5
x=8
=
解:5x=12×4
5x=48
x=48÷5
x=9.6
6.x=;x=;x=29.5
【分析】,根据比例的基本性质,先写成的形式,两边同时×即可;
x+4.7=5,根据等式的性质1和2,两边先同时-4.7,再同时×即可;
0.4x-0.4×4.5=10,根据等式的性质1和2,两边先同时+0.4×4.5的积,再同时÷0.4即可。
【详解】
解:
x+4.7=5
解:x+4.7-4.7=5-4.7
x=0.3
x×=×
x=
0.4x-0.4×4.5=10
解:0.4x-1.8+1.8=10+1.8
0.4x=11.8
0.4x÷0.4=11.8÷0.4
x=29.5
7.x=1.8;x=0.4;x=2
【分析】把比例转化为15x=45×60%,利用等式的基本性质方程的两边同时除以15求解;
把比例转化为75x=25×1.2,利用等式的基本性质方程的两边同时除以75求解;
把比例转化为x=×,利用等式的基本性质方程方程的两边同时除以求解;
【详解】
解:15x=45×60%
15x=27
15x÷15=27÷15
x=1.8
解:75x=25×1.2
75x=30
75x÷75=30÷75
x=0.4
解:x=×
x=1
x÷=1÷
x=2
8.X=0.9;X=;X=2;X=2.25
【分析】本题是求未知数x的题目。两种形式:一种形式是解方程,一种形式是解比例。解方程时依据等式的性质1和等式的性质2解答;解比例式时要根据比例的基本性质解答。
【详解】
9.x=;x=1.2
x=;x=
【分析】(1)根据比例的基本性质,两个外项的积等于两个内项的积,据此可得x=×,再根据等式的性质,把方程两边同时乘2即可解出比例;
(2)根据比例的基本性质,(6+x)×5=4×9,把方程两边同时除以5,再同时减去6即可解答;
(3)根据比例的基本性质可得120%x=40%×2,把方程两边同时除以120%即可;
(4)根据比例的基本性质,1.5x=3.2×4,把方程两边同时除以1.5即可解出比例。
【详解】∶=∶x
解:x=×
x=××2
x=
(6+x)∶4=9∶5
解:(6+x)×5=4×9
(6+x)×5=36
6+x=7.2
x=1.2
=
解:120%x=40%×2
1.2x=0.8
x=0.8÷1.2
x=
=
解:1.5x=3.2×4
1.5x=12.8
x=12.8÷1.5
x=
10.x=0.5;x=;x=28
【分析】9×2+6x=21,先计算出9×2的积,再根据等式的性质1,方程两边同时减去9×2的积,再根据等式的性质2,方程两边同时除以6,即可;
x-25%x=,先计算出-25%的差,再根据等式的性质2,方程两边同时除以-25%的差,即可;
x∶3.5=4∶0.5,解比例,原式化为:0.5x=3.5×4,再根据等式的性质2,方程两边同时除以0.5,即可。
【详解】9×2+6x=21
解:18+6x=21
6x=21-18
6x=3
x=3÷6
x=0.5
x-25%x=
解:x=
x=÷
x=×4
x=
x∶3.5=4∶0.5
解:0.5x=3.5×4
0.5x=14
x=14÷0.5
x=28
11.x=15;x=11;x=7.1
【分析】,解比例,原式化为:0.8x=2.4×5,再根据等式的性质2,方程两边同时除以0.8即可;
2x+3×0.9=24.7,先计算出3×0.9的积,再根据等式的性质1,方程两边同时减去3×0.9的积,再根据等式的性质2,方程两边同时除以2即可;
4×(2x-8)=24.8,根据等式的性质2,方程两边同时除以4,再根据等式的性质1,方程两边同时加上8,最后根据等式的性质2,方程两边同时除以2即可。
【详解】
解:0.8x=2.4×5
0.8x=12
x=12÷0.8
x=15
2x+3×0.9=24.7
解:2x+2.7=24.7
2x=24.7-2.7
2x=22
x=22÷2
x=11
4×(2x-8)=24.8
2x-8=24.8÷4
2x-8=6.2
2x=6.2+8
2x=14.2
x=14.2÷2
x=7.1
12.x=36;x=
【分析】先化简方程的左边,然后把方程的两边同时减去3,再同时除以即可;
先根据比例的性质,把比例方程转化成简易方程,再把方程两边同时除以5即可。
【详解】x+6×0.5=15
解:x+3=15
x+3-3=15-3
x=12
x÷=12÷
x=36
6∶5=x∶
解:5x=6×
5x=2
5x÷5=2÷5
x=
13.x=640;x=;x=1
【分析】合并方程左边同类项,再根据等式的性质2,方程的两边同时除以(1-37.5%)即可;
根据比例的基本性质将比例转化为方程:5x=×21,再根据等式的性质2,方程的两边同时除以5即可;
根据等式的性质1,方程的两边同时加上,再根据等式的性质2,方程的两边同时除以即可。
【详解】
解:(1-37.5%)x=400
x=400÷0.625
x=640
解:5x=×21
x=14÷5
x=
解:x=+
x=÷
x=1
14.x=;x=0.5
【分析】(1)先计算出方程左边x+x=x,再根据等式的性质,方程两边同时除以即可得到原方程的解;
(2)根据比例的性质,两外项之积等于两内项之积,把比例式转化成一般方程1.25x=×,再根据等式的性质,方程两边同时除以1.25即可得到原比例的解。
【详解】x+x=
解:x=
x÷=÷
x=
∶1.25=x∶
解:1.25x=×
1.25x÷1.25=×÷1.25
x=0.5
15.x=200;x=93;x=1.44
【分析】(1)先化简方程左边得80%x,再根据等式的性质,把方程两边同时除以80%即可解出方程;
(2)先把方程两边同时减去2,再同时乘即可解答;
(3)比的前项除以后项得出比值,据此用比值乘后项即可求出比的前项。
【详解】x-20%x=160
解:80%x=160
x=160÷0.8
x=200
2+x=64
解:x=62
x=62×
x=93
x∶(1-40%)=2.4
解:x=2.4×(1-40%)
x=2.4×0.6
x=1.44
16.x=2;x=5.2
x=400;x=32
【分析】根据比例的基本性质,原式化成7x=×35,再根据等式的性质,方程两边同时除以7求解;
根据等式的性质,方程两边同时乘上3,再两边同时减去2.6求解;
根据等式的性质,方程两边同时减去4,再两边同时除以21%求解;
先化简方程,再根据等式的性质,方程两边同时除以求解。
【详解】x∶ =35∶7
解:7x=×35
7x÷7=14÷7
x=2
(2.6+x)÷3=2.6
解:(2.6+x)÷3×3=2.6×3
2.6+x=7.8
2.6+x-2.6=7.8-2.6
x=5.2
21%x+4=88
解:21%x+4-4=88-4
21%x=84
21%x÷21%=84÷21%
x=400
3x-x=90
解:x=90
x÷=90÷
x=32
17.x=90;x=;x=20
【分析】解方程主要运用等式的性质,等式两边同时加上或者减去同一个数,等式不变。等式两边同时乘或者除以一个不为0的数,等式不变。把含有x的放在等号的一侧,不含x的放在等号的另一侧,然后把x前的系数除过去,就能得出x是多少;最后一个解比例,根据比例的基本性质:内项积=外项积,列出方程之后,再根据等式的性质解答即可;
【详解】x-60%x=36
解:40%x=36
x=36÷40%
x=90
40%x-=
解:40%x=+
40%x=
x=÷40%
x=
x∶7=6∶2.1
解:2.1x=6×7
2.1x=42
x=42÷2.1
x=20
18.x=1;x=;x=0.9375
【分析】=,解比例,原式化为:5×(x+2)=3×(x+4),化简,原式化为:5x+10
=3x+12,最后化为:2x=2,再用2÷2 ,即可解答;
,解比例,原式化为:5×(x-5)=21,化为:5x-25=21,再用21+25 的和除以5,即可解答;
,解比例,原式化为:4x=2.5×1.5,再用2.5×1.5的积除以4,即可解答。
【详解】=
解:5×(x+2)=3×(x+4)
5x+5×2=3x+3×4
5x-3x=12-10
2x=2
x=2÷2
x=1
解:5×(x-5)=3×7
5x-5×5=21
5x-25=21
5x=21+25
5x=46
x=46÷5
x=
解:4x=2.5×1.5
4x=3.75
x=3.75÷4
x=0.9375
19.=2;;
【分析】把百分数化成小数,计算方程左边的算式,方程两边同时除以1.7;把比例转化成乘积相等的形式,再方程两边同时除以 ;把比例转化成乘积相等的形式,然后方程两边同时除以8。
【详解】
解:1.7=3.4
=2
解:
解:
20.x=16.25;x=15.4;x=
【分析】x÷625%=2.6,用2.6×625%,即可解答;
2y-3.5×4=16.8,先计算出3.5×4的积,用16.8加上3.5×4的积,再除以2,即可解答;
∶35=x,解比例,原式化为:35×x=,再用除以35×的积,即可解答。
【详解】x÷625%=2.6
解:x=2.6×625%
x=16.25
2y-3.5×4=16.8
解:2y-14=16.8
2y=16.8+14
2y=30.8
y=30.8÷2
y=15.4
∶35=x
解:35×x=
40x=
x=÷40
x=×
x=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
解比例或方程强化训练(专项突破)-小学数学六年级下册北师大版
1.解方程。
21∶0.4=x∶ 1.6∶x=5∶0.5
2.解方程。
X+60%X=48
3.解方程或比例。
4.解方程。
(1)12∶x=18∶ (2)0.85x-50%x= (3)=
5.求未知数x:
x-0.8x=22 50%x-33%x=340
6∶0.5=x∶ =
6.求未知数x的值。
x+4.7=5 0.4x-0.4×4.5=10
7.解比例。
8.解方程。
9x-1.8=6.3 ∶=x∶
= 18:0.2=x∶
9.解比例。
∶=∶x (6+x)∶4=9∶5
= =
10.解方程或比例。
9×2+6x=21 x-25%x= x∶3.5=4∶0.5
11.解方程。
2x+3×0.9=24.7 4×(2x-8)=24.8
12.解方程。
x+6×0.5=15 6∶5=x∶
13.解方程。
14.解方程。
x+x= ∶1.25=x∶
15.解方程。
x-20%x=160 2+x=64 x∶(1-40%)=2.4
16.解方程。
(2.6+x)÷3=2.6
21%x+4=88
17.解方程。
x-60%x=36 40%x-= x∶7=6∶2.1
18.解方程。
=
19.解方程或比例。
20.解方程或比例。
x÷625%=2.6
参考答案:
1.x=17.5;x=15;x=0.16
【分析】根据比的基本性质,将原比例化成一般方程0.4x=21×,再根据等式的性质,方程两边都除以0.4即可;
根据比的基本性质,将原比例化成一般方程8x=24×5,再根据等式的性质,方程两边都除以8即可;
根据比的基本性质,将原比例化成一般方程5x=1.6×0.5,再根据等式的性质,方程两边都除以5即可。
【详解】21∶0.4=x∶
解:0.4x=21×
0.4x=7
0.4x÷0.4=7÷0.4
x=17.5
解:8x=24×5
8x=120
8x÷8=120÷8
x=15
1.6∶x=5∶0.5
解:5x=1.6×0.5
5x=0.8
5x÷5=0.8÷5
x=0.16
2.30;0.7;5.4
【分析】第一道算式先化简x+60%x,再运用等式的性质2两边同时除以1.6来求解;
第二道、第三道算式都可以运用比例的基本性质(在比例里,两个外项的积等于两个内项的积)认真计算,求出未知数的值。
【详解】X+60%X=48
解:(1+60%)x=48
1.6x÷1.6=48÷1.6
x=30
解:1×x=×0.8
x=0.7
解:0.8x=3.6×1.2
0.8x=4.32
0.8x÷0.8=4.32÷0.8
x=5.4
3.;;
;
【分析】根据等式的性质,方程两边同时减去18,再两边同时除以2求解;
根据比例的基本性质,原式化成,再根据等式的性质,方程两边同时除以0.7求解;
先化简方程,再根据等式的性质,方程两边同时加上求解;
先化简方程,再根据等式的性质,方程两边同时减去,再两边同时除以7.2求解。
【详解】
解:
解:
解:
解:
4.(1)x=;(2)x=;(3)x=2
【分析】(1)根据比例的基本性质转化为方程,运用等式的性质,方程两边同时除以18求解
(2)先计算方程的左边,根据等式的性质,方程两边同时除以0.35求解
(3)根据比例的基本性质转化为方程,运用等式的性质,方程两边同时除以30解
【详解】(1)12∶x=18∶
解:18x=12×
18x=50
18x÷18=50÷18
x=
(2)0.85x-50%x=
解:0.35x=
0.35x÷0.35=÷0.35
x=
(3)=
解:30x=12×5
30x=60
30x÷30=60÷30
x=2
5.x=110;x=2000
x=8;x=9.6
【分析】x-0.8x=22,先计算出1-0.8的差,再根据等式的性质2,方程两边同时除以1-0.8的差即可;
50%x-33%x=340,先计算50%-33%的差,再根据等式的性质2,方程两边同时除以50%-33%的差即可;
6∶0.5=x∶,解比例,原数化为:0.5x=6×,再根据等式的性质2,方程两边同时除以0.5即可;
=,解比例,原数化为:5x=12×4,再根据等式的性质2,方程两边同时除以5即可。
【详解】x-0.8x=22
解:0.2x=22
x=22÷0.2
x=110
50%x-33%x=340
解:17%x=340
x=340÷17%
x=2000
6∶0.5=x∶
解:0.5x=6×
0.5x=4
x=4÷0.5
x=8
=
解:5x=12×4
5x=48
x=48÷5
x=9.6
6.x=;x=;x=29.5
【分析】,根据比例的基本性质,先写成的形式,两边同时×即可;
x+4.7=5,根据等式的性质1和2,两边先同时-4.7,再同时×即可;
0.4x-0.4×4.5=10,根据等式的性质1和2,两边先同时+0.4×4.5的积,再同时÷0.4即可。
【详解】
解:
x+4.7=5
解:x+4.7-4.7=5-4.7
x=0.3
x×=×
x=
0.4x-0.4×4.5=10
解:0.4x-1.8+1.8=10+1.8
0.4x=11.8
0.4x÷0.4=11.8÷0.4
x=29.5
7.x=1.8;x=0.4;x=2
【分析】把比例转化为15x=45×60%,利用等式的基本性质方程的两边同时除以15求解;
把比例转化为75x=25×1.2,利用等式的基本性质方程的两边同时除以75求解;
把比例转化为x=×,利用等式的基本性质方程方程的两边同时除以求解;
【详解】
解:15x=45×60%
15x=27
15x÷15=27÷15
x=1.8
解:75x=25×1.2
75x=30
75x÷75=30÷75
x=0.4
解:x=×
x=1
x÷=1÷
x=2
8.X=0.9;X=;X=2;X=2.25
【分析】本题是求未知数x的题目。两种形式:一种形式是解方程,一种形式是解比例。解方程时依据等式的性质1和等式的性质2解答;解比例式时要根据比例的基本性质解答。
【详解】
9.x=;x=1.2
x=;x=
【分析】(1)根据比例的基本性质,两个外项的积等于两个内项的积,据此可得x=×,再根据等式的性质,把方程两边同时乘2即可解出比例;
(2)根据比例的基本性质,(6+x)×5=4×9,把方程两边同时除以5,再同时减去6即可解答;
(3)根据比例的基本性质可得120%x=40%×2,把方程两边同时除以120%即可;
(4)根据比例的基本性质,1.5x=3.2×4,把方程两边同时除以1.5即可解出比例。
【详解】∶=∶x
解:x=×
x=××2
x=
(6+x)∶4=9∶5
解:(6+x)×5=4×9
(6+x)×5=36
6+x=7.2
x=1.2
=
解:120%x=40%×2
1.2x=0.8
x=0.8÷1.2
x=
=
解:1.5x=3.2×4
1.5x=12.8
x=12.8÷1.5
x=
10.x=0.5;x=;x=28
【分析】9×2+6x=21,先计算出9×2的积,再根据等式的性质1,方程两边同时减去9×2的积,再根据等式的性质2,方程两边同时除以6,即可;
x-25%x=,先计算出-25%的差,再根据等式的性质2,方程两边同时除以-25%的差,即可;
x∶3.5=4∶0.5,解比例,原式化为:0.5x=3.5×4,再根据等式的性质2,方程两边同时除以0.5,即可。
【详解】9×2+6x=21
解:18+6x=21
6x=21-18
6x=3
x=3÷6
x=0.5
x-25%x=
解:x=
x=÷
x=×4
x=
x∶3.5=4∶0.5
解:0.5x=3.5×4
0.5x=14
x=14÷0.5
x=28
11.x=15;x=11;x=7.1
【分析】,解比例,原式化为:0.8x=2.4×5,再根据等式的性质2,方程两边同时除以0.8即可;
2x+3×0.9=24.7,先计算出3×0.9的积,再根据等式的性质1,方程两边同时减去3×0.9的积,再根据等式的性质2,方程两边同时除以2即可;
4×(2x-8)=24.8,根据等式的性质2,方程两边同时除以4,再根据等式的性质1,方程两边同时加上8,最后根据等式的性质2,方程两边同时除以2即可。
【详解】
解:0.8x=2.4×5
0.8x=12
x=12÷0.8
x=15
2x+3×0.9=24.7
解:2x+2.7=24.7
2x=24.7-2.7
2x=22
x=22÷2
x=11
4×(2x-8)=24.8
2x-8=24.8÷4
2x-8=6.2
2x=6.2+8
2x=14.2
x=14.2÷2
x=7.1
12.x=36;x=
【分析】先化简方程的左边,然后把方程的两边同时减去3,再同时除以即可;
先根据比例的性质,把比例方程转化成简易方程,再把方程两边同时除以5即可。
【详解】x+6×0.5=15
解:x+3=15
x+3-3=15-3
x=12
x÷=12÷
x=36
6∶5=x∶
解:5x=6×
5x=2
5x÷5=2÷5
x=
13.x=640;x=;x=1
【分析】合并方程左边同类项,再根据等式的性质2,方程的两边同时除以(1-37.5%)即可;
根据比例的基本性质将比例转化为方程:5x=×21,再根据等式的性质2,方程的两边同时除以5即可;
根据等式的性质1,方程的两边同时加上,再根据等式的性质2,方程的两边同时除以即可。
【详解】
解:(1-37.5%)x=400
x=400÷0.625
x=640
解:5x=×21
x=14÷5
x=
解:x=+
x=÷
x=1
14.x=;x=0.5
【分析】(1)先计算出方程左边x+x=x,再根据等式的性质,方程两边同时除以即可得到原方程的解;
(2)根据比例的性质,两外项之积等于两内项之积,把比例式转化成一般方程1.25x=×,再根据等式的性质,方程两边同时除以1.25即可得到原比例的解。
【详解】x+x=
解:x=
x÷=÷
x=
∶1.25=x∶
解:1.25x=×
1.25x÷1.25=×÷1.25
x=0.5
15.x=200;x=93;x=1.44
【分析】(1)先化简方程左边得80%x,再根据等式的性质,把方程两边同时除以80%即可解出方程;
(2)先把方程两边同时减去2,再同时乘即可解答;
(3)比的前项除以后项得出比值,据此用比值乘后项即可求出比的前项。
【详解】x-20%x=160
解:80%x=160
x=160÷0.8
x=200
2+x=64
解:x=62
x=62×
x=93
x∶(1-40%)=2.4
解:x=2.4×(1-40%)
x=2.4×0.6
x=1.44
16.x=2;x=5.2
x=400;x=32
【分析】根据比例的基本性质,原式化成7x=×35,再根据等式的性质,方程两边同时除以7求解;
根据等式的性质,方程两边同时乘上3,再两边同时减去2.6求解;
根据等式的性质,方程两边同时减去4,再两边同时除以21%求解;
先化简方程,再根据等式的性质,方程两边同时除以求解。
【详解】x∶ =35∶7
解:7x=×35
7x÷7=14÷7
x=2
(2.6+x)÷3=2.6
解:(2.6+x)÷3×3=2.6×3
2.6+x=7.8
2.6+x-2.6=7.8-2.6
x=5.2
21%x+4=88
解:21%x+4-4=88-4
21%x=84
21%x÷21%=84÷21%
x=400
3x-x=90
解:x=90
x÷=90÷
x=32
17.x=90;x=;x=20
【分析】解方程主要运用等式的性质,等式两边同时加上或者减去同一个数,等式不变。等式两边同时乘或者除以一个不为0的数,等式不变。把含有x的放在等号的一侧,不含x的放在等号的另一侧,然后把x前的系数除过去,就能得出x是多少;最后一个解比例,根据比例的基本性质:内项积=外项积,列出方程之后,再根据等式的性质解答即可;
【详解】x-60%x=36
解:40%x=36
x=36÷40%
x=90
40%x-=
解:40%x=+
40%x=
x=÷40%
x=
x∶7=6∶2.1
解:2.1x=6×7
2.1x=42
x=42÷2.1
x=20
18.x=1;x=;x=0.9375
【分析】=,解比例,原式化为:5×(x+2)=3×(x+4),化简,原式化为:5x+10
=3x+12,最后化为:2x=2,再用2÷2 ,即可解答;
,解比例,原式化为:5×(x-5)=21,化为:5x-25=21,再用21+25 的和除以5,即可解答;
,解比例,原式化为:4x=2.5×1.5,再用2.5×1.5的积除以4,即可解答。
【详解】=
解:5×(x+2)=3×(x+4)
5x+5×2=3x+3×4
5x-3x=12-10
2x=2
x=2÷2
x=1
解:5×(x-5)=3×7
5x-5×5=21
5x-25=21
5x=21+25
5x=46
x=46÷5
x=
解:4x=2.5×1.5
4x=3.75
x=3.75÷4
x=0.9375
19.=2;;
【分析】把百分数化成小数,计算方程左边的算式,方程两边同时除以1.7;把比例转化成乘积相等的形式,再方程两边同时除以 ;把比例转化成乘积相等的形式,然后方程两边同时除以8。
【详解】
解:1.7=3.4
=2
解:
解:
20.x=16.25;x=15.4;x=
【分析】x÷625%=2.6,用2.6×625%,即可解答;
2y-3.5×4=16.8,先计算出3.5×4的积,用16.8加上3.5×4的积,再除以2,即可解答;
∶35=x,解比例,原式化为:35×x=,再用除以35×的积,即可解答。
【详解】x÷625%=2.6
解:x=2.6×625%
x=16.25
2y-3.5×4=16.8
解:2y-14=16.8
2y=16.8+14
2y=30.8
y=30.8÷2
y=15.4
∶35=x
解:35×x=
40x=
x=÷40
x=×
x=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
