解直角三角形(四)[下学期]
图片预览

文档简介
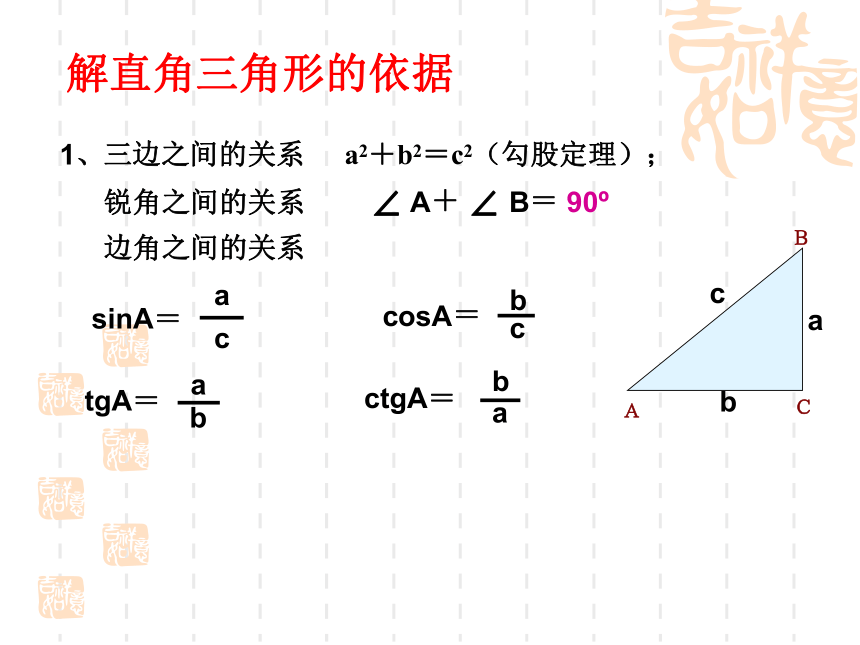
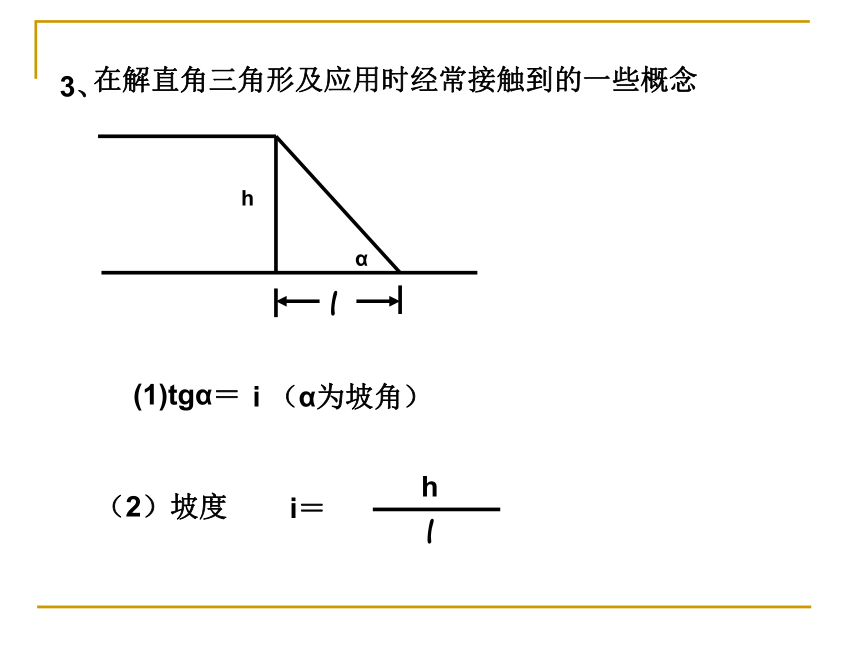
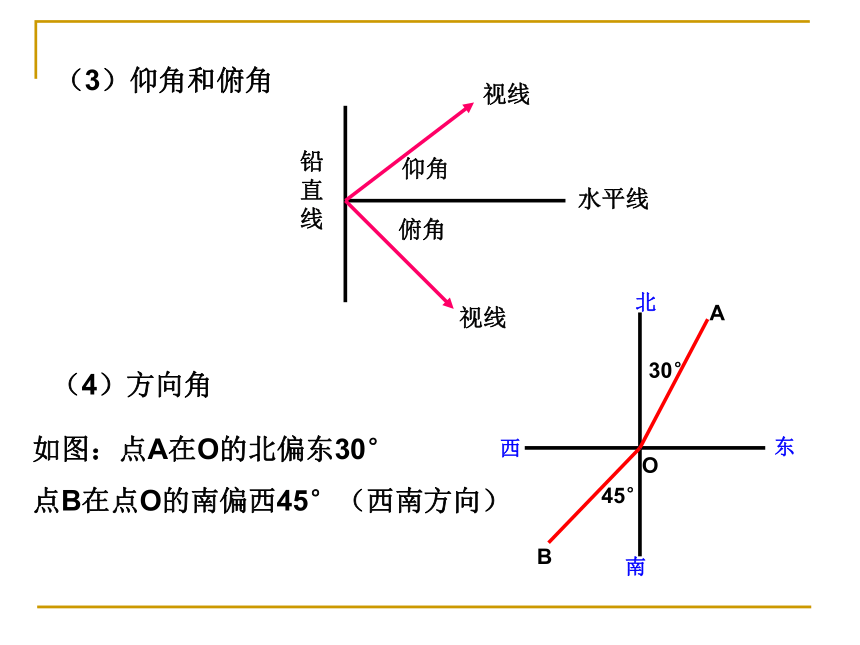
课件29张PPT。三边之间的关系a2+b2=c2(勾股定理);锐角之间的关系∠ A+ ∠ B= 90o边角之间的关系sinA=解直角三角形的依据1、3、在解直角三角形及应用时经常接触到的一些概念(3)仰角和俯角铅直线水平线视线视线仰角俯角(4)方向角如图:点A在O的北偏东30°
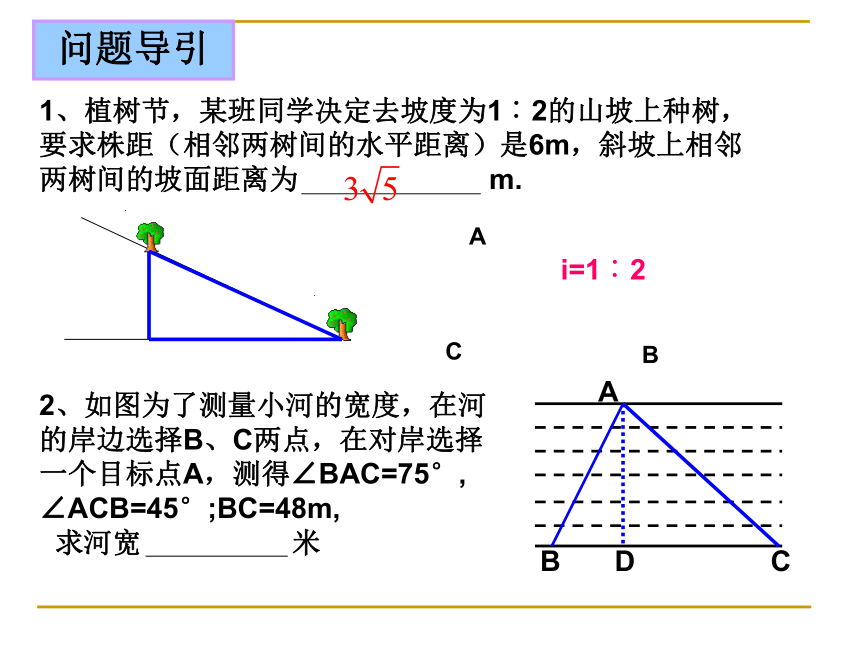
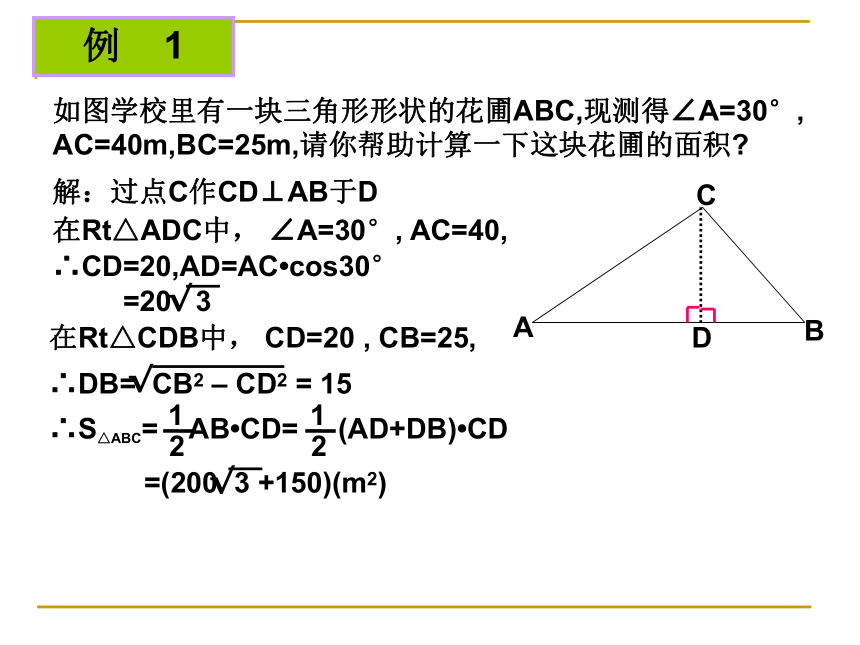
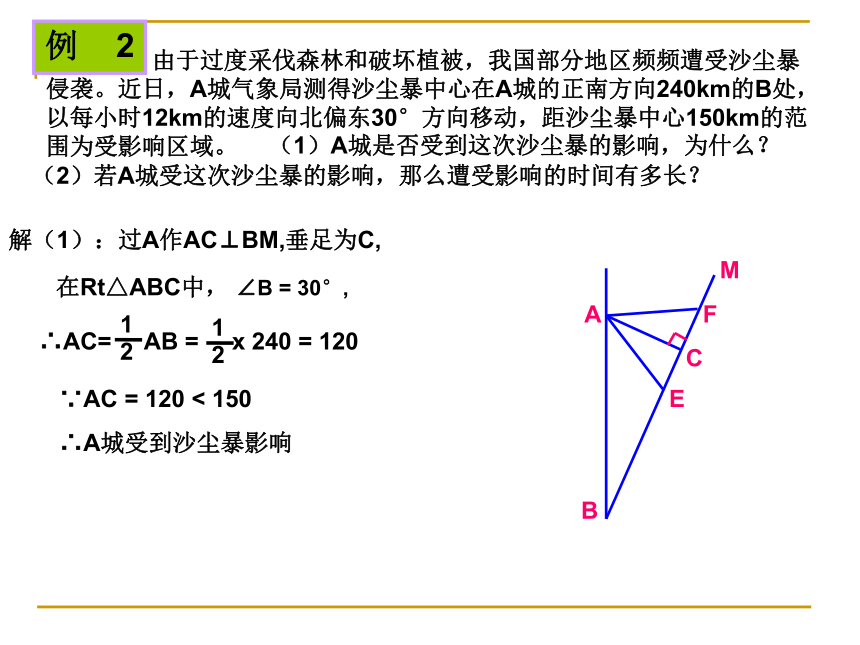
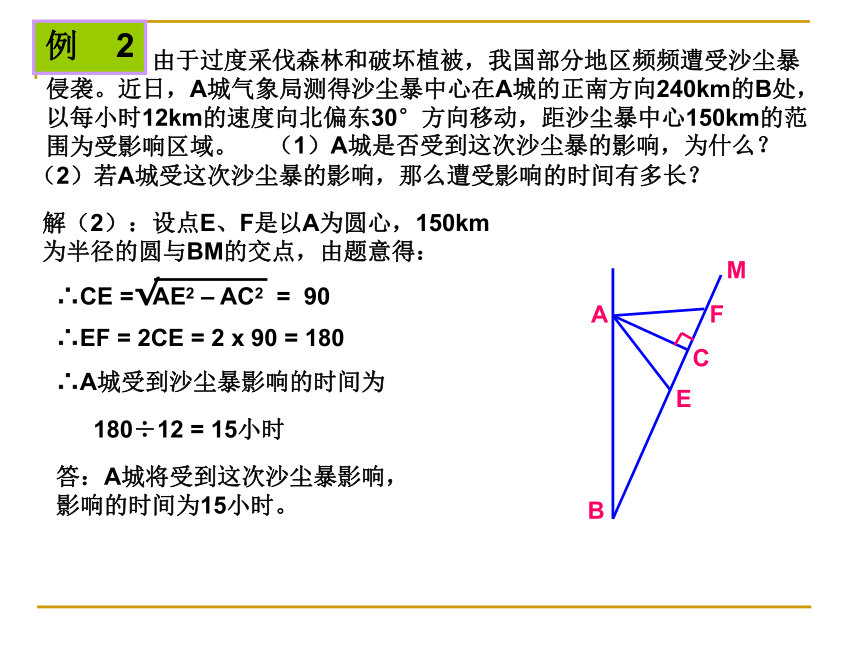
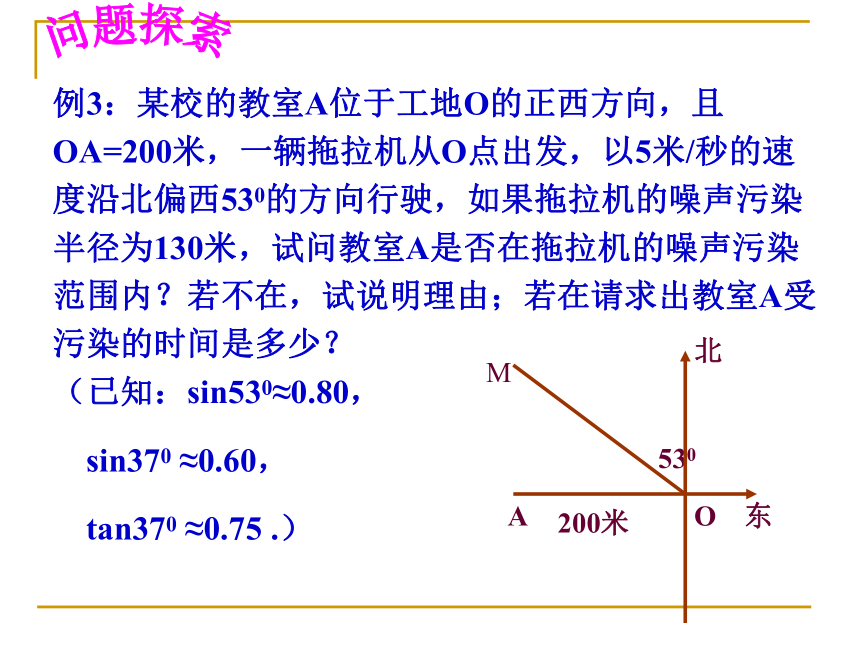
点B在点O的南偏西45°(西南方向)问题导引ACBi=1︰2D例 1如图学校里有一块三角形形状的花圃ABC,现测得∠A=30°, AC=40m,BC=25m,请你帮助计算一下这块花圃的面积?D解:过点C作CD⊥AB于D在Rt△ADC中, ∠A=30°, AC=40,∴CD=20,AD=AC?cos30°在Rt△CDB中, CD=20 , CB=25, 由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。例 2(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?解(1):过A作AC⊥BM,垂足为C,在Rt△ABC中, ∠B = 30°, ∵AC = 120 < 150∴A城受到沙尘暴影响 由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。例 2(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?解(2):设点E、F是以A为圆心,150km为半径的圆与BM的交点,由题意得:∴EF = 2CE = 2 x 90 = 180∴A城受到沙尘暴影响的时间为180÷12 = 15小时答:A城将受到这次沙尘暴影响,影响的时间为15小时。问题探索例3:某校的教室A位于工地O的正西方向,且OA=200米,一辆拖拉机从O点出发,以5米/秒的速度沿北偏西530的方向行驶,如果拖拉机的噪声污染半径为130米,试问教室A是否在拖拉机的噪声污染范围内?若不在,试说明理由;若在请求出教室A受污染的时间是多少? (已知:sin530≈0.80,
sin370 ≈0.60,
tan370 ≈0.75 .)
200米530问题探索解:作AB⊥OM于B , ∠AOB=900-530 = 370 在RtΔABO中 , ∵sin ∠AOB =
∴AB= AO·sin370 ≈ 200×0.60 =120 (米)∵120米<130米∴教室A在噪声污染范围内.在OM上取C、D两点,连结AC、AD,使 AC =AD = 130(米)∴CD =2BC =100(米)
∴100÷5 = 20(秒)答:教室受噪声污染的时间为20秒.B200米530CD三、例题讲解:例1、已知 中,∠C=Rt∠,sinA= , 求角A的
其它锐角三角函数值。 例2、在直角三角形ABC中,∠C=90o,∠A=60o两直角
边的 和为14,求这两条直角边的长。ABC图1例3一段河坝的横断面为等腰三角形ABCD,试根据下图中的数据求出坡角α和坝底宽AD。(单位是米,结果保留根号)ABCDEF46α3、在△ABC中,角A、B满足|tanA-1|+=0,则∠C= .4、已知α为锐角,tan(90°-α)=,则α的度数为( )
(A)30° (B)45°
(C)60° (D)75°5、如果是锐角,且,那么的值是( ).
(A)(B) (C)(D) 22、如图,点A是一个半径为300米的圆形
森林公园的中心,在森林公园附近有B、C
两个村庄,现要在B、C两村庄之间修一条
长为1000米的笔直公路将两村连通.经测得
∠ABC=45°,∠ACB =30°,问此公路是
否会穿过该森林公园?请通过计算进行说明.某校的教室A位于工地O的正西方向,且
OA=200米,一辆拖拉机从O点出发,以
5米/秒的速度沿北偏西530的方向行驶,
如果拖拉机的噪声污染半径为130米,试
问教室A是否在拖拉机的噪声污染范围内?若不在,试说明理由;若在请求出教室A受污染的时间是多少?
(已知:sin530≈0.80,sin370 ≈0.60,
tan370 ≈0.75 .)1、 我军某部在一次野外训练中,有一辆坦克准备通过一座
小山,已知山脚和山顶的水平距离为1000米,山高为565米,
如果这辆坦克能够爬300 的斜坡,试问:它能不能通过这座
小山?〖达标练习〗1、本节例题学习以后,我们可以得到解直角三角形的两种基本图形:小结:2、注意可解直角三角形与非可解直角三角形的基本解题思路;3、 现实对象 数学模型 实际问题的解 数学问题的解 数学抽象 逻辑推理 翻译回去 有无解? 练习1 在下列直角三角形中,不能求出解的水( )
A 已知一直角边和所对的角 B 已知两个锐角
C 已知斜边和一个锐角 D 已知两直角边
2 在Rt△ABC中,∠C=900,cosB=2/3,则 a:b:c=( )
A 2:√5:3 B 1:√2:√3 C 2:√5:√3 D 1:2:3
3 在Rt△ ABC中,CD为斜边AB上的高,则下列线段的比等于sinA的是( )
A AB/BC B CD/AC C BD/DC D BC/AC
4 在△ ABC中,C =900,A=600,两直角边的和为14,则a=( )
A 21-7√3 B 7√3-7 C 14√3 D 1+√3
5 在△ ABC中,∠B=450,∠C=600,BC边上的高AD=3,则BC=( )
A 3+3√3 B 2+√3 C 3+√3 D √2+√6
6 在等腰△ ABC中,顶角为锐角,一腰上的高线为1 ,这条高线与
另一腰的夹角为450,则三角形ABC的面积为( )
A √2/2 B √3 C 1/2 D 1/4选择1 在Rt△ABC中, ∠C=900,如果已知b和∠A,则a= , c= (用锐角三角函数表示)
2 在△ ABC中,C =900,A=600,a+b=3+√3,则c
山坡与地面成300的倾斜角,某人上坡走60米,则他上升 米,
坡度是
如图已知堤坝的横断面为梯形,AD坡面的水平宽度为3√3米,
DC=4米,B=600,则(1)斜坡AD 的铅直高度是
(2)斜坡AD 的长是 (3)坡角A的度数是
(4)堤坝底AB的长是 (5)斜坡BC的长是
5 如图从山 顶A望地面的C、D 两点,俯角分别时450、600,测得 CD=100米,设山高AB=x则列出关于X的方程是 解得x= i=1:√3填空(第4题)(第5题)解答题:
1.在Rt△ABC中, ∠C=900,a+b=12, tgB=2,求C的值及∠ABD的度数.
2.山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角β==600,在塔底C处测得A的α=450,已知塔高为60米,求山高.
3.通过一座小山,已知 山脚和山顶的水平距离为1550米,山高为565米,如果这辆坦克能够爬250的斜坡,试问:它能部能通过这座小山 ?
4 外国船只,除特许外,不得进入我国海洋100海里以内的区域,如图,设A、B是我们的观察站,A和B 之间的距离为157.73海里,海岸线是过A、B的一条直线,一外国船只在P点,在A点测得∠BAP=450,同时在B点测得∠ABP=600,问此时是否要向外国船只发出警告,令其退出我国海域.αβ备用题:
1 在Rt△ ABC中,CD为斜边AB上的高,则下列线段的比等于sinA的是( )
A AB/BC B CD/AC C BD/DC D BC/AC
2 在△ ABC中,C =900,A=600,两直角边的和为14,则a=( )
A 21-7√3 B 7√3-7 C 14√3 D 1+√3
3 在△ ABC中,∠B=450,∠C=600,BC边上的高AD=3,则BC=( )
A 3+3√3 B 2+√3 C 3+√3 D √2+√6
4 山坡与地面成300的倾斜角,某人上坡走60米,则他上升 米,坡度是
5 如图从山 顶A望地面的C、D 两点,俯角分别时450、600,测得CD=100米
设山高AB=x,则列出关于X的方程是 解得x=
6 湖 面上有一塔,其高为h在塔上测得空中一气球的仰角α ,又测得气球在湖中的俯角为β,
试求气球距湖面的高度h.
7 我军某部在一次野外训练中,有一辆坦克准备通过一座小山,已知山脚和山顶的 水平
距离为1550米,山高为565米,如果这辆坦克能够爬250的斜坡,试问:它能部能通过这座小?ABCD特殊三角形30?,45?,105?;45?,60?,75?;30?,15?,135 ? ;45?,15?,120?.推广: ?ABC中,tgC=0.5, sinB=0.9, AC=4, BC=6,求BC.例 1 在?ABC中,?B=45?,AB=3,?C=60 ? ,求BC及?ABC的面积。
练习:?ABC,?B=45 ? ,?C=15?,BC=10,求BC及AC。D例 2 已知:四边形ABCD中,AB=2.8, ?B=45?, BC=6.7,CD=3.4。
求四边形ABCD的面积。 EF再 见
点B在点O的南偏西45°(西南方向)问题导引ACBi=1︰2D例 1如图学校里有一块三角形形状的花圃ABC,现测得∠A=30°, AC=40m,BC=25m,请你帮助计算一下这块花圃的面积?D解:过点C作CD⊥AB于D在Rt△ADC中, ∠A=30°, AC=40,∴CD=20,AD=AC?cos30°在Rt△CDB中, CD=20 , CB=25, 由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。例 2(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?解(1):过A作AC⊥BM,垂足为C,在Rt△ABC中, ∠B = 30°, ∵AC = 120 < 150∴A城受到沙尘暴影响 由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。例 2(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?解(2):设点E、F是以A为圆心,150km为半径的圆与BM的交点,由题意得:∴EF = 2CE = 2 x 90 = 180∴A城受到沙尘暴影响的时间为180÷12 = 15小时答:A城将受到这次沙尘暴影响,影响的时间为15小时。问题探索例3:某校的教室A位于工地O的正西方向,且OA=200米,一辆拖拉机从O点出发,以5米/秒的速度沿北偏西530的方向行驶,如果拖拉机的噪声污染半径为130米,试问教室A是否在拖拉机的噪声污染范围内?若不在,试说明理由;若在请求出教室A受污染的时间是多少? (已知:sin530≈0.80,
sin370 ≈0.60,
tan370 ≈0.75 .)
200米530问题探索解:作AB⊥OM于B , ∠AOB=900-530 = 370 在RtΔABO中 , ∵sin ∠AOB =
∴AB= AO·sin370 ≈ 200×0.60 =120 (米)∵120米<130米∴教室A在噪声污染范围内.在OM上取C、D两点,连结AC、AD,使 AC =AD = 130(米)∴CD =2BC =100(米)
∴100÷5 = 20(秒)答:教室受噪声污染的时间为20秒.B200米530CD三、例题讲解:例1、已知 中,∠C=Rt∠,sinA= , 求角A的
其它锐角三角函数值。 例2、在直角三角形ABC中,∠C=90o,∠A=60o两直角
边的 和为14,求这两条直角边的长。ABC图1例3一段河坝的横断面为等腰三角形ABCD,试根据下图中的数据求出坡角α和坝底宽AD。(单位是米,结果保留根号)ABCDEF46α3、在△ABC中,角A、B满足|tanA-1|+=0,则∠C= .4、已知α为锐角,tan(90°-α)=,则α的度数为( )
(A)30° (B)45°
(C)60° (D)75°5、如果是锐角,且,那么的值是( ).
(A)(B) (C)(D) 22、如图,点A是一个半径为300米的圆形
森林公园的中心,在森林公园附近有B、C
两个村庄,现要在B、C两村庄之间修一条
长为1000米的笔直公路将两村连通.经测得
∠ABC=45°,∠ACB =30°,问此公路是
否会穿过该森林公园?请通过计算进行说明.某校的教室A位于工地O的正西方向,且
OA=200米,一辆拖拉机从O点出发,以
5米/秒的速度沿北偏西530的方向行驶,
如果拖拉机的噪声污染半径为130米,试
问教室A是否在拖拉机的噪声污染范围内?若不在,试说明理由;若在请求出教室A受污染的时间是多少?
(已知:sin530≈0.80,sin370 ≈0.60,
tan370 ≈0.75 .)1、 我军某部在一次野外训练中,有一辆坦克准备通过一座
小山,已知山脚和山顶的水平距离为1000米,山高为565米,
如果这辆坦克能够爬300 的斜坡,试问:它能不能通过这座
小山?〖达标练习〗1、本节例题学习以后,我们可以得到解直角三角形的两种基本图形:小结:2、注意可解直角三角形与非可解直角三角形的基本解题思路;3、 现实对象 数学模型 实际问题的解 数学问题的解 数学抽象 逻辑推理 翻译回去 有无解? 练习1 在下列直角三角形中,不能求出解的水( )
A 已知一直角边和所对的角 B 已知两个锐角
C 已知斜边和一个锐角 D 已知两直角边
2 在Rt△ABC中,∠C=900,cosB=2/3,则 a:b:c=( )
A 2:√5:3 B 1:√2:√3 C 2:√5:√3 D 1:2:3
3 在Rt△ ABC中,CD为斜边AB上的高,则下列线段的比等于sinA的是( )
A AB/BC B CD/AC C BD/DC D BC/AC
4 在△ ABC中,C =900,A=600,两直角边的和为14,则a=( )
A 21-7√3 B 7√3-7 C 14√3 D 1+√3
5 在△ ABC中,∠B=450,∠C=600,BC边上的高AD=3,则BC=( )
A 3+3√3 B 2+√3 C 3+√3 D √2+√6
6 在等腰△ ABC中,顶角为锐角,一腰上的高线为1 ,这条高线与
另一腰的夹角为450,则三角形ABC的面积为( )
A √2/2 B √3 C 1/2 D 1/4选择1 在Rt△ABC中, ∠C=900,如果已知b和∠A,则a= , c= (用锐角三角函数表示)
2 在△ ABC中,C =900,A=600,a+b=3+√3,则c
山坡与地面成300的倾斜角,某人上坡走60米,则他上升 米,
坡度是
如图已知堤坝的横断面为梯形,AD坡面的水平宽度为3√3米,
DC=4米,B=600,则(1)斜坡AD 的铅直高度是
(2)斜坡AD 的长是 (3)坡角A的度数是
(4)堤坝底AB的长是 (5)斜坡BC的长是
5 如图从山 顶A望地面的C、D 两点,俯角分别时450、600,测得 CD=100米,设山高AB=x则列出关于X的方程是 解得x= i=1:√3填空(第4题)(第5题)解答题:
1.在Rt△ABC中, ∠C=900,a+b=12, tgB=2,求C的值及∠ABD的度数.
2.山顶上有一座电视塔,在塔顶B处测得地面上一点A的俯角β==600,在塔底C处测得A的α=450,已知塔高为60米,求山高.
3.通过一座小山,已知 山脚和山顶的水平距离为1550米,山高为565米,如果这辆坦克能够爬250的斜坡,试问:它能部能通过这座小山 ?
4 外国船只,除特许外,不得进入我国海洋100海里以内的区域,如图,设A、B是我们的观察站,A和B 之间的距离为157.73海里,海岸线是过A、B的一条直线,一外国船只在P点,在A点测得∠BAP=450,同时在B点测得∠ABP=600,问此时是否要向外国船只发出警告,令其退出我国海域.αβ备用题:
1 在Rt△ ABC中,CD为斜边AB上的高,则下列线段的比等于sinA的是( )
A AB/BC B CD/AC C BD/DC D BC/AC
2 在△ ABC中,C =900,A=600,两直角边的和为14,则a=( )
A 21-7√3 B 7√3-7 C 14√3 D 1+√3
3 在△ ABC中,∠B=450,∠C=600,BC边上的高AD=3,则BC=( )
A 3+3√3 B 2+√3 C 3+√3 D √2+√6
4 山坡与地面成300的倾斜角,某人上坡走60米,则他上升 米,坡度是
5 如图从山 顶A望地面的C、D 两点,俯角分别时450、600,测得CD=100米
设山高AB=x,则列出关于X的方程是 解得x=
6 湖 面上有一塔,其高为h在塔上测得空中一气球的仰角α ,又测得气球在湖中的俯角为β,
试求气球距湖面的高度h.
7 我军某部在一次野外训练中,有一辆坦克准备通过一座小山,已知山脚和山顶的 水平
距离为1550米,山高为565米,如果这辆坦克能够爬250的斜坡,试问:它能部能通过这座小?ABCD特殊三角形30?,45?,105?;45?,60?,75?;30?,15?,135 ? ;45?,15?,120?.推广: ?ABC中,tgC=0.5, sinB=0.9, AC=4, BC=6,求BC.例 1 在?ABC中,?B=45?,AB=3,?C=60 ? ,求BC及?ABC的面积。
练习:?ABC,?B=45 ? ,?C=15?,BC=10,求BC及AC。D例 2 已知:四边形ABCD中,AB=2.8, ?B=45?, BC=6.7,CD=3.4。
求四边形ABCD的面积。 EF再 见
