解直角三角形复习课[下学期]
图片预览



文档简介
课件22张PPT。第19章 解直角三角形
(复习课) 学习目标1,明确本章的知识结构。2,回顾勾股定理的证明(拼图方法),进一步理解勾
股定理。3,进一步理解三角函数的意义,熟悉特殊角的三角函
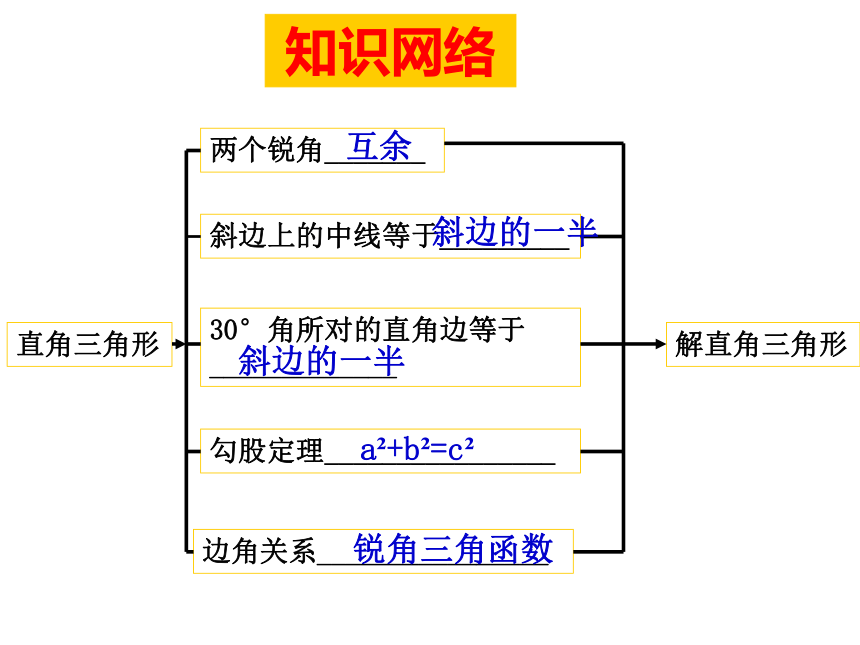
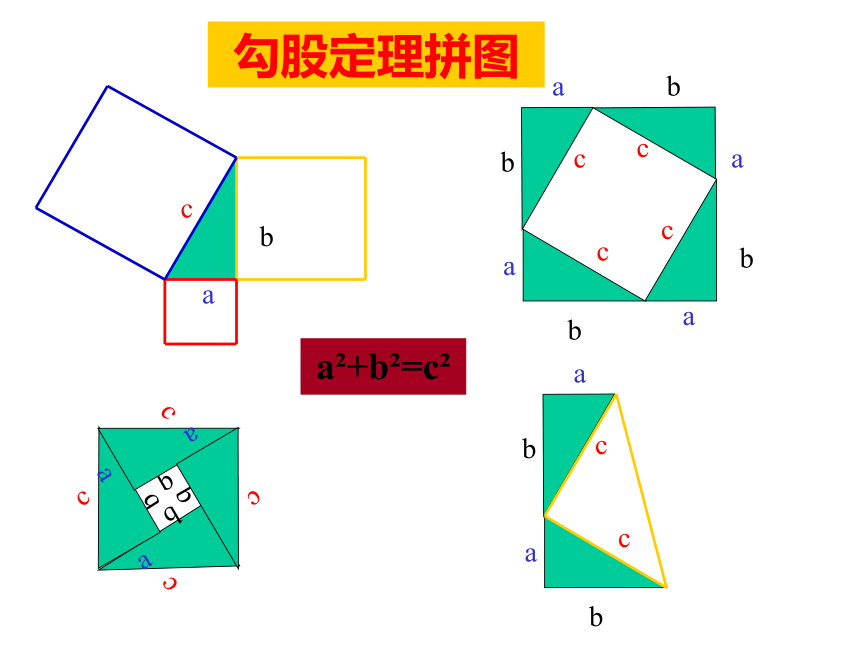
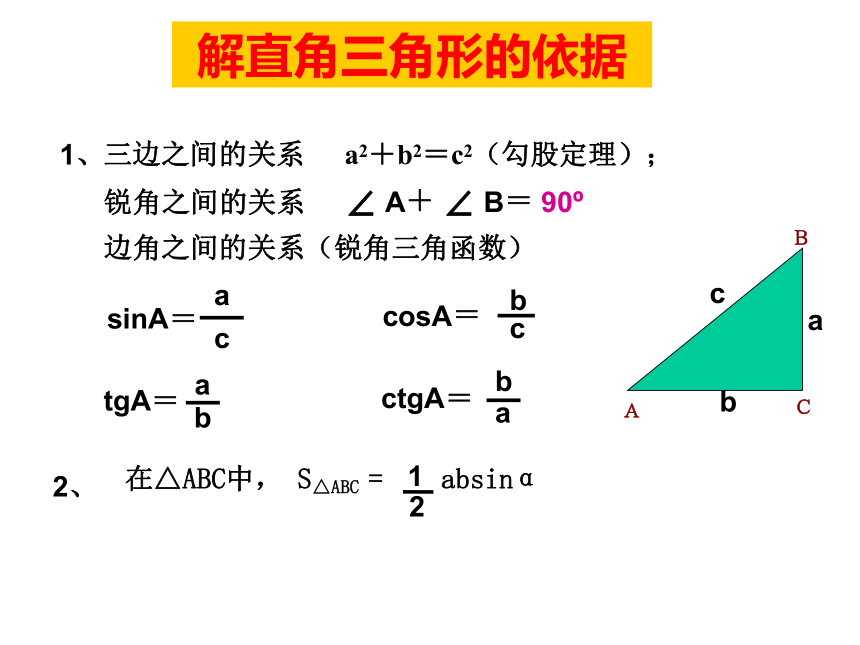
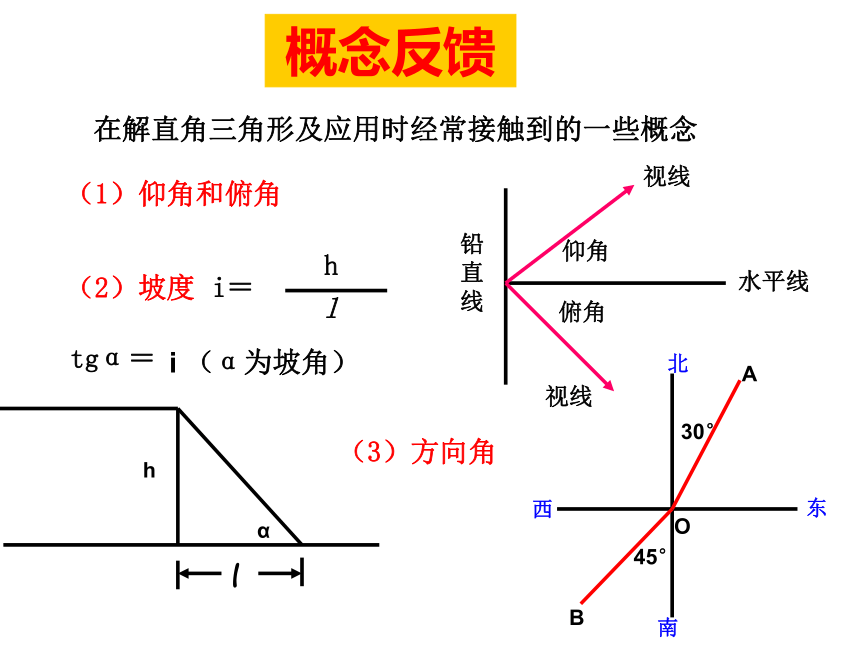
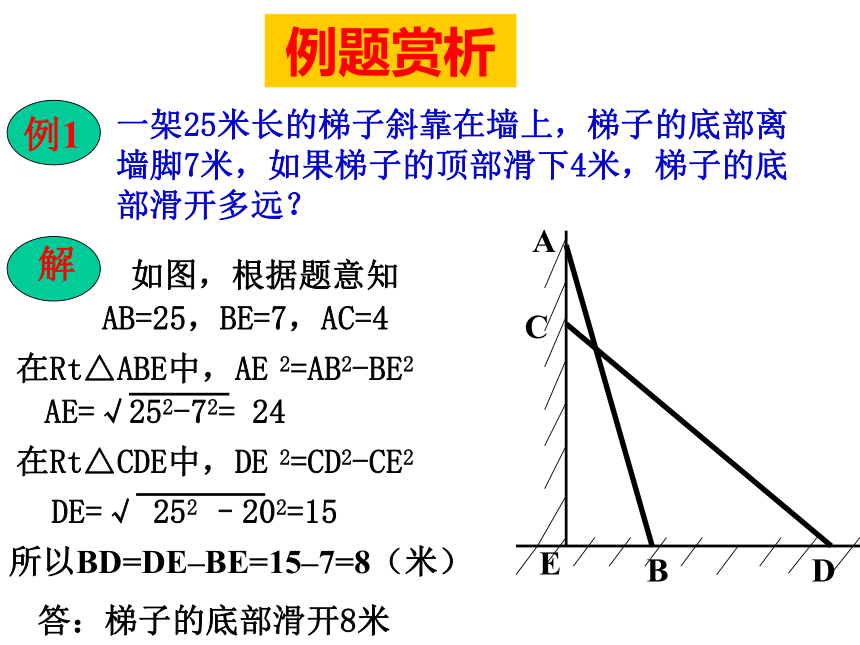
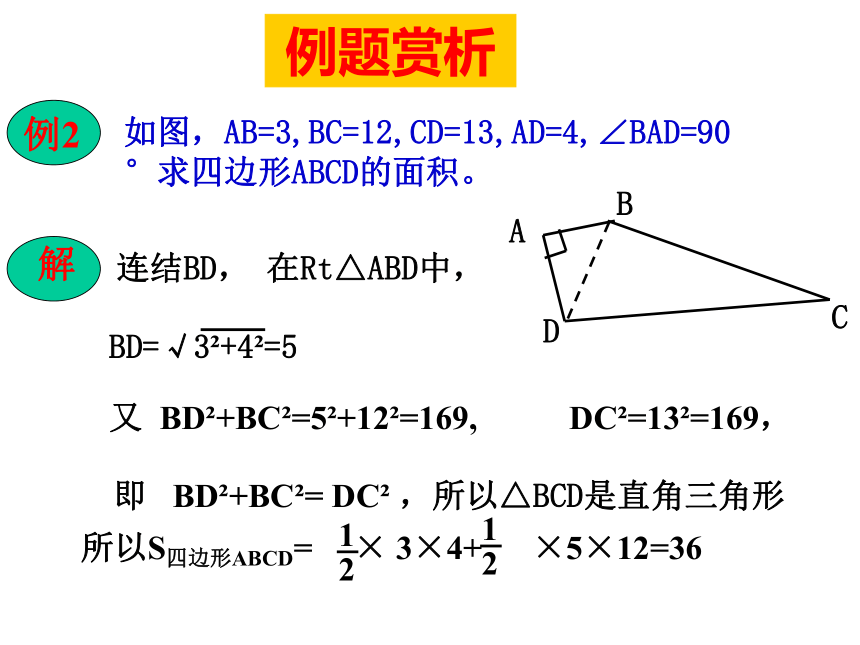
数值。4,进一步掌握直角三角形的解法。5,学会运用勾股定理和三角函数解决实际问题。知识网络两个锐角_______斜边上的中线等于_________30°角所对的直角边等于_____________直角三角形勾股定理________________边角关系________________解直角三角形互余斜边的一半斜边的一半a2+b2=c2锐角三角函数勾股定理拼图a2+b2=c2三边之间的关系a2+b2=c2(勾股定理);锐角之间的关系∠ A+ ∠ B= 90o边角之间的关系(锐角三角函数)sinA=1、解直角三角形的依据在解直角三角形及应用时经常接触到的一些概念概念反馈(1)仰角和俯角(3)方向角例题赏析一架25米长的梯子斜靠在墙上,梯子的底部离墙脚7米,如果梯子的顶部滑下4米,梯子的底部滑开多远?如图,根据题意知AB=25,BE=7,AC=4在Rt△ABE中,AE 2=AB2-BE2在Rt△CDE中,DE 2=CD2-CE2所以BD=DE–BE=15–7=8(米)答:梯子的底部滑开8米例题赏析如图,AB=3,BC=12,CD=13,AD=4,∠BAD=90 °求四边形ABCD的面积。在Rt△ABD中,连结BD,又 BD2+BC2=52+122=169, DC2=132=169,即 BD2+BC2= DC2 ,所以△BCD是直角三角形当堂训练一1,以下列数据为三角形的边长,则不能构成直角三角形的一组是( )A,3,4,5, B,5,12,13,
C,6 ,8 ,10 D,7,8,93,如果直角三角形的两条直角边之和为7,斜边长为5,则三角形的面积是 。2,如果直角三角形的两条边长为3厘米、4厘米,则其周长是 。4,如图,有一张藏宝图,根据图中的数据,起点A与宝藏B的直线距离是( )A,9 B,10
C,11 D, 12AB4226121D6B当堂训练一5,如图,图中直角三角形的两条直角边的长分别是6和8,则图中半圆R的面积是( )PRQA,10 Л B,25 Л
C,12.5 Л D,100 Л6, 池塘里一枝荷花高出水面20厘米,一阵劲风吹来,荷花从根部向一边倾斜,顶端与水面平齐,如图,已知荷花被风吹动的水平距离是60厘米,求池塘中水的深度。(80厘米)C巩固练习一1,课本第119页复习题第1、2、3题。例题赏析(2)如果tanA·cot60°=1,A=_________。(3)已知cosα<0.5,那么锐角α的取值范围是( ) A, 60°<α<90° B, 0°< α <60° C,30°< α <90° D, 0°< α <30°(4)如果√cosA – — + | √3 tanB –3|=012那么△ABC是( ) A,直角三角形 B,锐角三角形
C,钝角三角形 D,等边三角形。260° AD2例题赏析如图学校里有一块三角形形状的花圃ABC,现测得∠A=30°, AC=40m,BC=25m,请你帮助计算一下这块花圃的面积?过点C作CD⊥AB于D在Rt△ADC中, ∠A=30°, AC=40,∴CD=20, AD=AC?cos30°在Rt△CDB中, CD=20 , CB=25,例题赏析如图,在△ ABC中,AD是BC边上的高,若tanB=cos∠DAC,(1)AC与BD相等吗?说明理由;故 BD=AC(1)例题赏析如图,在△ ABC中,AD是BC边上的高,若tanB=cos∠DAC,(1)AC与BD相等吗?说明理由;(2)设AC=13k,AD=12k,所以CD=5k,又AC=BD=13k,例题赏析如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60?方向,航行24海里到C处,见岛A在北偏西30?方向,货轮继续向西航行,有无触礁的危险?过点A作AD⊥BC于D,设AD=x∵ ∠NBA= 60?, ∠N1BA= 30?,∴ ∠ABC=30?, ∠ACD= 60?,在Rt△ADC中, CD=AD?ctg∠ACD= x?ctg60?, 在Rt△ADB中, BD=AD?ctg30?= x?ctg30?, ∵ BD-CD=BC,BC=24 ∴ x?ctg30?- x?ctg60?=24 答:货轮无触礁危险。当堂训练二1,在Rt△ABC中,如果各边都扩大2倍,则锐角A的正
弦值和余弦值( )A,都不变 B,都扩大2倍 C,都缩小2倍 D,不确定。4,如果α和β都是锐角,且sinα= cosβ,
则α与β的关系 是( )A,相等 B,互余 C,互补 D,不确定。A75°BA当堂训练二当堂训练二解(2):设点E、F是以A为圆心,150km为半径的圆与BM的交点,由题意得:∴EF = 2CE = 2 x 90 = 180∴A城受到沙尘暴影响的时间为180÷12 = 15小时答:A城将受到这次沙尘暴影响,影响的时间为15小时。3,由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?EF3,由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?当堂训练二解(1):过A作AC⊥BM,垂足为C,在Rt△ABC中, ∠B = 30°, ∵AC = 120 < 150∴A城受到沙尘暴影响学习小结一,知识小结: 本节课主要复习勾股定理、锐角三角函数、勾股定理在解题中的应用,三角函数在解三角形中的应用。二,方法归纳; 在涉及四边形问题时,经常把四边形进行适当分割,划分为三角形和特殊四边形,再借助特殊四边形的特征和直角三角形知识解决问题。巩固练习一1,如图,在△ABC中, ∠C=90°,点D在BC上,
BD=4,AD=BC,求:(1)DC的长;(2)sinB的值2 ,课本第119——121页第4、7、9、10、11、13、14题。3,选作:课本第121页第15、16、17题。
(复习课) 学习目标1,明确本章的知识结构。2,回顾勾股定理的证明(拼图方法),进一步理解勾
股定理。3,进一步理解三角函数的意义,熟悉特殊角的三角函
数值。4,进一步掌握直角三角形的解法。5,学会运用勾股定理和三角函数解决实际问题。知识网络两个锐角_______斜边上的中线等于_________30°角所对的直角边等于_____________直角三角形勾股定理________________边角关系________________解直角三角形互余斜边的一半斜边的一半a2+b2=c2锐角三角函数勾股定理拼图a2+b2=c2三边之间的关系a2+b2=c2(勾股定理);锐角之间的关系∠ A+ ∠ B= 90o边角之间的关系(锐角三角函数)sinA=1、解直角三角形的依据在解直角三角形及应用时经常接触到的一些概念概念反馈(1)仰角和俯角(3)方向角例题赏析一架25米长的梯子斜靠在墙上,梯子的底部离墙脚7米,如果梯子的顶部滑下4米,梯子的底部滑开多远?如图,根据题意知AB=25,BE=7,AC=4在Rt△ABE中,AE 2=AB2-BE2在Rt△CDE中,DE 2=CD2-CE2所以BD=DE–BE=15–7=8(米)答:梯子的底部滑开8米例题赏析如图,AB=3,BC=12,CD=13,AD=4,∠BAD=90 °求四边形ABCD的面积。在Rt△ABD中,连结BD,又 BD2+BC2=52+122=169, DC2=132=169,即 BD2+BC2= DC2 ,所以△BCD是直角三角形当堂训练一1,以下列数据为三角形的边长,则不能构成直角三角形的一组是( )A,3,4,5, B,5,12,13,
C,6 ,8 ,10 D,7,8,93,如果直角三角形的两条直角边之和为7,斜边长为5,则三角形的面积是 。2,如果直角三角形的两条边长为3厘米、4厘米,则其周长是 。4,如图,有一张藏宝图,根据图中的数据,起点A与宝藏B的直线距离是( )A,9 B,10
C,11 D, 12AB4226121D6B当堂训练一5,如图,图中直角三角形的两条直角边的长分别是6和8,则图中半圆R的面积是( )PRQA,10 Л B,25 Л
C,12.5 Л D,100 Л6, 池塘里一枝荷花高出水面20厘米,一阵劲风吹来,荷花从根部向一边倾斜,顶端与水面平齐,如图,已知荷花被风吹动的水平距离是60厘米,求池塘中水的深度。(80厘米)C巩固练习一1,课本第119页复习题第1、2、3题。例题赏析(2)如果tanA·cot60°=1,A=_________。(3)已知cosα<0.5,那么锐角α的取值范围是( ) A, 60°<α<90° B, 0°< α <60° C,30°< α <90° D, 0°< α <30°(4)如果√cosA – — + | √3 tanB –3|=012那么△ABC是( ) A,直角三角形 B,锐角三角形
C,钝角三角形 D,等边三角形。260° AD2例题赏析如图学校里有一块三角形形状的花圃ABC,现测得∠A=30°, AC=40m,BC=25m,请你帮助计算一下这块花圃的面积?过点C作CD⊥AB于D在Rt△ADC中, ∠A=30°, AC=40,∴CD=20, AD=AC?cos30°在Rt△CDB中, CD=20 , CB=25,例题赏析如图,在△ ABC中,AD是BC边上的高,若tanB=cos∠DAC,(1)AC与BD相等吗?说明理由;故 BD=AC(1)例题赏析如图,在△ ABC中,AD是BC边上的高,若tanB=cos∠DAC,(1)AC与BD相等吗?说明理由;(2)设AC=13k,AD=12k,所以CD=5k,又AC=BD=13k,例题赏析如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60?方向,航行24海里到C处,见岛A在北偏西30?方向,货轮继续向西航行,有无触礁的危险?过点A作AD⊥BC于D,设AD=x∵ ∠NBA= 60?, ∠N1BA= 30?,∴ ∠ABC=30?, ∠ACD= 60?,在Rt△ADC中, CD=AD?ctg∠ACD= x?ctg60?, 在Rt△ADB中, BD=AD?ctg30?= x?ctg30?, ∵ BD-CD=BC,BC=24 ∴ x?ctg30?- x?ctg60?=24 答:货轮无触礁危险。当堂训练二1,在Rt△ABC中,如果各边都扩大2倍,则锐角A的正
弦值和余弦值( )A,都不变 B,都扩大2倍 C,都缩小2倍 D,不确定。4,如果α和β都是锐角,且sinα= cosβ,
则α与β的关系 是( )A,相等 B,互余 C,互补 D,不确定。A75°BA当堂训练二当堂训练二解(2):设点E、F是以A为圆心,150km为半径的圆与BM的交点,由题意得:∴EF = 2CE = 2 x 90 = 180∴A城受到沙尘暴影响的时间为180÷12 = 15小时答:A城将受到这次沙尘暴影响,影响的时间为15小时。3,由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?EF3,由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴侵袭。近日,A城气象局测得沙尘暴中心在A城的正南方向240km的B处,以每小时12km的速度向北偏东30°方向移动,距沙尘暴中心150km的范围为受影响区域。(1)A城是否受到这次沙尘暴的影响,为什么?(2)若A城受这次沙尘暴的影响,那么遭受影响的时间有多长?当堂训练二解(1):过A作AC⊥BM,垂足为C,在Rt△ABC中, ∠B = 30°, ∵AC = 120 < 150∴A城受到沙尘暴影响学习小结一,知识小结: 本节课主要复习勾股定理、锐角三角函数、勾股定理在解题中的应用,三角函数在解三角形中的应用。二,方法归纳; 在涉及四边形问题时,经常把四边形进行适当分割,划分为三角形和特殊四边形,再借助特殊四边形的特征和直角三角形知识解决问题。巩固练习一1,如图,在△ABC中, ∠C=90°,点D在BC上,
BD=4,AD=BC,求:(1)DC的长;(2)sinB的值2 ,课本第119——121页第4、7、9、10、11、13、14题。3,选作:课本第121页第15、16、17题。
