【大单元教学】鲁教版2023年六年级大单元大教研 第五章基本平面图形 第七章 相交线与平行线 课件(24张PPT)
文档属性
| 名称 | 【大单元教学】鲁教版2023年六年级大单元大教研 第五章基本平面图形 第七章 相交线与平行线 课件(24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 989.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 09:03:10 | ||
图片预览







文档简介
(共24张PPT)
第五章 基本平面图形
单元教学
鲁教版六年级数学下册
整体结构
本章主要内容有几何图形,直线、射线、线段,角的度量,角的比较与运算,多边形和圆的初步认识。教材从生活中常见的立体与平面图形入手,通过实例,在丰富的现实情境中,使学生经历对几何体的研究的数学活动过程,通过实例,在丰富的现实情境中,使学生经历对简单的平面图形直线、射线、线段与角的研究的数学活动过程,通过动手画图、线段的大小比较及角的度量、比较与运算等活动过程,理解并掌握这些图形的一些简单性质。
教学目标
(1)经历画图等数学活动过程,掌握直线和角的一些简单性质;掌握直线、射线、线段和角的表示方法;掌握角的度量方法.
(2)在现实情境中,探索两条线段、两个角的比较方法及比较的结果,探索线段与线段之间、角与角之间的数量关系.
(3)认识线段的等分点,角的平分线.
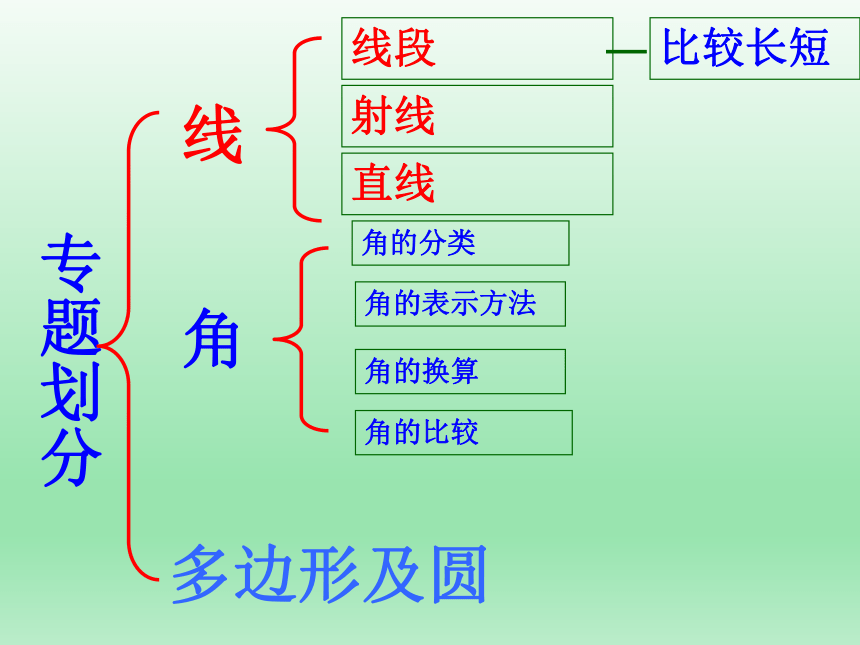
专题划分
角
线
线段
射线
直线
角的分类
角的换算
角的表示方法
比较长短
多边形及圆
角的比较
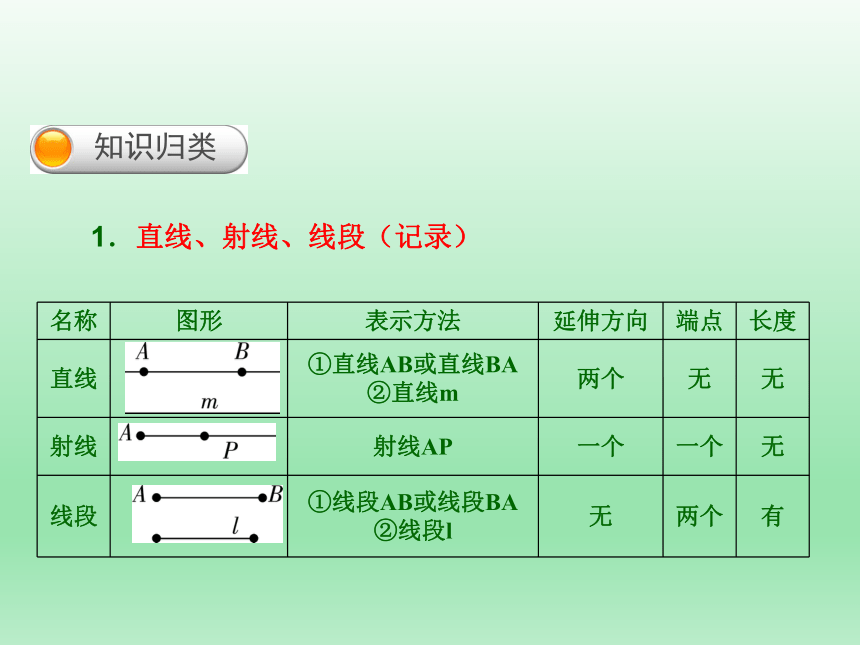
知识归类
1.直线、射线、线段(记录)
名称 图形 表示方法 延伸方向 端点 长度
直线 ①直线AB或直线BA
②直线m 两个 无 无
射线 射线AP 一个 一个 无
线段 ①线段AB或线段BA
②线段l 无 两个 有
2.直线的基本性质
经过两点有且只有____条直线.
3.线段的基本性质
两点之间,____________最短.
4.两点之间的距离(记录)
两点之间线段的________,叫做这两点之间的距离.距离是指线段的_______,是一个_______,而不是指线段本身.
5.比较两条线段长短的方法
(1)叠合法:把它们放在同一条_______上比较;
一
线段
长度
长度
数值
直线
(2)度量法:用刻度尺量出两条线段的长度进行比较.
6.线段的中点
若点M把线段AB分成_______的两条线段AM、BM,则点M叫做线段AB的中点.这时有AM=______=____ ,AB=_______=1/2 ________.(记录)
相等
BM
AB
2AM
2BM
数学·新课标(BS)
7.角
(1)概念:角由两条具有公共_______的射线组成,两条射线的公共______是这个角的________,这两条射线叫做角的____;从动态观点看,角是一条射线绕_______从起始位置旋转到终止位置所组成的图形.
(2)表示方法:①三个大写英文字母表示,中间的字母表示_______,其他两个字母分别表示两条边上的任意一点;②用一个数字或小写________字母表示;③用一个大写_______字母表示,前提是以这个点为顶点的角只有一个.
端点
端点
顶点
边
端点
顶点
希腊
英文
(3)单位及换算:把周角平均分成360份,每一份就是1°的角,1°的1/60就是1′,1′的1/60就是1″,即1°= ____,1′=________.(记录)
(4)分类:小于平角的角可按大小分成三类:当一个角等于平角的一半时,这个角叫做________;大于0°角小于直角的角叫做________;大于直角而小于平角的角叫做__________.
8.角的平分线
从一个角的_______引出的一条射线,把这个角分成两个_________的角,这条射线叫做这个角的平分线.
60′
60′
直角
锐角
钝角
顶点
相等
角的度量(记录)
钟表角度(★)
方位角(画一下)
与角平分线有关求角度
多边形(记录)
多边形的顶点、边、内角、对角 线、分割的三角形
圆心角与扇形面积
多边形(记录)
多边形的顶点、边、内角、对角线、分割的三角形
圆心角与扇形面积
…
思考: n边形共有 条对角线
多边形 四边形 五边形 六边形 … n边形
过点A对角线条数
分成三角形个数
A
1
2
3
2
3
4
n-3
n-2
引申为一元二次方程的应用(握手问题)
尺规作图(记录)
如何作线段的和、差
第七章相交线与平行线
整体结构
平面内两条直线的位置关系是“空间与图形”所要研究的基本问题,本章是在学生已有知识和经验的基础上,对平面内两条直线的位置关系的进一步探索。本章首先研究了相交的情形,探究了两直线相交所成的角的位置和大小关系,给出了邻补角和对顶角概念,得出了“对顶角相等”的结论;垂直作为两条直线相交的特殊情形,与 它有关的概念和结论是学习下一章“平面直角坐标系”的直接基础,本章对垂直的情形进行了专门的研究,探索得出了“过一点有且只有一条直线与已知直线垂直”“垂线段最短”等结论,并给出点到直线的距离的概念,为学面直角坐标系中确定点的坐标打下基础.命题是以后研究形式逻辑概念和术语的基础。
教学目标
学会相交线、平行线的相关知识及平移的知识,并运用它们解释、解决问题
经历相交线和平行线的应用过程,提高学生的数学应用意识;
丰富对现实空间及图形的认识,建立初步的空间观察,发展形象思维;
经历观察、实验、猜想、证明等数学活动过程,发展合情推理能力和初步的演绎推理能力,能用语言有条理地阐述自己的观点;
学会与他人合作,并能与他人交流思想的过程和结果;
初步形成评价与反思的意识.
空间想象能力:从让学生观察图形人手,逐步培养识图、抽象、概括能力
教学内容
本单元的教学内容为相交线与平行线及其在现实生活中的应用,平面内两条直线的位置关系是“空间与图形”所要研究的基本问题,这些内容学生在前两个学段已经有所接触,本章在学生已有知识和经验的基础上,继续研究平面内两条直线的位置关系,是学生开始接触几何逻辑推导的初步。主要研究平面内两条直线的位置关系,重点是垂直和平行关系,以及有关平移变换的内容,难点是运用逻辑思维解决几何问题,以及对集合语言的组织与运用。
专题划分
专题一:首先研究相交的情形:探究了两直线相交所成的角的位置和大小关系,给出了领补角和对顶角概念;垂直作为两条直线相交的特殊情形,是学习下一章“平面直角坐标系”的直接基础,本章对垂直的情形进行了专门的研究,探索得出了“同一平面内,过一点有且只有一条直线与已知直线垂直”“垂线段最短”等结论,并给出点到直线的距离的概念。
专题二:平行线的判定公理、判定定理、平行线的性质:理解判定定理的形成、判定定理的证法,学会运用平行线的性质,了解表达推理证明的方式,同位角、内错角、同旁内角的概念。让学生知道公理与定理的区别,体验从实践中总结知识,从逻辑推导中扩展知识的过程。
专题三:认识图形的平移、应用及相关概念,学会利用平行线段以及对应点画出平移图形,知道平移的几个要点,知道一些平移的应用。
相交线
两条
直线
相交
两条直线被
第三条所截
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
特殊
垂直
平面内,过一点有且只有一条
直线与已知直线垂直
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
平行线
平行公理及其推论
探索直线平行线的条件
平行线的性质
过直线外一点有且只有一条直线
与这条直线平行
平行于同一条直线的两条直线平行
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
概念
同位角:在截线同旁,被截线相同的一侧的两角.
内错角:在截线两旁,被截线之内的两角
同旁内角:在截线同旁,被截线之内的两角
同位角的边构成“F“形,内错角的边构成”Z“形,同旁内角的边构成”U“形.
判断直线平行的条件
图形
已知
结果
理由
同位角
内错角
同旁内角
a//b
a//b
a//b
同位角相等
两直线平行
内错角相等
两直线平行
同旁内角互补
两直线平行
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
平行线的判定
图形
已知
结果
理由
同位角
内错角
同旁内角
a//b
a//b
内错角相等
两直线平行
同旁内角互补
两直线平行
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
平行线的性质
a//b
同位角相等
两直线平行
a//b
同位角相等
两直线平行
a//b
同位角相等
两直线平行
a//b
两直线平行
同位角相等
同旁内角互补
a//b
两直线平行
平行线的性质
∠2=∠3
a//b
同位角相等
两直线平行
a//b
两直线平行
内错角相等
平行线的性质
条 件
结论
两直线平 行
同位角相 等
内错角相等
同旁内角互补
平行线的判定
同位角相等
内错角相等
同旁内角互补
两直线平行
线的关系
角的关系
角的关系
线的关系
判定
性质
平行线的性质和平行线的判定方法的
区 别 与 联 系
两直线平行
{
1.同位角相等
2.内错角相等
3.同旁内角互补
性质
判定
1.由_________得到___________的结论是平行线的判定;
请注意:
2.由____________得到______________的结论是平行线的性质.
用途:
用途:
角的关系
两直线平行
说明直线平行
两直线平行
角相等或互补
说明角相等或互补
已知: ∠AOB。
“作一个角等于已知角”
B
O
A
求作: ∠A’O’B’ 使∠A’O’B’=∠AOB。
O’
A’
(2) 以点O为圆心,
任意长为半径
交OA于点C,
(3) 以点O’为圆心,
画弧,
C
D
同样(OD)长为半径
画弧,
C’
(4) 以点C’为圆心,
CD长为半径
画弧,
D’
(5) 过点D’作射线O’B’.
B’
A’
O’
B’
∠A’O’B’就是所求的角.
作 法 示 范
(1) 作射线O’A’;
交OB于点D;
交O’A’于点C’;
交前面的弧于点D’ ,
作法演示
第五章 基本平面图形
单元教学
鲁教版六年级数学下册
整体结构
本章主要内容有几何图形,直线、射线、线段,角的度量,角的比较与运算,多边形和圆的初步认识。教材从生活中常见的立体与平面图形入手,通过实例,在丰富的现实情境中,使学生经历对几何体的研究的数学活动过程,通过实例,在丰富的现实情境中,使学生经历对简单的平面图形直线、射线、线段与角的研究的数学活动过程,通过动手画图、线段的大小比较及角的度量、比较与运算等活动过程,理解并掌握这些图形的一些简单性质。
教学目标
(1)经历画图等数学活动过程,掌握直线和角的一些简单性质;掌握直线、射线、线段和角的表示方法;掌握角的度量方法.
(2)在现实情境中,探索两条线段、两个角的比较方法及比较的结果,探索线段与线段之间、角与角之间的数量关系.
(3)认识线段的等分点,角的平分线.
专题划分
角
线
线段
射线
直线
角的分类
角的换算
角的表示方法
比较长短
多边形及圆
角的比较
知识归类
1.直线、射线、线段(记录)
名称 图形 表示方法 延伸方向 端点 长度
直线 ①直线AB或直线BA
②直线m 两个 无 无
射线 射线AP 一个 一个 无
线段 ①线段AB或线段BA
②线段l 无 两个 有
2.直线的基本性质
经过两点有且只有____条直线.
3.线段的基本性质
两点之间,____________最短.
4.两点之间的距离(记录)
两点之间线段的________,叫做这两点之间的距离.距离是指线段的_______,是一个_______,而不是指线段本身.
5.比较两条线段长短的方法
(1)叠合法:把它们放在同一条_______上比较;
一
线段
长度
长度
数值
直线
(2)度量法:用刻度尺量出两条线段的长度进行比较.
6.线段的中点
若点M把线段AB分成_______的两条线段AM、BM,则点M叫做线段AB的中点.这时有AM=______=____ ,AB=_______=1/2 ________.(记录)
相等
BM
AB
2AM
2BM
数学·新课标(BS)
7.角
(1)概念:角由两条具有公共_______的射线组成,两条射线的公共______是这个角的________,这两条射线叫做角的____;从动态观点看,角是一条射线绕_______从起始位置旋转到终止位置所组成的图形.
(2)表示方法:①三个大写英文字母表示,中间的字母表示_______,其他两个字母分别表示两条边上的任意一点;②用一个数字或小写________字母表示;③用一个大写_______字母表示,前提是以这个点为顶点的角只有一个.
端点
端点
顶点
边
端点
顶点
希腊
英文
(3)单位及换算:把周角平均分成360份,每一份就是1°的角,1°的1/60就是1′,1′的1/60就是1″,即1°= ____,1′=________.(记录)
(4)分类:小于平角的角可按大小分成三类:当一个角等于平角的一半时,这个角叫做________;大于0°角小于直角的角叫做________;大于直角而小于平角的角叫做__________.
8.角的平分线
从一个角的_______引出的一条射线,把这个角分成两个_________的角,这条射线叫做这个角的平分线.
60′
60′
直角
锐角
钝角
顶点
相等
角的度量(记录)
钟表角度(★)
方位角(画一下)
与角平分线有关求角度
多边形(记录)
多边形的顶点、边、内角、对角 线、分割的三角形
圆心角与扇形面积
多边形(记录)
多边形的顶点、边、内角、对角线、分割的三角形
圆心角与扇形面积
…
思考: n边形共有 条对角线
多边形 四边形 五边形 六边形 … n边形
过点A对角线条数
分成三角形个数
A
1
2
3
2
3
4
n-3
n-2
引申为一元二次方程的应用(握手问题)
尺规作图(记录)
如何作线段的和、差
第七章相交线与平行线
整体结构
平面内两条直线的位置关系是“空间与图形”所要研究的基本问题,本章是在学生已有知识和经验的基础上,对平面内两条直线的位置关系的进一步探索。本章首先研究了相交的情形,探究了两直线相交所成的角的位置和大小关系,给出了邻补角和对顶角概念,得出了“对顶角相等”的结论;垂直作为两条直线相交的特殊情形,与 它有关的概念和结论是学习下一章“平面直角坐标系”的直接基础,本章对垂直的情形进行了专门的研究,探索得出了“过一点有且只有一条直线与已知直线垂直”“垂线段最短”等结论,并给出点到直线的距离的概念,为学面直角坐标系中确定点的坐标打下基础.命题是以后研究形式逻辑概念和术语的基础。
教学目标
学会相交线、平行线的相关知识及平移的知识,并运用它们解释、解决问题
经历相交线和平行线的应用过程,提高学生的数学应用意识;
丰富对现实空间及图形的认识,建立初步的空间观察,发展形象思维;
经历观察、实验、猜想、证明等数学活动过程,发展合情推理能力和初步的演绎推理能力,能用语言有条理地阐述自己的观点;
学会与他人合作,并能与他人交流思想的过程和结果;
初步形成评价与反思的意识.
空间想象能力:从让学生观察图形人手,逐步培养识图、抽象、概括能力
教学内容
本单元的教学内容为相交线与平行线及其在现实生活中的应用,平面内两条直线的位置关系是“空间与图形”所要研究的基本问题,这些内容学生在前两个学段已经有所接触,本章在学生已有知识和经验的基础上,继续研究平面内两条直线的位置关系,是学生开始接触几何逻辑推导的初步。主要研究平面内两条直线的位置关系,重点是垂直和平行关系,以及有关平移变换的内容,难点是运用逻辑思维解决几何问题,以及对集合语言的组织与运用。
专题划分
专题一:首先研究相交的情形:探究了两直线相交所成的角的位置和大小关系,给出了领补角和对顶角概念;垂直作为两条直线相交的特殊情形,是学习下一章“平面直角坐标系”的直接基础,本章对垂直的情形进行了专门的研究,探索得出了“同一平面内,过一点有且只有一条直线与已知直线垂直”“垂线段最短”等结论,并给出点到直线的距离的概念。
专题二:平行线的判定公理、判定定理、平行线的性质:理解判定定理的形成、判定定理的证法,学会运用平行线的性质,了解表达推理证明的方式,同位角、内错角、同旁内角的概念。让学生知道公理与定理的区别,体验从实践中总结知识,从逻辑推导中扩展知识的过程。
专题三:认识图形的平移、应用及相关概念,学会利用平行线段以及对应点画出平移图形,知道平移的几个要点,知道一些平移的应用。
相交线
两条
直线
相交
两条直线被
第三条所截
一般情况
邻补角
对顶角
邻补角互补
对顶角相等
特殊
垂直
平面内,过一点有且只有一条
直线与已知直线垂直
垂线段最短
点到直线的距离
同位角、内错角、同旁内角
平行线
平行公理及其推论
探索直线平行线的条件
平行线的性质
过直线外一点有且只有一条直线
与这条直线平行
平行于同一条直线的两条直线平行
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
概念
同位角:在截线同旁,被截线相同的一侧的两角.
内错角:在截线两旁,被截线之内的两角
同旁内角:在截线同旁,被截线之内的两角
同位角的边构成“F“形,内错角的边构成”Z“形,同旁内角的边构成”U“形.
判断直线平行的条件
图形
已知
结果
理由
同位角
内错角
同旁内角
a//b
a//b
a//b
同位角相等
两直线平行
内错角相等
两直线平行
同旁内角互补
两直线平行
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
平行线的判定
图形
已知
结果
理由
同位角
内错角
同旁内角
a//b
a//b
内错角相等
两直线平行
同旁内角互补
两直线平行
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
平行线的性质
a//b
同位角相等
两直线平行
a//b
同位角相等
两直线平行
a//b
同位角相等
两直线平行
a//b
两直线平行
同位角相等
同旁内角互补
a//b
两直线平行
平行线的性质
∠2=∠3
a//b
同位角相等
两直线平行
a//b
两直线平行
内错角相等
平行线的性质
条 件
结论
两直线平 行
同位角相 等
内错角相等
同旁内角互补
平行线的判定
同位角相等
内错角相等
同旁内角互补
两直线平行
线的关系
角的关系
角的关系
线的关系
判定
性质
平行线的性质和平行线的判定方法的
区 别 与 联 系
两直线平行
{
1.同位角相等
2.内错角相等
3.同旁内角互补
性质
判定
1.由_________得到___________的结论是平行线的判定;
请注意:
2.由____________得到______________的结论是平行线的性质.
用途:
用途:
角的关系
两直线平行
说明直线平行
两直线平行
角相等或互补
说明角相等或互补
已知: ∠AOB。
“作一个角等于已知角”
B
O
A
求作: ∠A’O’B’ 使∠A’O’B’=∠AOB。
O’
A’
(2) 以点O为圆心,
任意长为半径
交OA于点C,
(3) 以点O’为圆心,
画弧,
C
D
同样(OD)长为半径
画弧,
C’
(4) 以点C’为圆心,
CD长为半径
画弧,
D’
(5) 过点D’作射线O’B’.
B’
A’
O’
B’
∠A’O’B’就是所求的角.
作 法 示 范
(1) 作射线O’A’;
交OB于点D;
交O’A’于点C’;
交前面的弧于点D’ ,
作法演示
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
