【大单元教学】鲁教版2023年六年级大单元大教研 第五章基本平面图形,相交线和平行线 教学设计课件(38张PPT)
文档属性
| 名称 | 【大单元教学】鲁教版2023年六年级大单元大教研 第五章基本平面图形,相交线和平行线 教学设计课件(38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 15.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 09:08:29 | ||
图片预览









文档简介
(共38张PPT)
基本平面图形、相交线与平行线单元备课与案例设计
目 录
CONTENTS
学情分析
《标准》要求
单元目标
教学设计
学情分析
大概念
单元作业
(1)点、线、面、角
①通过实物和模型,了解从物体抽象出来的几何体、平面、直线 和点等概念。
②会比较线段的长短,理解线段的和、差,以及线段中点的意义。
③掌握基本事实:两点确定一条直线。
④掌握基本事实:两点之间线段最短。
⑤理解两点间距离的意义,能度量和表达两点间的距离。
⑥理解角的概念,能比较角的大小;认识度、分、秒等角的度量 单位,能进行简单的单位换算,会计算角的和、差。
⑦能用尺规作图:做一条线段等于已知线段,作一个角等于已知角
《标准》要求
(2)相交线与平行线
①理解概念,
②掌握3个基本事实
③探索并掌握性质定理和判定定理。
④能用三角板和直尺过已知直线外一点画这条直线的平行线和垂线
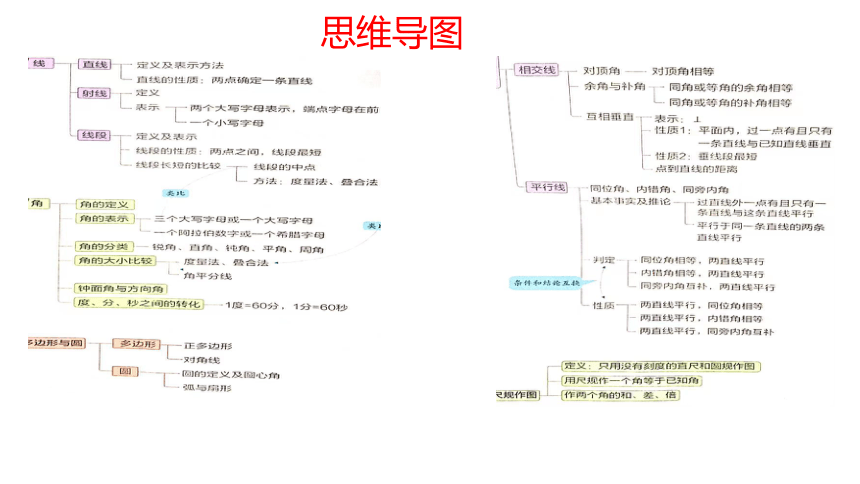
思维导图
对六年级的学生来说,小学已经接触过几何与图形,但是内容较简单。学生的思维停留在如何算,利用几个单纯的算式能求线段或角的度数,但不会有理有据的书写。
学情分析
1、认识简单平面图形,了解它们的含义及相关性质并能用符号表示
2. 会进行线段的长短或角的大小的比较,
3.能用尺规作图作一条线段等于一直线段,作一个角等于已知角
4.理解平行线及相关概念
5.掌握对顶角、补角的性质
6.掌握平行线的判定定理和性质定理
7.掌握三个基本事实
单元学习目标
教学设计(五单元)
专题1:平面图形的概念及特点(2课时)
专题2:比较线段长短和角的大小(2课时)
专题3:应用:握手问题和送贺卡问题(1课时)
专题1:平面图形的概念及表示方法(2课时)
概述:本专题的内容包括线段、射线、直线、角、多边形、扇形、弧、圆的相关概念及他们的表示,基本事实:两点确定一条直线
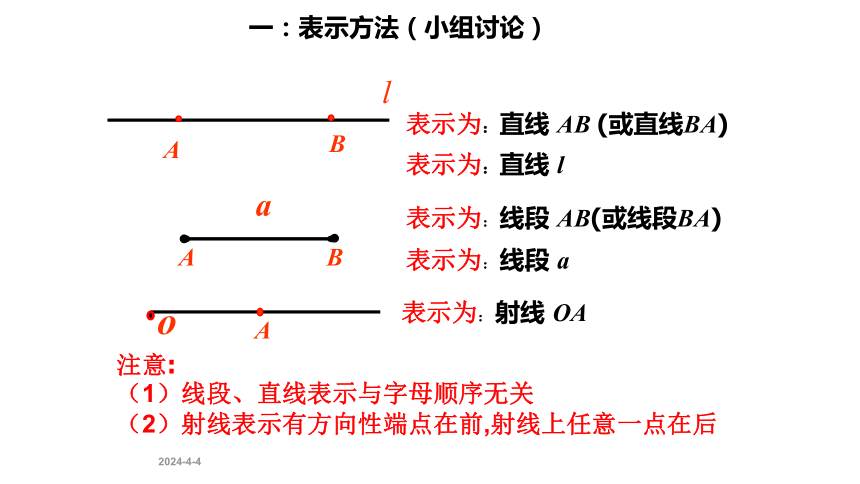
生活中的图形AB表示为:线段AB(或线段BA)a表示为:线段aAB表示为:直线AB(或直线BA)l表示为:直线lA表示为:射线OAo注意:(1)线段、直线表示与字母顺序无关(2)射线表示有方向性端点在前,射线上任意一点在后一:表示方法(小组讨论)2.线段、射线、直线的区别与联系(组内讨论)
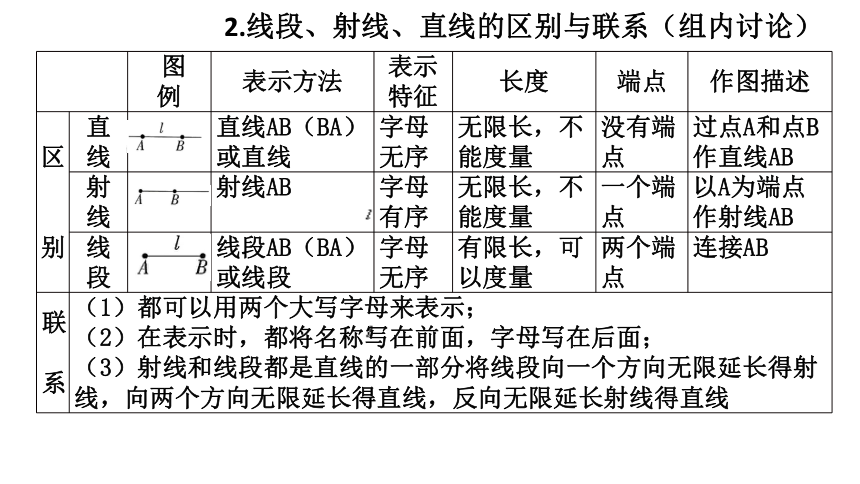
图 例 表示方法 表示特征 长度 端点 作图描述
区 别 直线 直线AB(BA)或直线 字母无序 无限长,不能度量 没有端点 过点A和点B作直线AB
射线 射线AB 字母有序 无限长,不能度量 一个端点 以A为端点作射线AB
线段 线段AB(BA)或线段 字母无序 有限长,可以度量 两个端点 连接AB
联 系 (1)都可以用两个大写字母来表示; (2)在表示时,都将名称写在前面,字母写在后面; (3)射线和线段都是直线的一部分将线段向一个方向无限延长得射线,向两个方向无限延长得直线,反向无限延长射线得直线 (3)如果你想将一根细木条固定在墙上,至少需要几个钉子?经过两点有且只有一条直线.直线的基本性质:简述为:两点确定一条直线。存在性唯一性专题二:比较线段长短和角的大小
5.3比较线段的长短
执教教师:
如图,从A地到C地有四条道路,如果你想从A地到C地,你会选择哪一条?
这说明了一个什么道理?
两点之间的所有连线中,线段最短.
两点之间,线段最短.
探 索 新 知---线段性质
探索新知---比较线段的长短
怎样比较两条线段的长短?
a
已知线段a,请用圆规、直尺作一条线段AC ,使AC=a。
1、作射线AB
2、在射线AB上,截取AC=a。
A
B
C
那么线段AC就是所求作的线段。
只用没有刻度的直尺和圆规画图称为尺规作图
动 手 操 作
如图,点M 把线段AB分成相等的两条线段AM与BM,点M 叫做线段AB的中点.(中点在线段上)
3.线段的中点
专题三:应用:握手问题和送贺卡问题
例1:如图所示,一条直线上的点数与线段的条数有如下关系:当一条直线上有三个点时,线段的条数为3,当一条直线上有4个点时,线段的条数为6,当一条直线上有5个点时,线段的条数为10……
(1)当一条直线上有6个点时,线段的条数为_____;
(2)当一条直线上有n个点时,线段的条数为多少?
3条射线
4条射线
5条射线
6条射线
B
F
K
P
这些图中分别有几个角 若有n条射线呢
3个
6个
10个
15个
拓展延伸
若有n条射线组成的图形,则共有 个角。
n(n-1)
2
例2:6(1)班有51人,如果每两人握手一次,共握手多少次?
如果每两人互相送贺卡,共送多少张?
教学设计(七单元)
专题1:两直线的位置关系(2课时)
专题2:平行线的判定和性质(4课时)
专题1:两直线的位置关系(2课时)
生活中的平行线与相交线
如图所示,直线AB和直线CD交于点O.
3
2
1
4
A
B
C
D
探究发现(对顶角)
问题1:观察图形,∠1和∠2的位置有什么关系?小组交流.
还有别的对顶角么?
直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,这样的两个角叫做对顶角.
O
如图所示,直线AB和直线CD交于点O.
3
2
1
4
A
B
C
D
探究发现(对顶角的性质)
问题2:观察图形,∠1和∠2的大小有什么关系?为什么?
对顶角相等
∵∠1+∠4=180°,∠2+∠4=180°
∴∠1+∠4=∠2+∠4
∴∠1=∠2(等式的基本性质)
O
如图所示,直线AB和直线CD交于点O.
3
2
1
4
A
B
C
D
探究发现(补角和余角)
问题3:观察图形,∠1和∠3有什么数量关系?
类似地,如果两个角的和是90°,那么称这两个角互为余角.
如果两个角的和是180°,那么称这两个角互为补角.
互补和互余都是两个角的数量关系,与位置无关.
∠1与∠3互为补角(互补),∠2与∠3互补…
O
专题2:平行线的判定和性质(4课时)
图7—3
小组合作交流,解决下列问题:在图7—4中
问题1:∠3与∠4有什么关系?为什么?
问题2:哪些角互为补角?哪些角互为余角?
问题3:∠AOC与∠BOD有什么关系?为什么?
N
2
D
C
O
1
3
4
A
B
图7-4
打台球时,选择适当的方向,用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,将图7-3抽象成图7-4,ON与DC交于点O,∠DON=∠CON=900,∠1=∠2.
同角或等角的余角相等,同角或等角的补角相等
探究发现(补角和余角的性质)
F
1
3
7
5
2
4
8
6
D
C
A
B
E
同位角的定义
如图,具有∠1与∠2这样位置关系的角称为同位角.
请找出图中其他的同位角.
∠3与∠4、∠5与∠6、∠7与∠8
你能说出同位角的特征吗
2
1
c
上图是木条转动过程中的3种情况,你发现木条 a 与木条 b 的位置关系发生了什么变化?木条 a 何时与木条 b 平行?
(1)
(2)
(3)
b
b
b
c
c
a
a
a
1
1
2
2
探究新知
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
当∠1>∠2时
当∠1=∠2时
当∠1>∠2时
①直线a和b不平行
当∠1=∠2时
②直线a和b平行
当∠1<∠2时
③直线a和b不平行
判断两条直线平行的方法:
两条直线被第三条直线所截,如果同位角相等,那么两直线平行.简称为:同位角相等,两直线平行.
(1)你能过直线 AB 外一点 P 画直线 AB 的平行线吗?
能画出几条?
过直线外一点有且只有一条直线与这条直线平行.
(2)在右图中,分别过点C,D画直线 AB 的平行线EF,GH.
EF与GH有怎样的位置关系?
平行于同一条直线的两条直线平行.
(1)你能过直线 AB 外一点 P 画直线 AB 的平行线吗?
能画出几条?
(2)在右图中,分别过点C,D画直线 AB 的平行线EF,GH.
EF与GH有怎样的位置关系?
A
B
.
C
.
D
也就是说:如果b//a,c//a, 那么b//c.
E
F
G
H
学习新知
a
b
c
过直线外一点有且只有一条直线与这条直线平行.
平行于同一条直线的两条直线平行.
评价内容:
(1)掌握基础知识和基本定理
(2)活学活用,体会数学知识在现实生活中应用的广 泛性
评价指标:出示练习,看学生掌握情况。
评价方法:小组互评,教师点评,
分层布置作业,小组间互评、教师点评
单元作业评价
谢 谢 指 导
基本平面图形、相交线与平行线单元备课与案例设计
目 录
CONTENTS
学情分析
《标准》要求
单元目标
教学设计
学情分析
大概念
单元作业
(1)点、线、面、角
①通过实物和模型,了解从物体抽象出来的几何体、平面、直线 和点等概念。
②会比较线段的长短,理解线段的和、差,以及线段中点的意义。
③掌握基本事实:两点确定一条直线。
④掌握基本事实:两点之间线段最短。
⑤理解两点间距离的意义,能度量和表达两点间的距离。
⑥理解角的概念,能比较角的大小;认识度、分、秒等角的度量 单位,能进行简单的单位换算,会计算角的和、差。
⑦能用尺规作图:做一条线段等于已知线段,作一个角等于已知角
《标准》要求
(2)相交线与平行线
①理解概念,
②掌握3个基本事实
③探索并掌握性质定理和判定定理。
④能用三角板和直尺过已知直线外一点画这条直线的平行线和垂线
思维导图
对六年级的学生来说,小学已经接触过几何与图形,但是内容较简单。学生的思维停留在如何算,利用几个单纯的算式能求线段或角的度数,但不会有理有据的书写。
学情分析
1、认识简单平面图形,了解它们的含义及相关性质并能用符号表示
2. 会进行线段的长短或角的大小的比较,
3.能用尺规作图作一条线段等于一直线段,作一个角等于已知角
4.理解平行线及相关概念
5.掌握对顶角、补角的性质
6.掌握平行线的判定定理和性质定理
7.掌握三个基本事实
单元学习目标
教学设计(五单元)
专题1:平面图形的概念及特点(2课时)
专题2:比较线段长短和角的大小(2课时)
专题3:应用:握手问题和送贺卡问题(1课时)
专题1:平面图形的概念及表示方法(2课时)
概述:本专题的内容包括线段、射线、直线、角、多边形、扇形、弧、圆的相关概念及他们的表示,基本事实:两点确定一条直线
生活中的图形AB表示为:线段AB(或线段BA)a表示为:线段aAB表示为:直线AB(或直线BA)l表示为:直线lA表示为:射线OAo注意:(1)线段、直线表示与字母顺序无关(2)射线表示有方向性端点在前,射线上任意一点在后一:表示方法(小组讨论)2.线段、射线、直线的区别与联系(组内讨论)
图 例 表示方法 表示特征 长度 端点 作图描述
区 别 直线 直线AB(BA)或直线 字母无序 无限长,不能度量 没有端点 过点A和点B作直线AB
射线 射线AB 字母有序 无限长,不能度量 一个端点 以A为端点作射线AB
线段 线段AB(BA)或线段 字母无序 有限长,可以度量 两个端点 连接AB
联 系 (1)都可以用两个大写字母来表示; (2)在表示时,都将名称写在前面,字母写在后面; (3)射线和线段都是直线的一部分将线段向一个方向无限延长得射线,向两个方向无限延长得直线,反向无限延长射线得直线 (3)如果你想将一根细木条固定在墙上,至少需要几个钉子?经过两点有且只有一条直线.直线的基本性质:简述为:两点确定一条直线。存在性唯一性专题二:比较线段长短和角的大小
5.3比较线段的长短
执教教师:
如图,从A地到C地有四条道路,如果你想从A地到C地,你会选择哪一条?
这说明了一个什么道理?
两点之间的所有连线中,线段最短.
两点之间,线段最短.
探 索 新 知---线段性质
探索新知---比较线段的长短
怎样比较两条线段的长短?
a
已知线段a,请用圆规、直尺作一条线段AC ,使AC=a。
1、作射线AB
2、在射线AB上,截取AC=a。
A
B
C
那么线段AC就是所求作的线段。
只用没有刻度的直尺和圆规画图称为尺规作图
动 手 操 作
如图,点M 把线段AB分成相等的两条线段AM与BM,点M 叫做线段AB的中点.(中点在线段上)
3.线段的中点
专题三:应用:握手问题和送贺卡问题
例1:如图所示,一条直线上的点数与线段的条数有如下关系:当一条直线上有三个点时,线段的条数为3,当一条直线上有4个点时,线段的条数为6,当一条直线上有5个点时,线段的条数为10……
(1)当一条直线上有6个点时,线段的条数为_____;
(2)当一条直线上有n个点时,线段的条数为多少?
3条射线
4条射线
5条射线
6条射线
B
F
K
P
这些图中分别有几个角 若有n条射线呢
3个
6个
10个
15个
拓展延伸
若有n条射线组成的图形,则共有 个角。
n(n-1)
2
例2:6(1)班有51人,如果每两人握手一次,共握手多少次?
如果每两人互相送贺卡,共送多少张?
教学设计(七单元)
专题1:两直线的位置关系(2课时)
专题2:平行线的判定和性质(4课时)
专题1:两直线的位置关系(2课时)
生活中的平行线与相交线
如图所示,直线AB和直线CD交于点O.
3
2
1
4
A
B
C
D
探究发现(对顶角)
问题1:观察图形,∠1和∠2的位置有什么关系?小组交流.
还有别的对顶角么?
直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,这样的两个角叫做对顶角.
O
如图所示,直线AB和直线CD交于点O.
3
2
1
4
A
B
C
D
探究发现(对顶角的性质)
问题2:观察图形,∠1和∠2的大小有什么关系?为什么?
对顶角相等
∵∠1+∠4=180°,∠2+∠4=180°
∴∠1+∠4=∠2+∠4
∴∠1=∠2(等式的基本性质)
O
如图所示,直线AB和直线CD交于点O.
3
2
1
4
A
B
C
D
探究发现(补角和余角)
问题3:观察图形,∠1和∠3有什么数量关系?
类似地,如果两个角的和是90°,那么称这两个角互为余角.
如果两个角的和是180°,那么称这两个角互为补角.
互补和互余都是两个角的数量关系,与位置无关.
∠1与∠3互为补角(互补),∠2与∠3互补…
O
专题2:平行线的判定和性质(4课时)
图7—3
小组合作交流,解决下列问题:在图7—4中
问题1:∠3与∠4有什么关系?为什么?
问题2:哪些角互为补角?哪些角互为余角?
问题3:∠AOC与∠BOD有什么关系?为什么?
N
2
D
C
O
1
3
4
A
B
图7-4
打台球时,选择适当的方向,用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,将图7-3抽象成图7-4,ON与DC交于点O,∠DON=∠CON=900,∠1=∠2.
同角或等角的余角相等,同角或等角的补角相等
探究发现(补角和余角的性质)
F
1
3
7
5
2
4
8
6
D
C
A
B
E
同位角的定义
如图,具有∠1与∠2这样位置关系的角称为同位角.
请找出图中其他的同位角.
∠3与∠4、∠5与∠6、∠7与∠8
你能说出同位角的特征吗
2
1
c
上图是木条转动过程中的3种情况,你发现木条 a 与木条 b 的位置关系发生了什么变化?木条 a 何时与木条 b 平行?
(1)
(2)
(3)
b
b
b
c
c
a
a
a
1
1
2
2
探究新知
当∠1>∠2时
当∠1=∠2时
当∠1<∠2时
当∠1>∠2时
当∠1=∠2时
当∠1>∠2时
①直线a和b不平行
当∠1=∠2时
②直线a和b平行
当∠1<∠2时
③直线a和b不平行
判断两条直线平行的方法:
两条直线被第三条直线所截,如果同位角相等,那么两直线平行.简称为:同位角相等,两直线平行.
(1)你能过直线 AB 外一点 P 画直线 AB 的平行线吗?
能画出几条?
过直线外一点有且只有一条直线与这条直线平行.
(2)在右图中,分别过点C,D画直线 AB 的平行线EF,GH.
EF与GH有怎样的位置关系?
平行于同一条直线的两条直线平行.
(1)你能过直线 AB 外一点 P 画直线 AB 的平行线吗?
能画出几条?
(2)在右图中,分别过点C,D画直线 AB 的平行线EF,GH.
EF与GH有怎样的位置关系?
A
B
.
C
.
D
也就是说:如果b//a,c//a, 那么b//c.
E
F
G
H
学习新知
a
b
c
过直线外一点有且只有一条直线与这条直线平行.
平行于同一条直线的两条直线平行.
评价内容:
(1)掌握基础知识和基本定理
(2)活学活用,体会数学知识在现实生活中应用的广 泛性
评价指标:出示练习,看学生掌握情况。
评价方法:小组互评,教师点评,
分层布置作业,小组间互评、教师点评
单元作业评价
谢 谢 指 导
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
