解直角三角形2[下学期]

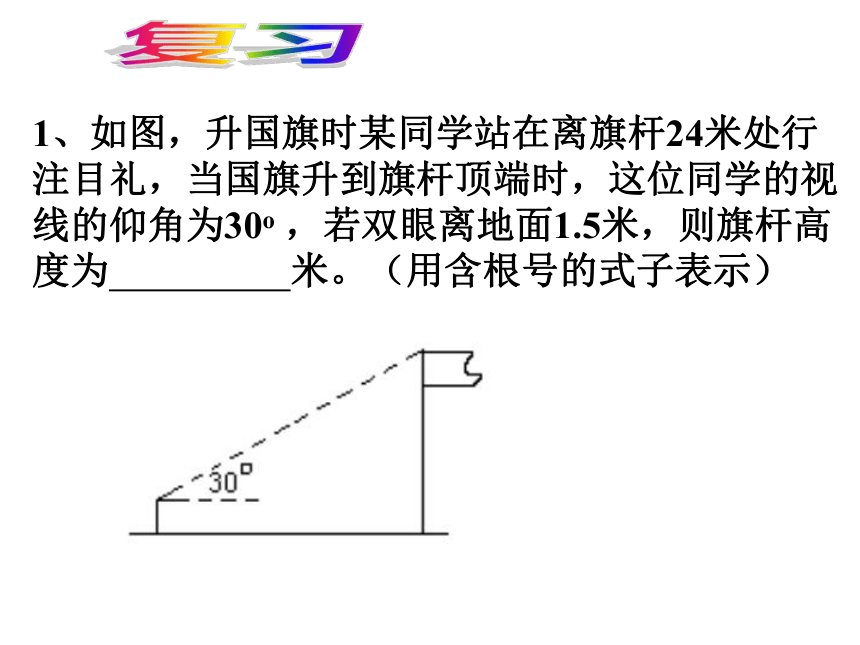
课件15张PPT。解直角三角形问题回顾在RtΔABC中，若∠C =900， 问题1. 在RtΔABC中,两锐角∠A, ∠B的有什么关系?答： ∠A+ ∠B= 900.问题2.在RtΔABC中，三边a、b、c的关系如何？答：a2+b2 =c2.问题3：在RtΔABC中， ∠A与边的关系是什么？答：解直角三角形问题分为两种情况：在Rt△ABC中，∠C=90°：　（3）已知∠A、 c, 则a=__________;b=_________。（4）已知∠A、 b, 则a=__________;c=_________。（5）已知∠A、 a，则b=__________;c=_________。（1）已知a、b，则c=__________。（2）已知a、c，则b=__________ 。复习（1）已知两条边，求其他边和角。（2）已知一条边和一个锐角，求其他边和角。1、如图，升国旗时某同学站在离旗杆24米处行注目礼，当国旗升到旗杆顶端时，这位同学的视线的仰角为30o ，若双眼离地面1.5米，则旗杆高度为 米。（用含根号的式子表示）复习
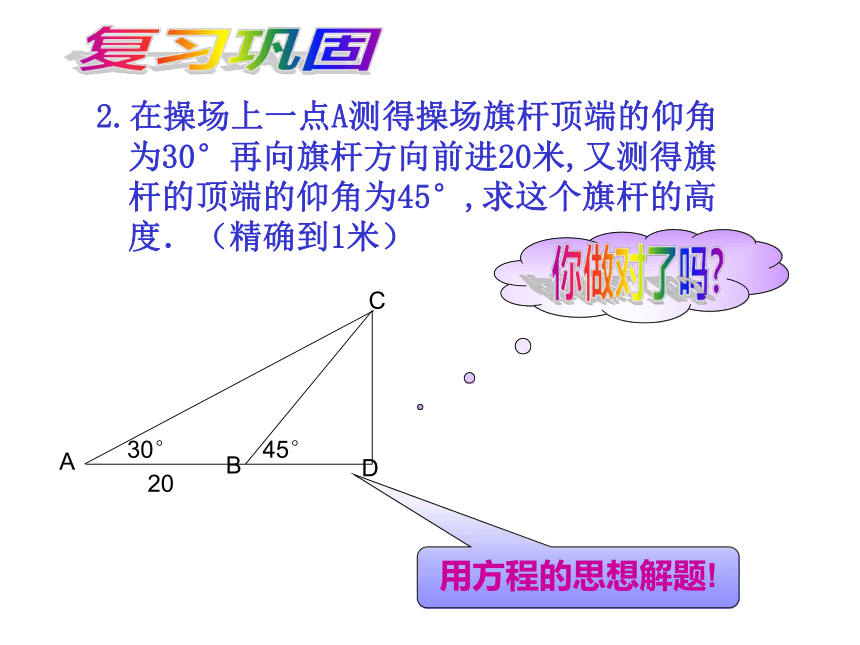
2.在操场上一点A测得操场旗杆顶端的仰角为30°再向旗杆方向前进20米,又测得旗杆的顶端的仰角为45°,求这个旗杆的高度．（精确到1米）
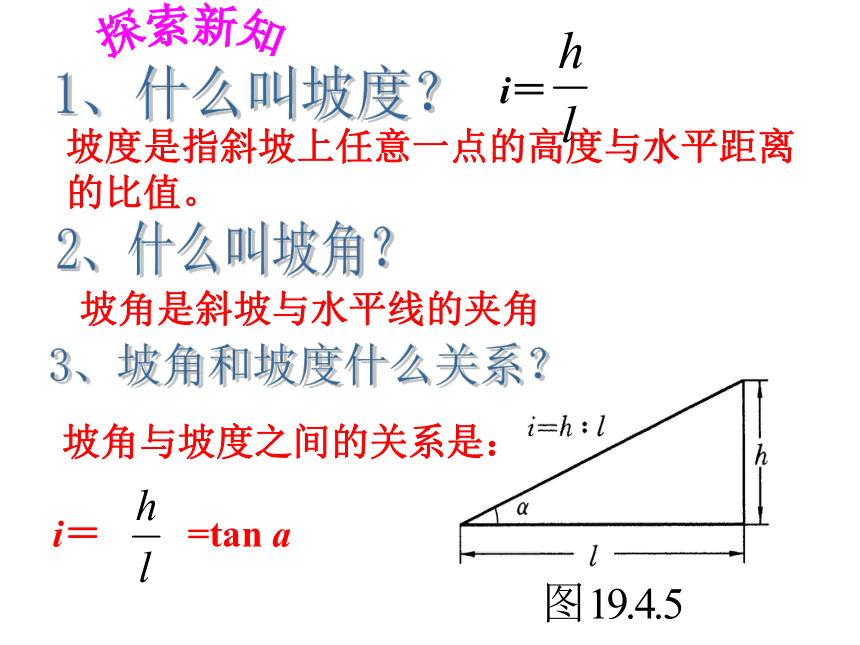
A20复习巩固用方程的思想解题!探索新知坡度是指斜坡上任意一点的高度与水平距离的比值。1、什么叫坡度？2、什么叫坡角？坡角是斜坡与水平线的夹角 3、坡角和坡度什么关系？ 坡角与坡度之间的关系是：
i＝ =tan a i＝⑴.一物体沿坡度为1:8的山坡向上移动 米，则物体升高了 米．
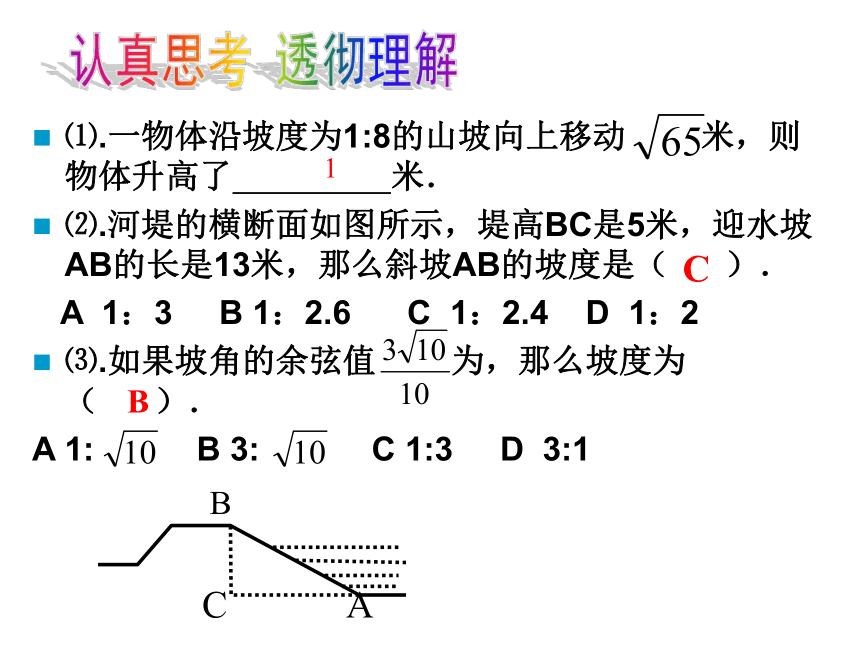
⑵.河堤的横断面如图所示，堤高BC是5米，迎水坡AB的长是13米，那么斜坡AB的坡度是（ ）．
A 1：3 B 1：2.6 C 1：2.4 D 1：2
⑶.如果坡角的余弦值 为，那么坡度为（ ）．
A 1: B 3: C 1:3 D 3:1认真思考 透彻理解1CB一段河坝的横断面为等腰梯形ABCD，试根据下图中的数据求出坡角α和坝底宽AD。（单位是米，结果保留根号）例1、问题研究坡度在日常生活中的应用也很广泛!如图，拦水坝的横断面为梯形ABCD，已知上底长CB=5米，迎水面坡度为1：
背水面坡度为1：1，坝高为4米．求：⑴坡底宽AD的长．⑵迎水坡CD的长．⑶坡角α、β．我最棒！例2、如图19.4.6，一段路基的横断面是梯形，高为4.2米，上底的宽是12.51米，路基的坡面与地面的倾角分别是32°和28°．求路基下底的宽．（精确到0.1米） 32°28°4.2米12.51米EF例3、⑴、一斜坡的坡角为30度，则它的坡度
为 ；
⑵、坡度通常写成1： 的形式。如果一个坡度为1 :1,则这个坡角为 ，
⑶、等腰梯形的较小底长为3，腰长为5，高为4，则另一个底长为 ，坡度为 ，
⑷、梯形的两底长分别为为5和8，一腰长为4，则另一腰长x的取值范围是 。达标反馈 1： m45094:31(选用数据:sin22°37′≈ ,cos22°37′ ≈ ,
tan 22°37′ ≈ ,
tan 32° ≈ )MN作业1. 教科书P 116. 习题 2. 2. 新课程 同步导学 19.4.35、如图，一铁路路基的横断面为等腰梯形，坡面AD的坡度为1：2，高为6米，则下底宽AB= 米。8、锐角ABC中， =0，
则= 。