解直角三角形（1）[下学期]

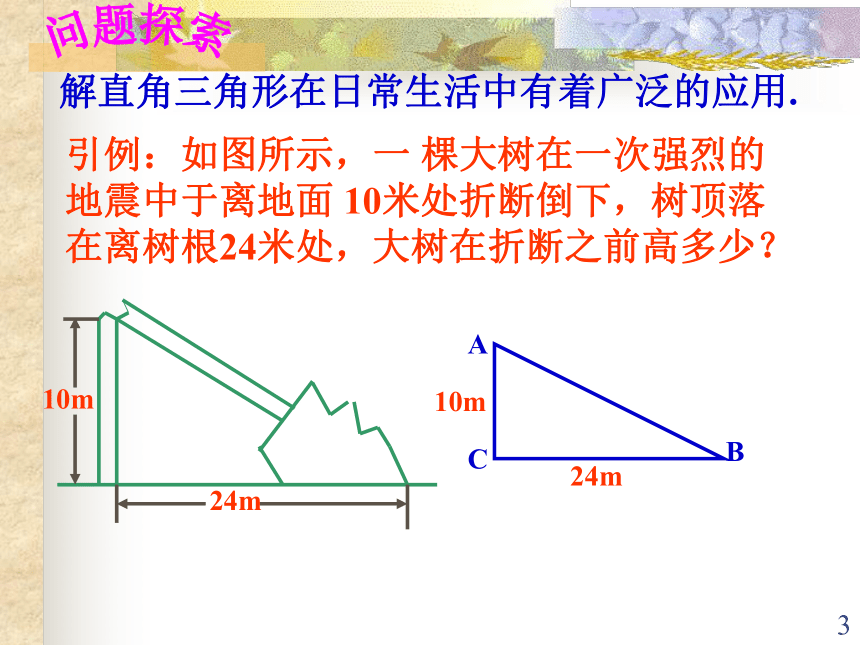
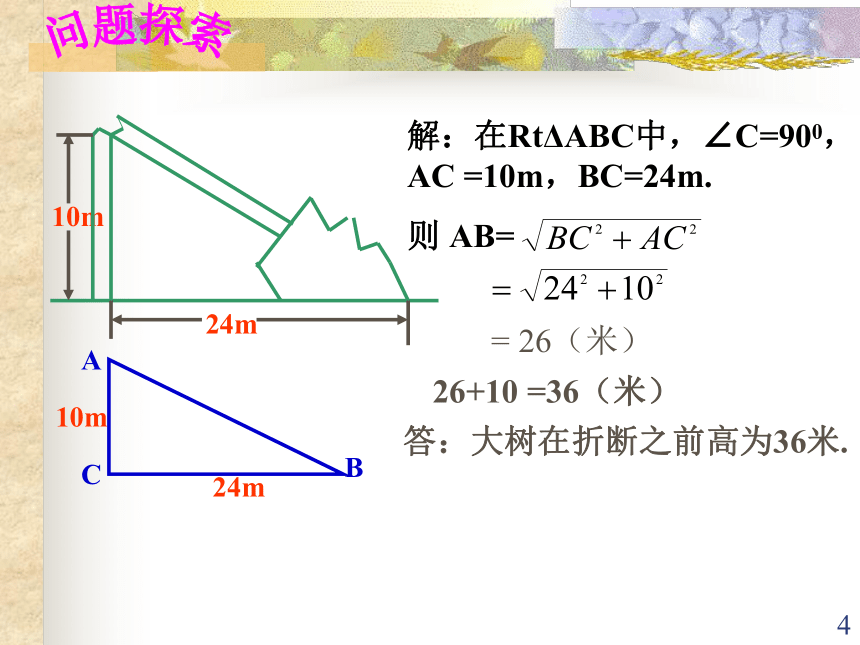
课件20张PPT。1解直角三角形2问题回顾(复习）在RtΔABC中，若∠C =900， 问题1. 在RtΔABC中，两锐角∠A、 ∠B的有什么关系？答： ∠A+ ∠B= 900.问题2.在RtΔABC中，三边a、b、c的关系如何？答：a2+b2 =c2.问题3：在RtΔABC中， ∠A与边的有什么关系？答：3问题探索解直角三角形在日常生活中有着广泛的应用.引例：如图所示，一 棵大树在一次强烈的地震中于离地面 10米处折断倒下，树顶落在离树根24米处，大树在折断之前高多少？ 10m4问题探索5什么是解直角三角形？
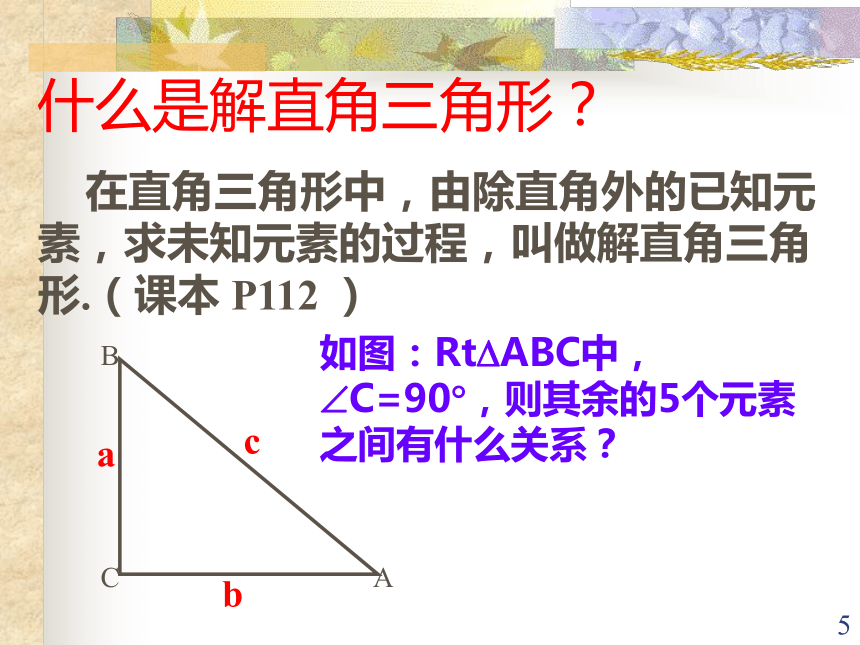
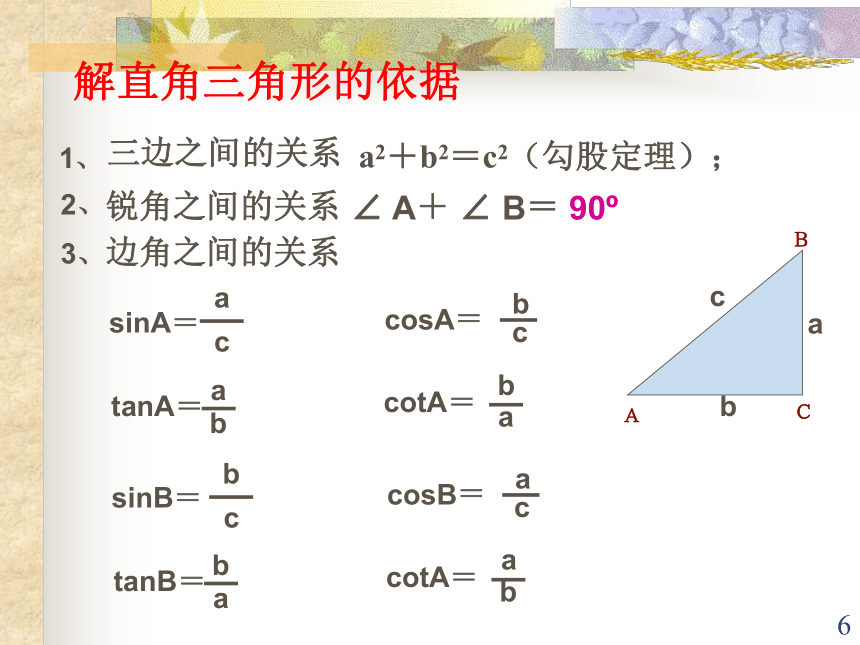
在直角三角形中，由除直角外的已知元素，求未知元素的过程，叫做解直角三角形.（课本 P112 ）如图：Rt?ABC中，?C=90?，则其余的5个元素之间有什么关系？b6789101112131.在Rt△ABC中，∠C＝90°，由下列条件解直角三角形：
(1)已知a＝6 ,b=6 ,则∠B= ，
∠A= ，c = ；
(2)已知c＝30,∠A＝60°则∠B= ，
a = ，b = ；
〖达标练习〗14问题探索例4.如图，东西两炮 台A、B相距2000米，同时发现入侵敌舰C，炮台A测得敌舰C在它的南偏东400的方向，炮台B测得敌舰C在它的正南方，试求敌舰与两炮台的距离.（精确到1米）15问题探索≈3111（米）
4002000解： ∵∠BAD =900 ∠CAD =400 ∴ ∠CAB =500 在RtΔABC中， ∵tan ∠CAB = 答：敌舰与A、B两炮台的距离分别约为3111米和2384米.∴ BC = AB·tan 500 ≈2000×1.192 ≈2384（米）
又∵cos ∠CAB =16注意 在解直角三角形的过程中，常会遇到近似计算，本书除特别说明外，边长保留四个有效数字，角度精确到1′.
解直角三角形，只有下面两种情况：
（1）已知两条边；
（2）已知一条边和一个锐角
17试一试在电线杆离地面8米高的地方向地面拉一条长10米的缆绳，问这条缆绳应固定在距离电线杆底部多远的地方？
2. 海船以32.6海里/时的速度向正北方向航行，在A处看灯塔Q在海船的北偏东30゜处，半小时后航行到B处，发现此时灯塔Q与海船的距离最短，求灯塔Q到B处的距离.（画出图形后计算，精确到0.1海里）
书 P 113. 1、 2.18什么是解直角三角形？
由直角三角形中除直角外的其余5个元素里已知2个元素，求未知3个元素的过程，叫做解直角三角形.（已知2个元素中至少有一个是边）如图：Rt?ABC中，?C=90?，则其余的5个元素之间关系是什么？b小结192、 我军某部在一次野外训练中，有一辆坦克准备通过一座小山，已知山脚和山顶的水平距离为1000米，山高为565米，如果这辆坦克能够爬300 的斜坡，试问：它能不能通过这座
小山？〖课后思考〗20课后作业：3、课本P116 习题19.4 14、课本P120 复习题 11