【大单元教学】鲁教版2023年七年级大单元 第七章 二元一次方程组 大教研课件(19张PPT)
文档属性
| 名称 | 【大单元教学】鲁教版2023年七年级大单元 第七章 二元一次方程组 大教研课件(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 391.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 09:31:24 | ||
图片预览






文档简介
(共19张PPT)
二元一次方程组
学习目标:
1.掌握二元一次方程(组)的基本概念以及会识别二元一次方程(组);
2.掌握二元一次方程(组)解的概念;
3.会用代入消元法加减消元法解二元一次方程组;
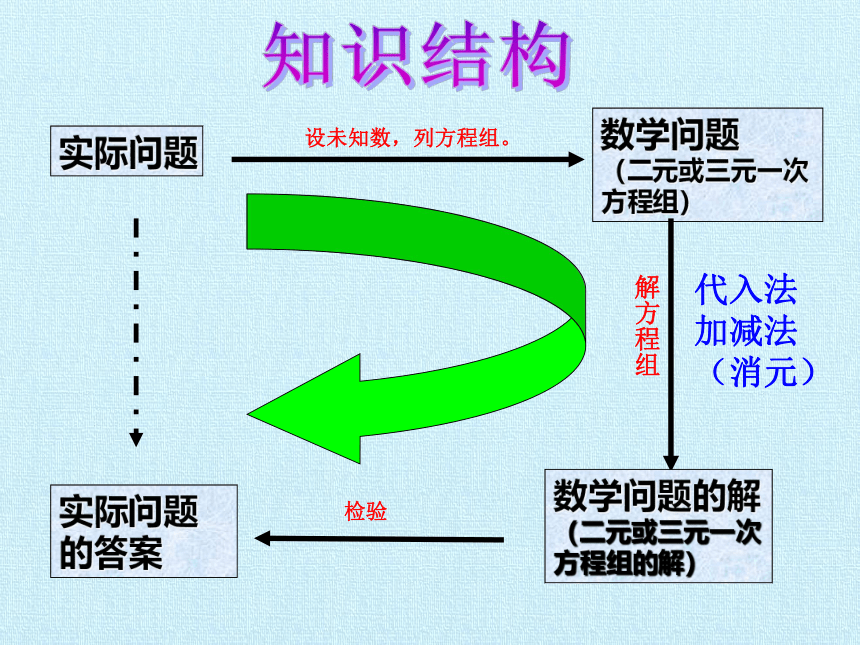
实际问题
设未知数,列方程组。
数学问题
(二元或三元一次方程组)
解方程组
数学问题的解
(二元或三元一次
方程组的解)
检验
实际问题的答案
代入法
加减法
(消元)
知识结构
一、二元一次方程(组)定义
有两个未知数且含未知数项的次数是一次的方程叫做二元一次方程。
1.什么是二元一次方程?
适合一个二元一次方程的一对未知数的值,叫做这个二元一次方程的一个解。
2.什么是二元一次方程组?
有两个一次方程组成,并且含有两个未知数的方程组叫做二元一次方程组。
一般地,在二元一次方程组中,使每个方程都适合的解(公共解),叫做这个二元一次方程组的解。
(2)2x+y+z=1
(5)2a+3b=5
(6)2x+10=0
(3)x2+y=20
(4)x2+2x+1=0
(1)2x+5y=10
1.请判断下列各方程中,哪些是二元一次方程,哪些不是?并说明理由。
2.下面4组数值中,哪些是二元一次方程2x+y=10的解?
x=-2
y=6
(1)
x=3
y=4
(2)
x=4
y=3
(3)
x=6
y=-2
(4)
3.方程x+2y=7在正整数范围内的解有( )
A.1个
B.2个
C.3个
D.无数个
C
4.若x2m-1+5y3n-2m=7是二元一次方程,则m=___,n=____。
1
1
5.下列是二元一次方程组的是( )
+y=3
x
1
2x+y=0
(A)
3x-1=0
2y=5
(B)
x+y=7
3y+z=4
(C)
5x-y=-2
3y+x=4
(D)
2
B
二、二元一次方程组的解法
1.解二元一次方程组的基本思想是什么?
二元一次方程组
一元一次方程
消元
转化
2.消元的方法有哪些?
代入消元法、加减消元法
例:关于x、y的二元一次方程组
的解与
的解相同,求a、b的值。
解:解方程组
得
将
代入方程组
得
解得
∴a= ,b=
审:审清题目中的等量关系。
设:设未知数。
列:根据等量关系,列出方程组。
解:解方程组,求出未知数。
验:检验所求出未知数是否符合题意,
答:写出答案
三、列二元一次方程组解实际问题的一般步骤
例:已知甲、乙两种商品的标价和为100元,因市场变化,甲商品打9折,乙商品提价5﹪,调价后,甲、乙两种商品的售价和比标价和提高了2﹪,求甲、乙两种商品的标价各是多少
解:设甲、乙两种商品的标价分别为x、y元,
根据题意,得
解这个方程组,得
答:甲种商品的标价是20元,乙种商品的标价是80元。
二元一次方程组和一次函数的图象的关系
方程组的解是对应的两条直线的交点坐标
两条线的交点坐标是对应的方程组的解
二元一次方程和一次函数的图象的关系
以二元一次方程的解为坐标的点都在对应的函数图象上。
一次函数图象上的点的坐标都适合对应的二元一次方程。
四、二元一次方程与一次函数:
例:(2015 齐齐哈尔)甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地。乙车从B地直达A地,两车同时到达A地。甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
(1)乙车的速度是 千米/时,t= 小时;
(2)直接写出乙车出发多长时间两车相距120千米。
分析:(1)首先根据图示,可得乙车的速度是60千米/时,然后根据路程÷速度=时间,用两地之间的距离除以乙车的速度,求出乙车到达A地用的时间是多少;最后根据路程÷时间=速度,用两地之间的距离除以甲车往返AC两地用的时间,求出甲车的速度,再用360除以甲车的速度,求出t的值是多少即可。
解:(1)根据图示,可得
乙车的速度是60千米/时,
甲车的速度是:(360×2)÷(480÷60﹣1﹣1)=720÷6
=120(千米/小时)
∴t=360÷120=3(小时)。
(2)根据题意,分3种情况:
①甲乙两车相遇之前相距120千米;②当甲车停留在C地时;
③两车都朝A地行驶时;然后根据路程÷速度=时间,分类讨论,
求出乙车出发多长时间两车相距120千米即可。
(2)①(480﹣60﹣120)÷(120+60)+1
=300÷180+1
= = (小时)
②当甲车停留在C地时,
(480﹣360+120)÷60
=240÷6
=4(小时)
③两车都朝A地行驶时,
设乙车出发x小时后两车相距120千米,
则60x﹣[120(x﹣1)﹣360]=120,
所以480﹣60x=120,
所以60x=360,
解得x=6。
综上,可得乙车出发
后两车相距120千米。
方程组 中,x与y的和12,求k的值。
解得:k=14
解法1:解这个方程组,得
依题意:x+y=12
所以(2k-6)+(4-k)=12
解法2:根据题意,得
解这个方程组,得k=14
大显身手
课堂小结
1.本节课,你学会了什么?
2.你还有什么疑惑吗?
1.求二元一次方程 的正整数解。
2.已知|2x+3y+5|+(3x+2y-25)2=0,则x-y=______。
3.解方程组
课后作业
4.先阅读材料,后解方程组。
材料:解方程组 时,
可由①得x-y=1③
将③代入②得4×1-y=5。 即y=-1。进一步得
这种解方程组的方法称为“整体代入法”。
请用整体代入法解方程组
①
②
大显身手
谢 谢
二元一次方程组
学习目标:
1.掌握二元一次方程(组)的基本概念以及会识别二元一次方程(组);
2.掌握二元一次方程(组)解的概念;
3.会用代入消元法加减消元法解二元一次方程组;
实际问题
设未知数,列方程组。
数学问题
(二元或三元一次方程组)
解方程组
数学问题的解
(二元或三元一次
方程组的解)
检验
实际问题的答案
代入法
加减法
(消元)
知识结构
一、二元一次方程(组)定义
有两个未知数且含未知数项的次数是一次的方程叫做二元一次方程。
1.什么是二元一次方程?
适合一个二元一次方程的一对未知数的值,叫做这个二元一次方程的一个解。
2.什么是二元一次方程组?
有两个一次方程组成,并且含有两个未知数的方程组叫做二元一次方程组。
一般地,在二元一次方程组中,使每个方程都适合的解(公共解),叫做这个二元一次方程组的解。
(2)2x+y+z=1
(5)2a+3b=5
(6)2x+10=0
(3)x2+y=20
(4)x2+2x+1=0
(1)2x+5y=10
1.请判断下列各方程中,哪些是二元一次方程,哪些不是?并说明理由。
2.下面4组数值中,哪些是二元一次方程2x+y=10的解?
x=-2
y=6
(1)
x=3
y=4
(2)
x=4
y=3
(3)
x=6
y=-2
(4)
3.方程x+2y=7在正整数范围内的解有( )
A.1个
B.2个
C.3个
D.无数个
C
4.若x2m-1+5y3n-2m=7是二元一次方程,则m=___,n=____。
1
1
5.下列是二元一次方程组的是( )
+y=3
x
1
2x+y=0
(A)
3x-1=0
2y=5
(B)
x+y=7
3y+z=4
(C)
5x-y=-2
3y+x=4
(D)
2
B
二、二元一次方程组的解法
1.解二元一次方程组的基本思想是什么?
二元一次方程组
一元一次方程
消元
转化
2.消元的方法有哪些?
代入消元法、加减消元法
例:关于x、y的二元一次方程组
的解与
的解相同,求a、b的值。
解:解方程组
得
将
代入方程组
得
解得
∴a= ,b=
审:审清题目中的等量关系。
设:设未知数。
列:根据等量关系,列出方程组。
解:解方程组,求出未知数。
验:检验所求出未知数是否符合题意,
答:写出答案
三、列二元一次方程组解实际问题的一般步骤
例:已知甲、乙两种商品的标价和为100元,因市场变化,甲商品打9折,乙商品提价5﹪,调价后,甲、乙两种商品的售价和比标价和提高了2﹪,求甲、乙两种商品的标价各是多少
解:设甲、乙两种商品的标价分别为x、y元,
根据题意,得
解这个方程组,得
答:甲种商品的标价是20元,乙种商品的标价是80元。
二元一次方程组和一次函数的图象的关系
方程组的解是对应的两条直线的交点坐标
两条线的交点坐标是对应的方程组的解
二元一次方程和一次函数的图象的关系
以二元一次方程的解为坐标的点都在对应的函数图象上。
一次函数图象上的点的坐标都适合对应的二元一次方程。
四、二元一次方程与一次函数:
例:(2015 齐齐哈尔)甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地。乙车从B地直达A地,两车同时到达A地。甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
(1)乙车的速度是 千米/时,t= 小时;
(2)直接写出乙车出发多长时间两车相距120千米。
分析:(1)首先根据图示,可得乙车的速度是60千米/时,然后根据路程÷速度=时间,用两地之间的距离除以乙车的速度,求出乙车到达A地用的时间是多少;最后根据路程÷时间=速度,用两地之间的距离除以甲车往返AC两地用的时间,求出甲车的速度,再用360除以甲车的速度,求出t的值是多少即可。
解:(1)根据图示,可得
乙车的速度是60千米/时,
甲车的速度是:(360×2)÷(480÷60﹣1﹣1)=720÷6
=120(千米/小时)
∴t=360÷120=3(小时)。
(2)根据题意,分3种情况:
①甲乙两车相遇之前相距120千米;②当甲车停留在C地时;
③两车都朝A地行驶时;然后根据路程÷速度=时间,分类讨论,
求出乙车出发多长时间两车相距120千米即可。
(2)①(480﹣60﹣120)÷(120+60)+1
=300÷180+1
= = (小时)
②当甲车停留在C地时,
(480﹣360+120)÷60
=240÷6
=4(小时)
③两车都朝A地行驶时,
设乙车出发x小时后两车相距120千米,
则60x﹣[120(x﹣1)﹣360]=120,
所以480﹣60x=120,
所以60x=360,
解得x=6。
综上,可得乙车出发
后两车相距120千米。
方程组 中,x与y的和12,求k的值。
解得:k=14
解法1:解这个方程组,得
依题意:x+y=12
所以(2k-6)+(4-k)=12
解法2:根据题意,得
解这个方程组,得k=14
大显身手
课堂小结
1.本节课,你学会了什么?
2.你还有什么疑惑吗?
1.求二元一次方程 的正整数解。
2.已知|2x+3y+5|+(3x+2y-25)2=0,则x-y=______。
3.解方程组
课后作业
4.先阅读材料,后解方程组。
材料:解方程组 时,
可由①得x-y=1③
将③代入②得4×1-y=5。 即y=-1。进一步得
这种解方程组的方法称为“整体代入法”。
请用整体代入法解方程组
①
②
大显身手
谢 谢
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
