直角三角形全等的判定[上学期]

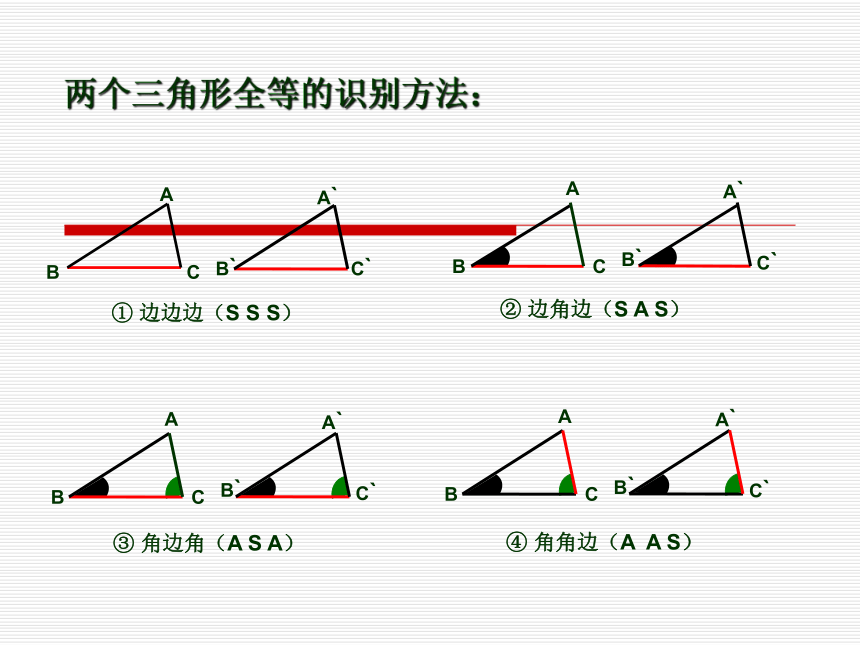
课件14张PPT。直角三角形全等的识别① 边边边（S S S）④ 角角边（A A S）③ 角边角（A S A）② 边角边（S A S）两个三角形全等的识别方法：三角形全等的判定想一想:
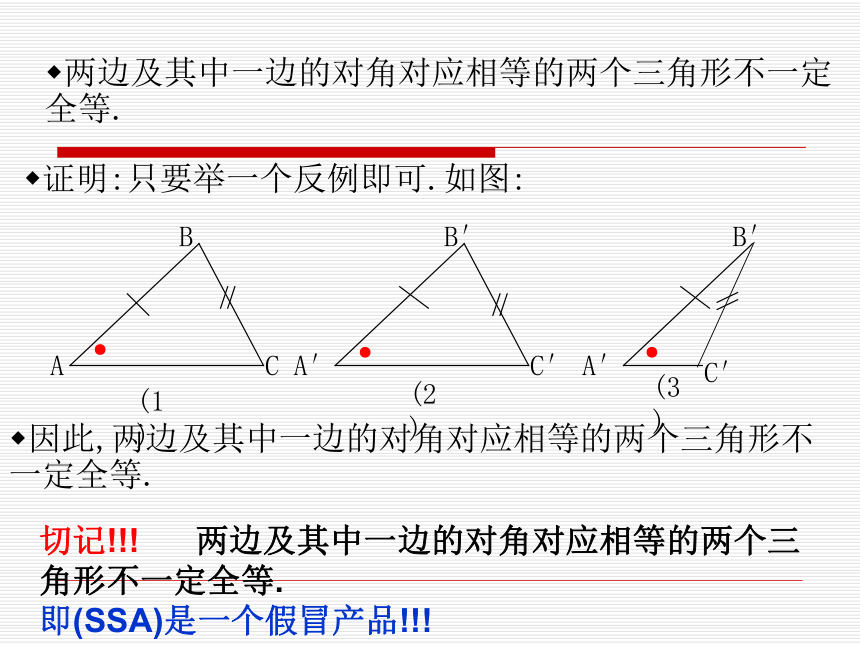
两边及其中一边的对角对应相等的两个三角形全等?两边及其中一边的对角对应相等的两个三角形不一定全等.两边及其中一边的对角对应相等的两个三角形不一定全等.证明:只要举一个反例即可.如图:因此,两边及其中一边的对角对应相等的两个三角形不一定全等.切记!!! 两边及其中一边的对角对应相等的两个三角形不一定全等.
即(SSA)是一个假冒产品!!!三角形全等的判定两边及其中一边的对角对应相等的两个三角形不一定全等.如果其中一边的所对的角是直角呢?两边及其中一边的对角对应相等的两个三角形不一定全等.但如果其中一边的所对的角是直角,那么这两个三角形全等.已知:如图,在△ABC和△A′B′C′中, AC=A′C ′,
AB=A′B′, ∠C=∠C′=900.
求证:△ABC≌△A′B′C′.直角三角形全等的判定定理定理: 斜边和一条直角边对应相等的两个直角三角形全
等(斜边,直角边或HL).如图,在△ABC和△A′B′C′中, ∠C=∠C′=900 ,
∵ AC=A′C ′

AB=A′B′ ∴Rt△ABC≌Rt△A′B′C′(HL).
知识在于积累判断下列命题的真假,并说明理由:两个锐角对应相等的两个直角三角形全等;斜边及一个锐角对应相等的两个直角三角形全等;两直角边对应相等的两个直角三角形全等;一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等.一个角和一条直角分别相等的两个直角三角形全等.1.已知:如图,D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且DE=DF.
求证: △ABC是等腰三角形. 老师期望:请将证明过程规范化书写出来. 2.已知:如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为E,F,DE=BF.
求证:(1)AE=AF (2)AB∥CD. 老师期望:请将证明过程规范化书写出来. 3、已知BE和CF是△ABC的高， BE＝CF，H是BE和CF的交点。求证：HB＝HC。ABCEFH如图， AB是圆O的直径， ∠ 1 = ∠ 2 ，
试说明△ABC≌△ABD12回味无穷直角三角形全等的判定定理:
1.斜边和一条直角边对应相等的两个直角三角形全等(斜 边,直角边或H.L.).
2.三边对应相等的两个三角形全等（S.S.S.）.
3.两边及其夹角对应相等的两个三角形全等（S.A.S.）.
4.两角及其夹边对应相等的两个三角形全等（A.S.A.）.
5.两角及其中一角的对边对应相等的两个三角形全等（A.A.S.）.
综上所述,直角三角形全等的判定条件可归纳为:
一边及一个锐角对应相等的两个直角三角形全等;
两边对应相等的两个直角三角形全等;
切记!!! 两边及其中一边的对角对应相等的两个三角形不一定全等.
即(SSA)是一个假冒产品!!!结束寄语严格性之于数学家,犹如道德之于人.
证明的规范性在于：条理清晰，因果相应,言必有据.这是初学证明者谨记和遵循的原则.