【大单元教学】鲁教版2023年九年级大单元教学 第五章《圆》 课件(21张PPT)
文档属性
| 名称 | 【大单元教学】鲁教版2023年九年级大单元教学 第五章《圆》 课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 10:03:34 | ||
图片预览





文档简介
(共21张PPT)
《圆》大单元教学设计
01
对照课标
03
教学设计
02
教材分析
目录
1
对照课标
1.面向全体学生,注重个体差异,使不同的人在数学上得到相应的发展。
2.课程要反映社会的需要、数学的特点,对内容进行结构化整合,探索发展学生核心素养的路径。
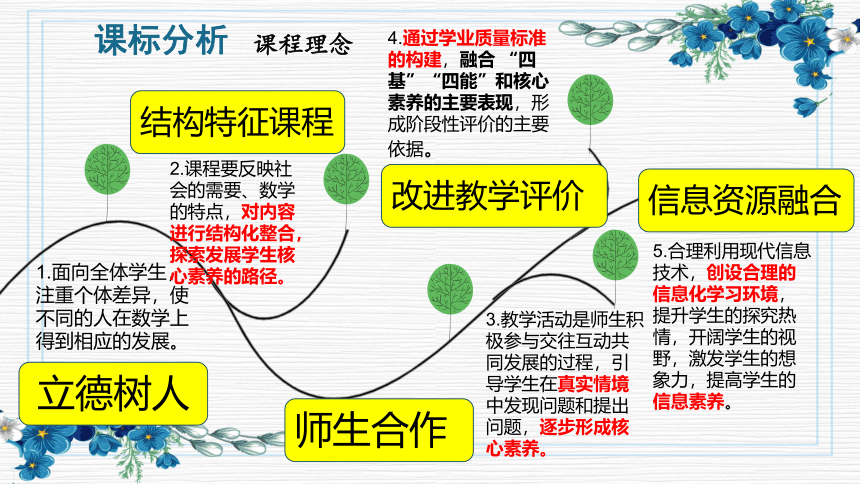
课标分析
3.教学活动是师生积极参与交往互动共同发展的过程,引导学生在真实情境中发现问题和提出问题,逐步形成核心素养。
4.通过学业质量标准的构建,融合 “四基”“四能”和核心素养的主要表现,形成阶段性评价的主要依据。
5.合理利用现代信息技术,创设合理的信息化学习环境,提升学生的探究热情,开阔学生的视野,激发学生的想象力,提高学生的信息素养。
立德树人
结构特征课程
改进教学评价
师生合作
信息资源融合
课程理念
单元总目标
对照《课标》
①理解圆、弧、弦、圆心角、圆周角的概念,了解等圆、等弧的概念;探索并掌握点与圆的位置关系。
②探索并证明垂径定理:垂直于弦的直径平分弦以及弦所对的两条弧。
③探索圆周角与圆心角及其所对弧的关系,知道同弧(或等弧) 所对的圆周角相等。了解并证明圆周角定理及其推论:圆周角等于它 所对弧上的圆心角的一半;直径所对的圆周角是直角,90°的圆周角 所对的弦是直径;圆内接四边形的对角互补。
④了解三角形的内心与外心。
⑤了解直线与圆的位置关系,掌握切线的概念。
⑥能用尺规作图:过不在同一直线上的三点作圆;作三角形的外接圆、内切圆;作圆的内接正方形和内接正六边形。
⑦*能用尺规作图:过圆外一点作圆的切线。
⑧*探索并证明切线长定理:过圆外一点的两条切线长相等。
⑨会计算圆的弧长、扇形的面积。
⑩了解正多边形的概念及正多边形与圆的关系。
2
教材分析
本单元属于图形与几何板块的图形的认识方面的内容。学生在第一学段已经直观地认识了圆,并学习了长方形、正方形等平面图形以及它们的周长、面积计算,在此基础上本单元进一步学习圆的知识,为以后学习圆柱、圆锥等知识和绘制简单扇形统计图打好基础。
本单元学习的圆是一种曲线图形,和以前学的直线图形在性质上有很大的不同,但在研究方法上,联系又很紧密。学生学习这部分知识时,要留给他们充分的思考与探究空间,让学生重点体会“化曲为直”“化圆为方”等转化的数学思想,以及无限逼近的“极限思想”等。
教材分析
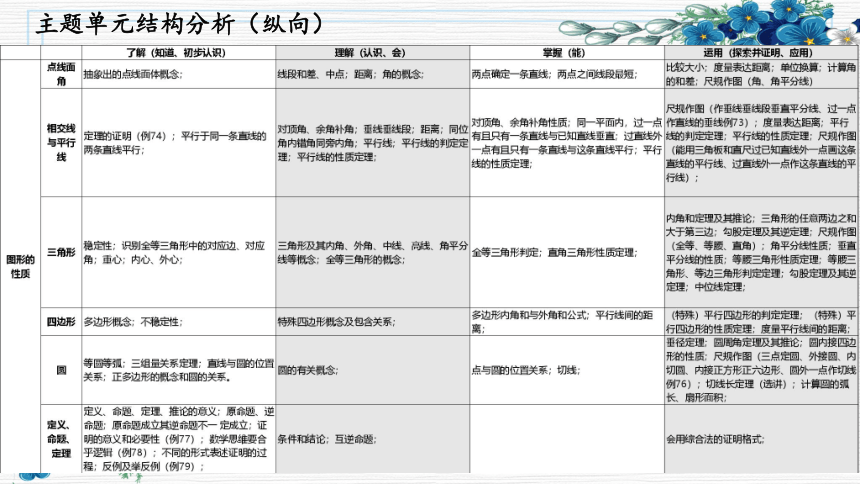
主题单元结构分析(纵向)
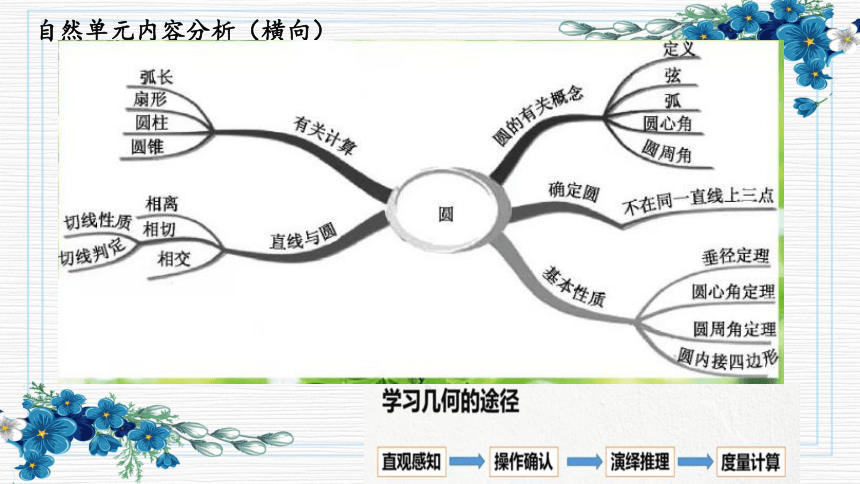
自然单元内容分析(横向)
3
单元教学设计
字符延长
二
教学重难点
三
学情分析
一
教学思路
四
教学建议
五
单元整体规划
一、单元教学设计思路
圆是平面几何中基本的图形之一,它不仅在几何中有重要地位,而且是进一步学习其他数学知识的重要基础。本章是在小学学过的圆的基础知识上,系统的研究圆的概念、性质、与圆有关的位置关系,正多边形和圆,圆的有关计算及证明。
与“直线形’’图形相比,圆具有独特的对称性。它不仅是轴对称图形,而且是中心对称图形,垂径定理、切线长定理都是圆的对称性的具体表现,可以通过圆的对称性来研究这些内容。
《圆》这一章的教学是初中平面几何中最为复杂的,其中包含了圆自身众多构成要素和相关要素之间的性质,而它的研究方法又和以前研究图形的方法有着相似之处,所以这一章的学习可以借鉴前面研究图形的经验。例如,圆的对称性所产生的性质,参照等腰三角形和平行四边形研究的经验,这样既帮助学生降低了难度,也为他们搭建了探究的平台;圆与其他图形的位置关系的问题之间有相互借鉴价值的,这些都需要在教学过程中加以凸显,让学生在学习过程中体会几何学习的方法。感悟图形研究的途径,从而对今后的数学学习产生深远影响。
二、教学重难点
(1)理解圆、弧、弦、圆心角、圆周角的概念,了解等圆、等弧的概念;掌握点与圆的位置关系。
(2)掌握垂径定理及其推论,并能用垂径定理解决相关问题。
(3)掌握圆周角与圆心角及其所对弧的关系,掌握圆周角定理及其推论。
(4)了解道三角形的内心和外心,掌握内心和外心的位置。
(5)理解直线和圆的位置关系,掌握切线的概念。
(6)掌握切线的判定方法及其性质
(7)掌握切线长定理
(8)了解圆与圆的位置关系。
(9)了解正多边形的概念及正多边形与圆的关系。
(10)会计算圆的弧长、扇形的面积。
三、学情分析
学生在学习本章之前,已通过折叠、对称、平移旋转、推理证明等方式认识了许多图形的性质,积累了大量的空间与图形的经验.本章是在学习了这些直线形的有关性质的基础上,进一步来探索一种特殊的曲线──圆的有关性质,而且把直线形里学过的的一些基本图形,几何变换加以灵活运用.通过本章的学习,学生会对圆有一个较为全面系统的认识,而且对各种数学思想如分类讨论,转化思想,完全归纳、类比的思想等有很好的理解和把握。
四、教学建议
本章是在学习了直线型图形的有关性质和证明的基础上,来探索一种最简单、最常见的曲线型图形——圆的有关性质,在学习这一章之前,学生已经通过折纸、对称、平移、旋转、推理证明等方式认识了许多图形的性质.在本章的设计中,充分利用了学生的已有经验.例如,采用折叠、旋转的方法探索圆的对称性;利用轴对称变换的方法探索垂径定理及其逆定理;用旋转变换的方法探索圆心角、弧、弦之间相等关系的定理,然后加以证明;用推理证明的方法研究圆周角和圆心角的关系;用反证法研究切线的性质;用图形运动的方法认识直线与圆的位置关系,等等.
专题一: 《圆的有关性质》
这一节,先让学生通过实例归纳出圆的定义.根据定义,让学生进一步认识“点与圆的位置关系“和“点到圆心的距离与半径之间的数量关系”的相互联系.本节从集合的观点给出圆的描述性定义,教学时要结合实例使学生体会圆的概念的形成过程。圆既是轴对称图形又是中心对称图形,这一点在前面的学习中,学生已经有所了解.同时,圆还具有旋转不变性.本章借助圆的轴对称性去探索垂径定理;借助圆的旋转不变性去探索圆心角、弧、弦之间的关系.在探索圆周角和圆心角之间的关系的过程中,汪意培养学生的分类讨论思想.确定圆的条件,不仅仅是一个作图问题,
而且可以引发学生对这一类相关问题的数学思考.
专题二:《点和圆、直线和圆的位置关系》
通过直线与圆的相对运动方式,认识直线与圆的位置关系,使学生明
确“直线与圆的位置关系”和“圆心到直线的距离与半径之间的数量关系”的相互联系,体会形与数的统一和转化。教科书还通过切线的性质定理、判定定理、切线长定理和三角形的内切圆概念,重点研究了直线与圆相切的情况,进一步发展学生的推理能力.
专题三:《正多边形和圆》
正多边形是“空间与图形”领域所研究的一类重要的直线形,同时它与最简单的曲线形——圆有着深刻的内在联系.在《正多边形和圆》一节中,不仅让学生探
索它们之间的这种联系,并且学习了几种特殊正多边形的作图方法以及正多边形的边长、边心距和半径的计算问题,为继续学习高中内容做好准备.
专题四:《弧长及扇形的面积》
弧长、扇形的面积、不是直接给出的,而是要求学生进行探索,因此,《弧长及扇形的面积》这节不仅仅要求学生会计算,而且应该使他们理解公式的意义,理解算法的意义.需要说明的是,推理证明是本章采用的研究手段之一,同时,本章还体现了运动、变换转化、分类讨论等数学思想方法,在教学中应注意体现。
五、单元整体规划
起始课(1课时)
整理课(2课时)
探究课(17课时)
圆的有关性质(8课时)
点与圆、直线与圆的位置关系(5课时)
正多边形与圆(2课时)
弧长和扇形面积(2课时)
《圆》大单元教学设计
01
对照课标
03
教学设计
02
教材分析
目录
1
对照课标
1.面向全体学生,注重个体差异,使不同的人在数学上得到相应的发展。
2.课程要反映社会的需要、数学的特点,对内容进行结构化整合,探索发展学生核心素养的路径。
课标分析
3.教学活动是师生积极参与交往互动共同发展的过程,引导学生在真实情境中发现问题和提出问题,逐步形成核心素养。
4.通过学业质量标准的构建,融合 “四基”“四能”和核心素养的主要表现,形成阶段性评价的主要依据。
5.合理利用现代信息技术,创设合理的信息化学习环境,提升学生的探究热情,开阔学生的视野,激发学生的想象力,提高学生的信息素养。
立德树人
结构特征课程
改进教学评价
师生合作
信息资源融合
课程理念
单元总目标
对照《课标》
①理解圆、弧、弦、圆心角、圆周角的概念,了解等圆、等弧的概念;探索并掌握点与圆的位置关系。
②探索并证明垂径定理:垂直于弦的直径平分弦以及弦所对的两条弧。
③探索圆周角与圆心角及其所对弧的关系,知道同弧(或等弧) 所对的圆周角相等。了解并证明圆周角定理及其推论:圆周角等于它 所对弧上的圆心角的一半;直径所对的圆周角是直角,90°的圆周角 所对的弦是直径;圆内接四边形的对角互补。
④了解三角形的内心与外心。
⑤了解直线与圆的位置关系,掌握切线的概念。
⑥能用尺规作图:过不在同一直线上的三点作圆;作三角形的外接圆、内切圆;作圆的内接正方形和内接正六边形。
⑦*能用尺规作图:过圆外一点作圆的切线。
⑧*探索并证明切线长定理:过圆外一点的两条切线长相等。
⑨会计算圆的弧长、扇形的面积。
⑩了解正多边形的概念及正多边形与圆的关系。
2
教材分析
本单元属于图形与几何板块的图形的认识方面的内容。学生在第一学段已经直观地认识了圆,并学习了长方形、正方形等平面图形以及它们的周长、面积计算,在此基础上本单元进一步学习圆的知识,为以后学习圆柱、圆锥等知识和绘制简单扇形统计图打好基础。
本单元学习的圆是一种曲线图形,和以前学的直线图形在性质上有很大的不同,但在研究方法上,联系又很紧密。学生学习这部分知识时,要留给他们充分的思考与探究空间,让学生重点体会“化曲为直”“化圆为方”等转化的数学思想,以及无限逼近的“极限思想”等。
教材分析
主题单元结构分析(纵向)
自然单元内容分析(横向)
3
单元教学设计
字符延长
二
教学重难点
三
学情分析
一
教学思路
四
教学建议
五
单元整体规划
一、单元教学设计思路
圆是平面几何中基本的图形之一,它不仅在几何中有重要地位,而且是进一步学习其他数学知识的重要基础。本章是在小学学过的圆的基础知识上,系统的研究圆的概念、性质、与圆有关的位置关系,正多边形和圆,圆的有关计算及证明。
与“直线形’’图形相比,圆具有独特的对称性。它不仅是轴对称图形,而且是中心对称图形,垂径定理、切线长定理都是圆的对称性的具体表现,可以通过圆的对称性来研究这些内容。
《圆》这一章的教学是初中平面几何中最为复杂的,其中包含了圆自身众多构成要素和相关要素之间的性质,而它的研究方法又和以前研究图形的方法有着相似之处,所以这一章的学习可以借鉴前面研究图形的经验。例如,圆的对称性所产生的性质,参照等腰三角形和平行四边形研究的经验,这样既帮助学生降低了难度,也为他们搭建了探究的平台;圆与其他图形的位置关系的问题之间有相互借鉴价值的,这些都需要在教学过程中加以凸显,让学生在学习过程中体会几何学习的方法。感悟图形研究的途径,从而对今后的数学学习产生深远影响。
二、教学重难点
(1)理解圆、弧、弦、圆心角、圆周角的概念,了解等圆、等弧的概念;掌握点与圆的位置关系。
(2)掌握垂径定理及其推论,并能用垂径定理解决相关问题。
(3)掌握圆周角与圆心角及其所对弧的关系,掌握圆周角定理及其推论。
(4)了解道三角形的内心和外心,掌握内心和外心的位置。
(5)理解直线和圆的位置关系,掌握切线的概念。
(6)掌握切线的判定方法及其性质
(7)掌握切线长定理
(8)了解圆与圆的位置关系。
(9)了解正多边形的概念及正多边形与圆的关系。
(10)会计算圆的弧长、扇形的面积。
三、学情分析
学生在学习本章之前,已通过折叠、对称、平移旋转、推理证明等方式认识了许多图形的性质,积累了大量的空间与图形的经验.本章是在学习了这些直线形的有关性质的基础上,进一步来探索一种特殊的曲线──圆的有关性质,而且把直线形里学过的的一些基本图形,几何变换加以灵活运用.通过本章的学习,学生会对圆有一个较为全面系统的认识,而且对各种数学思想如分类讨论,转化思想,完全归纳、类比的思想等有很好的理解和把握。
四、教学建议
本章是在学习了直线型图形的有关性质和证明的基础上,来探索一种最简单、最常见的曲线型图形——圆的有关性质,在学习这一章之前,学生已经通过折纸、对称、平移、旋转、推理证明等方式认识了许多图形的性质.在本章的设计中,充分利用了学生的已有经验.例如,采用折叠、旋转的方法探索圆的对称性;利用轴对称变换的方法探索垂径定理及其逆定理;用旋转变换的方法探索圆心角、弧、弦之间相等关系的定理,然后加以证明;用推理证明的方法研究圆周角和圆心角的关系;用反证法研究切线的性质;用图形运动的方法认识直线与圆的位置关系,等等.
专题一: 《圆的有关性质》
这一节,先让学生通过实例归纳出圆的定义.根据定义,让学生进一步认识“点与圆的位置关系“和“点到圆心的距离与半径之间的数量关系”的相互联系.本节从集合的观点给出圆的描述性定义,教学时要结合实例使学生体会圆的概念的形成过程。圆既是轴对称图形又是中心对称图形,这一点在前面的学习中,学生已经有所了解.同时,圆还具有旋转不变性.本章借助圆的轴对称性去探索垂径定理;借助圆的旋转不变性去探索圆心角、弧、弦之间的关系.在探索圆周角和圆心角之间的关系的过程中,汪意培养学生的分类讨论思想.确定圆的条件,不仅仅是一个作图问题,
而且可以引发学生对这一类相关问题的数学思考.
专题二:《点和圆、直线和圆的位置关系》
通过直线与圆的相对运动方式,认识直线与圆的位置关系,使学生明
确“直线与圆的位置关系”和“圆心到直线的距离与半径之间的数量关系”的相互联系,体会形与数的统一和转化。教科书还通过切线的性质定理、判定定理、切线长定理和三角形的内切圆概念,重点研究了直线与圆相切的情况,进一步发展学生的推理能力.
专题三:《正多边形和圆》
正多边形是“空间与图形”领域所研究的一类重要的直线形,同时它与最简单的曲线形——圆有着深刻的内在联系.在《正多边形和圆》一节中,不仅让学生探
索它们之间的这种联系,并且学习了几种特殊正多边形的作图方法以及正多边形的边长、边心距和半径的计算问题,为继续学习高中内容做好准备.
专题四:《弧长及扇形的面积》
弧长、扇形的面积、不是直接给出的,而是要求学生进行探索,因此,《弧长及扇形的面积》这节不仅仅要求学生会计算,而且应该使他们理解公式的意义,理解算法的意义.需要说明的是,推理证明是本章采用的研究手段之一,同时,本章还体现了运动、变换转化、分类讨论等数学思想方法,在教学中应注意体现。
五、单元整体规划
起始课(1课时)
整理课(2课时)
探究课(17课时)
圆的有关性质(8课时)
点与圆、直线与圆的位置关系(5课时)
正多边形与圆(2课时)
弧长和扇形面积(2课时)
