【大单元教学】鲁教版2023年九年级大单元教学 第一章反比例函数综合题课件(14张PPT)
文档属性
| 名称 | 【大单元教学】鲁教版2023年九年级大单元教学 第一章反比例函数综合题课件(14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 763.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 10:08:52 | ||
图片预览






文档简介
(共14张PPT)
反比例函数综合题
新课标内容要求
结合具体情境体会反比例函数的意义,能根据已 知条件确定反比例函数的表达式
能画反比例函数的图像,根据图像和表达式 y=(k≠0)探索并理解k>0和k<0时图像的变化情况。
能用反比例函数解决简单实际问题。
反比例函数
概念:形如y=(k为常数k≠0)
题型
哪些是反比例函数
求字母的值
y=
y=k
xy=k
(k为常数k≠0)
指数-1
系数≠0
图形与性质
K>0
K<0
o
y
x
一、三象限
o
y
x
二、四象限
题型:与一次函数、二次函数结合
解析式
待定系数法
面积法(K)的几何意义
应用
题型:
1、代入一组x、y的对应值或图像上一点坐标求出K值
2、与一次函数结合、求解析式
矩形面积=|k|
三角形面积=
| |
与三角形、平行四边形结合
1、交点问题
2、不等式的范围
步骤:1、求解析式
2、求交点
3、谁在上面谁大
4、写范围(在交点同一侧)
3、面积有关计算
对称性 关于原点成中心对称、关于y=±x成轴对称
4、特殊三角形存在问题
题型:与一次函数结合
在实际生活中的应用
概念:
例题:
1.下列关系式中,哪个等式表示y是x的反比例函数( )
A. B. C. D.
2.下列关系式中的两个量成反比例的是( )
A.圆的面积与它的半径;
B.正方形的周长与它的边长;
C.路程一定时,速度与时间;
D.长方形一条边确定时,周长与另一边.
3.已知函数y=(m-2)
是反比例函数,则m的值为( )
A.2 B.-2 C.2或-2 D.任意实数
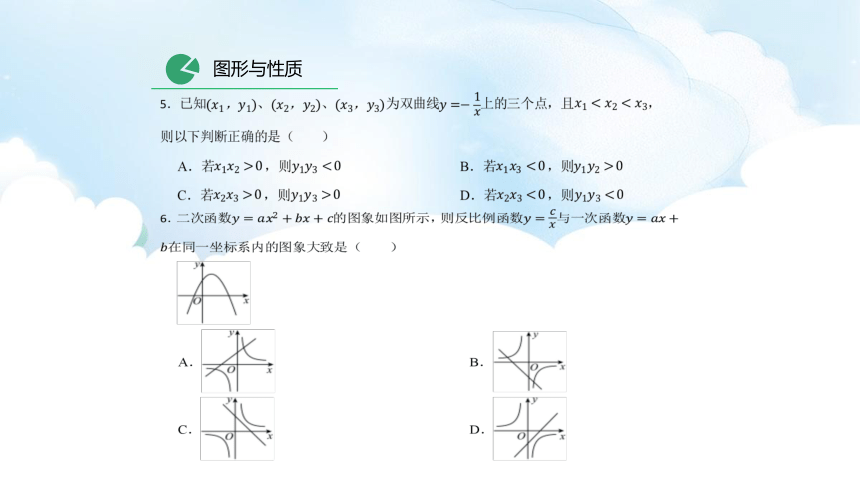
图形与性质
图形与性质
9.如图,在平面直角坐标系中,函数 y=kx 与 y=的图象交于 A、B 两点,过 A 作 y
轴的垂线,交函数的图象于点 C,连接 BC,则△ABC 的面积为( )
A.2 B.4 C.6 D.8
解析式
10.已知点(-2,1)在双曲线 上,则k的值为( )
A.2 B.0 C.1 D.-2
解析式
应用
应用
应用
应用
应用
谢谢大家!
反比例函数综合题
新课标内容要求
结合具体情境体会反比例函数的意义,能根据已 知条件确定反比例函数的表达式
能画反比例函数的图像,根据图像和表达式 y=(k≠0)探索并理解k>0和k<0时图像的变化情况。
能用反比例函数解决简单实际问题。
反比例函数
概念:形如y=(k为常数k≠0)
题型
哪些是反比例函数
求字母的值
y=
y=k
xy=k
(k为常数k≠0)
指数-1
系数≠0
图形与性质
K>0
K<0
o
y
x
一、三象限
o
y
x
二、四象限
题型:与一次函数、二次函数结合
解析式
待定系数法
面积法(K)的几何意义
应用
题型:
1、代入一组x、y的对应值或图像上一点坐标求出K值
2、与一次函数结合、求解析式
矩形面积=|k|
三角形面积=
| |
与三角形、平行四边形结合
1、交点问题
2、不等式的范围
步骤:1、求解析式
2、求交点
3、谁在上面谁大
4、写范围(在交点同一侧)
3、面积有关计算
对称性 关于原点成中心对称、关于y=±x成轴对称
4、特殊三角形存在问题
题型:与一次函数结合
在实际生活中的应用
概念:
例题:
1.下列关系式中,哪个等式表示y是x的反比例函数( )
A. B. C. D.
2.下列关系式中的两个量成反比例的是( )
A.圆的面积与它的半径;
B.正方形的周长与它的边长;
C.路程一定时,速度与时间;
D.长方形一条边确定时,周长与另一边.
3.已知函数y=(m-2)
是反比例函数,则m的值为( )
A.2 B.-2 C.2或-2 D.任意实数
图形与性质
图形与性质
9.如图,在平面直角坐标系中,函数 y=kx 与 y=的图象交于 A、B 两点,过 A 作 y
轴的垂线,交函数的图象于点 C,连接 BC,则△ABC 的面积为( )
A.2 B.4 C.6 D.8
解析式
10.已知点(-2,1)在双曲线 上,则k的值为( )
A.2 B.0 C.1 D.-2
解析式
应用
应用
应用
应用
应用
谢谢大家!
