【大单元教学】鲁教版2023年九年级大单元教学 第一章反比例综合题 课件(20张PPT)
文档属性
| 名称 | 【大单元教学】鲁教版2023年九年级大单元教学 第一章反比例综合题 课件(20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
反比例函数综合题
1、知识目标:
(1)一次函数、正比例函数、反比例函数的概念。
(2)一次函数、正比例函数、反比例函数的图象及性质。
2、能力目标:
(1)用待定系数法求一次函数、正比例函数、反比例函数的解析式。
(2)会用作出一次函数、正比例函数、反比例函数的图象。
(3)能够应用一次函数与反比例函数的图象与性质分析解决一次函数与反比例函数的综合题。
三、教学重点:
1.一次函数、正比例函数、反比例函数的图象及性质。
2.用待定系数法求一次函数、正比例函数、反比例函数的解析式。
3.熟练应用一次函数与反比例函数的图象与性质进行解题。
四、教学难点:
1.灵活运用一次函数、正比例函数、反比例函数的有关知识解综合题。
2.进一步利用数形结合的思想方法进行解题。
五、教学方法:讲练结合
六、学情分析:
学生已经基本掌握反比例函数和一次函数的概念、图象和性质,但我校学生计算能力、试图能力和分析能力都有待提高,因此我选择了稍微简单的综合题,意在让学生提高能力的同时增强学习数学的自信心。
一、一次函数与反比例函数综合图象判断
方法1、分类讨论 k、b的符号;
方法2、四个图逐个分析判断;
方法3、运用特殊点(值)去排除(此种方法作参考,不能完全排三选一)
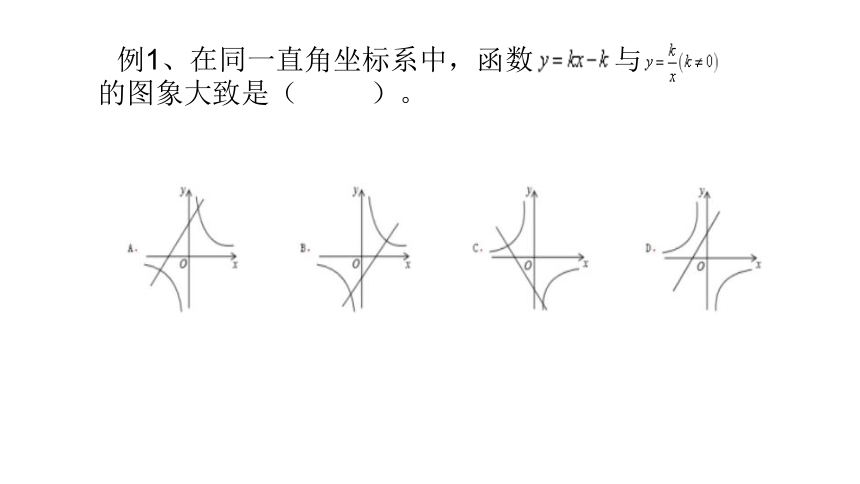
例1、在同一直角坐标系中,函数 与 的图象大致是( )。
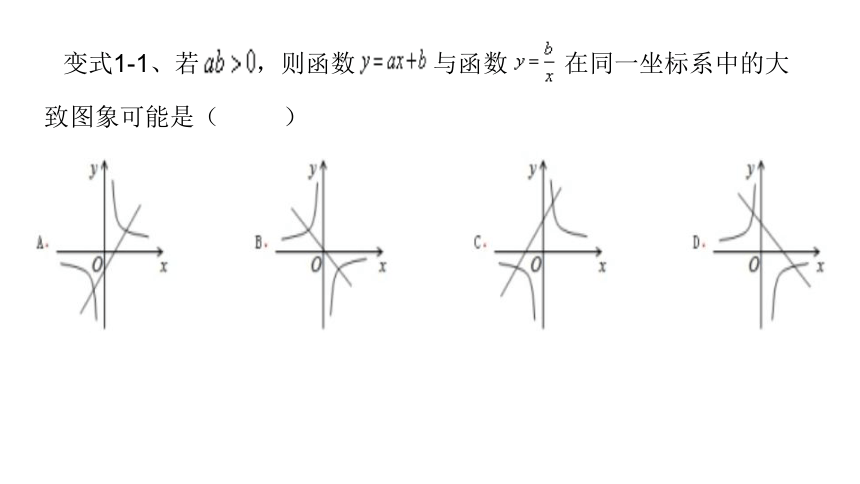
变式1-1、若 ,则函数 与函数 在同一坐标系中的大致图象可能是( )
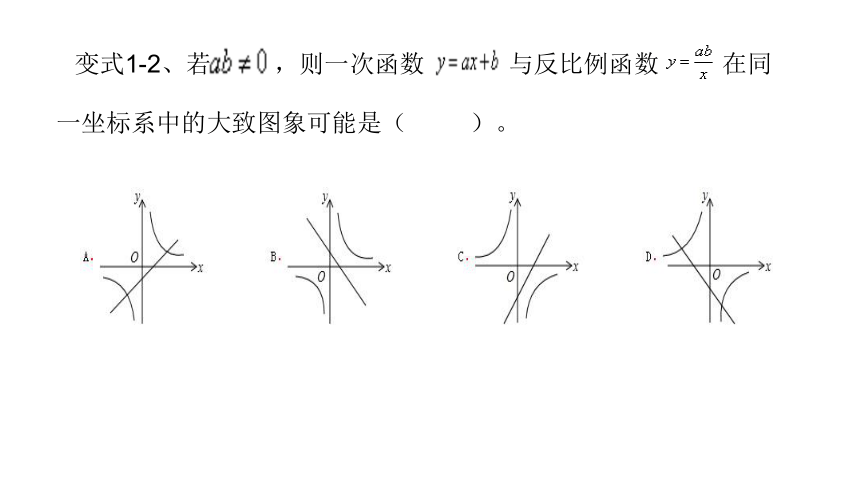
变式1-2、若 ,则一次函数 与反比例函数 在同一坐标系中的大致图象可能是( )。
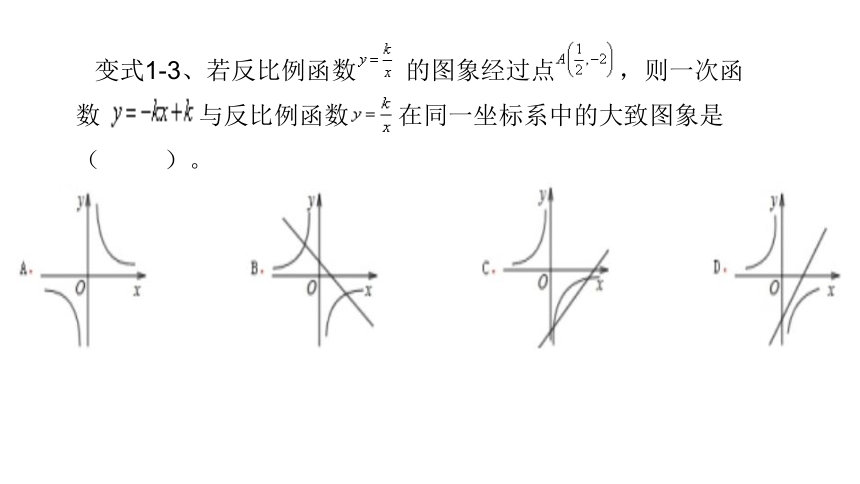
变式1-3、若反比例函数 的图象经过点 ,则一次函数 与反比例函数 在同一坐标系中的大致图象是( )。
二、一次函数与反比例函数综合题的解题思路
①先求反比例函数解析式,再求一次函数解析式;
②联立方程组求交点坐标;
③将交点坐标带入解析式求待定系数的值;
④判断两个函数值之间的大小时自变量的取值范围直接看图得出;
⑤求不规则三角形(此处的不规则指三角形三边均不与坐标轴平行或重合)的面积采用分割法(通常是选取与坐标轴的交点分割成两个同底三角形)。
例2、如图,反比例函数的图象与一次函数图象交于 。
(1)求一次函数和反比例函数的解析式;
(2)求 的面积;
(3)直接写出一次函数的值大于反比例函数值得自变量x的取值范围。
变式2-1、如图,已知反比例函数 与一次函数 的图象在第一象限相交于 。
(1)试确定这两个函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标,并根据图象写出使反比例函数的值大于一次函数的值的x的取值范围。
变式2-2、如图,反比例函数 与一次函数 的图象交于A、B两点。
(1)求A、B两点的坐标。
(2)求 的面积;
(3)根据图象直接写出使一次函数的值大于反比例函数的值的 的取值范围。
变式2-3、如图,一次函数 的图象与x轴交于点A,与
轴交于点B,与反比例函数 图象的一个交点为 。
(1)求反比例函数的解析式;
(2)当 时,求 的取值范围;
(3)求点B到直线OM的距离。
变式2-4 如图,在平面直角坐标系中,一次函数 和 的图象相交于点A,反比例函数 的图象经过点A .
(1)求反比例函数的表达式;
(2)设一次函数 的图象与反比例函数 的图象的另一个交点为B,连接OB,求△ABO的面积.
三、两线段和的最小值(或差绝对值的最大值)
通过对称将两条线段转移到一条直线上,通过两点之间线段最短来完成。
例3、已知正比例函数 的图象与反比例函数 在第一象限内的图象交于点A,过点A作X轴的垂线,垂足为点P,已知△OAP的面积为1.
(1)求反比例函数的解析式;
(2)有一点的横坐标为2,且在反比例函数
图象上,则在X轴上是否存在一点,使得
MA+MB最小?若存在,请求出点M的坐标;若不存在,请说明理由。
变式3-1 如图,点 是一次函数 的
图象和反比例函数 的图象的两个交点。
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于
反比例函数的值的X的取值范围;
(3)若C是x轴上一动点,设 ,求t的最大值,
并求出此时点C的坐标。
四、存在性问题
例4、如图,反比例函数 的图象与一次函数 的
图象交于点A、B,点A、B的横坐标分别为1、-2,一次函数图
象与y轴交于点C,与x轴交于点D。
(1)求一次函数的解析式;
(2)对于反比例函数 ,当y<-1时,写出x的取值范围;
(3)在第三象限的反比例函数图象上是否存在一点P,使
得 ?若存在,请求出点P的坐标;若不存在,请说明理由。
变式4-1、如图,一次函数 的图象与
反比例函数 的图象交于点P(n,2),与
x轴交于点A(-4,0),与y轴交于点C,PB⊥x轴于
点B,且AC=BC。
(1)求一次函数、反比例函数的解析式;
(2)反比例函数图象上是否存在点D,使
四边形BCPD为菱形?如果存在,求出点D的坐标;
如果不存在,说明理由。
变式4-2、如图,直线 与x 轴交于点C(4,0),
与y轴交于点B,并与双曲线 交于点A(-1,n)。
(1)求直线与双曲线的解析式;
(2)连接OA,求∠OAB的正弦值;
(3)若点D在x轴的正半轴上,是否存在
以点D、C、B构成的三角形与△OAB相似?
若存在求出点D的坐标,若不存在,请说明理由。
反比例函数综合题
1、知识目标:
(1)一次函数、正比例函数、反比例函数的概念。
(2)一次函数、正比例函数、反比例函数的图象及性质。
2、能力目标:
(1)用待定系数法求一次函数、正比例函数、反比例函数的解析式。
(2)会用作出一次函数、正比例函数、反比例函数的图象。
(3)能够应用一次函数与反比例函数的图象与性质分析解决一次函数与反比例函数的综合题。
三、教学重点:
1.一次函数、正比例函数、反比例函数的图象及性质。
2.用待定系数法求一次函数、正比例函数、反比例函数的解析式。
3.熟练应用一次函数与反比例函数的图象与性质进行解题。
四、教学难点:
1.灵活运用一次函数、正比例函数、反比例函数的有关知识解综合题。
2.进一步利用数形结合的思想方法进行解题。
五、教学方法:讲练结合
六、学情分析:
学生已经基本掌握反比例函数和一次函数的概念、图象和性质,但我校学生计算能力、试图能力和分析能力都有待提高,因此我选择了稍微简单的综合题,意在让学生提高能力的同时增强学习数学的自信心。
一、一次函数与反比例函数综合图象判断
方法1、分类讨论 k、b的符号;
方法2、四个图逐个分析判断;
方法3、运用特殊点(值)去排除(此种方法作参考,不能完全排三选一)
例1、在同一直角坐标系中,函数 与 的图象大致是( )。
变式1-1、若 ,则函数 与函数 在同一坐标系中的大致图象可能是( )
变式1-2、若 ,则一次函数 与反比例函数 在同一坐标系中的大致图象可能是( )。
变式1-3、若反比例函数 的图象经过点 ,则一次函数 与反比例函数 在同一坐标系中的大致图象是( )。
二、一次函数与反比例函数综合题的解题思路
①先求反比例函数解析式,再求一次函数解析式;
②联立方程组求交点坐标;
③将交点坐标带入解析式求待定系数的值;
④判断两个函数值之间的大小时自变量的取值范围直接看图得出;
⑤求不规则三角形(此处的不规则指三角形三边均不与坐标轴平行或重合)的面积采用分割法(通常是选取与坐标轴的交点分割成两个同底三角形)。
例2、如图,反比例函数的图象与一次函数图象交于 。
(1)求一次函数和反比例函数的解析式;
(2)求 的面积;
(3)直接写出一次函数的值大于反比例函数值得自变量x的取值范围。
变式2-1、如图,已知反比例函数 与一次函数 的图象在第一象限相交于 。
(1)试确定这两个函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标,并根据图象写出使反比例函数的值大于一次函数的值的x的取值范围。
变式2-2、如图,反比例函数 与一次函数 的图象交于A、B两点。
(1)求A、B两点的坐标。
(2)求 的面积;
(3)根据图象直接写出使一次函数的值大于反比例函数的值的 的取值范围。
变式2-3、如图,一次函数 的图象与x轴交于点A,与
轴交于点B,与反比例函数 图象的一个交点为 。
(1)求反比例函数的解析式;
(2)当 时,求 的取值范围;
(3)求点B到直线OM的距离。
变式2-4 如图,在平面直角坐标系中,一次函数 和 的图象相交于点A,反比例函数 的图象经过点A .
(1)求反比例函数的表达式;
(2)设一次函数 的图象与反比例函数 的图象的另一个交点为B,连接OB,求△ABO的面积.
三、两线段和的最小值(或差绝对值的最大值)
通过对称将两条线段转移到一条直线上,通过两点之间线段最短来完成。
例3、已知正比例函数 的图象与反比例函数 在第一象限内的图象交于点A,过点A作X轴的垂线,垂足为点P,已知△OAP的面积为1.
(1)求反比例函数的解析式;
(2)有一点的横坐标为2,且在反比例函数
图象上,则在X轴上是否存在一点,使得
MA+MB最小?若存在,请求出点M的坐标;若不存在,请说明理由。
变式3-1 如图,点 是一次函数 的
图象和反比例函数 的图象的两个交点。
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于
反比例函数的值的X的取值范围;
(3)若C是x轴上一动点,设 ,求t的最大值,
并求出此时点C的坐标。
四、存在性问题
例4、如图,反比例函数 的图象与一次函数 的
图象交于点A、B,点A、B的横坐标分别为1、-2,一次函数图
象与y轴交于点C,与x轴交于点D。
(1)求一次函数的解析式;
(2)对于反比例函数 ,当y<-1时,写出x的取值范围;
(3)在第三象限的反比例函数图象上是否存在一点P,使
得 ?若存在,请求出点P的坐标;若不存在,请说明理由。
变式4-1、如图,一次函数 的图象与
反比例函数 的图象交于点P(n,2),与
x轴交于点A(-4,0),与y轴交于点C,PB⊥x轴于
点B,且AC=BC。
(1)求一次函数、反比例函数的解析式;
(2)反比例函数图象上是否存在点D,使
四边形BCPD为菱形?如果存在,求出点D的坐标;
如果不存在,说明理由。
变式4-2、如图,直线 与x 轴交于点C(4,0),
与y轴交于点B,并与双曲线 交于点A(-1,n)。
(1)求直线与双曲线的解析式;
(2)连接OA,求∠OAB的正弦值;
(3)若点D在x轴的正半轴上,是否存在
以点D、C、B构成的三角形与△OAB相似?
若存在求出点D的坐标,若不存在,请说明理由。
