【大单元教学】鲁教版2023年九年级大单元教学 几何综合题 课件(83张PPT)
文档属性
| 名称 | 【大单元教学】鲁教版2023年九年级大单元教学 几何综合题 课件(83张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 16.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 00:00:00 | ||
图片预览










文档简介
(共83张PPT)
鲁教版中考数学复习
几何综合题
鲁教版五四制初中数学
几何综合题在中考中的地位:
对于中考数学,几何是永远绕不开的话题,往大方向说,谁吃透几何,谁就能占领中考的高分地,至少分数上肯定不会差。几何部分部分即是中考的重点,也是中考的难点,它包括全等、相似、计算以及添加辅助线等方方面面,是考题的重要组成部分,是考察综合能力的方式方法,正是由于这种综合性的特点,决定了相似三角形在中考中的重要地位。
整 体 结 构
几何综合题单元主要涉及到三角形,四边形和圆三大模块。1,三角形主要包括等腰三角形、等边三角形、直角三角形和一般三角形的全等和相似的证明。2,四边形主要包括平行四边形、菱形、矩形和正方形的判定和性质以及相关计算.3圆主要包括圆的有关概念和性质、圆的有关角和定理的应用和计算。
一:掌握相关图形的性质和判定定理
二:详细讲解几何相关例题
三:讲解与例题相关几何模型
四:小组合作解决问题
五:独立解决相关模型问题
主题问题单元设计
专题划分
三角形
课内8课时
课外3课时
四边形
课内12课时
课外4课时
圆
课内5课时
课外4课时
三角形
(1)理解三角形及其内角、外角、中线、高线、角平分线等概念,了解三角形的稳定性,探索并证明三角形的内角和定理.掌握它的推论。
(2)理解全等三角形的概念,能识别全等三角形中的对应边、对应角并能证明三角形全等。
(3)探索并证明角平分线的性质定理和线段垂直平分线的性质定理。
(4)了解等腰三角形和等边三角形的概念,探索并证明等腰三角形和等边三角形的性质定理和判定定理以及三线合一。
(5)了解直角三角形的概念探索并掌握直角三角形的性质定理和判定定理,直角三角形斜边上的中线等于斜边的一半,探索勾股定理及其逆定理,探索并掌握判定直角三角形全等的“斜边、直角边”定理。
符合新课标的单元教学目标
三角形专题
三角形
目标
1,掌握三角形相关基础知识(2课时)
2,掌握三角形有关模型的全等或相似证明(3课时)
3,完成三角形有关模型的全等或相似证明(3课时)
模型
手拉手模型
三垂直模型
相似模型
三角形有关的知识
【考点总结】一、三角形中的重要线段
1.三角形的高线:从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称高.
特性:三角形的三条高线相交于一点.
2.三角形的中线:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.特性:三角形的三条中线交于一点.
3.三角形的中位线:连接三角形两边中点的线段叫做三角形的中位线.
定理:三角形的中位线平行于第三边,且等于它的一半
4.三角形的角平分线:三角形一个角的平分线和这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.
特性:三角形的三条角平分线交于一点,这点叫做三角形的内心.
性质:角平分线上的点到角的两边的距离相等.
判定:角的内部到角的两边距离相等的点在角的平分线上,角的平分线可以看作是到角两边距离相等的点的集合.
5.线段垂直平分线:经过线段中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫中垂线.
性质:线段垂直平分线上的点到这条线段两个端点的距离相等.
判定:到一条线段的两个端点距离相等的点在线段的垂直平分线上,线段的垂直平分线可以看作是到线段两端点距离相等的点的集合.
【考点总结】二、等腰三角形及等边三角形的性质与判定
1.等腰三角形的有关概念及分类:有两边相等的三角形叫等腰三角形,三边相等的三角形叫做等边三角形,也叫正三角形;等腰三角形分为腰和底不相等的等
2.等腰三角形的性质:
(1)等腰三角形的两个底角相等(简称为“等边对等角”);
(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称为“三线合一”);
(3)等腰三角形是轴对称图形.
3.等腰三角形的判定:如果一个三角形有两个角相等,那么这两个角所对的边也相等.
4.等边三角形的性质:
(1)等边三角形的内角相等,且都等于60°;(2)等边三角形的三条边都相等.
5.等边三角形的判定:
(1)三条边相等的三角形是等边三角形;(2)三个角相等的三角形是等边三角形;
(3)有一个角为60°的等腰三角形是等边三角形.
【考点总结】三、直角三角形的有关性质和判定
1.直角三角形的有关性质
(1).直角三角形的两锐角互余.(2).直角三角形中,30°角所对的边等于斜边的一半.(3).直角三角形斜边上的中线等于斜边的一半.(4).勾股定理:直角三角形两直角边的平方和等于斜边的平方.
2.直角三角形的判定
(1).有一个角等于90°的三角形是直角三角形.(2).有两角互余的三角形是直角三角形.(3).如果三角形一边上的中线等于这边的一半,则该三角形是直角三角形.(4).勾股定理的逆定理:如果三角形一条边的平方等于另外两条边的平方和,那么这个三角形是直角三角形.
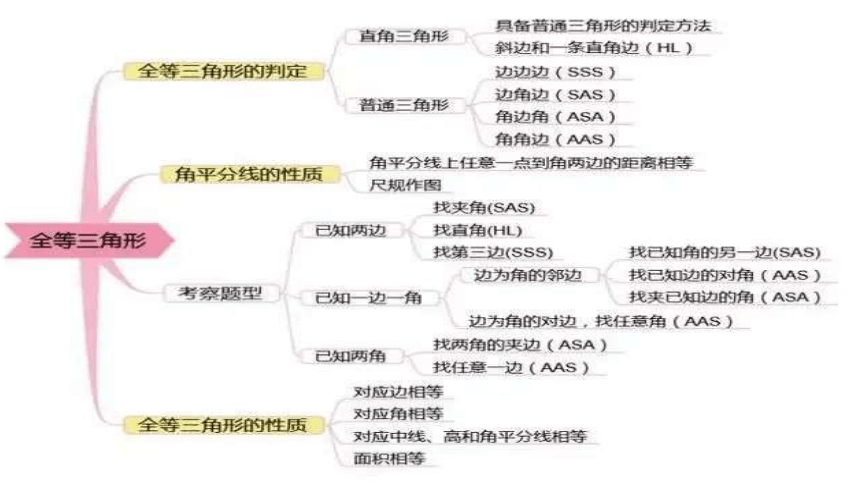
【考点总结】四、全等三角形的性质与判定
1.概念:能够完全重合的两个三角形叫做全等三角形.
2.性质:全等三角形的对应边、对应角分别相等.
3.判定:(1)有三边对应相等的两个三角形全等,简记为(SSS);
(2)有两边和它们的夹角对应相等的两个三角形全等,简记为(SAS);
(3)有两角和它们的夹边对应相等的两个三角形全等,简记为(ASA);
(4)有两角和其中一角的对边对应相等的两个三角形全等,简记为(AAS);
(5)有斜边和一条直角边对应相等的两个直角三角形全等,简记为(HL).
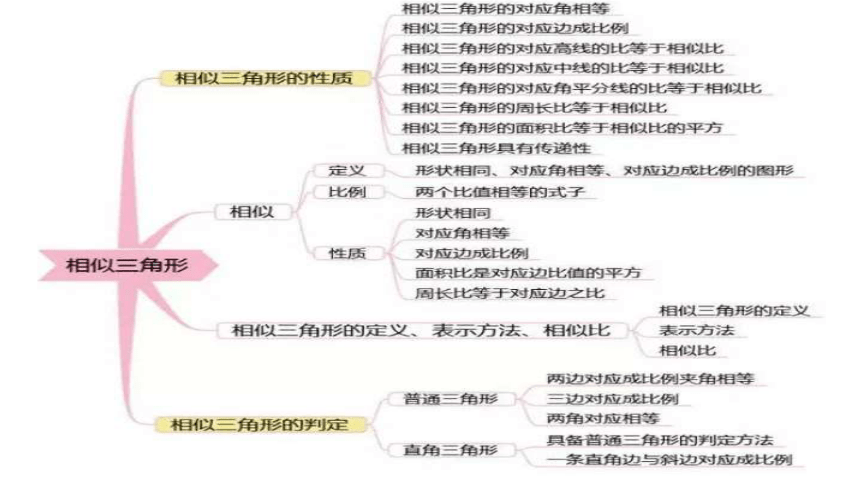
【考点总结】五、相似三角形
1.定义:
各角对应相等,各边对应成比例的两个三角形叫做相似三角形.
2.判定:
(1)平行于三角形一边的直线和其他两边(或两边延长线)相交,所构成的三角形与原三角形相似;
(2)两角对应相等,两三角形相似;
(3)两边对应成比例且夹角相等,两三角形相似;
(4)三边对应成比例,两三角形相似;
(5)斜边和一条直角边对应成比例,两直角三角形相似.
3.性质:
(1)相似三角形的对应角相等,对应边成比例;
(2)相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比;
(3)相似三角形周长的比等于相似比;
(4)相似三角形面积的比等于相似比的平方
例1.图1、图2中,点B为线段AE上一点,△ABC与△BED都是等边三角形。
(1)如图1,求证:AD=CE;
(2)如图2,设CE与AD交于点F,连接BF.
①求证:∠CFA=600;
②求证:CF+BF=AF.
典例讲解
在初中数学里,我们把两个有公共顶点且顶角相等的等腰三角形组成的图形叫手拉手模型。如下图①、图②、图③
手拉手模型
1.在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.
(1)如图1,点M,N分别在AD,AB上,且∠BMN=90°,当∠AMN=30°,AB=2时,求线段AM的长;
(2)如图2,点E,F分别在AB,AC上,且∠EDF=90°,求证:BE=AF;
(3)如图3,点M在AD的延长线上,点N在AC上,且∠BMN=90°,求证:AB+AN
AM.
小组合作
小组合作
2.如图,在等边三角形ABC中,点E是边AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.
【问题解决】
如图1,若点D在边BC上,求证:CE+CF=CD;
【类比探究】
如图2,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.
小组合作
3.【问题探究】
(1)如图1,△ABC和△DEC均为等腰直角三角形,∠ACB=∠DCE=90°,点B,D,E在同一直线上,连接AD,BD.点H.连接HF,AF,其中AF交EC于点M.
①请探究AD与BD之间的位置关系: ;
②若AC=BC=
,DC=CE=
,则线段AD的长为 ;
【拓展延伸】
(2)如图2,△ABC和△DEC均为直角三角形,∠ACB=∠DCE=90°,AC=
,BC=
,CD=
CE=1.将△DCE绕点C在平面内顺时针旋转,设旋转角∠BCD为α(0°≤α<360°),作直线BD,连接AD,当点B,D,E在同一直线上时,画出图形,并求线段AD的长.
手拉手模型分类
关于全等的手拉手模型有①②③④四类
①有公共顶点的等边三角形手拉手
②有公共顶点的等腰直角三角形手拉手
③共顶点且顶角相等的等腰三角形手拉手
④有公共顶点的正方形手拉手
关于相似的手拉手模型有⑤⑥两类
⑤有公共顶点的直角三角形手拉手
⑥有公共顶点的任意三角形手拉手
模型口诀:
等腰共顶手拉手,旋转全等马上有;
左手拉左手,右手拉右手,
两根拉线抖一抖,它们相等不用愁;
拉线夹角与顶角,相等互补答案有。
4.如图,△ABC中,∠BAC=90°,AB=AC,点D在直线BC上,△ADE是等腰直角三角形,∠DAE=90°,AD=AE,连接CE.
(1)当点D在线段BC上时,如图1,求证:DC+CE= AC;
(2)当点D在线段CB延长线上时,如图2,求证: AC=CD-CE
(3)当点D在线段BC延长线上时(如图3),探究线段DC、CE、AC之间的数量关系,并证明.
独立完成
5.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.
独立完成
6.已知△ABC 中,∠BAC=60°,以 AB 和 BC 为边向外作等边△ABD 和等边△BCE.
(1) 连接 AE、CD,如图 1,求证:AE=CD;
(2) 若 N 为 CD 中点,连接 AN,如图 2,求证:CE=2AN;
(3) 若 AB⊥BC,延长 AB 交 DE 于 M,DB=, 如图 3,则 BM= .(直接写出结果)
独立完成
典例讲解
例2如图,在Rt△ABC中,∠ABC=90°点D在BC的延长线上,且BD=AB.过点B作BE⊥AC,与BD的垂线DE交于点E.
(1)求证:△ABC≌△BDE;
(2)请找出线段AB、DE、CD之间的数量关系,并说明理由.
模型描述:
如图,已知△ABC是直角三角形,
∠BAC=90°,AC=BC,直线
l经过点C,分别从点B,A向直
线l作垂线,垂足分别为点D,E.
请证明:△ACD≌△CBE.
模型图例:
三垂直模型
1.在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.
(1)如图1,请直接写出线段OE与OF的数量关系和位置关系;
(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由;
(3)若|CF-AE|=2,EF=2,当△POF为等腰三角形时,请直接写出线段OP的长.
小组合作
例3在△ABC中,AD平分∠BAC交BC于点D,F为AD上一点,且BF=BD.BF的延长线交AC于点E.
(1)求证:AB AD=AF AC;
(2)若∠BAC=60°.AB=4,AC=6, 求DF的长;
典例讲解
相似模型
平行线型
斜交型
子母型
一线三等角型
小组合作
1.如图,△ABC中,∠ACB=90°,CB=CA,CE⊥AB于E,点F是CE上一点,连接AF并延长交BC于点D,CG⊥AD于点G,连接EG.
(1)求证:△DCG∽△DAC;
(2)如图1,若CF=2EF,求证:点D是BC中点;
(3)如图2,若GC=4,GE=4 ,求GD.
独立完成
2.已知:如图,在△ABC中,点D在边BC上,AE∥BC,BE与AD、AC分别相交于点F、G,
(1)求证:△CAD∽△CBG;
(2)连接DG,求证:
(3)若AB=AC=9,BC=6,点D是BC的中点,连接CE,求CE的长.
四边形
(1)了解多边形的定义,多边形的顶点、边、内角、外角、对角线等概念;探索并掌握多边形内角和与外角和公式.
(2)理解平行四边形、矩形、菱形、正方形的概念,以及它们之间的关系;了解四边形的不稳定性.
(3)探索并证明平行四边形的性质定理和判定定理
(4)了解两条平行线之间距离的意义,能度量两条平行线之间的距离.
(5)探索并证明矩形、菱形、正方形的性质定理和判定定理
符合新课标的单元教学目标
四边形专题
四边形
目标
1,掌握四边形相关基础知识(2课时)
2,掌握四边形有关模型的全等或相似证明(5课时)
3,完成四边形形有关模型的全等或相似证明(5课时)
模型
中 点 模 型
角平分线模型
半 角 模 型
旋 转 模 型
相似及其他模型
【考点总结】一、多边形的有关概念及性质
1.多边形的概念
定义:在平面内,由一些不在同一直线上的线段首尾顺次相接组成的图形叫做多边形.
对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
正多边形:各个角都相等,各条边都相等的多边形叫做正多边形.
2.性质:n边形的内角和为(n-2)·180°,外角和为360°.
【考点总结】二、平行四边形的定义和性质
1.定义:两组对边分别平行的四边形叫做平行四边形.
2.性质:
(1)平行四边形的对边相等且平行.
(2)平行四边形的对角相等.
(3)平行四边形的对角线互相平分.
(4)平行四边形是中心对称图形.
【考点总结】三、平行四边形的判定
1.两组对边分别相等的四边形是平行四边形.
2.两组对边分别平行的四边形是平行四边形.
3.一组对边平行且相等的四边形是平行四边形.
4.对角线相互平分的四边形是平行四边形.
5.两组对角分别相等的四边形是平行四边形.
四边形有关知识
【考点总结】四、矩形的性质与判定
1.定义:有一个角是直角的平行四边形是矩形.
2.性质:
(1)矩形的四个角都是直角.
(2)矩形的对角线相等.
(3)矩形既是轴对称图形,又是中心对称图形,它有两条对称轴;它的对称中心是对角线的交点.
3.判定:
(1)有三个角是直角的四边形是矩形.
(2)对角线相等的平行四边形是矩形.
(3)有一个角是直角的平行四边形是矩形.
【考点总结】五、菱形的性质与判定
1.定义:一组邻边相等的平行四边形叫做菱形.
2.性质:
(1)菱形的四条边都相等.
(2)菱形的对角线互相垂直且平分,并且每一条对角线平分一组对角.
3.判定:
(1)对角线互相垂直的平行四边形是菱形.
(2)四条边都相等的四边形是菱形.
(3)一组邻边相等的平行四边形叫做菱形.
【考点总结】六、正方形的性质与判定
1.定义:一组邻边相等的矩形叫做正方形.
2.性质:
(1)正方形的四条边都相等,四个角都是直角.
(2)正方形的对角线相等,且互相垂直平分;每条对角线平分一组对角.
(3)正方形是轴对称图形,两条对角线所在直线,以及过每一组对边中点的直线都是它的对称轴;正方形是中心对称图形,对角线的交点是它的对称中心.21世纪教育网版权所有
3.判定:
(1)一组邻边相等并且有一个角是直角的平行四边形是正方形.
(2)一组邻边相等的矩形是正方形.
(3)对角线互相垂直的矩形是正方形.
(4)有一个角是直角的菱形是正方形.
例4如图,△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点, FG⊥BC于点G,与DE交于点H,若FG=AF, AG平分∠BAC,连接GE, ;GD.
(1)求证:△ECG≌△GHD
(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论.
(3)若∠B=300,判定四边形AEGF是否为菱形,并说明理由.
1、倍长中线:遇到线段的中点问题,常借助倍长中线的方法还原中心对称图形,利用“8”字形全等将题中条件集中,达到解题的目的,这种方法是最常用的也是最重要的方法, 在△ABC中,M为BC边的中点:
(1)如图1,连结AM并延长至点F,使得ME=AM,连结CE.则△ABM≌△ECM;
(2)如图2,点D在AB边上,连结DM并延长至点E,使得ME=DM,连结CE,则△BDM≌△CEM。
中点模型
2、构造中位线:三角形的中位线从位置关系和数量关系两方面将将图形中分散的线段关系集中起来,通常需要再找一个中点来构造中位线,或者倍长某线段构造中位线,在△ABC中,D为AB边的中点,则:
(1)如图1,取AC边的中点E,连结DE,则DE//BC,且DF=0.5BC.
(2)如图2,延长BC至点F,使得CF=BC,连结CD,AF,则DC//AF,且DC=0.5AE。
3、等腰三角形“三线合一”。如图,在△ABC中,若AB=AC;通常取底边BC的中点D,则AD⊥BC,且AD平分∠BAC。事实上,在△ABC中:①AB=AC;②AD平分∠BAC;③BD=CD,④AD⊥BC;对于以上四条语句,任意选择两个作为条件,就可以推出另两条结论,即“知二得二”。
4、直角三角形斜边中线。如图,在△ABC看,∠ABC=900,取AC的中点D,连结BD,则有BD=AD=CD=AC;反过来,在△ABC中,点D在AC边上,若BD=AD=CD=0.5AC,则有∠ABC=90°。
1.已知两个等腰Rt△ABC,Rt△CEF有公共顶点C,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;
(2)如图2,当∠BCE=45°时,求证:BM=ME.
小组合作
小组合作
2.如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.
(1)若ED⊥EF,求证:ED=EF;
(2)在(1)的条件下,若DC的延长线与FB交于点P,试判定四边形ACPE是否为平行四边形 并证明你的结论(请先补全图形,再解答);
(3)若ED=EF,ED与EF垂直吗 若垂直给出证明.
小组合作
3,在平行ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90 ,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120 ,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数。
独立完成
4,如图,在正方形ABCD与等腰直角三角形BEF中,∠BEF=90 ,BE=EF,连接DF,点P是FD的中点,连接PE、PC.
(1)如图1,当点E在CB边上时,求证:CE = PE;
(2)如图2,当点E在CB的延长线上时,线段PC、CE有怎样的数量关系,写出你的猜想,并给与证明。
独立完成
独立完成
独立完成
独立完成
5.如图,在正方形ABCD中,点E,F分别为边BC,CD上的点,且AE⊥BF于点P,G为AD的中点,连接GP,过点P作PH⊥GP交AB于点H,连接GH.
(1)求证:BE=CF;
(2)若AB=6,BE= BC,求GH的长.
独立完成
独立完成
6.已知正方形ABCD内有一动点E,△CEF是以C为直角顶点的等腰直角三角形,连接EA、AF,M为AF中点,连接DM.
(1)如图(a),点E在正方形ABCD的对角线AC上,求证:EF∥AD;
(2)在(1)的条件下连接BE,如果BC=12,CE=4 ,求BE的长度;
(3)如图(b),求证:AE=2DM.
独立完成
例5:在矩形ABCD中,AE⊥BD于点E,点P是边AD上一点.
(1)若BP平分∠ABD,交AE于点G,PF⊥BD于点F,如图①,证明四边形AGFP是菱形;
(2)若PE⊥EC,如图②,求证:AE AB=DE AP;
(3)在(2)的条件下,若AB=1,BC=2,求AP的长.
模型一:角平分线上的点向两边作垂线
如图,P是∠MON平分线上一点,过点P作PA⊥OM于点A,PB⊥ON于点B,则PB=PA.
模型分析:
利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,为边相等、角相等,三角形全等创造更多的条件,进而可以快速找到解题的突破口。
角平分线模型
模型2 截取构造对称全等
如图,P是∠MON的平分线上一点,点A是射线OM上任意一点,在ON上截取OB=OA,连接PB,则△OPB≌△OPA.
模型分析:
利用角平分线图形的对称性,在角的两边构造对称全等三角形,可以得到对应边、对应角等.利用对称性把一些线段或角进行转移,这是经常使用的一种解题技巧.
模型三:角平分线+垂线构造等腰三角形
如图,P是∠MON的平分线上一点,AP⊥OP于P点,延长AP交ON于点B,则△AOB是等腰三角形.
模型分析:构造此模型可以利用等腰三角形的“三线合一,”也可以得到两个全等的直角三角形,进而得到对应边、对应角相等,这个模型巧妙地把角平分线和三线合一联系在一起.
四:角平分线+平行线
如图,P是∠MON的平分线上一点,过P点作PQ∥ON,交OM于点Q,则△POQ是等腰三角形.
模型分析:
有角平分线时,常过角平分线上一点作角的一边的平行线,构造等腰三角形,为证明结论提供更多的条件,体现了角平分线于等腰三角形之间的密切关系。
1.已知在矩形ABCD中,∠ADC的平分线DE与BC边交于点E,点P是线段DE上一定点(其中EP<PD),点F是CD延长线上一点,连接PF,过点P作PG⊥PF,交射线DA于点G.
(1)求证:PG=PF;(2)求证:DG=
DP+DF.
小组合作
2.如图,△ABC是直角三角形,且∠ABC=90°,四边形BCDE是平行四边形,E为AC的中点,BD平分∠ABC,点F在AB上,且BF = BC.
求证:
(1)DF = AE;
(2)DF⊥AC
小组合作
3.如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.
(1)求证:AC2=CD BC;
(2)过E作EG⊥AB,并延长EG至点K,使EK=EB.
①若点H是点D关于AC的对称点,点F为AC的中点,求证:FH⊥GH;
②若∠B=30°,求证:四边形AKEC是菱形.
独立完成
4.如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD.连接MF,NF.
(1)判断△BMN的形状,并证明你的结论;
(2)判断△MFN与△BDC之间的关系,并说明理由.
独立完成
例6:已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边长分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.
(1)如图①,当∠MAN点A旋转到BM=DN时,请你直接写出AH与AB的数量关系: ;
(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;
(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.
模型描述:
半角模型是指有公共顶点,锐角等于较大角的一半,且组成这个较大角的两边相等。通过翻折或旋转,将角的倍分关系转化为角的相等关系,并进一步构成全等或相似三角形,弱化条件,变更载体,而构建模型,可把握问题的本质。
模型图例:
半角模型
1.如图,在正方形ABCD中,BD为对角线,∠EAF=450, 其两边分别交BC、CD于E、F,交BD于H、G。
(1)求证:AD2=BG DH;
(2)求证:CE= DG;
(3)求证:EF= HG.
小组合作
2.在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN=45°.
如图1,当点M、N分别在线段BC、DC上时,写出线段BM、MN、DN之间的数量关系;并给予证明;
(2)如图2,当点M、N分别在CB、DC的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;
(3)如图3,当点M、N分别在CB、DC的延长线上时,若CN=CD=6,设BD与AM的延长线交于点P,交AN于Q,直接写出AQ、AP的长.
独立完成
例7:在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE感知如图①,过点A作AF⊥BE交BC于点F.求证△ABF≌△BCE.
探究如图②,取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(1)求证:BE=FG.
(2)连结CM,若CM=1,求FG的长.
应用如图③,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,求四边形GMCE的面积.
十字架模型
1:如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,
且AF⊥BE.
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.
小组合作
例8:如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系 ;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.
旋转模型
1.如图1,锐角△ABC中,分别以AB、AC为边向外作等边△ABE和等边△ACD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.
【深入探究】
(2)如图2,△ABC中,∠ABC=45°,AB=5cm,BC=3cm,分别以AB、AC为边向外作正方形ABNE和正方形ACMD,连接BD,求BD的长.
(3)如图3,在(2)的条件下,以AC为直角边在线段AC的左侧作等腰直角△ACD,求BD的长.
小组合作
2.如图, 在菱形ABCD中,∠ABC=600,点P是射线BD上一动点,以AP为边向右侧作等边△APE,点E的位置随着点P的位置变化而变化.
(1)如图1,当点E在菱形ABCD内部或边上时,连接CE,BP与CE的数量关系式______,CE与AD的位置关系是______;
(2)当点E在菱形ABCD外部时,(1)中的结论是否还成立,请予以证明;若不成立,请说明理由(选择图2、图3中的一种情况予以证明或说理);
(3)如图4,当点P在线段BD的延长线上时,连接BE,若AB=2,BE=2,求四边形ADPE的面积。
独立完成
例9:.已知,如图(1)在平行四边形ABCD中,点E,F分别在BC,CD上,且AE=AF,∠AEC=∠AFC.
(1)求证:四边形ABCD是菱形.
(2)如图(2),若AD=AF,延长AE,DC交于点G,求证:.
(3)在第(2)小题的条件下,连接BD,交AG于点H,若HE=4,EG=12,求AH的长.
相似及其他模型
1.如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)求证:EG2=2(1)AF.GF;
(3)若AG=6,EG=2,求BE的长。
小组合作
2.已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
(1)如图①,若四边形ABCD是矩形,且DE⊥CF,求证:CF:DE= CD:AD
(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,
使得CF:DE= CD:AD成立?并证明你的结论;
(3)如图③,若BA=BC=6,DA=DC=8,∠BAD=90°,DE⊥CF,求出CF:DE的值.
独立完成
圆
1.理解圆、弧、弦、圆心角、圆周角的概念,了解等圆、等弧的概念;探索并了解点与圆的位置关系。
2.探索并证明垂径定理:垂直于弦的直径平分弦以及弦所对的两条弧。
3.探索圆周角与圆心角及其所对弧的关系,了解并证明圆周角定理及其推论:圆周角的度数等于它所对弧上的圆心角度数的一半;直径所对的圆周角是直角;90°的圆周角所对的弦是直径;圆内接四边形的对角互补。
4.知道三角形的内心和外心。
5.了解直线和圆的位置关系,掌握切线的概念,探索切线与过切点的半径的关系,会用三角尺过圆上一点画圆的切线。
6.会计算圆的弧长、扇形的面积。
7.了解正多边形的概念及正多边形与圆的关系。
符合新课标的单元教学目标
圆专题
圆形
目标
1,掌握圆形相关基础知识(3课时)
2,学会把圆的问题转化成三角形和四边形(2课时)
模型
把圆的问题转化成三角形
把圆的问题转化成四边形
【考点总结】一、圆的有关概念及其对称性
1.圆的定义:
圆是平面内到定点的距离等于定长的所有点组成的图形.这个定点叫做圆心,定长叫做半径.
2.圆的对称性:
(1)圆的轴对称性:圆是轴对称图形,经过圆心的每一条直线都是它的对称轴;
(2)圆的中心对称性:圆是以圆心为对称中心的中心对称图形.
【考点总结】二、垂径定理
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
【考点总结】三、圆心角、弧、弦之间的关系
1.定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
2.推论:同圆或等圆中:
(1)两个圆心角相等;
(2)两条弧相等;
(3)两条弦相等.三项中有一项成立,则其余对应的两项也成立.
圆有关知识
【考点总结】四、圆心角与圆周角
1.定义:顶点在圆心上的角叫圆心角;顶点在圆上,角的两边和圆都相交的角叫圆周角.
2.性质:
(1)圆心角的度数等于它所对的弧的度数.
(2)一条弧所对的圆周角的度数等于它所对圆心角的度数的一半.
(3)同弧或等弧所对的圆周角相等,同圆或等圆中相等的圆周角所对的弧相等.
(4)半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
【考点总结】五、点与圆的位置关系
1.点和圆的位置关系:点在圆外,点在圆上,点在圆内.
2.过三点的圆
(1)经过三点的圆:
①经过在同一直线上的三点不能作圆;
②经过不在同一直线上的三点,有且只有一个圆.
(2)三角形的外心:经过三角形各顶点的圆叫做三角形的外接圆;外接圆的圆心叫做三角形的外心.
【考点总结】六、直线与圆的位置关系2-1-c-n-j-y
1.直线和圆的位置关系:相离、相切、相交.
2.概念:
(1)直线和圆有两个交点,这时我们就说这条直线和圆相交;
(2)直线和圆有唯一公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点;(3)直线和圆没有公共点,这时我们说这条直线和圆相离。
【考点总结】七、切线的判定和性质
1.切线的判定方法:
(1)经过半径的外端并且垂直于这条半径的直线是圆的切线;
(2)到圆心的距离等于半径的直线是圆的切线.
2.切线的性质:圆的切线垂直于经过切点的半径.
【考点总结】八、三角形(多边形)的内切圆
1.与三角形(多边形)内切圆有关的一些概念:
和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心.
2.三角形的内心的性质:
三角形的内心是三角形三条角平分线的交点,它到三边的距离相等,且在三角形内部.
【考点总结】九、弧长、扇形面积的计算
1.如果弧长为l,圆心角的度数为n°,圆的半径为r,那么弧长的计算公式为l=.
2.由组成圆心角的两条半径和圆心角所对弧围成的图形叫做扇形.若扇形的圆心角为n°,所在圆半径为r,弧长为l,面积为S为:
【考点总结】十、圆柱和圆锥
1.圆柱的侧面展开图是矩形,这个矩形的长等于圆柱的底面圆的周长,宽等于圆柱的高h.如果圆柱的底面半径是r,则S侧=2πrh,S全=2πr2+2πrh.
2.圆锥的轴截面与侧面展开图:轴截面为由母线、底面直径组成的等腰三角形.圆锥的侧面展开图是一个扇形,扇形的弧长等于圆锥的底面圆的周长,扇形的半径等于圆锥的母线长
因此圆锥的侧面积:S侧=l·2πr=πrl(l为母线长,r为底面圆半径);
圆锥的全面积:S全=S侧+S底=πrl+πr2.
例9:如图1,O为半圆的圆心,C、D为半圆上的两点,且 .连接AC并延长,与BD的延长线相交于点E.
(1)求证:CD=ED;
(2)AD与OC,BC分别交于点F,H.
①若CF=CH,如图2,求证:CF AF=FO AH;
②若圆的半径为2,BD=1,如图3,求AC的值.
=
1.如图,AB为⊙O直径,E为⊙O上一点,∠EAB的平分线AC交⊙O于点C,过C点作CD⊥AE的延长线于点D,直线CD与射线AB交于点P.
(1)判断直线DP与⊙O的位置关系,并说明理由;
(2)若DC=4,⊙O的半径为5,求PB的长.
小组合作
2如图①,四边形ABCD是正方形,点G是BC上的任意一点,BF⊥AG于点F,DE⊥AG于点E,探究BF,DE,EF之间的数量关系,并证明;
(2)如图③,四边形ABCD内接于⊙O,AB=AD,E,F是AC上的两点,且满足∠AED=∠BFA=∠BCD,试判断AC,DE,BF之间的数量关系,并说明理由.
独立完成
2.如图,四边形ABCD中,AB=AD=CD,以AB为直径⊙O的经过点C,连接AC、OD交于点E.
(1)证明:OD∥BC;
(2)若tan∠ABC=2,证明:DA与⊙O相切;
(3)在(2)条件下,连接BD交⊙O于点F,连接EF,若BC=1,求EF的长.
独立完成
1.(2019泰安14分)四边形ABCD是正方形,△EFC是等腰直角三角形,点E在AB上,且∠CEF=90°,FG⊥AD,垂足为点C.(1)试判断AG与FG是否相等?并给出证明;(2)若点H为CF的中点,GH与DH垂直吗?若垂直,给出证明;若不垂直,说明理由.
课后巩固联系
2021年东平一模考试23题
2021东平三模13分
在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.
(1)如图1,请直接写出线段OE与OF的数量关系和位置关系;
(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由;
尺规作图
例:如图,在四边形ABCD中,∠B=∠C=90°,AB>CD,AD=AB+CD.
(1)利用尺规作∠ADC的平分线DE,交BC于点E,连接AE(保留作图痕迹,不写作法);
(2)在(1)的条件下,
①证明:AE⊥DE;
②若CD=2,AB=4,点M,N分别是AE,AB上的动点,求BM+MN的最小值.
1.已知菱形的一个角与三角形的一个角重合,然后它的对角顶点在这个重合角的对边上,这个菱形称为这个三角形的亲密菱形,在△CFE中,CF=6,CE=12,∠FCE=45°,以点C为圆心,以任意长为半径作AD,再分别以点A和点D为圆心,大于 AD长为半径作弧,交EF于点B,AB∥CD.
(1)求证:四边形ACDB为△FEC的亲密菱形;
(2)求四边形ACDB的面积.
小组合作
2023年预测
当堂达标
课后习题
奇迹是会发生的,但你得为之拼命地努力.
——佚名
鲁教版中考数学复习
几何综合题
鲁教版五四制初中数学
几何综合题在中考中的地位:
对于中考数学,几何是永远绕不开的话题,往大方向说,谁吃透几何,谁就能占领中考的高分地,至少分数上肯定不会差。几何部分部分即是中考的重点,也是中考的难点,它包括全等、相似、计算以及添加辅助线等方方面面,是考题的重要组成部分,是考察综合能力的方式方法,正是由于这种综合性的特点,决定了相似三角形在中考中的重要地位。
整 体 结 构
几何综合题单元主要涉及到三角形,四边形和圆三大模块。1,三角形主要包括等腰三角形、等边三角形、直角三角形和一般三角形的全等和相似的证明。2,四边形主要包括平行四边形、菱形、矩形和正方形的判定和性质以及相关计算.3圆主要包括圆的有关概念和性质、圆的有关角和定理的应用和计算。
一:掌握相关图形的性质和判定定理
二:详细讲解几何相关例题
三:讲解与例题相关几何模型
四:小组合作解决问题
五:独立解决相关模型问题
主题问题单元设计
专题划分
三角形
课内8课时
课外3课时
四边形
课内12课时
课外4课时
圆
课内5课时
课外4课时
三角形
(1)理解三角形及其内角、外角、中线、高线、角平分线等概念,了解三角形的稳定性,探索并证明三角形的内角和定理.掌握它的推论。
(2)理解全等三角形的概念,能识别全等三角形中的对应边、对应角并能证明三角形全等。
(3)探索并证明角平分线的性质定理和线段垂直平分线的性质定理。
(4)了解等腰三角形和等边三角形的概念,探索并证明等腰三角形和等边三角形的性质定理和判定定理以及三线合一。
(5)了解直角三角形的概念探索并掌握直角三角形的性质定理和判定定理,直角三角形斜边上的中线等于斜边的一半,探索勾股定理及其逆定理,探索并掌握判定直角三角形全等的“斜边、直角边”定理。
符合新课标的单元教学目标
三角形专题
三角形
目标
1,掌握三角形相关基础知识(2课时)
2,掌握三角形有关模型的全等或相似证明(3课时)
3,完成三角形有关模型的全等或相似证明(3课时)
模型
手拉手模型
三垂直模型
相似模型
三角形有关的知识
【考点总结】一、三角形中的重要线段
1.三角形的高线:从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称高.
特性:三角形的三条高线相交于一点.
2.三角形的中线:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.特性:三角形的三条中线交于一点.
3.三角形的中位线:连接三角形两边中点的线段叫做三角形的中位线.
定理:三角形的中位线平行于第三边,且等于它的一半
4.三角形的角平分线:三角形一个角的平分线和这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.
特性:三角形的三条角平分线交于一点,这点叫做三角形的内心.
性质:角平分线上的点到角的两边的距离相等.
判定:角的内部到角的两边距离相等的点在角的平分线上,角的平分线可以看作是到角两边距离相等的点的集合.
5.线段垂直平分线:经过线段中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫中垂线.
性质:线段垂直平分线上的点到这条线段两个端点的距离相等.
判定:到一条线段的两个端点距离相等的点在线段的垂直平分线上,线段的垂直平分线可以看作是到线段两端点距离相等的点的集合.
【考点总结】二、等腰三角形及等边三角形的性质与判定
1.等腰三角形的有关概念及分类:有两边相等的三角形叫等腰三角形,三边相等的三角形叫做等边三角形,也叫正三角形;等腰三角形分为腰和底不相等的等
2.等腰三角形的性质:
(1)等腰三角形的两个底角相等(简称为“等边对等角”);
(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称为“三线合一”);
(3)等腰三角形是轴对称图形.
3.等腰三角形的判定:如果一个三角形有两个角相等,那么这两个角所对的边也相等.
4.等边三角形的性质:
(1)等边三角形的内角相等,且都等于60°;(2)等边三角形的三条边都相等.
5.等边三角形的判定:
(1)三条边相等的三角形是等边三角形;(2)三个角相等的三角形是等边三角形;
(3)有一个角为60°的等腰三角形是等边三角形.
【考点总结】三、直角三角形的有关性质和判定
1.直角三角形的有关性质
(1).直角三角形的两锐角互余.(2).直角三角形中,30°角所对的边等于斜边的一半.(3).直角三角形斜边上的中线等于斜边的一半.(4).勾股定理:直角三角形两直角边的平方和等于斜边的平方.
2.直角三角形的判定
(1).有一个角等于90°的三角形是直角三角形.(2).有两角互余的三角形是直角三角形.(3).如果三角形一边上的中线等于这边的一半,则该三角形是直角三角形.(4).勾股定理的逆定理:如果三角形一条边的平方等于另外两条边的平方和,那么这个三角形是直角三角形.
【考点总结】四、全等三角形的性质与判定
1.概念:能够完全重合的两个三角形叫做全等三角形.
2.性质:全等三角形的对应边、对应角分别相等.
3.判定:(1)有三边对应相等的两个三角形全等,简记为(SSS);
(2)有两边和它们的夹角对应相等的两个三角形全等,简记为(SAS);
(3)有两角和它们的夹边对应相等的两个三角形全等,简记为(ASA);
(4)有两角和其中一角的对边对应相等的两个三角形全等,简记为(AAS);
(5)有斜边和一条直角边对应相等的两个直角三角形全等,简记为(HL).
【考点总结】五、相似三角形
1.定义:
各角对应相等,各边对应成比例的两个三角形叫做相似三角形.
2.判定:
(1)平行于三角形一边的直线和其他两边(或两边延长线)相交,所构成的三角形与原三角形相似;
(2)两角对应相等,两三角形相似;
(3)两边对应成比例且夹角相等,两三角形相似;
(4)三边对应成比例,两三角形相似;
(5)斜边和一条直角边对应成比例,两直角三角形相似.
3.性质:
(1)相似三角形的对应角相等,对应边成比例;
(2)相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比;
(3)相似三角形周长的比等于相似比;
(4)相似三角形面积的比等于相似比的平方
例1.图1、图2中,点B为线段AE上一点,△ABC与△BED都是等边三角形。
(1)如图1,求证:AD=CE;
(2)如图2,设CE与AD交于点F,连接BF.
①求证:∠CFA=600;
②求证:CF+BF=AF.
典例讲解
在初中数学里,我们把两个有公共顶点且顶角相等的等腰三角形组成的图形叫手拉手模型。如下图①、图②、图③
手拉手模型
1.在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.
(1)如图1,点M,N分别在AD,AB上,且∠BMN=90°,当∠AMN=30°,AB=2时,求线段AM的长;
(2)如图2,点E,F分别在AB,AC上,且∠EDF=90°,求证:BE=AF;
(3)如图3,点M在AD的延长线上,点N在AC上,且∠BMN=90°,求证:AB+AN
AM.
小组合作
小组合作
2.如图,在等边三角形ABC中,点E是边AC上一定点,点D是直线BC上一动点,以DE为一边作等边三角形DEF,连接CF.
【问题解决】
如图1,若点D在边BC上,求证:CE+CF=CD;
【类比探究】
如图2,若点D在边BC的延长线上,请探究线段CE,CF与CD之间存在怎样的数量关系?并说明理由.
小组合作
3.【问题探究】
(1)如图1,△ABC和△DEC均为等腰直角三角形,∠ACB=∠DCE=90°,点B,D,E在同一直线上,连接AD,BD.点H.连接HF,AF,其中AF交EC于点M.
①请探究AD与BD之间的位置关系: ;
②若AC=BC=
,DC=CE=
,则线段AD的长为 ;
【拓展延伸】
(2)如图2,△ABC和△DEC均为直角三角形,∠ACB=∠DCE=90°,AC=
,BC=
,CD=
CE=1.将△DCE绕点C在平面内顺时针旋转,设旋转角∠BCD为α(0°≤α<360°),作直线BD,连接AD,当点B,D,E在同一直线上时,画出图形,并求线段AD的长.
手拉手模型分类
关于全等的手拉手模型有①②③④四类
①有公共顶点的等边三角形手拉手
②有公共顶点的等腰直角三角形手拉手
③共顶点且顶角相等的等腰三角形手拉手
④有公共顶点的正方形手拉手
关于相似的手拉手模型有⑤⑥两类
⑤有公共顶点的直角三角形手拉手
⑥有公共顶点的任意三角形手拉手
模型口诀:
等腰共顶手拉手,旋转全等马上有;
左手拉左手,右手拉右手,
两根拉线抖一抖,它们相等不用愁;
拉线夹角与顶角,相等互补答案有。
4.如图,△ABC中,∠BAC=90°,AB=AC,点D在直线BC上,△ADE是等腰直角三角形,∠DAE=90°,AD=AE,连接CE.
(1)当点D在线段BC上时,如图1,求证:DC+CE= AC;
(2)当点D在线段CB延长线上时,如图2,求证: AC=CD-CE
(3)当点D在线段BC延长线上时(如图3),探究线段DC、CE、AC之间的数量关系,并证明.
独立完成
5.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.
独立完成
6.已知△ABC 中,∠BAC=60°,以 AB 和 BC 为边向外作等边△ABD 和等边△BCE.
(1) 连接 AE、CD,如图 1,求证:AE=CD;
(2) 若 N 为 CD 中点,连接 AN,如图 2,求证:CE=2AN;
(3) 若 AB⊥BC,延长 AB 交 DE 于 M,DB=, 如图 3,则 BM= .(直接写出结果)
独立完成
典例讲解
例2如图,在Rt△ABC中,∠ABC=90°点D在BC的延长线上,且BD=AB.过点B作BE⊥AC,与BD的垂线DE交于点E.
(1)求证:△ABC≌△BDE;
(2)请找出线段AB、DE、CD之间的数量关系,并说明理由.
模型描述:
如图,已知△ABC是直角三角形,
∠BAC=90°,AC=BC,直线
l经过点C,分别从点B,A向直
线l作垂线,垂足分别为点D,E.
请证明:△ACD≌△CBE.
模型图例:
三垂直模型
1.在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.
(1)如图1,请直接写出线段OE与OF的数量关系和位置关系;
(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由;
(3)若|CF-AE|=2,EF=2,当△POF为等腰三角形时,请直接写出线段OP的长.
小组合作
例3在△ABC中,AD平分∠BAC交BC于点D,F为AD上一点,且BF=BD.BF的延长线交AC于点E.
(1)求证:AB AD=AF AC;
(2)若∠BAC=60°.AB=4,AC=6, 求DF的长;
典例讲解
相似模型
平行线型
斜交型
子母型
一线三等角型
小组合作
1.如图,△ABC中,∠ACB=90°,CB=CA,CE⊥AB于E,点F是CE上一点,连接AF并延长交BC于点D,CG⊥AD于点G,连接EG.
(1)求证:△DCG∽△DAC;
(2)如图1,若CF=2EF,求证:点D是BC中点;
(3)如图2,若GC=4,GE=4 ,求GD.
独立完成
2.已知:如图,在△ABC中,点D在边BC上,AE∥BC,BE与AD、AC分别相交于点F、G,
(1)求证:△CAD∽△CBG;
(2)连接DG,求证:
(3)若AB=AC=9,BC=6,点D是BC的中点,连接CE,求CE的长.
四边形
(1)了解多边形的定义,多边形的顶点、边、内角、外角、对角线等概念;探索并掌握多边形内角和与外角和公式.
(2)理解平行四边形、矩形、菱形、正方形的概念,以及它们之间的关系;了解四边形的不稳定性.
(3)探索并证明平行四边形的性质定理和判定定理
(4)了解两条平行线之间距离的意义,能度量两条平行线之间的距离.
(5)探索并证明矩形、菱形、正方形的性质定理和判定定理
符合新课标的单元教学目标
四边形专题
四边形
目标
1,掌握四边形相关基础知识(2课时)
2,掌握四边形有关模型的全等或相似证明(5课时)
3,完成四边形形有关模型的全等或相似证明(5课时)
模型
中 点 模 型
角平分线模型
半 角 模 型
旋 转 模 型
相似及其他模型
【考点总结】一、多边形的有关概念及性质
1.多边形的概念
定义:在平面内,由一些不在同一直线上的线段首尾顺次相接组成的图形叫做多边形.
对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
正多边形:各个角都相等,各条边都相等的多边形叫做正多边形.
2.性质:n边形的内角和为(n-2)·180°,外角和为360°.
【考点总结】二、平行四边形的定义和性质
1.定义:两组对边分别平行的四边形叫做平行四边形.
2.性质:
(1)平行四边形的对边相等且平行.
(2)平行四边形的对角相等.
(3)平行四边形的对角线互相平分.
(4)平行四边形是中心对称图形.
【考点总结】三、平行四边形的判定
1.两组对边分别相等的四边形是平行四边形.
2.两组对边分别平行的四边形是平行四边形.
3.一组对边平行且相等的四边形是平行四边形.
4.对角线相互平分的四边形是平行四边形.
5.两组对角分别相等的四边形是平行四边形.
四边形有关知识
【考点总结】四、矩形的性质与判定
1.定义:有一个角是直角的平行四边形是矩形.
2.性质:
(1)矩形的四个角都是直角.
(2)矩形的对角线相等.
(3)矩形既是轴对称图形,又是中心对称图形,它有两条对称轴;它的对称中心是对角线的交点.
3.判定:
(1)有三个角是直角的四边形是矩形.
(2)对角线相等的平行四边形是矩形.
(3)有一个角是直角的平行四边形是矩形.
【考点总结】五、菱形的性质与判定
1.定义:一组邻边相等的平行四边形叫做菱形.
2.性质:
(1)菱形的四条边都相等.
(2)菱形的对角线互相垂直且平分,并且每一条对角线平分一组对角.
3.判定:
(1)对角线互相垂直的平行四边形是菱形.
(2)四条边都相等的四边形是菱形.
(3)一组邻边相等的平行四边形叫做菱形.
【考点总结】六、正方形的性质与判定
1.定义:一组邻边相等的矩形叫做正方形.
2.性质:
(1)正方形的四条边都相等,四个角都是直角.
(2)正方形的对角线相等,且互相垂直平分;每条对角线平分一组对角.
(3)正方形是轴对称图形,两条对角线所在直线,以及过每一组对边中点的直线都是它的对称轴;正方形是中心对称图形,对角线的交点是它的对称中心.21世纪教育网版权所有
3.判定:
(1)一组邻边相等并且有一个角是直角的平行四边形是正方形.
(2)一组邻边相等的矩形是正方形.
(3)对角线互相垂直的矩形是正方形.
(4)有一个角是直角的菱形是正方形.
例4如图,△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点, FG⊥BC于点G,与DE交于点H,若FG=AF, AG平分∠BAC,连接GE, ;GD.
(1)求证:△ECG≌△GHD
(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论.
(3)若∠B=300,判定四边形AEGF是否为菱形,并说明理由.
1、倍长中线:遇到线段的中点问题,常借助倍长中线的方法还原中心对称图形,利用“8”字形全等将题中条件集中,达到解题的目的,这种方法是最常用的也是最重要的方法, 在△ABC中,M为BC边的中点:
(1)如图1,连结AM并延长至点F,使得ME=AM,连结CE.则△ABM≌△ECM;
(2)如图2,点D在AB边上,连结DM并延长至点E,使得ME=DM,连结CE,则△BDM≌△CEM。
中点模型
2、构造中位线:三角形的中位线从位置关系和数量关系两方面将将图形中分散的线段关系集中起来,通常需要再找一个中点来构造中位线,或者倍长某线段构造中位线,在△ABC中,D为AB边的中点,则:
(1)如图1,取AC边的中点E,连结DE,则DE//BC,且DF=0.5BC.
(2)如图2,延长BC至点F,使得CF=BC,连结CD,AF,则DC//AF,且DC=0.5AE。
3、等腰三角形“三线合一”。如图,在△ABC中,若AB=AC;通常取底边BC的中点D,则AD⊥BC,且AD平分∠BAC。事实上,在△ABC中:①AB=AC;②AD平分∠BAC;③BD=CD,④AD⊥BC;对于以上四条语句,任意选择两个作为条件,就可以推出另两条结论,即“知二得二”。
4、直角三角形斜边中线。如图,在△ABC看,∠ABC=900,取AC的中点D,连结BD,则有BD=AD=CD=AC;反过来,在△ABC中,点D在AC边上,若BD=AD=CD=0.5AC,则有∠ABC=90°。
1.已知两个等腰Rt△ABC,Rt△CEF有公共顶点C,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;
(2)如图2,当∠BCE=45°时,求证:BM=ME.
小组合作
小组合作
2.如图,四边形ABCD是平行四边形,AD=AC,AD⊥AC,E是AB的中点,F是AC延长线上一点.
(1)若ED⊥EF,求证:ED=EF;
(2)在(1)的条件下,若DC的延长线与FB交于点P,试判定四边形ACPE是否为平行四边形 并证明你的结论(请先补全图形,再解答);
(3)若ED=EF,ED与EF垂直吗 若垂直给出证明.
小组合作
3,在平行ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明CE=CF;
(2)若∠ABC=90 ,G是EF的中点(如图2),直接写出∠BDG的度数;
(3)若∠ABC=120 ,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数。
独立完成
4,如图,在正方形ABCD与等腰直角三角形BEF中,∠BEF=90 ,BE=EF,连接DF,点P是FD的中点,连接PE、PC.
(1)如图1,当点E在CB边上时,求证:CE = PE;
(2)如图2,当点E在CB的延长线上时,线段PC、CE有怎样的数量关系,写出你的猜想,并给与证明。
独立完成
独立完成
独立完成
独立完成
5.如图,在正方形ABCD中,点E,F分别为边BC,CD上的点,且AE⊥BF于点P,G为AD的中点,连接GP,过点P作PH⊥GP交AB于点H,连接GH.
(1)求证:BE=CF;
(2)若AB=6,BE= BC,求GH的长.
独立完成
独立完成
6.已知正方形ABCD内有一动点E,△CEF是以C为直角顶点的等腰直角三角形,连接EA、AF,M为AF中点,连接DM.
(1)如图(a),点E在正方形ABCD的对角线AC上,求证:EF∥AD;
(2)在(1)的条件下连接BE,如果BC=12,CE=4 ,求BE的长度;
(3)如图(b),求证:AE=2DM.
独立完成
例5:在矩形ABCD中,AE⊥BD于点E,点P是边AD上一点.
(1)若BP平分∠ABD,交AE于点G,PF⊥BD于点F,如图①,证明四边形AGFP是菱形;
(2)若PE⊥EC,如图②,求证:AE AB=DE AP;
(3)在(2)的条件下,若AB=1,BC=2,求AP的长.
模型一:角平分线上的点向两边作垂线
如图,P是∠MON平分线上一点,过点P作PA⊥OM于点A,PB⊥ON于点B,则PB=PA.
模型分析:
利用角平分线的性质:角平分线上的点到角两边的距离相等,构造模型,为边相等、角相等,三角形全等创造更多的条件,进而可以快速找到解题的突破口。
角平分线模型
模型2 截取构造对称全等
如图,P是∠MON的平分线上一点,点A是射线OM上任意一点,在ON上截取OB=OA,连接PB,则△OPB≌△OPA.
模型分析:
利用角平分线图形的对称性,在角的两边构造对称全等三角形,可以得到对应边、对应角等.利用对称性把一些线段或角进行转移,这是经常使用的一种解题技巧.
模型三:角平分线+垂线构造等腰三角形
如图,P是∠MON的平分线上一点,AP⊥OP于P点,延长AP交ON于点B,则△AOB是等腰三角形.
模型分析:构造此模型可以利用等腰三角形的“三线合一,”也可以得到两个全等的直角三角形,进而得到对应边、对应角相等,这个模型巧妙地把角平分线和三线合一联系在一起.
四:角平分线+平行线
如图,P是∠MON的平分线上一点,过P点作PQ∥ON,交OM于点Q,则△POQ是等腰三角形.
模型分析:
有角平分线时,常过角平分线上一点作角的一边的平行线,构造等腰三角形,为证明结论提供更多的条件,体现了角平分线于等腰三角形之间的密切关系。
1.已知在矩形ABCD中,∠ADC的平分线DE与BC边交于点E,点P是线段DE上一定点(其中EP<PD),点F是CD延长线上一点,连接PF,过点P作PG⊥PF,交射线DA于点G.
(1)求证:PG=PF;(2)求证:DG=
DP+DF.
小组合作
2.如图,△ABC是直角三角形,且∠ABC=90°,四边形BCDE是平行四边形,E为AC的中点,BD平分∠ABC,点F在AB上,且BF = BC.
求证:
(1)DF = AE;
(2)DF⊥AC
小组合作
3.如图,在四边形ABCD中,AC平分∠BCD,AC⊥AB,E是BC的中点,AD⊥AE.
(1)求证:AC2=CD BC;
(2)过E作EG⊥AB,并延长EG至点K,使EK=EB.
①若点H是点D关于AC的对称点,点F为AC的中点,求证:FH⊥GH;
②若∠B=30°,求证:四边形AKEC是菱形.
独立完成
4.如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD.连接MF,NF.
(1)判断△BMN的形状,并证明你的结论;
(2)判断△MFN与△BDC之间的关系,并说明理由.
独立完成
例6:已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边长分别交CB、DC(或它们的延长线)于点M、N,AH⊥MN于点H.
(1)如图①,当∠MAN点A旋转到BM=DN时,请你直接写出AH与AB的数量关系: ;
(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;
(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,NH=3,求AH的长.
模型描述:
半角模型是指有公共顶点,锐角等于较大角的一半,且组成这个较大角的两边相等。通过翻折或旋转,将角的倍分关系转化为角的相等关系,并进一步构成全等或相似三角形,弱化条件,变更载体,而构建模型,可把握问题的本质。
模型图例:
半角模型
1.如图,在正方形ABCD中,BD为对角线,∠EAF=450, 其两边分别交BC、CD于E、F,交BD于H、G。
(1)求证:AD2=BG DH;
(2)求证:CE= DG;
(3)求证:EF= HG.
小组合作
2.在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN=45°.
如图1,当点M、N分别在线段BC、DC上时,写出线段BM、MN、DN之间的数量关系;并给予证明;
(2)如图2,当点M、N分别在CB、DC的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;
(3)如图3,当点M、N分别在CB、DC的延长线上时,若CN=CD=6,设BD与AM的延长线交于点P,交AN于Q,直接写出AQ、AP的长.
独立完成
例7:在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE感知如图①,过点A作AF⊥BE交BC于点F.求证△ABF≌△BCE.
探究如图②,取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(1)求证:BE=FG.
(2)连结CM,若CM=1,求FG的长.
应用如图③,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,求四边形GMCE的面积.
十字架模型
1:如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,
且AF⊥BE.
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.
小组合作
例8:如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系 ;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.
旋转模型
1.如图1,锐角△ABC中,分别以AB、AC为边向外作等边△ABE和等边△ACD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.
【深入探究】
(2)如图2,△ABC中,∠ABC=45°,AB=5cm,BC=3cm,分别以AB、AC为边向外作正方形ABNE和正方形ACMD,连接BD,求BD的长.
(3)如图3,在(2)的条件下,以AC为直角边在线段AC的左侧作等腰直角△ACD,求BD的长.
小组合作
2.如图, 在菱形ABCD中,∠ABC=600,点P是射线BD上一动点,以AP为边向右侧作等边△APE,点E的位置随着点P的位置变化而变化.
(1)如图1,当点E在菱形ABCD内部或边上时,连接CE,BP与CE的数量关系式______,CE与AD的位置关系是______;
(2)当点E在菱形ABCD外部时,(1)中的结论是否还成立,请予以证明;若不成立,请说明理由(选择图2、图3中的一种情况予以证明或说理);
(3)如图4,当点P在线段BD的延长线上时,连接BE,若AB=2,BE=2,求四边形ADPE的面积。
独立完成
例9:.已知,如图(1)在平行四边形ABCD中,点E,F分别在BC,CD上,且AE=AF,∠AEC=∠AFC.
(1)求证:四边形ABCD是菱形.
(2)如图(2),若AD=AF,延长AE,DC交于点G,求证:.
(3)在第(2)小题的条件下,连接BD,交AG于点H,若HE=4,EG=12,求AH的长.
相似及其他模型
1.如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)求证:EG2=2(1)AF.GF;
(3)若AG=6,EG=2,求BE的长。
小组合作
2.已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
(1)如图①,若四边形ABCD是矩形,且DE⊥CF,求证:CF:DE= CD:AD
(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,
使得CF:DE= CD:AD成立?并证明你的结论;
(3)如图③,若BA=BC=6,DA=DC=8,∠BAD=90°,DE⊥CF,求出CF:DE的值.
独立完成
圆
1.理解圆、弧、弦、圆心角、圆周角的概念,了解等圆、等弧的概念;探索并了解点与圆的位置关系。
2.探索并证明垂径定理:垂直于弦的直径平分弦以及弦所对的两条弧。
3.探索圆周角与圆心角及其所对弧的关系,了解并证明圆周角定理及其推论:圆周角的度数等于它所对弧上的圆心角度数的一半;直径所对的圆周角是直角;90°的圆周角所对的弦是直径;圆内接四边形的对角互补。
4.知道三角形的内心和外心。
5.了解直线和圆的位置关系,掌握切线的概念,探索切线与过切点的半径的关系,会用三角尺过圆上一点画圆的切线。
6.会计算圆的弧长、扇形的面积。
7.了解正多边形的概念及正多边形与圆的关系。
符合新课标的单元教学目标
圆专题
圆形
目标
1,掌握圆形相关基础知识(3课时)
2,学会把圆的问题转化成三角形和四边形(2课时)
模型
把圆的问题转化成三角形
把圆的问题转化成四边形
【考点总结】一、圆的有关概念及其对称性
1.圆的定义:
圆是平面内到定点的距离等于定长的所有点组成的图形.这个定点叫做圆心,定长叫做半径.
2.圆的对称性:
(1)圆的轴对称性:圆是轴对称图形,经过圆心的每一条直线都是它的对称轴;
(2)圆的中心对称性:圆是以圆心为对称中心的中心对称图形.
【考点总结】二、垂径定理
垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
【考点总结】三、圆心角、弧、弦之间的关系
1.定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
2.推论:同圆或等圆中:
(1)两个圆心角相等;
(2)两条弧相等;
(3)两条弦相等.三项中有一项成立,则其余对应的两项也成立.
圆有关知识
【考点总结】四、圆心角与圆周角
1.定义:顶点在圆心上的角叫圆心角;顶点在圆上,角的两边和圆都相交的角叫圆周角.
2.性质:
(1)圆心角的度数等于它所对的弧的度数.
(2)一条弧所对的圆周角的度数等于它所对圆心角的度数的一半.
(3)同弧或等弧所对的圆周角相等,同圆或等圆中相等的圆周角所对的弧相等.
(4)半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
【考点总结】五、点与圆的位置关系
1.点和圆的位置关系:点在圆外,点在圆上,点在圆内.
2.过三点的圆
(1)经过三点的圆:
①经过在同一直线上的三点不能作圆;
②经过不在同一直线上的三点,有且只有一个圆.
(2)三角形的外心:经过三角形各顶点的圆叫做三角形的外接圆;外接圆的圆心叫做三角形的外心.
【考点总结】六、直线与圆的位置关系2-1-c-n-j-y
1.直线和圆的位置关系:相离、相切、相交.
2.概念:
(1)直线和圆有两个交点,这时我们就说这条直线和圆相交;
(2)直线和圆有唯一公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点;(3)直线和圆没有公共点,这时我们说这条直线和圆相离。
【考点总结】七、切线的判定和性质
1.切线的判定方法:
(1)经过半径的外端并且垂直于这条半径的直线是圆的切线;
(2)到圆心的距离等于半径的直线是圆的切线.
2.切线的性质:圆的切线垂直于经过切点的半径.
【考点总结】八、三角形(多边形)的内切圆
1.与三角形(多边形)内切圆有关的一些概念:
和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心.
2.三角形的内心的性质:
三角形的内心是三角形三条角平分线的交点,它到三边的距离相等,且在三角形内部.
【考点总结】九、弧长、扇形面积的计算
1.如果弧长为l,圆心角的度数为n°,圆的半径为r,那么弧长的计算公式为l=.
2.由组成圆心角的两条半径和圆心角所对弧围成的图形叫做扇形.若扇形的圆心角为n°,所在圆半径为r,弧长为l,面积为S为:
【考点总结】十、圆柱和圆锥
1.圆柱的侧面展开图是矩形,这个矩形的长等于圆柱的底面圆的周长,宽等于圆柱的高h.如果圆柱的底面半径是r,则S侧=2πrh,S全=2πr2+2πrh.
2.圆锥的轴截面与侧面展开图:轴截面为由母线、底面直径组成的等腰三角形.圆锥的侧面展开图是一个扇形,扇形的弧长等于圆锥的底面圆的周长,扇形的半径等于圆锥的母线长
因此圆锥的侧面积:S侧=l·2πr=πrl(l为母线长,r为底面圆半径);
圆锥的全面积:S全=S侧+S底=πrl+πr2.
例9:如图1,O为半圆的圆心,C、D为半圆上的两点,且 .连接AC并延长,与BD的延长线相交于点E.
(1)求证:CD=ED;
(2)AD与OC,BC分别交于点F,H.
①若CF=CH,如图2,求证:CF AF=FO AH;
②若圆的半径为2,BD=1,如图3,求AC的值.
=
1.如图,AB为⊙O直径,E为⊙O上一点,∠EAB的平分线AC交⊙O于点C,过C点作CD⊥AE的延长线于点D,直线CD与射线AB交于点P.
(1)判断直线DP与⊙O的位置关系,并说明理由;
(2)若DC=4,⊙O的半径为5,求PB的长.
小组合作
2如图①,四边形ABCD是正方形,点G是BC上的任意一点,BF⊥AG于点F,DE⊥AG于点E,探究BF,DE,EF之间的数量关系,并证明;
(2)如图③,四边形ABCD内接于⊙O,AB=AD,E,F是AC上的两点,且满足∠AED=∠BFA=∠BCD,试判断AC,DE,BF之间的数量关系,并说明理由.
独立完成
2.如图,四边形ABCD中,AB=AD=CD,以AB为直径⊙O的经过点C,连接AC、OD交于点E.
(1)证明:OD∥BC;
(2)若tan∠ABC=2,证明:DA与⊙O相切;
(3)在(2)条件下,连接BD交⊙O于点F,连接EF,若BC=1,求EF的长.
独立完成
1.(2019泰安14分)四边形ABCD是正方形,△EFC是等腰直角三角形,点E在AB上,且∠CEF=90°,FG⊥AD,垂足为点C.(1)试判断AG与FG是否相等?并给出证明;(2)若点H为CF的中点,GH与DH垂直吗?若垂直,给出证明;若不垂直,说明理由.
课后巩固联系
2021年东平一模考试23题
2021东平三模13分
在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.
(1)如图1,请直接写出线段OE与OF的数量关系和位置关系;
(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由;
尺规作图
例:如图,在四边形ABCD中,∠B=∠C=90°,AB>CD,AD=AB+CD.
(1)利用尺规作∠ADC的平分线DE,交BC于点E,连接AE(保留作图痕迹,不写作法);
(2)在(1)的条件下,
①证明:AE⊥DE;
②若CD=2,AB=4,点M,N分别是AE,AB上的动点,求BM+MN的最小值.
1.已知菱形的一个角与三角形的一个角重合,然后它的对角顶点在这个重合角的对边上,这个菱形称为这个三角形的亲密菱形,在△CFE中,CF=6,CE=12,∠FCE=45°,以点C为圆心,以任意长为半径作AD,再分别以点A和点D为圆心,大于 AD长为半径作弧,交EF于点B,AB∥CD.
(1)求证:四边形ACDB为△FEC的亲密菱形;
(2)求四边形ACDB的面积.
小组合作
2023年预测
当堂达标
课后习题
奇迹是会发生的,但你得为之拼命地努力.
——佚名
