【大单元教学】鲁教版2023年八年级大单元 第八章 一元二次方程 课件(21张PPT)
文档属性
| 名称 | 【大单元教学】鲁教版2023年八年级大单元 第八章 一元二次方程 课件(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 253.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
一元二次方程
课标要求:
1、理解配方法,能用配方法、公式法、因式分解法解数字系数的一元二次方程。
2、会用一元二次方程根的判别式判别方程是否有实根及两个实根是否相等。
3、了解一元二次方程的根与系数的关系(例 67)。
4、能根据具体问题的实际意义,检验方程解的合理性。
单元内容:
1、理解配方法,能用配方法、公式法、因式分解法解数字系数的一元二次方程。
2、会用一元二次方程根的判别式判别方程是否有实根及两个实根是否相等。
3、了解一元二次方程的根与系数的关系。
4、能根据具体问题的实际意义,检验方程解的合理性。
5、能列一元二次方程解应用题。
单元目标:
1、理解配方法,能用配方法、公式法、因式分解法解数字系数的一元二次方程。
2、会用一元二次方程根的判别式判别方程是否有实根及两个实根是否相等。
3、了解一元二次方程的根与系数的关系。
4、能根据具体问题的实际意义,检验方程解的合理性。
5、能列一元二次方程解应用题。
单元学情:
对学生已知内容的掌握程度可通过检测反馈进行了解,对学生的学习方法、学习习惯、兴趣等的了解要在平时的学习中进行充分的观察了解。对新知内容如何设计尝试自学,对未知内容一遇到学习障碍如何能突破,同时在学习中本单元有何特点、习惯怎样、兴趣如何要及时提前做好充分的了解。
作业设计:
本单元作业尽可能做到面向全体学生,进行分层分类设计,做到单元教学设计整体评价和单元课程资源合理利用。
课时设计:
第8章一元二次方程
(共17课时) 8.1一元二次方程 2课时
8.2用配方法解一元二次方程 3课时
8.3用公式法解一元二次方程 3课时
8.4用因式分解法解一元二次方程 1课时
8.5*一元二次方程的根与系数的关系(※) 1课时
8.6一元二次方程的应用 4课时
回顾与总结 3课时
一元二次方程的概念及解法
1.一元二次方程的概念:只含有①一个未知数,且未知数的最高次数是②2的整式方程,叫做一元二次方程.它的一般形式是③ax2+bx+c=0(a≠0).
【注意】 对于方程ax2+bx+c=0,只有当④a≠0时才是一元二次方程.如果说ax2+bx+c=0是一元二次方程,那么必然隐含着⑤a≠0.
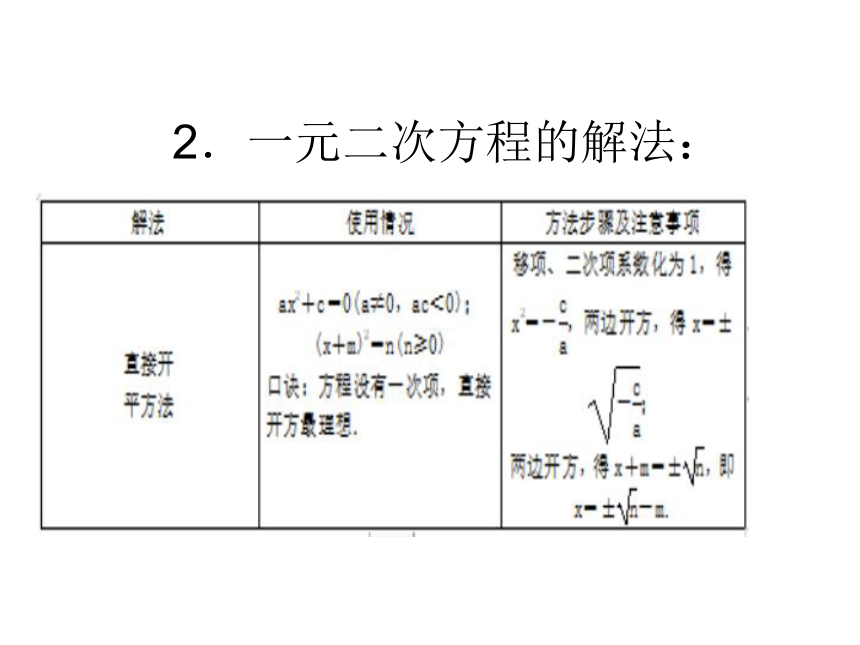
2.一元二次方程的解法:
一元二次方程根的判别式
1.根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根的情况可由⑧b2-4ac来判定,我们将⑨b2-4ac称为根的判别式.
2.判别式与根的关系:
(1)b2-4ac>0 方程有两个⑩不相等的实数根;
(2)b2-4ac=0 方程有两个 相等的实数根;
(3)b2-4ac<0 方程 没有实数根.
3.关于x的一元二次方程(k-1)x2+4x+1=0.
(1)若有两个相等的实数根,则k的值是5;
(2)若有两个不相等的实数根,则k的取值范围是k<5且k≠1;
(3)若没有实数根,则k的取值范围是k>5;
(4)若有实数根,则k的取值范围是k≤5且k≠1.
【变式提问】 若关于x的方程(k-1)x2+4x+1=0有实数根,则k的取值范围是k≤5.
【易错提示】 在使用根的判别式解决问题时,如果二次项系数中含有字母,那么要加上二次项系数不为0这个限制条件.
一元二次方程根与系数的关系
当b2-4ac≥0时,一元二次方程ax2+bx+c=0有两个实数根x1,x2,则有:x1+x2= -,x1x2= .
一元二次方程的解与系数a,b,c的关系
(1)当c=0时,方程ax2+bx+c=0(a≠0)必有一解为x=0;
(2)当a+b+c=0时,方程ax2+bx+c=0(a≠0)必有一解为x=1;
(3)当a-b+c=0时,方程ax2+bx+c=0(a≠0)必有一解为x=-1.
一元二次方程的应用
常见类型及其关系式
1.增长率问题:
设基础量是a,每次增长的百分率为x,则第一次增长后为 a(1+x);第二次增长后为 a(1+x)2.若增长两次后的量为b,则有 a(1+x)2=b.
如图1,设空白部分的宽为x,则S阴影= (a-2x)(b-2x);
如图2、图3、图4,设阴影道路的宽为x,则S空白= (a-x)(b-x);
如图5,长为a,宽为b的矩形ABCD的四个角都剪去一个边长为x的正方形后做成一个无盖的盒子,则该盒子的底面积S= (a-2x)(b-2x);
5.(1)某药品经过两次降价,每瓶零售价由100元降为81元.已知两次降价的百分率都为x,那么x满足的方程是100(1-x)2=81;
(2)某机械厂七月份生产零件100万个,九月份生产零件196万个,设该厂八、九月份平均每月的增长率为x,则x满足的方程是100(1+x)2=196.
6.如图,在长60 m、宽40 m的矩形花园中,欲修宽度相等的观赏路(如阴影部分所示),要使观赏路面积占总面积的,则路宽x(m)应满足的方程是(40-2x)(60-3x)=(1-)×60×40.
7.春节期间x个老同学聚会.
(1)若每两个人都握一次手,所有人共握手28次,则所列方程为x(x-1)=28;
(2)若每人给其他成员赠送一张贺卡,所有人共送贺卡56张,则所列方程为x(x-1)=56.
8.新世纪百货大楼“宝乐”牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”儿童节,商场决定采取适当的降价措施.经调查,如果每件童装降价2元,那么平均每天就可多售出4件.要想平均每天销售这种童装盈利1 200元,则每件童装应降价多少元?设每件童装应降价x元,可列方程为(40-x)(20+×4)=1200.
基础小练:
一元二次方程根的判别式及根与系数的关系
(2020·随州)已知关于x的一元二次方程x2+(2m+1)x+m-2=0.
(1)求证:无论m取何值,此方程总有两个不相等的实数根.
(2)若方程有两个实数根x1,x2,且x1+x2+3x1x2=1,求m的值.
【思路点拨】 (1)根据根的判别式得出Δ=(2m+1)2-4×1×(m-2)=4m2+9>0,据此可得答案;(2)根据根与系数的关系得出x1+x2=-(2m+1),x1x2=m-2,代入x1+x2+3x1x2=1得出关于m的方程,解之可得答案.
【自主解答】 解:(1)证明:∵Δ=(2m+1)2-4×1×(m-2)
=4m2+4m+1-4m+8=4m2+9>0,
∴无论m取何值,此方程总有两个不相等的实数根.
(2)由根与系数的关系,得x1+x2=-(2m+1),x1x2=m-2.
由x1+x2+3x1x2=1,得-(2m+1)+3(m-2)=1.
解得m=8.
重点练习
一元二次方程根的判别式及根与系数的关系
(2020·随州)已知关于x的一元二次方程x2+(2m+1)x+m-2=0.
(1)求证:无论m取何值,此方程总有两个不相等的实数根.
(2)若方程有两个实数根x1,x2,且x1+x2+3x1x2=1,求m的值.
【思路点拨】 (1)根据根的判别式得出Δ=(2m+1)2-4×1×(m-2)=4m2+9>0,据此可得答案;(2)根据根与系数的关系得出x1+x2=-(2m+1),x1x2=m-2,代入x1+x2+3x1x2=1得出关于m的方程,解之可得答案.
【自主解答】 解:(1)证明:∵Δ=(2m+1)2-4×1×(m-2)
=4m2+4m+1-4m+8
=4m2+9>0,
∴无论m取何值,此方程总有两个不相等的实数根.
(2)由根与系数的关系,得x1+x2=-(2m+1),x1x2=m-2.
由x1+x2+3x1x2=1,得-(2m+1)+3(m-2)=1.
解得m=8.
一元二次方程
课标要求:
1、理解配方法,能用配方法、公式法、因式分解法解数字系数的一元二次方程。
2、会用一元二次方程根的判别式判别方程是否有实根及两个实根是否相等。
3、了解一元二次方程的根与系数的关系(例 67)。
4、能根据具体问题的实际意义,检验方程解的合理性。
单元内容:
1、理解配方法,能用配方法、公式法、因式分解法解数字系数的一元二次方程。
2、会用一元二次方程根的判别式判别方程是否有实根及两个实根是否相等。
3、了解一元二次方程的根与系数的关系。
4、能根据具体问题的实际意义,检验方程解的合理性。
5、能列一元二次方程解应用题。
单元目标:
1、理解配方法,能用配方法、公式法、因式分解法解数字系数的一元二次方程。
2、会用一元二次方程根的判别式判别方程是否有实根及两个实根是否相等。
3、了解一元二次方程的根与系数的关系。
4、能根据具体问题的实际意义,检验方程解的合理性。
5、能列一元二次方程解应用题。
单元学情:
对学生已知内容的掌握程度可通过检测反馈进行了解,对学生的学习方法、学习习惯、兴趣等的了解要在平时的学习中进行充分的观察了解。对新知内容如何设计尝试自学,对未知内容一遇到学习障碍如何能突破,同时在学习中本单元有何特点、习惯怎样、兴趣如何要及时提前做好充分的了解。
作业设计:
本单元作业尽可能做到面向全体学生,进行分层分类设计,做到单元教学设计整体评价和单元课程资源合理利用。
课时设计:
第8章一元二次方程
(共17课时) 8.1一元二次方程 2课时
8.2用配方法解一元二次方程 3课时
8.3用公式法解一元二次方程 3课时
8.4用因式分解法解一元二次方程 1课时
8.5*一元二次方程的根与系数的关系(※) 1课时
8.6一元二次方程的应用 4课时
回顾与总结 3课时
一元二次方程的概念及解法
1.一元二次方程的概念:只含有①一个未知数,且未知数的最高次数是②2的整式方程,叫做一元二次方程.它的一般形式是③ax2+bx+c=0(a≠0).
【注意】 对于方程ax2+bx+c=0,只有当④a≠0时才是一元二次方程.如果说ax2+bx+c=0是一元二次方程,那么必然隐含着⑤a≠0.
2.一元二次方程的解法:
一元二次方程根的判别式
1.根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根的情况可由⑧b2-4ac来判定,我们将⑨b2-4ac称为根的判别式.
2.判别式与根的关系:
(1)b2-4ac>0 方程有两个⑩不相等的实数根;
(2)b2-4ac=0 方程有两个 相等的实数根;
(3)b2-4ac<0 方程 没有实数根.
3.关于x的一元二次方程(k-1)x2+4x+1=0.
(1)若有两个相等的实数根,则k的值是5;
(2)若有两个不相等的实数根,则k的取值范围是k<5且k≠1;
(3)若没有实数根,则k的取值范围是k>5;
(4)若有实数根,则k的取值范围是k≤5且k≠1.
【变式提问】 若关于x的方程(k-1)x2+4x+1=0有实数根,则k的取值范围是k≤5.
【易错提示】 在使用根的判别式解决问题时,如果二次项系数中含有字母,那么要加上二次项系数不为0这个限制条件.
一元二次方程根与系数的关系
当b2-4ac≥0时,一元二次方程ax2+bx+c=0有两个实数根x1,x2,则有:x1+x2= -,x1x2= .
一元二次方程的解与系数a,b,c的关系
(1)当c=0时,方程ax2+bx+c=0(a≠0)必有一解为x=0;
(2)当a+b+c=0时,方程ax2+bx+c=0(a≠0)必有一解为x=1;
(3)当a-b+c=0时,方程ax2+bx+c=0(a≠0)必有一解为x=-1.
一元二次方程的应用
常见类型及其关系式
1.增长率问题:
设基础量是a,每次增长的百分率为x,则第一次增长后为 a(1+x);第二次增长后为 a(1+x)2.若增长两次后的量为b,则有 a(1+x)2=b.
如图1,设空白部分的宽为x,则S阴影= (a-2x)(b-2x);
如图2、图3、图4,设阴影道路的宽为x,则S空白= (a-x)(b-x);
如图5,长为a,宽为b的矩形ABCD的四个角都剪去一个边长为x的正方形后做成一个无盖的盒子,则该盒子的底面积S= (a-2x)(b-2x);
5.(1)某药品经过两次降价,每瓶零售价由100元降为81元.已知两次降价的百分率都为x,那么x满足的方程是100(1-x)2=81;
(2)某机械厂七月份生产零件100万个,九月份生产零件196万个,设该厂八、九月份平均每月的增长率为x,则x满足的方程是100(1+x)2=196.
6.如图,在长60 m、宽40 m的矩形花园中,欲修宽度相等的观赏路(如阴影部分所示),要使观赏路面积占总面积的,则路宽x(m)应满足的方程是(40-2x)(60-3x)=(1-)×60×40.
7.春节期间x个老同学聚会.
(1)若每两个人都握一次手,所有人共握手28次,则所列方程为x(x-1)=28;
(2)若每人给其他成员赠送一张贺卡,所有人共送贺卡56张,则所列方程为x(x-1)=56.
8.新世纪百货大楼“宝乐”牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”儿童节,商场决定采取适当的降价措施.经调查,如果每件童装降价2元,那么平均每天就可多售出4件.要想平均每天销售这种童装盈利1 200元,则每件童装应降价多少元?设每件童装应降价x元,可列方程为(40-x)(20+×4)=1200.
基础小练:
一元二次方程根的判别式及根与系数的关系
(2020·随州)已知关于x的一元二次方程x2+(2m+1)x+m-2=0.
(1)求证:无论m取何值,此方程总有两个不相等的实数根.
(2)若方程有两个实数根x1,x2,且x1+x2+3x1x2=1,求m的值.
【思路点拨】 (1)根据根的判别式得出Δ=(2m+1)2-4×1×(m-2)=4m2+9>0,据此可得答案;(2)根据根与系数的关系得出x1+x2=-(2m+1),x1x2=m-2,代入x1+x2+3x1x2=1得出关于m的方程,解之可得答案.
【自主解答】 解:(1)证明:∵Δ=(2m+1)2-4×1×(m-2)
=4m2+4m+1-4m+8=4m2+9>0,
∴无论m取何值,此方程总有两个不相等的实数根.
(2)由根与系数的关系,得x1+x2=-(2m+1),x1x2=m-2.
由x1+x2+3x1x2=1,得-(2m+1)+3(m-2)=1.
解得m=8.
重点练习
一元二次方程根的判别式及根与系数的关系
(2020·随州)已知关于x的一元二次方程x2+(2m+1)x+m-2=0.
(1)求证:无论m取何值,此方程总有两个不相等的实数根.
(2)若方程有两个实数根x1,x2,且x1+x2+3x1x2=1,求m的值.
【思路点拨】 (1)根据根的判别式得出Δ=(2m+1)2-4×1×(m-2)=4m2+9>0,据此可得答案;(2)根据根与系数的关系得出x1+x2=-(2m+1),x1x2=m-2,代入x1+x2+3x1x2=1得出关于m的方程,解之可得答案.
【自主解答】 解:(1)证明:∵Δ=(2m+1)2-4×1×(m-2)
=4m2+4m+1-4m+8
=4m2+9>0,
∴无论m取何值,此方程总有两个不相等的实数根.
(2)由根与系数的关系,得x1+x2=-(2m+1),x1x2=m-2.
由x1+x2+3x1x2=1,得-(2m+1)+3(m-2)=1.
解得m=8.
