【大单元教学】鲁教版2023年八年级大单元 第九章 图形的相似 课件(48张PPT)
文档属性
| 名称 | 【大单元教学】鲁教版2023年八年级大单元 第九章 图形的相似 课件(48张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1023.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 00:00:00 | ||
图片预览










文档简介
(共48张PPT)
第9章 图形的相似
1
对接课标 单元架构
2
知识梳理 整合提升
3
典题自测 迎战中考
目
录
对接课标 单元架构
1
图形的相似
1.比例线段:比例线段的意义,比例性质及平行线分线段成比例。
2.相似三角形:判定,性质(中位线,重心及性质)
3.相似多边形:判定和性质
4.位似多边形: 概念,性质和作法
5.图形变换和坐标: 平移,对称和位似
①了解比例的基本性质、线段的比、成比例的线段。
②通过具体实例认识图形的相似。了解相似多边形和相似比。
③掌握基本事实:两条直线被一组平行线所截,所得的对应线段 成比例。
④了解相似三角形的判定定理:两角分别相等的两个三角形相 似;两边成比例且夹角相等的两个三角形相似;三边成比例的两个三 角形相似。了解相似三角形判定定理的证明。
⑤了解相似三角形的性质定理 :相似三角形对应线段的比等于 相似比;面积比等于相似比的平方。
⑥了解图形的位似,知道利用位似可以将一个图形放大或缩小。
⑦会利用图形的相似解决一些简单的实际问题。
新课标教学目标
2
知识梳理 整合提升
一、成比例线段
对于四条线段a、b、c、d,如果其中两条线段的长度的比等于另外两条线段的比, 如 (或a∶b=c∶d),那么,这四条线段叫做成比例线段,简称比例线段.此时也称这四条线段成比例.
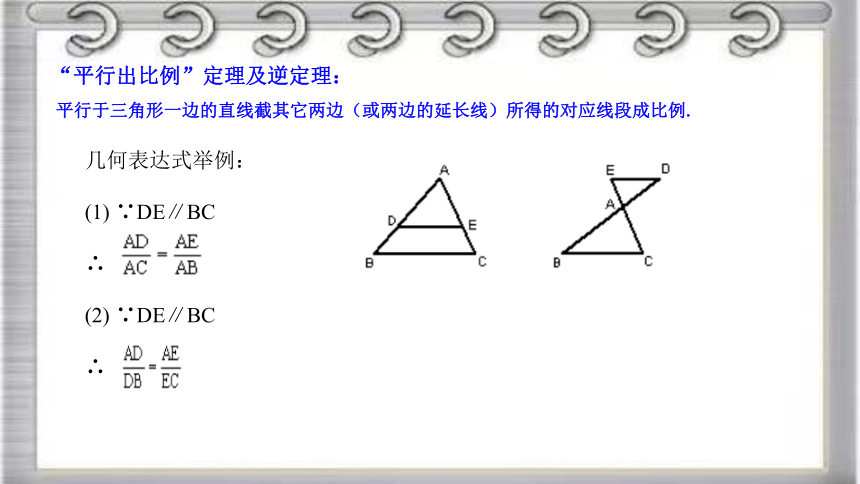
“平行出比例”定理及逆定理:
平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例.
几何表达式举例:
(1) ∵DE∥BC
∴
(2) ∵DE∥BC
∴
比例的性质
①基本性质:
②合比性质:
③等比性质:
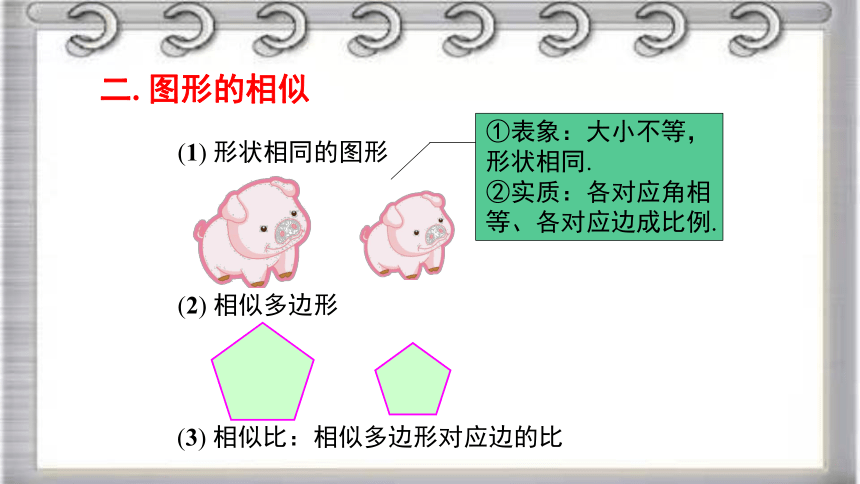
(1) 形状相同的图形
(2) 相似多边形
(3) 相似比:相似多边形对应边的比
二. 图形的相似
①表象:大小不等,形状相同.
②实质:各对应角相等、各对应边成比例.
1.各角对应相等,各边对应成比例的两个多边形叫相似多边形。
2.三个角对应相等,三条边对应成比例的两个三角形叫相似三角形.两个相似三角形用“∽”表示,读做“相似于”。
3.相似三角形对应边的比,叫做相似比
相似图形
如△A1B1C1与△ABC相似,
注意:对应顶点写在对应位置上
记作“△A1B1C1∽△ABC”
相似比=对应边的比值=
方法2: 平行于三角形一边的直线与其他两边(或延 长线)相交,所构成的三角形与原三角形相似;
方法5: 三边对应成比例的,两三角形相似.
三、相似三角形的判定方法
方法4: 两边对应成比例且夹角相等,两三角形相似.
方法1:通过定义(不常用)
方法3: 两对应角相等的,两三角形相似.
相似三角形的基本图形
相似三角形的基本图形
1.定理:“平行”出相似
平行于三角形一边的直线截其它两边(或其他两边的延长线),所构成的三角形与原三角形相似.
几何表达式举例:
∵DE∥BC
∴ΔADE∽ΔABC
2.定理:“AA”出相似
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
几何表达式举例:
∵∠A=∠A
又∵∠AED=∠ACB
∴ΔADE∽ΔABC
3.定理:“SAS”出相似
如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.
几何表达式举例:
∵
又∵∠A=∠A
∴ΔADE∽ΔABC
4.定理:“SSS”出相似
如果两个三角形的三边对应成比例,那么这两个三角形相似.
∽
∵
∴
A
B
C
对应角相等、对应边成比例
对应高、中线、角平分线的比等于相似比
周长比等于相似比
面积比等于相似比的平方
四. 相似三角形的性质
1. 如图,已知:△ABC中,DE∥BC,AD=3,DB=6,AE=2,求AC的长.
解:∵DE∥BC,
∴△ADE∽△ABC.
∴
又∵AD=3,DB=6,AE=2,
∴
解得EC=4.
∴AC=AE+EC=6.
2:如图,D、E分别是△ABC的边AC、AB上的点.AE=1.5,AC=2,BC=3,且 ,求DE的长。
A
E
D
C
B
试说明∠BAD=∠CAE.
A
D
C
E
B
3.
测高
(不能直接使用皮尺或刻度尺量的)
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决.
五. 相似三角形的应用
1.如图,身高为1.6m的某同学想测量一棵大树的高度,她沿树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树高为( )
A、4.8m B、6.4m
C、8m D、10m
D
A
C
B
E
解:依题意知:EC⊥AB,于点C,DB⊥AB于点B,
∴CE∥DB
∴△ACE∽△ABD
∴AC:AB=CE:BD
∵AC=0.8m,BC=3.2m
∴AB=AC+CB=4m CE=1.6m
∴0.8:4=1.6:BD
解得:BD=8(m)
∴树高BD为8m。
六、图形的位似
如果两个图形不仅是相似图形,而且是每组对应点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形.
★这个点叫做位似中心.
★这两个相似图形的相似比又称为位似比.
★位似图形上任意一对对应点到位似中心的距离之比等于位似比.
位似多边形的性质
(1)位似多边形是相似多边形,
(2)各对应点所在的直线交于位似中心
(3)位似多边形上任意一对对应点到位似中心的距离之比等于相似比.
(4)位似多边形中的对应线段平行(或在一条直线上).
2.如图,△ABC和△DEF是以点O为位似中心的位似图形,OA:AD=2:3,
△ABC的周长为8,则△DEF的周长为为 .
3.如图,△ABC与△DEF位似,点O为位似中心,已知OA:OD=2:5,
则△ABC与△DEF的面积比为 .
3
典题自测 迎战期末
1.如果 ,那么 =___;如果ad=bc(a、b、c、d都不为0),那么 .
2. 三角形一边的直线和其他两边(或两边的延长线)相交所构成的三角形与原三角形相似.
3.相似三角形对应角 ,对应边 .
4. 的两个三角形相似.
5.相似三角形面积的比等于相似比的 ;周长的比等于 ;对应高、对应中线、对应角平分线的比等于 .
ad
bc
平行于
相等
成比例
两角分别相等;两边成比例且夹角相等;三边成比例
平方
相似比
相似比
6. 如图,在 □ABCD 中,点 E 在边 BC 上,BE : EC =1 : 2,连接 AE 交 BD 于点 F,则 △BFE 的面积与 △DFA 的面积之比为 .
7.如图,已知∠ACD=∠B,BD=5,AD=4,求AC的长.
8.如图,等边三角形△ACB的边长为3,点P为BC上的一点,点D为AC上的一点,
连接AP、PD,∠APD=60°.
(1)求证:△ABP∽△PCD;
(2)若PC=2,求CD的长.
9.如图,在边长为4的正方形ABCD中,P是BC上的点,且BP=3PC,
Q是CD的中点,求证:△ADQ∽△QCP.
10.如图,△ABC与△ADE中,∠ACB=∠AED=90°,连接BD、CE,
∠EAC=∠DAB.
(1)求证:△ABC∽△ADE;
(2)求证:△BAD∽△CAE.
11.如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A出发,以1cm/s的速度
沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点
同时停止运动.设点P、Q运动时间为t(s).当△PBQ与△ABC相似时,t的值是多少?
12.如图,矩形ABCD中,E为DC上一点,把△ADE沿AE翻折,点D恰好落在
BC边上的点F处.
(1)求证:△ABF∽△FCE;
(2)若AB=2 ,AD=4,求DE的长.
13.如图,Rt△ABC中,∠ACB=90°,AC=BC,P为△ABC内部一点,且
∠APB=∠BPC=135°.
求证:(1)△PAB∽△PBC; (2)PC= PA.
14.如图,在等边△ABC中,点D是AB边上的一个动点(不与点A,B重合),
以CD为边作等边△EDC,AC与DE交于点F,连接AE.
(1)求证:△ADF∽△BCD;
(2)若AB:BD=3:1,且AB=12,求△ADF的面积.
15.如图,∠ABD=∠BCD=90°,DB平分∠ADC,过点B作BM∥CD交AD于M.
连接CM交DB于N.
(1)求证:BD2=AD CD;
(2)若CD=6,AD=8,求MN的长.
16.如图,在等腰△ABC中,AB=AC,BD为AC上的高,BE⊥AB交AC延长线于E.
(1)求证:AC2=AD AE;
(2)点F为BC中点,延长AF交BE于G,求证:△BCD∽△AGB.
(3)在(2)的条件下,若CD=2,BD=6,求AB的长.
17.如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达点E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高是1.5米,那么路灯A的高度AB是( )
A.4.5米 B.6米
C.7.2米 D.8米
谢谢欣赏
第9章 图形的相似
1
对接课标 单元架构
2
知识梳理 整合提升
3
典题自测 迎战中考
目
录
对接课标 单元架构
1
图形的相似
1.比例线段:比例线段的意义,比例性质及平行线分线段成比例。
2.相似三角形:判定,性质(中位线,重心及性质)
3.相似多边形:判定和性质
4.位似多边形: 概念,性质和作法
5.图形变换和坐标: 平移,对称和位似
①了解比例的基本性质、线段的比、成比例的线段。
②通过具体实例认识图形的相似。了解相似多边形和相似比。
③掌握基本事实:两条直线被一组平行线所截,所得的对应线段 成比例。
④了解相似三角形的判定定理:两角分别相等的两个三角形相 似;两边成比例且夹角相等的两个三角形相似;三边成比例的两个三 角形相似。了解相似三角形判定定理的证明。
⑤了解相似三角形的性质定理 :相似三角形对应线段的比等于 相似比;面积比等于相似比的平方。
⑥了解图形的位似,知道利用位似可以将一个图形放大或缩小。
⑦会利用图形的相似解决一些简单的实际问题。
新课标教学目标
2
知识梳理 整合提升
一、成比例线段
对于四条线段a、b、c、d,如果其中两条线段的长度的比等于另外两条线段的比, 如 (或a∶b=c∶d),那么,这四条线段叫做成比例线段,简称比例线段.此时也称这四条线段成比例.
“平行出比例”定理及逆定理:
平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例.
几何表达式举例:
(1) ∵DE∥BC
∴
(2) ∵DE∥BC
∴
比例的性质
①基本性质:
②合比性质:
③等比性质:
(1) 形状相同的图形
(2) 相似多边形
(3) 相似比:相似多边形对应边的比
二. 图形的相似
①表象:大小不等,形状相同.
②实质:各对应角相等、各对应边成比例.
1.各角对应相等,各边对应成比例的两个多边形叫相似多边形。
2.三个角对应相等,三条边对应成比例的两个三角形叫相似三角形.两个相似三角形用“∽”表示,读做“相似于”。
3.相似三角形对应边的比,叫做相似比
相似图形
如△A1B1C1与△ABC相似,
注意:对应顶点写在对应位置上
记作“△A1B1C1∽△ABC”
相似比=对应边的比值=
方法2: 平行于三角形一边的直线与其他两边(或延 长线)相交,所构成的三角形与原三角形相似;
方法5: 三边对应成比例的,两三角形相似.
三、相似三角形的判定方法
方法4: 两边对应成比例且夹角相等,两三角形相似.
方法1:通过定义(不常用)
方法3: 两对应角相等的,两三角形相似.
相似三角形的基本图形
相似三角形的基本图形
1.定理:“平行”出相似
平行于三角形一边的直线截其它两边(或其他两边的延长线),所构成的三角形与原三角形相似.
几何表达式举例:
∵DE∥BC
∴ΔADE∽ΔABC
2.定理:“AA”出相似
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
几何表达式举例:
∵∠A=∠A
又∵∠AED=∠ACB
∴ΔADE∽ΔABC
3.定理:“SAS”出相似
如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.
几何表达式举例:
∵
又∵∠A=∠A
∴ΔADE∽ΔABC
4.定理:“SSS”出相似
如果两个三角形的三边对应成比例,那么这两个三角形相似.
∽
∵
∴
A
B
C
对应角相等、对应边成比例
对应高、中线、角平分线的比等于相似比
周长比等于相似比
面积比等于相似比的平方
四. 相似三角形的性质
1. 如图,已知:△ABC中,DE∥BC,AD=3,DB=6,AE=2,求AC的长.
解:∵DE∥BC,
∴△ADE∽△ABC.
∴
又∵AD=3,DB=6,AE=2,
∴
解得EC=4.
∴AC=AE+EC=6.
2:如图,D、E分别是△ABC的边AC、AB上的点.AE=1.5,AC=2,BC=3,且 ,求DE的长。
A
E
D
C
B
试说明∠BAD=∠CAE.
A
D
C
E
B
3.
测高
(不能直接使用皮尺或刻度尺量的)
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决.
五. 相似三角形的应用
1.如图,身高为1.6m的某同学想测量一棵大树的高度,她沿树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树高为( )
A、4.8m B、6.4m
C、8m D、10m
D
A
C
B
E
解:依题意知:EC⊥AB,于点C,DB⊥AB于点B,
∴CE∥DB
∴△ACE∽△ABD
∴AC:AB=CE:BD
∵AC=0.8m,BC=3.2m
∴AB=AC+CB=4m CE=1.6m
∴0.8:4=1.6:BD
解得:BD=8(m)
∴树高BD为8m。
六、图形的位似
如果两个图形不仅是相似图形,而且是每组对应点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形.
★这个点叫做位似中心.
★这两个相似图形的相似比又称为位似比.
★位似图形上任意一对对应点到位似中心的距离之比等于位似比.
位似多边形的性质
(1)位似多边形是相似多边形,
(2)各对应点所在的直线交于位似中心
(3)位似多边形上任意一对对应点到位似中心的距离之比等于相似比.
(4)位似多边形中的对应线段平行(或在一条直线上).
2.如图,△ABC和△DEF是以点O为位似中心的位似图形,OA:AD=2:3,
△ABC的周长为8,则△DEF的周长为为 .
3.如图,△ABC与△DEF位似,点O为位似中心,已知OA:OD=2:5,
则△ABC与△DEF的面积比为 .
3
典题自测 迎战期末
1.如果 ,那么 =___;如果ad=bc(a、b、c、d都不为0),那么 .
2. 三角形一边的直线和其他两边(或两边的延长线)相交所构成的三角形与原三角形相似.
3.相似三角形对应角 ,对应边 .
4. 的两个三角形相似.
5.相似三角形面积的比等于相似比的 ;周长的比等于 ;对应高、对应中线、对应角平分线的比等于 .
ad
bc
平行于
相等
成比例
两角分别相等;两边成比例且夹角相等;三边成比例
平方
相似比
相似比
6. 如图,在 □ABCD 中,点 E 在边 BC 上,BE : EC =1 : 2,连接 AE 交 BD 于点 F,则 △BFE 的面积与 △DFA 的面积之比为 .
7.如图,已知∠ACD=∠B,BD=5,AD=4,求AC的长.
8.如图,等边三角形△ACB的边长为3,点P为BC上的一点,点D为AC上的一点,
连接AP、PD,∠APD=60°.
(1)求证:△ABP∽△PCD;
(2)若PC=2,求CD的长.
9.如图,在边长为4的正方形ABCD中,P是BC上的点,且BP=3PC,
Q是CD的中点,求证:△ADQ∽△QCP.
10.如图,△ABC与△ADE中,∠ACB=∠AED=90°,连接BD、CE,
∠EAC=∠DAB.
(1)求证:△ABC∽△ADE;
(2)求证:△BAD∽△CAE.
11.如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A出发,以1cm/s的速度
沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动.当点Q到达点C时,P、Q两点
同时停止运动.设点P、Q运动时间为t(s).当△PBQ与△ABC相似时,t的值是多少?
12.如图,矩形ABCD中,E为DC上一点,把△ADE沿AE翻折,点D恰好落在
BC边上的点F处.
(1)求证:△ABF∽△FCE;
(2)若AB=2 ,AD=4,求DE的长.
13.如图,Rt△ABC中,∠ACB=90°,AC=BC,P为△ABC内部一点,且
∠APB=∠BPC=135°.
求证:(1)△PAB∽△PBC; (2)PC= PA.
14.如图,在等边△ABC中,点D是AB边上的一个动点(不与点A,B重合),
以CD为边作等边△EDC,AC与DE交于点F,连接AE.
(1)求证:△ADF∽△BCD;
(2)若AB:BD=3:1,且AB=12,求△ADF的面积.
15.如图,∠ABD=∠BCD=90°,DB平分∠ADC,过点B作BM∥CD交AD于M.
连接CM交DB于N.
(1)求证:BD2=AD CD;
(2)若CD=6,AD=8,求MN的长.
16.如图,在等腰△ABC中,AB=AC,BD为AC上的高,BE⊥AB交AC延长线于E.
(1)求证:AC2=AD AE;
(2)点F为BC中点,延长AF交BE于G,求证:△BCD∽△AGB.
(3)在(2)的条件下,若CD=2,BD=6,求AB的长.
17.如图,小明晚上由路灯A下的点B处走到点C处时,测得自身影子CD的长为1米,他继续往前走3米到达点E处(即CE=3米),测得自己影子EF的长为2米,已知小明的身高是1.5米,那么路灯A的高度AB是( )
A.4.5米 B.6米
C.7.2米 D.8米
谢谢欣赏
