【大单元教学】鲁教版2023年八年级大单元 第九章图形的相似 课件(51张PPT)
文档属性
| 名称 | 【大单元教学】鲁教版2023年八年级大单元 第九章图形的相似 课件(51张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 22.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 11:21:46 | ||
图片预览







文档简介
(共51张PPT)
1.重点
2.考点
3.命题点
1.了解比例的基本性质、线段的比、成比例的线段;通过建筑、艺术上的实例了解黄金分割.
2.掌握基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
3.了解相似三角形的性质定理和判定定理.
4.通过具体实例认识图形的相似,了解相似多边形和相似比.
5.会利用图形的相似解决一些简单的实际问题.
6.了解相似三角形判定定理的证明.
图形的相似
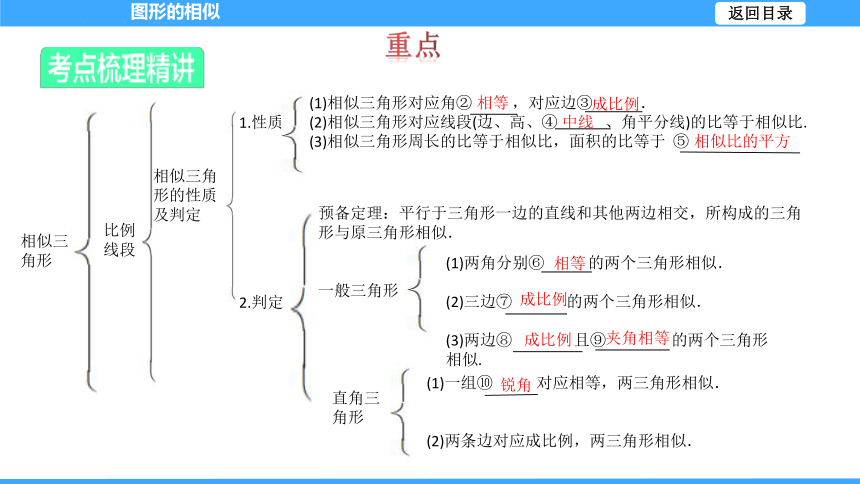
重点
相似三角形
比例线段
比例性质
平行线分线段成比例
第五讲 相似三角形
交叉相乘积相等:
①
=
(abcd≠0)
(1)基本事实:两条直线被一组平行线所截,所,得的线段成比例.如图1,图2,当l1∥l2∥,l3时,
(2)推论:平行于三角形一边的直线截其他两边(或两边的延长,线),所得的线段成比例.如图3,当DE∥BC时,有=
ad=bc
重点
图形的相似
相似三角形
比例线段
相似三角形的性质及判定
第五讲 相似三角形
1.性质
2.判定
(1)相似三角形对应角② ,对应边③ .
(2)相似三角形对应线段(边、高、④ 、角平分线)的比等于相似比.
(3)相似三角形周长的比等于相似比,面积的比等于 ⑤
预备定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
一般三角形
(1)两角分别⑥ 的两个三角形相似.
(2)三边⑦ 的两个三角形相似.
(3)两边⑧ 且⑨ 的两个三角形相似.
直角三角形
(1)一组⑩ 对应相等,两三角形相似.
(2)两条边对应成比例,两三角形相似.
相等
成比例
中线
相似比的平方
相等
成比例
成比例
夹角相等
锐角
重点
图形的相似
发
相似三角形
相似多边形的性质及判定
第五讲 相似三角形
1.性质
2.判定
(1)对应角相等,对应边 .
(2)对应边的比、周长的比都等于 ,面积的比等于 .
(1)对应角相等,对应边成比例的多边形是相似多边形.
(2)所有对应边成比例,那么这两个多边形是相似多边形.
相似三角形的实际运用
1.步骤
2.常考类型
(1)将实际问题转化为相似三角形问题.
(2)找出一对相似三角形.
(3)根据相似三角形的性质,表示出相应的量,并求解.
(1)利用光的反射定律求物体的高度.
(2)利用影子计算建筑物的高度(同一时刻,物高与影长成正比例,有:=.
(3)构造相似三角形计算不能直接测量的物体的高度(宽度).
成比例
相似比
相似比的平方
重点
图形的相似
相似三角形
图形的位似
第五讲 相似三角形
定义 :如果两个图形不仅是相似图形,而且每组对应点所在直线都经过同一点,那么这两个图,形叫做位似图形,这个点叫做位似中心
2.性质
3.位似变换与坐标的关系:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标等于k 或
(1)位似图形上的任意一对对应点到位似中心的距离之比等于 ,面积比等,于相似比的平方.
(2)位似图形对应点的连线或延长线相交于同一点.
(3)位似图形对应边 且成比例.
(4)位似图形对应角 .
相似比
平行(或共线)
相等
-k
重点
图形的相似
第五讲 相似三角形
一、相似三角形的判定
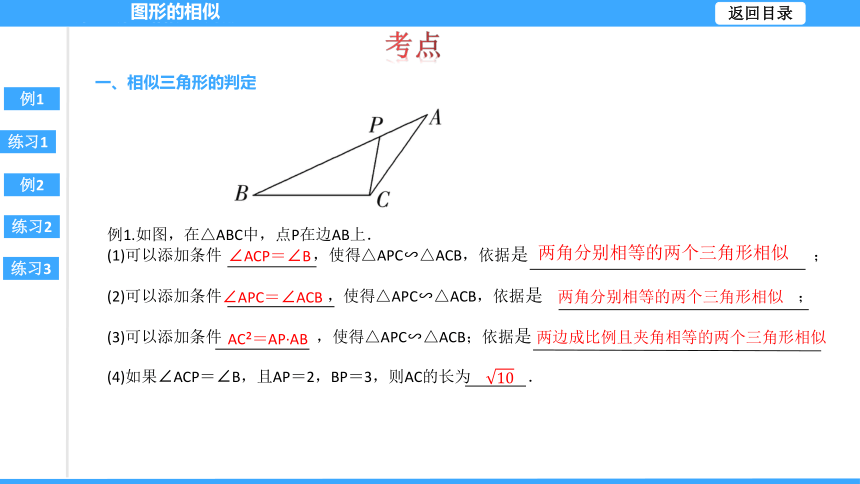
例1.如图,在△ABC中,点P在边AB上.
(1)可以添加条件 ,使得△APC∽△ACB,依据是 ;
(2)可以添加条件 ,使得△APC∽△ACB,依据是 ;
(3)可以添加条件 ,使得△APC∽△ACB;依据是
(4)如果∠ACP=∠B,且AP=2,BP=3,则AC的长为.
∠ACP=∠B
两角分别相等的两个三角形相似
∠APC=∠ACB
两角分别相等的两个三角形相似
AC =AP·AB
两边成比例且夹角相等的两个三角形相似
考点
图形的相似
第五讲 相似三角形
练习1.如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.图中相似三角形有
解析:∵∠BAD=∠CAE,∠BAD+∠DAC=∠CAE+∠DAC,即∠BAC=∠DAE.
又∵∠ABC=∠ADE,
∴△ABC∽△ADE.∵△ABC∽△ADE,
∴=
又∵∠BAD=∠CAE,
∴△ABD∽△ACE.
△ABC∽△ADE,△ABD∽△ACE.
考点
图形的相似
第五讲 相似三角形
二、相似三角形的判定和性质
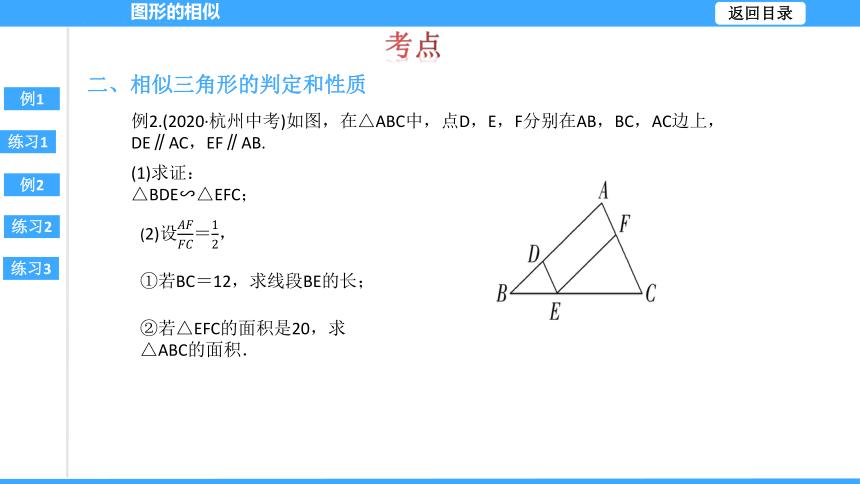
例2.(2020·杭州中考)如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC;
(2)设=,
①若BC=12,求线段BE的长;
②若△EFC的面积是20,求△ABC的面积.
考点
图形的相似
第五讲 相似三角形
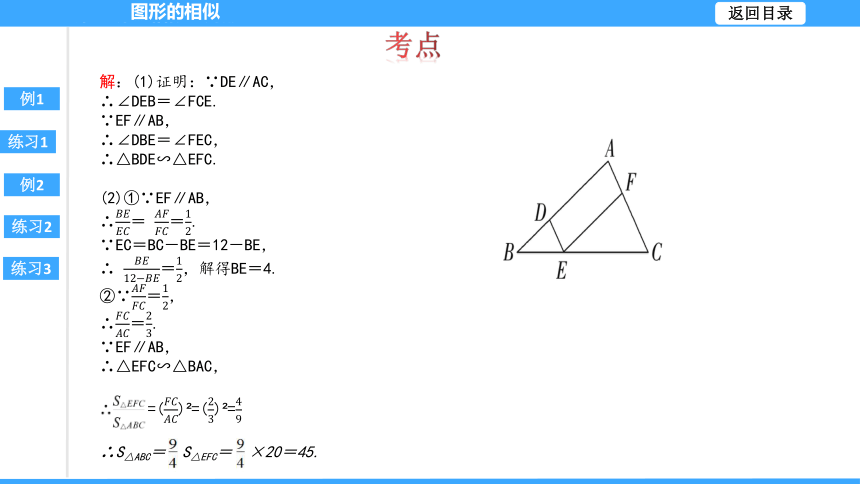
解:(1)证明:∵DE∥AC,
∴∠DEB=∠FCE.
∵EF∥AB,
∴∠DBE=∠FEC,
∴△BDE∽△EFC.
(2)①∵EF∥AB,
∴= =.
∵EC=BC-BE=12-BE,
∴ =,解得BE=4.
②∵=,
∴=.
∵EF∥AB,
∴△EFC∽△BAC,
=() =() =
∴S△ABC= S△EFC= ×20=45.
考点
图形的相似
第五讲 相似三角形
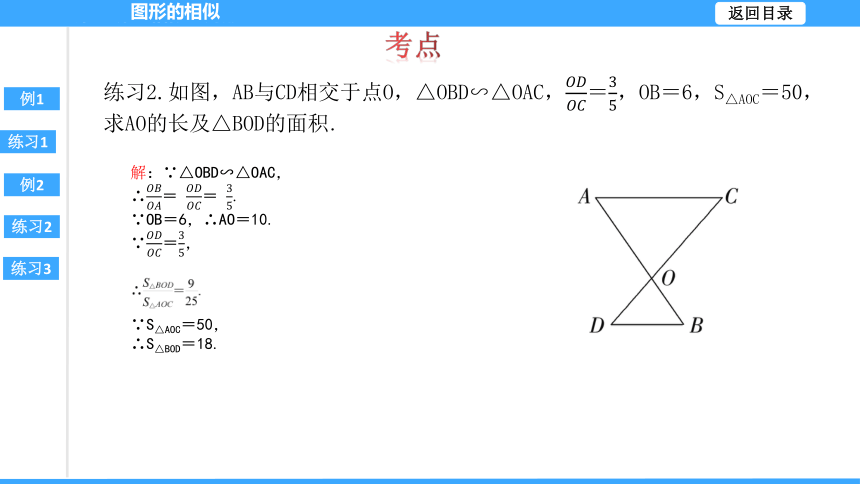
练习2.如图,AB与CD相交于点O,△OBD∽△OAC,=,OB=6,S△AOC=50,求AO的长及△BOD的面积.
解:∵△OBD∽△OAC,∴= = .
∵OB=6,∴AO=10.
∵=,
∵S△AOC=50,
∴S△BOD=18.
考点
图形的相似
第五讲 相似三角形
练习3.如图,在△ABC中,BC=120,高AD=60,正方形EFGH一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,求AN的长.
解:设正方形EFGH的边长EF=EH=x.
∵四边形EFGH是正方形,
∴∠HEF=∠EHG=90°,EF∥BC,
∴△AEF∽△ABC.
∵AD是△ABC的高,
∴∠HDN=90°,
∴四边形EHDN是矩形,
∴DN=EH=x.
∵△AEF∽△ABC,
∴=.
∵BC=120,AD=60,
∴AN=60-x,
∴ =,解得x=40,
∴AN=60-x=60-40=20.
考点
图形的相似
第五讲 相似三角形
命题点 成比例的线段
1.如果=,那么的值是( )
A.3 B.-3 C. D.-
解析:∵ = ,∴ b=2a ∴原式= =
B
命题点
图形的相似
第五讲 相似三角形
解析:设 == =k,则x=2k,y=3k,z=4k,
∴=== .
2.(2021·大庆中考)已知,则=___.
命题点
图形的相似
2
第五讲 相似三角形
命题点 平行线分线段成比例
C
3.(2021·淄博中考)如图,AB,CD相交于点E,且AC∥EF∥DB,点C,F,B在同一条直线上.已知AC=p,EF=r,DB=q,则p,q,r之间满足的数量关系式是( )
命题点
图形的相似
第五讲 相似三角形
4.★如图,在△ABC中,点D在BC边上,连接AD,点E在AC边上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是( )
A.= B.=
C.= D.=
解析:∵EF∥BC,
∴= .
∵EG∥AB,
∴ =
C
命题点
图形的相似
3
第五讲 相似三角形
命题点 相似三角形的性质与判定
5.★如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△A1B1C1相似的是( )
解析:因为△A1B1C1中有一个角是135°,选项中有135°角的三角形只有B,且满足两边成比例夹角相等.
B
命题点
图形的相似
第五讲 相似三角形
6.(2021·济南中考)如图,在△ABC中,∠ABC=90°,∠C=30°,以点A为圆心,以AB的长为半径作弧交AC于点D,连接BD,再分别以点B,D为圆心,大于 BD的长为半径作弧,两弧交于点P,作射线AP交BC于点E,连接DE,则下列结论中不正确的是( )
A.BE=DE B.DE垂直平分线段AC
C. D.BD2=BC·BE
C
解析:由题意知,AP为BD的垂直平分线,点E在AP上,则BE=DE,A选项正确;∵∠C=30°,∴∠BAC=60°.又∵AP为BD的垂直平分线,∴∠BAP=∠DAP=30°,∴AE=CE.又∵AB=AD= AC,∴AD=CD,∴ED⊥AC(三线合一),∴DE垂直平分线段AC,B选项正确;∵∠ABC=∠EDC=90°,∠C=∠C,∴△EDC∽△ABC.又∵DE=BE= C选项错误;∵∠AED=60°,∴∠EDB=30°=∠C.又∵∠DBE=∠CBD,∴△BED∽△BDC,∴ ,∴BD2=BC·BE,D选项正确.
命题点
图形的相似
第五讲 相似三角形
解析:∵△ABC与△DEF相似且面积之比为25∶16,∴△ABC与△DEF的相似比为5∶4,
∴△ABC的中线AM与△DEF的中线DN之比为5∶4.
5∶4
7.★若△ABC与△DEF相似且面积之比为25∶16,则△ABC的中线AM与△DEF的中线DN之比为 _________.
命题点
图形的相似
第五讲 相似三角形
8.★(2021·菏泽中考)如图,在△ABC中,AD⊥BC,垂足为D,AD=5,BC=10,四边形EFGH和四边形HGNM均为正方形,且点E,F,G,N,M都在△ABC的边上,那么△AEM与四边形BCME的面积比为 .
解析:∵四边形EFGH和四边形HGNM均为正方形,
∴EF=EH=HM,EM∥BC,∴△AEM∽△ABC,
∴ =,
∴ =,
∴EF=,∴EM=5.
∵△AEM∽△ABC,
∴ =( ) =,
∴S四边形BCME=S△ABC-S△AEM=3S△AEM,
∴△AEM与四边形BCME的面积比为1∶3.
1∶3
命题点
图形的相似
第五讲 相似三角形
9.如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.
求证:△ABE∽△ACD.
证明:
∵∠BAC=∠BDC,∠AOB=∠DOC,
∴∠ABE=∠ACD.
又∵∠BAC=∠DAE,
∴∠BAC+∠EAC=∠DAE+∠EAC,
∴∠EAB=∠DAC,
∴△ABE∽△ACD.
命题点
图形的相似
第五讲 相似三角形
10.(2021·牡丹江中考)Rt△ABC中,∠C=90°,AB=17,BC=8,矩形CDEF的另三个顶点D,E,F均在Rt△ABC的边上,且邻边之比为1∶2,画出符合题意的图形,并直接写出矩形周长的值.
命题点
图形的相似
第五讲 相似三角形
命题点
图形的相似
4
第五讲 相似三角形
命题点 相似三角形的应用
解析:由题意,得AB∥CD,
则∠BAE=∠C,∠B=∠CDE,∴△ABE∽△CDE,
∴=,
∴=,
∴CD=3米.
3
11.(2021·烟台中考)《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆AB,从木杆的顶端B观察井水水岸D,视线BD与井口的直径AC交于点E,如果测得AB=1米,AC=1.6米,AE=0.4米,那么CD为______米.
命题点
图形的相似
5
第五讲 相似三角形
命题点 位似图形的性质
12.(2021·重庆中考)如图,在平面直角坐标系中,将△OAB以原点O为位似中心放大后得到△OCD,若B(0,1),D(0,3),则△OAB与△OCD的相似比是( )
A.2∶1 B.1∶2 C.3∶1 D.1∶3
解析:∵B(0,1),D(0,3),
∴OB=1,OD=3.
∵将△OAB以原点O为位似中心放大后得到△OCD,
∴△OAB与△OCD的相似比是OB∶OD=1∶3.
D
命题点
图形的相似
第五讲 相似三角形
13.(2021·东营中考)如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )
A.-2a+3 B.-2a+1
C.-2a+2 D.-2a-2
解析:设点B′的横坐标为x,则B,C间的横坐标的长度为a-1,B′,C间的横坐标的长度为-x+1.∵△ABC放大到原来的2倍得到△A′B′C,∴2(a-1)=-x+1,解得x=-2a+3.
A
命题点
图形的相似
第五讲 相似三角形
14.★(2021·遂宁中考)如图,正方形ABCD中,点E是CD边上一点,连接BE,以BE为对角线作正方形BGEF,边EF与正方形ABCD的对角线BD相交于点H,连接AF,有以下五个结论:
①∠ABF=∠DBE;②△ABF∽△DBE;③AF⊥BD;④2BG2=BH·BD;
⑤若CE∶DE=1∶3,则BH∶DH=17∶16.
你认为其中正确是_________.(填写序号)
①②③④
命题点
图形的相似
第五讲 相似三角形
解析:∵四边形ABCD和四边形BGEF都是正方形,
∴△ABD和△FBE都是等腰直角三角形,
∴∠ABD=∠FBE=45°,
∴∠ABF=∠DBE,
∴①正确,符合题意;
∵△ABD∽△FBE,
∴ =,即 = .
又∵∠ABF=∠DBE,
∴△ABF∽△DBE,
∴②正确,符合题意;
∵△ABF∽△DBE,
∴∠FAB=∠BDE=45°,
∴AF⊥BD,
∴③正确,符合题意;
∵∠BEH=∠EDB=45°,∠EBH=∠DBE,∴△BEH∽△BDE,
∴ =,
∴BE =BD·BH.
∵BE= BG,
∴2BG =BH·BD,
∴④正确,符合题意;
∵CE∶DE=1∶3,
设CE=x,DE=3x,
∴BC=4x
.在Rt△BCE中,BE=x.
∵BE =BD·BH,
∴17x =4x·BH,
∴BH= x,∴DH= x,
∴BH∶DH=17∶15
∴⑤错误,不符合题意.故综上所述,正确的有①②③④.
命题点
图形的相似
模型
1
“A”字型相似三角形模型
1.如图1,在△ABC中,点D,E分别在AB,AC边上,且∠ABC=∠ADE,则有△ADE∽△ABC.
2.如图2,在△ABC中,点D,E分别在AB,AC边上,且∠ABC=∠AED,则有△AED∽△ABC.
命题点
解:(1)∵∠A=65°,∠B=40°,
∴∠C=180°-∠A-∠B=75°.
∵∠ADE=∠B,∠A=∠A,
∴△AED∽△ACB,
∴∠AED=∠C=75°.
(2)由(1)知,△AED∽△ACB,
∴ = ,
∴=,
∴BC= .
1.如图,在△ABC中,∠ADE=∠B,AD=7,AB=10,DE=6,∠A=65°,∠B=40°,
求:
(1)∠AED与∠C的度数;
(2)BC的长.
命题点
2.如图,在△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,设运动的时间为t(秒).
(1)用含t的代数式表示:AP= 厘米,AQ= 厘米;
(2)当以A,P,Q为顶点的三角形与△ABC相似时,运动时间是多少?
解:
(2)∵∠PAQ=∠BAC,
∴当△APQ∽△ABC时, =,
即=,解得t=;
当△APQ∽△ACB时,= ,
即 =
解得t=4.
∴当以A,P,Q为顶点的三角形与△ABC相似时,运动时间为 秒或4秒.
2t
16-3t
命题点
2
模型 “8”字型相似三角形模型
1.如图3,在△ABC中,点D,E分别在BA,CA边的延长线上,且∠ABC=∠ADE,则有△ADE∽△ABC.
2.如图4,在△ABC中,点D,E分别在BA,CA边的延长线上,且∠ABC=∠AED,则有△ADE∽△ACB.
命题点
3.如图,BD,AC相交于点P,连接BC,AD,且∠1=∠2,AD=3,DP=2,CP=1,求BC的长.
解:∵∠1=∠2,∠DPA=∠CPB,
∴△ADP∽△BCP,
∴==2.
∵AD=3,
∴BC=1.5.
命题点
4.如图,在四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
求证:(1)AC =AB·AD;
(2)△AFD∽△CFE.
证明:(1)∵AC平分∠DAB,
∴∠DAC=∠CAB.
又∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD∶AC=AC∶AB,
∴AC =AB·AD.
(2)∵E为AB的中点,
∴CE=BE=AE,
∴∠EAC=∠ECA.
∵∠DAC=∠CAB,
∴∠DAC=∠ECA.
又∵∠AFD=∠CFE,
∴△AFD∽△CFE.
命题点
模型
3
“母子”型相似三角形模型
1.如图5,在Rt△ABC中,∠BAC=90°,AD⊥BC,则有△ADB∽△CDA∽△CAB.
2.如图6,在△ABC中,点D是BC边上一点,且∠ABC=∠DAC,则有△DAC∽△ABC.
命题点
5.在Rt△ABC中,∠ACB=90°,D为AB边上一点,且CD⊥AB.
(1)求证:AC2=AB·AD;
(2)若△ABC为任意三角形,试问:在AB边上(不包括A,B两个顶
点)是否仍存在一点D,使AC2=AB·AD,若存在,请加以证明;
若不存在,请说明理由.
解:(1)证明:∵CD⊥AB,∴∠ADC=∠ACB=90°.
又∵∠A=∠A,
∴△ACD∽△ABC,
∴=,
∴AC =AB·AD.
(2)存在.理由如下:
如图,过点C作∠ACD=∠B交AB于点D,
则AC =AB·AD,
证明:∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC,
∴ =,
∴AC =AB·AD.
命题点
6.如图,在△ABC中,BD⊥AC于点D,DE⊥AB于点E,BD·DE=BE·CD.
(1)求证:△BCD∽△BDE;
(2)若BC=10,AD=6,求AE的长.
解:(1)证明:∵BD⊥AC,DE⊥AB,
∴∠BDC=∠BED=90°.
又∵BD·DE=BE·CD,
∴=,
∴△BCD∽△BDE.
∴=,
∴=,
∴BE=,
∴AE=BA-BE=10-=.
(2)∵△BCD∽△BDE,∴∠EBD=∠DBC.
又∵BD⊥AC,
∴CD=AD=6,BA=BC=10.
∵BD⊥AC,
∴BD==8.
∵△BCD∽△BDE,
命题点
7.如图,在 ABCD中,∠BAD的平分线交边BC于点E,交DC的延长线于点F,点G在AE上,连接GD,∠GDF=∠F.
(1)求证:AD2=DG·AF;
(2)连接BG,如果BG⊥AE,且AB=6,AD=9,求AF的长.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DF,AD∥BC,∴∠BAF=∠F.
∵AE平分∠BAD,∴∠BAF=∠DAF=∠F,
∴AD=DF.
∵∠GDF=∠F,∴∠GDF=∠DAF.
又∵∠F=∠F,∴△GDF∽△DAF,
∴=,
∴AD =DG·AF.
(2)∵AF平分∠BAD,
∴∠BAE=∠DAF.
∵AD∥BC,∴∠BEA=∠DAF,
∴∠BEA=∠BAE,
∴BA=BE=6.
又∵BG⊥AE,∴AG=GE.
∵∠BEA=∠CEF,∴∠CEF=∠F.
∵AD=BC=9,
∴CF=EC=3,DF=AD=9.
∵AD∥BC,∴==,即AG=GE=EF=3
∵∠F=∠GDF,∴DG=GF=AF.
∵AD =DG·AF,∴AF =81,
∴AF=.
命题点
8.如图1,△ABC内接于⊙O,点D是线段 的中点,且与点C位于AB的异侧,CD交AB于点E.
(1)求证:△ADE∽△CDA.
(2)如图2,若⊙O的直径AB=4,CE=2,求AD和CD的长.
解:
(1)∵点D是 的中点,
∴∠ACD=∠BAD.
又∵∠ADE=∠CDA,
∴△ADE∽△CDA.
(2)如图,连接BD.
∵点D是 的中点,
∴AD=BD.
∵AB是⊙O的直径,∴∠ADB=90°,
∴△ADB为等腰直角三角形,
∴AD===4.
由(1)得△ADE∽△CDA,
∴=,即AD =CD·ED,
∴(4) =CD(CD-2),
∴CD=8.
命题点
模型
4
旋转型相似三角形模型
等角的顶点重合且等角的两边对应成比例的两个三角形旋转——相似三角形,如图:
总结:=,∠CAE=∠BAF→△ACE∽△ABF.
命题点
9.如图,已知四边形ABCD和EFCG均为正方形,点E在△ABC内,∠CAE+∠CBE=90°.
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求BF和CE的长.
解:(1)证明:∵四边形ABCD和EFCG均为正方形,
∴==.
又∵∠ACE+∠BCE=∠BCF+∠BCE=45°,
∴∠ACE=∠BCF,∴△CAE∽△CBF.
(2)∵△CAE∽△CBF,
∴∠CAE=∠CBF,==,
∴BF= AE=.
∴∠CBF+∠CBE=∠CAE+∠CBE=90°,即∠EBF=90°.
∴EF2=BE2+BF2=12+()2=3,则EF=.
∴CE=EF=.
命题点
10.如图,在△ABC中,AB=AC,△ADE∽△ABC,连接BD,CE.
(1)判断BD与CE的数量关系,并证明你的结论;
(2)若AB=2√3,AD=4,∠BAC=120°,∠CAD=30°.求BD的长.
(1)BD=CE.
证明:∵△ADE∽△ABC,AB=AC,
∴∠BAC=∠DAE,AD=AE,
∴∠BAC+∠CAD=∠CAD+∠DAE,
即∠BAD=∠CAE.
在△ABD与△ACE中,
∴△ABD≌△ACE(SAS),
∴BD=CE.
(2)如图,过点D作DH⊥BA交BA的延长线于点H.
∵∠BAD=∠BAC+∠CAD=150°,
∴∠DAH=30°.
∵∠H=90°,AD=4,
∴DH=2,AH=2,
∴BH=AH+AB=4.
在Rt△BDH中,
BD===2.
命题点
11.小华和小芳对等腰直角三角形的旋转变换进行研究.如图1,已知△ABC和△ADE均为等腰直角三角形,点D,E分别在线段AB,AC上,且∠C=∠AED=90°.
(1)观察猜想
小华将△ADE绕点A逆时针旋转,连接BD,CE,如图2,当BD的延长线恰好经过点E时,
①的值为 ;
②∠BEC的度数为 度;
(2)类比探究
如图3,小芳在小华的基础上,继续旋转△ADE,连接BD,CE,设BD的延长线交CE于点F,请求出的值及∠BFC的度数.
(3)拓展延伸
若AE=DE=,AC=BC=,当CE所在的直线垂直于AD时,请你直接写出BD的长.
45
命题点
(1)如图1,设AC交BE于点O.
∵△ADE,△ABC都是等腰直角三角形,
∴∠EAD=∠CAB=45°,AD=AE,AB=AC,
∴∠EAC=∠DAB,==,
∴△DAB∽△EAC,
∴==,∠ABO=∠ACE.
∵∠AOB=∠EOC,
∴∠BEC=∠BAC=45°.
故答案为:① . ②45.
(2)如图2,设AC交BF于点O.
∵△ADE,△ABC都是等腰直角三角形,
∴∠EAD=∠CAB=45°,AD=AE,AB=AC,
∴∠EAC=∠DAB,==
∴△DAB∽△EAC,
∴ = = ,∠ABD=∠ACE.
∵∠AOB=∠FOC,
∴∠BFC=∠BAC=45°.
命题点
(3)如图3,当CE⊥AD于点O时,
∵AE=DE=,∠AED=90°,
∴AD=AE=2.
∵EO⊥AD,
∴OD=OA=OE=1,
∴OC==3,
∴CE=OE+OC=4.
∵BD=CE,∴BD=4;
如图4,当CE⊥AD交CE的延长线于点O时,
同理可得OD=OA=OE=1,OC=3,
∴CE=OC-OE=2,
∴BD=CE=2.
综上所述,BD的长为4或2.
命题点
模型
5
“赵爽弦图”衍生的相似三角形模型
一线三等角是有三个相等的角的顶点在同一条直线上构成的图形,这三个相等的角可以在同侧(在同侧时,三个等角可以是直角(如图①),也可以是钝角(如图②)或锐角(如图③、图④),也可以在异侧(如图⑤).“一线三等角”模型也可称为“K字型”.
注:这些模型常用来证明三角形的全等或相似.
命题点
12.如图,∠ACB=90°,CA=BC,AD⊥CE,BE⊥CE,垂足分别是点D,E,AD=3,BE=1,则DE的长是( )
A.B.2 C.2 D.
解析:∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=90°,
∴∠EBC+∠BCE=90°.
∵∠BCE+∠DCA=90°,
∴∠EBC=∠DCA.
在△CEB和△ADC中
∴△CEB≌△ADC(AAS),
∴BE=CD=1,CE=AD=3.
∴DE=CE-CD=2.
B
命题点
13.如图,AB,CD都是BD的垂线,AB=4,CD=6,BD=14,P是BD上一点,连接AP,CP,所得两个三角形相似,则BP的长是 .
解析:设BP=x,
则PD=14-x.
当△ABP∽△PDC时,= ,即 =,
解得x1=2,x2=12;
当△ABP∽△CDP时,
= ,即 = ,
解得x= .
综上所述,当所得两个三角形相似时,
BP的长为2或12或 .
2或12或
命题点
14.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足
为F,连接DF,求tan∠CAD的值.
解:如图,设AD=2a.
∵E是AD的中点,
∴AE=a.
∵四边形ABCD为矩形,
∴AB=CD,∠BAD=∠ADC=90°,
∴∠1+∠2=90°.
∵BE⊥AC,∴∠2+∠3=90°,
∴∠1=∠3.
∴△BAE∽△ADC.
∴=,即=.
又∵BA=DC,
∴DC=a.
∴tan∠CAD= ==.
命题点
15.如图,在矩形ABCD中,已知AD>AB.在边AD上取点E,连接CE.过点E作EF⊥CE,与边AB的延长线交于点F.
(1)求证:△AEF∽△DCE;
(2)若AB=3,AE=4,DE=6,求线段BF的长.
解:(1)证明:∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴∠AEF+∠F=90°.
∵EF⊥CE,
∴∠CED+∠AEF=180°-90°=90°,
∴∠CED=∠F.
又∵∠A=∠D=90°,
∴△AEF∽△DCE.
(2)∵△AEF∽△DCE,
∴=.
∵AB=CD=3,AE=4,DE=6,
∴ = ,
∴BF=5.
16.如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,D是BC边上的一个动点(不与点B,C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围.
解:(1)证明:
∵△ABC是等腰三角形,∠BAC=120°,
∴∠B=∠C=30°,
∴∠B=∠ADE.
∵∠ADC=∠ADE+∠EDC=∠B+∠DAB.
∴∠DAB=∠EDC.
∴△ABD∽△DCE.
(2)如图,过点A作AF⊥BC于点F,则∠AFB=90°,BF=CF.
∵AB=2,∠B=30°,
∴AF=1,BF=.
∴BC=2BF=2.
∵△ABD∽△DCE.
∴=,即
化简,得y= x - x+2(0
1.重点
2.考点
3.命题点
1.了解比例的基本性质、线段的比、成比例的线段;通过建筑、艺术上的实例了解黄金分割.
2.掌握基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
3.了解相似三角形的性质定理和判定定理.
4.通过具体实例认识图形的相似,了解相似多边形和相似比.
5.会利用图形的相似解决一些简单的实际问题.
6.了解相似三角形判定定理的证明.
图形的相似
重点
相似三角形
比例线段
比例性质
平行线分线段成比例
第五讲 相似三角形
交叉相乘积相等:
①
=
(abcd≠0)
(1)基本事实:两条直线被一组平行线所截,所,得的线段成比例.如图1,图2,当l1∥l2∥,l3时,
(2)推论:平行于三角形一边的直线截其他两边(或两边的延长,线),所得的线段成比例.如图3,当DE∥BC时,有=
ad=bc
重点
图形的相似
相似三角形
比例线段
相似三角形的性质及判定
第五讲 相似三角形
1.性质
2.判定
(1)相似三角形对应角② ,对应边③ .
(2)相似三角形对应线段(边、高、④ 、角平分线)的比等于相似比.
(3)相似三角形周长的比等于相似比,面积的比等于 ⑤
预备定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
一般三角形
(1)两角分别⑥ 的两个三角形相似.
(2)三边⑦ 的两个三角形相似.
(3)两边⑧ 且⑨ 的两个三角形相似.
直角三角形
(1)一组⑩ 对应相等,两三角形相似.
(2)两条边对应成比例,两三角形相似.
相等
成比例
中线
相似比的平方
相等
成比例
成比例
夹角相等
锐角
重点
图形的相似
发
相似三角形
相似多边形的性质及判定
第五讲 相似三角形
1.性质
2.判定
(1)对应角相等,对应边 .
(2)对应边的比、周长的比都等于 ,面积的比等于 .
(1)对应角相等,对应边成比例的多边形是相似多边形.
(2)所有对应边成比例,那么这两个多边形是相似多边形.
相似三角形的实际运用
1.步骤
2.常考类型
(1)将实际问题转化为相似三角形问题.
(2)找出一对相似三角形.
(3)根据相似三角形的性质,表示出相应的量,并求解.
(1)利用光的反射定律求物体的高度.
(2)利用影子计算建筑物的高度(同一时刻,物高与影长成正比例,有:=.
(3)构造相似三角形计算不能直接测量的物体的高度(宽度).
成比例
相似比
相似比的平方
重点
图形的相似
相似三角形
图形的位似
第五讲 相似三角形
定义 :如果两个图形不仅是相似图形,而且每组对应点所在直线都经过同一点,那么这两个图,形叫做位似图形,这个点叫做位似中心
2.性质
3.位似变换与坐标的关系:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标等于k 或
(1)位似图形上的任意一对对应点到位似中心的距离之比等于 ,面积比等,于相似比的平方.
(2)位似图形对应点的连线或延长线相交于同一点.
(3)位似图形对应边 且成比例.
(4)位似图形对应角 .
相似比
平行(或共线)
相等
-k
重点
图形的相似
第五讲 相似三角形
一、相似三角形的判定
例1.如图,在△ABC中,点P在边AB上.
(1)可以添加条件 ,使得△APC∽△ACB,依据是 ;
(2)可以添加条件 ,使得△APC∽△ACB,依据是 ;
(3)可以添加条件 ,使得△APC∽△ACB;依据是
(4)如果∠ACP=∠B,且AP=2,BP=3,则AC的长为.
∠ACP=∠B
两角分别相等的两个三角形相似
∠APC=∠ACB
两角分别相等的两个三角形相似
AC =AP·AB
两边成比例且夹角相等的两个三角形相似
考点
图形的相似
第五讲 相似三角形
练习1.如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.图中相似三角形有
解析:∵∠BAD=∠CAE,∠BAD+∠DAC=∠CAE+∠DAC,即∠BAC=∠DAE.
又∵∠ABC=∠ADE,
∴△ABC∽△ADE.∵△ABC∽△ADE,
∴=
又∵∠BAD=∠CAE,
∴△ABD∽△ACE.
△ABC∽△ADE,△ABD∽△ACE.
考点
图形的相似
第五讲 相似三角形
二、相似三角形的判定和性质
例2.(2020·杭州中考)如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC;
(2)设=,
①若BC=12,求线段BE的长;
②若△EFC的面积是20,求△ABC的面积.
考点
图形的相似
第五讲 相似三角形
解:(1)证明:∵DE∥AC,
∴∠DEB=∠FCE.
∵EF∥AB,
∴∠DBE=∠FEC,
∴△BDE∽△EFC.
(2)①∵EF∥AB,
∴= =.
∵EC=BC-BE=12-BE,
∴ =,解得BE=4.
②∵=,
∴=.
∵EF∥AB,
∴△EFC∽△BAC,
=() =() =
∴S△ABC= S△EFC= ×20=45.
考点
图形的相似
第五讲 相似三角形
练习2.如图,AB与CD相交于点O,△OBD∽△OAC,=,OB=6,S△AOC=50,求AO的长及△BOD的面积.
解:∵△OBD∽△OAC,∴= = .
∵OB=6,∴AO=10.
∵=,
∵S△AOC=50,
∴S△BOD=18.
考点
图形的相似
第五讲 相似三角形
练习3.如图,在△ABC中,BC=120,高AD=60,正方形EFGH一边在BC上,点E,F分别在AB,AC上,AD交EF于点N,求AN的长.
解:设正方形EFGH的边长EF=EH=x.
∵四边形EFGH是正方形,
∴∠HEF=∠EHG=90°,EF∥BC,
∴△AEF∽△ABC.
∵AD是△ABC的高,
∴∠HDN=90°,
∴四边形EHDN是矩形,
∴DN=EH=x.
∵△AEF∽△ABC,
∴=.
∵BC=120,AD=60,
∴AN=60-x,
∴ =,解得x=40,
∴AN=60-x=60-40=20.
考点
图形的相似
第五讲 相似三角形
命题点 成比例的线段
1.如果=,那么的值是( )
A.3 B.-3 C. D.-
解析:∵ = ,∴ b=2a ∴原式= =
B
命题点
图形的相似
第五讲 相似三角形
解析:设 == =k,则x=2k,y=3k,z=4k,
∴=== .
2.(2021·大庆中考)已知,则=___.
命题点
图形的相似
2
第五讲 相似三角形
命题点 平行线分线段成比例
C
3.(2021·淄博中考)如图,AB,CD相交于点E,且AC∥EF∥DB,点C,F,B在同一条直线上.已知AC=p,EF=r,DB=q,则p,q,r之间满足的数量关系式是( )
命题点
图形的相似
第五讲 相似三角形
4.★如图,在△ABC中,点D在BC边上,连接AD,点E在AC边上,过点E作EF∥BC,交AD于点F,过点E作EG∥AB,交BC于点G,则下列式子一定正确的是( )
A.= B.=
C.= D.=
解析:∵EF∥BC,
∴= .
∵EG∥AB,
∴ =
C
命题点
图形的相似
3
第五讲 相似三角形
命题点 相似三角形的性质与判定
5.★如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△A1B1C1相似的是( )
解析:因为△A1B1C1中有一个角是135°,选项中有135°角的三角形只有B,且满足两边成比例夹角相等.
B
命题点
图形的相似
第五讲 相似三角形
6.(2021·济南中考)如图,在△ABC中,∠ABC=90°,∠C=30°,以点A为圆心,以AB的长为半径作弧交AC于点D,连接BD,再分别以点B,D为圆心,大于 BD的长为半径作弧,两弧交于点P,作射线AP交BC于点E,连接DE,则下列结论中不正确的是( )
A.BE=DE B.DE垂直平分线段AC
C. D.BD2=BC·BE
C
解析:由题意知,AP为BD的垂直平分线,点E在AP上,则BE=DE,A选项正确;∵∠C=30°,∴∠BAC=60°.又∵AP为BD的垂直平分线,∴∠BAP=∠DAP=30°,∴AE=CE.又∵AB=AD= AC,∴AD=CD,∴ED⊥AC(三线合一),∴DE垂直平分线段AC,B选项正确;∵∠ABC=∠EDC=90°,∠C=∠C,∴△EDC∽△ABC.又∵DE=BE= C选项错误;∵∠AED=60°,∴∠EDB=30°=∠C.又∵∠DBE=∠CBD,∴△BED∽△BDC,∴ ,∴BD2=BC·BE,D选项正确.
命题点
图形的相似
第五讲 相似三角形
解析:∵△ABC与△DEF相似且面积之比为25∶16,∴△ABC与△DEF的相似比为5∶4,
∴△ABC的中线AM与△DEF的中线DN之比为5∶4.
5∶4
7.★若△ABC与△DEF相似且面积之比为25∶16,则△ABC的中线AM与△DEF的中线DN之比为 _________.
命题点
图形的相似
第五讲 相似三角形
8.★(2021·菏泽中考)如图,在△ABC中,AD⊥BC,垂足为D,AD=5,BC=10,四边形EFGH和四边形HGNM均为正方形,且点E,F,G,N,M都在△ABC的边上,那么△AEM与四边形BCME的面积比为 .
解析:∵四边形EFGH和四边形HGNM均为正方形,
∴EF=EH=HM,EM∥BC,∴△AEM∽△ABC,
∴ =,
∴ =,
∴EF=,∴EM=5.
∵△AEM∽△ABC,
∴ =( ) =,
∴S四边形BCME=S△ABC-S△AEM=3S△AEM,
∴△AEM与四边形BCME的面积比为1∶3.
1∶3
命题点
图形的相似
第五讲 相似三角形
9.如图,点E是四边形ABCD的对角线BD上一点,且∠BAC=∠BDC=∠DAE.
求证:△ABE∽△ACD.
证明:
∵∠BAC=∠BDC,∠AOB=∠DOC,
∴∠ABE=∠ACD.
又∵∠BAC=∠DAE,
∴∠BAC+∠EAC=∠DAE+∠EAC,
∴∠EAB=∠DAC,
∴△ABE∽△ACD.
命题点
图形的相似
第五讲 相似三角形
10.(2021·牡丹江中考)Rt△ABC中,∠C=90°,AB=17,BC=8,矩形CDEF的另三个顶点D,E,F均在Rt△ABC的边上,且邻边之比为1∶2,画出符合题意的图形,并直接写出矩形周长的值.
命题点
图形的相似
第五讲 相似三角形
命题点
图形的相似
4
第五讲 相似三角形
命题点 相似三角形的应用
解析:由题意,得AB∥CD,
则∠BAE=∠C,∠B=∠CDE,∴△ABE∽△CDE,
∴=,
∴=,
∴CD=3米.
3
11.(2021·烟台中考)《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆AB,从木杆的顶端B观察井水水岸D,视线BD与井口的直径AC交于点E,如果测得AB=1米,AC=1.6米,AE=0.4米,那么CD为______米.
命题点
图形的相似
5
第五讲 相似三角形
命题点 位似图形的性质
12.(2021·重庆中考)如图,在平面直角坐标系中,将△OAB以原点O为位似中心放大后得到△OCD,若B(0,1),D(0,3),则△OAB与△OCD的相似比是( )
A.2∶1 B.1∶2 C.3∶1 D.1∶3
解析:∵B(0,1),D(0,3),
∴OB=1,OD=3.
∵将△OAB以原点O为位似中心放大后得到△OCD,
∴△OAB与△OCD的相似比是OB∶OD=1∶3.
D
命题点
图形的相似
第五讲 相似三角形
13.(2021·东营中考)如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点B′的横坐标是( )
A.-2a+3 B.-2a+1
C.-2a+2 D.-2a-2
解析:设点B′的横坐标为x,则B,C间的横坐标的长度为a-1,B′,C间的横坐标的长度为-x+1.∵△ABC放大到原来的2倍得到△A′B′C,∴2(a-1)=-x+1,解得x=-2a+3.
A
命题点
图形的相似
第五讲 相似三角形
14.★(2021·遂宁中考)如图,正方形ABCD中,点E是CD边上一点,连接BE,以BE为对角线作正方形BGEF,边EF与正方形ABCD的对角线BD相交于点H,连接AF,有以下五个结论:
①∠ABF=∠DBE;②△ABF∽△DBE;③AF⊥BD;④2BG2=BH·BD;
⑤若CE∶DE=1∶3,则BH∶DH=17∶16.
你认为其中正确是_________.(填写序号)
①②③④
命题点
图形的相似
第五讲 相似三角形
解析:∵四边形ABCD和四边形BGEF都是正方形,
∴△ABD和△FBE都是等腰直角三角形,
∴∠ABD=∠FBE=45°,
∴∠ABF=∠DBE,
∴①正确,符合题意;
∵△ABD∽△FBE,
∴ =,即 = .
又∵∠ABF=∠DBE,
∴△ABF∽△DBE,
∴②正确,符合题意;
∵△ABF∽△DBE,
∴∠FAB=∠BDE=45°,
∴AF⊥BD,
∴③正确,符合题意;
∵∠BEH=∠EDB=45°,∠EBH=∠DBE,∴△BEH∽△BDE,
∴ =,
∴BE =BD·BH.
∵BE= BG,
∴2BG =BH·BD,
∴④正确,符合题意;
∵CE∶DE=1∶3,
设CE=x,DE=3x,
∴BC=4x
.在Rt△BCE中,BE=x.
∵BE =BD·BH,
∴17x =4x·BH,
∴BH= x,∴DH= x,
∴BH∶DH=17∶15
∴⑤错误,不符合题意.故综上所述,正确的有①②③④.
命题点
图形的相似
模型
1
“A”字型相似三角形模型
1.如图1,在△ABC中,点D,E分别在AB,AC边上,且∠ABC=∠ADE,则有△ADE∽△ABC.
2.如图2,在△ABC中,点D,E分别在AB,AC边上,且∠ABC=∠AED,则有△AED∽△ABC.
命题点
解:(1)∵∠A=65°,∠B=40°,
∴∠C=180°-∠A-∠B=75°.
∵∠ADE=∠B,∠A=∠A,
∴△AED∽△ACB,
∴∠AED=∠C=75°.
(2)由(1)知,△AED∽△ACB,
∴ = ,
∴=,
∴BC= .
1.如图,在△ABC中,∠ADE=∠B,AD=7,AB=10,DE=6,∠A=65°,∠B=40°,
求:
(1)∠AED与∠C的度数;
(2)BC的长.
命题点
2.如图,在△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,设运动的时间为t(秒).
(1)用含t的代数式表示:AP= 厘米,AQ= 厘米;
(2)当以A,P,Q为顶点的三角形与△ABC相似时,运动时间是多少?
解:
(2)∵∠PAQ=∠BAC,
∴当△APQ∽△ABC时, =,
即=,解得t=;
当△APQ∽△ACB时,= ,
即 =
解得t=4.
∴当以A,P,Q为顶点的三角形与△ABC相似时,运动时间为 秒或4秒.
2t
16-3t
命题点
2
模型 “8”字型相似三角形模型
1.如图3,在△ABC中,点D,E分别在BA,CA边的延长线上,且∠ABC=∠ADE,则有△ADE∽△ABC.
2.如图4,在△ABC中,点D,E分别在BA,CA边的延长线上,且∠ABC=∠AED,则有△ADE∽△ACB.
命题点
3.如图,BD,AC相交于点P,连接BC,AD,且∠1=∠2,AD=3,DP=2,CP=1,求BC的长.
解:∵∠1=∠2,∠DPA=∠CPB,
∴△ADP∽△BCP,
∴==2.
∵AD=3,
∴BC=1.5.
命题点
4.如图,在四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
求证:(1)AC =AB·AD;
(2)△AFD∽△CFE.
证明:(1)∵AC平分∠DAB,
∴∠DAC=∠CAB.
又∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD∶AC=AC∶AB,
∴AC =AB·AD.
(2)∵E为AB的中点,
∴CE=BE=AE,
∴∠EAC=∠ECA.
∵∠DAC=∠CAB,
∴∠DAC=∠ECA.
又∵∠AFD=∠CFE,
∴△AFD∽△CFE.
命题点
模型
3
“母子”型相似三角形模型
1.如图5,在Rt△ABC中,∠BAC=90°,AD⊥BC,则有△ADB∽△CDA∽△CAB.
2.如图6,在△ABC中,点D是BC边上一点,且∠ABC=∠DAC,则有△DAC∽△ABC.
命题点
5.在Rt△ABC中,∠ACB=90°,D为AB边上一点,且CD⊥AB.
(1)求证:AC2=AB·AD;
(2)若△ABC为任意三角形,试问:在AB边上(不包括A,B两个顶
点)是否仍存在一点D,使AC2=AB·AD,若存在,请加以证明;
若不存在,请说明理由.
解:(1)证明:∵CD⊥AB,∴∠ADC=∠ACB=90°.
又∵∠A=∠A,
∴△ACD∽△ABC,
∴=,
∴AC =AB·AD.
(2)存在.理由如下:
如图,过点C作∠ACD=∠B交AB于点D,
则AC =AB·AD,
证明:∵∠ACD=∠B,∠A=∠A,
∴△ACD∽△ABC,
∴ =,
∴AC =AB·AD.
命题点
6.如图,在△ABC中,BD⊥AC于点D,DE⊥AB于点E,BD·DE=BE·CD.
(1)求证:△BCD∽△BDE;
(2)若BC=10,AD=6,求AE的长.
解:(1)证明:∵BD⊥AC,DE⊥AB,
∴∠BDC=∠BED=90°.
又∵BD·DE=BE·CD,
∴=,
∴△BCD∽△BDE.
∴=,
∴=,
∴BE=,
∴AE=BA-BE=10-=.
(2)∵△BCD∽△BDE,∴∠EBD=∠DBC.
又∵BD⊥AC,
∴CD=AD=6,BA=BC=10.
∵BD⊥AC,
∴BD==8.
∵△BCD∽△BDE,
命题点
7.如图,在 ABCD中,∠BAD的平分线交边BC于点E,交DC的延长线于点F,点G在AE上,连接GD,∠GDF=∠F.
(1)求证:AD2=DG·AF;
(2)连接BG,如果BG⊥AE,且AB=6,AD=9,求AF的长.
解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DF,AD∥BC,∴∠BAF=∠F.
∵AE平分∠BAD,∴∠BAF=∠DAF=∠F,
∴AD=DF.
∵∠GDF=∠F,∴∠GDF=∠DAF.
又∵∠F=∠F,∴△GDF∽△DAF,
∴=,
∴AD =DG·AF.
(2)∵AF平分∠BAD,
∴∠BAE=∠DAF.
∵AD∥BC,∴∠BEA=∠DAF,
∴∠BEA=∠BAE,
∴BA=BE=6.
又∵BG⊥AE,∴AG=GE.
∵∠BEA=∠CEF,∴∠CEF=∠F.
∵AD=BC=9,
∴CF=EC=3,DF=AD=9.
∵AD∥BC,∴==,即AG=GE=EF=3
∵∠F=∠GDF,∴DG=GF=AF.
∵AD =DG·AF,∴AF =81,
∴AF=.
命题点
8.如图1,△ABC内接于⊙O,点D是线段 的中点,且与点C位于AB的异侧,CD交AB于点E.
(1)求证:△ADE∽△CDA.
(2)如图2,若⊙O的直径AB=4,CE=2,求AD和CD的长.
解:
(1)∵点D是 的中点,
∴∠ACD=∠BAD.
又∵∠ADE=∠CDA,
∴△ADE∽△CDA.
(2)如图,连接BD.
∵点D是 的中点,
∴AD=BD.
∵AB是⊙O的直径,∴∠ADB=90°,
∴△ADB为等腰直角三角形,
∴AD===4.
由(1)得△ADE∽△CDA,
∴=,即AD =CD·ED,
∴(4) =CD(CD-2),
∴CD=8.
命题点
模型
4
旋转型相似三角形模型
等角的顶点重合且等角的两边对应成比例的两个三角形旋转——相似三角形,如图:
总结:=,∠CAE=∠BAF→△ACE∽△ABF.
命题点
9.如图,已知四边形ABCD和EFCG均为正方形,点E在△ABC内,∠CAE+∠CBE=90°.
(1)求证:△CAE∽△CBF;
(2)若BE=1,AE=2,求BF和CE的长.
解:(1)证明:∵四边形ABCD和EFCG均为正方形,
∴==.
又∵∠ACE+∠BCE=∠BCF+∠BCE=45°,
∴∠ACE=∠BCF,∴△CAE∽△CBF.
(2)∵△CAE∽△CBF,
∴∠CAE=∠CBF,==,
∴BF= AE=.
∴∠CBF+∠CBE=∠CAE+∠CBE=90°,即∠EBF=90°.
∴EF2=BE2+BF2=12+()2=3,则EF=.
∴CE=EF=.
命题点
10.如图,在△ABC中,AB=AC,△ADE∽△ABC,连接BD,CE.
(1)判断BD与CE的数量关系,并证明你的结论;
(2)若AB=2√3,AD=4,∠BAC=120°,∠CAD=30°.求BD的长.
(1)BD=CE.
证明:∵△ADE∽△ABC,AB=AC,
∴∠BAC=∠DAE,AD=AE,
∴∠BAC+∠CAD=∠CAD+∠DAE,
即∠BAD=∠CAE.
在△ABD与△ACE中,
∴△ABD≌△ACE(SAS),
∴BD=CE.
(2)如图,过点D作DH⊥BA交BA的延长线于点H.
∵∠BAD=∠BAC+∠CAD=150°,
∴∠DAH=30°.
∵∠H=90°,AD=4,
∴DH=2,AH=2,
∴BH=AH+AB=4.
在Rt△BDH中,
BD===2.
命题点
11.小华和小芳对等腰直角三角形的旋转变换进行研究.如图1,已知△ABC和△ADE均为等腰直角三角形,点D,E分别在线段AB,AC上,且∠C=∠AED=90°.
(1)观察猜想
小华将△ADE绕点A逆时针旋转,连接BD,CE,如图2,当BD的延长线恰好经过点E时,
①的值为 ;
②∠BEC的度数为 度;
(2)类比探究
如图3,小芳在小华的基础上,继续旋转△ADE,连接BD,CE,设BD的延长线交CE于点F,请求出的值及∠BFC的度数.
(3)拓展延伸
若AE=DE=,AC=BC=,当CE所在的直线垂直于AD时,请你直接写出BD的长.
45
命题点
(1)如图1,设AC交BE于点O.
∵△ADE,△ABC都是等腰直角三角形,
∴∠EAD=∠CAB=45°,AD=AE,AB=AC,
∴∠EAC=∠DAB,==,
∴△DAB∽△EAC,
∴==,∠ABO=∠ACE.
∵∠AOB=∠EOC,
∴∠BEC=∠BAC=45°.
故答案为:① . ②45.
(2)如图2,设AC交BF于点O.
∵△ADE,△ABC都是等腰直角三角形,
∴∠EAD=∠CAB=45°,AD=AE,AB=AC,
∴∠EAC=∠DAB,==
∴△DAB∽△EAC,
∴ = = ,∠ABD=∠ACE.
∵∠AOB=∠FOC,
∴∠BFC=∠BAC=45°.
命题点
(3)如图3,当CE⊥AD于点O时,
∵AE=DE=,∠AED=90°,
∴AD=AE=2.
∵EO⊥AD,
∴OD=OA=OE=1,
∴OC==3,
∴CE=OE+OC=4.
∵BD=CE,∴BD=4;
如图4,当CE⊥AD交CE的延长线于点O时,
同理可得OD=OA=OE=1,OC=3,
∴CE=OC-OE=2,
∴BD=CE=2.
综上所述,BD的长为4或2.
命题点
模型
5
“赵爽弦图”衍生的相似三角形模型
一线三等角是有三个相等的角的顶点在同一条直线上构成的图形,这三个相等的角可以在同侧(在同侧时,三个等角可以是直角(如图①),也可以是钝角(如图②)或锐角(如图③、图④),也可以在异侧(如图⑤).“一线三等角”模型也可称为“K字型”.
注:这些模型常用来证明三角形的全等或相似.
命题点
12.如图,∠ACB=90°,CA=BC,AD⊥CE,BE⊥CE,垂足分别是点D,E,AD=3,BE=1,则DE的长是( )
A.B.2 C.2 D.
解析:∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=90°,
∴∠EBC+∠BCE=90°.
∵∠BCE+∠DCA=90°,
∴∠EBC=∠DCA.
在△CEB和△ADC中
∴△CEB≌△ADC(AAS),
∴BE=CD=1,CE=AD=3.
∴DE=CE-CD=2.
B
命题点
13.如图,AB,CD都是BD的垂线,AB=4,CD=6,BD=14,P是BD上一点,连接AP,CP,所得两个三角形相似,则BP的长是 .
解析:设BP=x,
则PD=14-x.
当△ABP∽△PDC时,= ,即 =,
解得x1=2,x2=12;
当△ABP∽△CDP时,
= ,即 = ,
解得x= .
综上所述,当所得两个三角形相似时,
BP的长为2或12或 .
2或12或
命题点
14.如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足
为F,连接DF,求tan∠CAD的值.
解:如图,设AD=2a.
∵E是AD的中点,
∴AE=a.
∵四边形ABCD为矩形,
∴AB=CD,∠BAD=∠ADC=90°,
∴∠1+∠2=90°.
∵BE⊥AC,∴∠2+∠3=90°,
∴∠1=∠3.
∴△BAE∽△ADC.
∴=,即=.
又∵BA=DC,
∴DC=a.
∴tan∠CAD= ==.
命题点
15.如图,在矩形ABCD中,已知AD>AB.在边AD上取点E,连接CE.过点E作EF⊥CE,与边AB的延长线交于点F.
(1)求证:△AEF∽△DCE;
(2)若AB=3,AE=4,DE=6,求线段BF的长.
解:(1)证明:∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴∠AEF+∠F=90°.
∵EF⊥CE,
∴∠CED+∠AEF=180°-90°=90°,
∴∠CED=∠F.
又∵∠A=∠D=90°,
∴△AEF∽△DCE.
(2)∵△AEF∽△DCE,
∴=.
∵AB=CD=3,AE=4,DE=6,
∴ = ,
∴BF=5.
16.如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,D是BC边上的一个动点(不与点B,C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围.
解:(1)证明:
∵△ABC是等腰三角形,∠BAC=120°,
∴∠B=∠C=30°,
∴∠B=∠ADE.
∵∠ADC=∠ADE+∠EDC=∠B+∠DAB.
∴∠DAB=∠EDC.
∴△ABD∽△DCE.
(2)如图,过点A作AF⊥BC于点F,则∠AFB=90°,BF=CF.
∵AB=2,∠B=30°,
∴AF=1,BF=.
∴BC=2BF=2.
∵△ABD∽△DCE.
∴=,即
化简,得y= x - x+2(0
