【大单元教学】鲁教版2023年八年级大单元 第六章 特殊的平行四边形 课件(32张PPT)
文档属性
| 名称 | 【大单元教学】鲁教版2023年八年级大单元 第六章 特殊的平行四边形 课件(32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 11:22:32 | ||
图片预览









文档简介
(共32张PPT)
1.重点
2.考点
3.命题点
1.理解矩形的概念.
2.探索并证明矩形的性质定理及判定定理.
3.理解菱形的概念.
4.探索并证明菱形的性质定理及判定定理.
5.理解正方形的概念,以及平行四边形、矩形、菱形、正方形之间的关系.
6.探索并证明正方形的性质定理及判定定理.
重点
矩形、菱形和正方形
性质
矩形
1.边:矩形的对边平行且相等
2.角:四个角都是直角:∠ABC=∠BCD=∠ADC=∠BAD=90°.
3.对角线:矩形的对角线② :AC=③ ,
OA=OC,OB=OD.
4.对称性:既是中心对称图形,又是轴对称图形,有④ 条
对称轴.
5.面积:S=ab(a,b分别表示长和宽).
6.拓展:直角三角形斜边上的中线等于斜边的一半.
AB=CD,AD=BC,
AB//CD,AD//① .
BC
互相平分且相等
BD
2
判定
1.定义:有一个角是⑤ 角的平行四边形是矩形. ABCD是矩形
2.对角线相等的⑥ 形是矩形. ABCD是矩形
3.三个角都是⑦ 角的四边形是矩形.
直
ABCD
∠ABC=90°
平行四边
ABCD
AC=BD
直
四边形ABCD
∠DAB=∠ABC=∠BCD=90°
四边形ABCD
是矩形
重点
矩形、菱形和正方形
性质
菱形
1.边:四条边都⑧ ;对边平行:AB∥CD,AD∥BC.
2.角:对角相等,即∠ADC=⑨ ,∠DAB=⑩ .
3. (1)对角线互相垂直且 。
对角线
(2)对角线平分一组 .
4.对称性:既是中心对称图形,又是轴对称图形,有 条对称轴.
5.面积:S= (m,n分别表示两条对角线的长).
相等
∠ABC
∠DCB
平分
AC⊥BD
AO=CO,BO=DO.
对角
AC平分∠DAB与∠BCD,
BD平分∠ABC与∠ADC.
2
判定
1.定义:有一组邻边相等的 是菱形.
2.对角线互相垂直平分的四边形是菱形.
3.四条边都相等的四边形是菱形.
平行四边形
ABCD
AB=BC
ABCD是菱形
四边形ABCD
AC⊥BD
AO=CO,BO=DO
四边形ABCD是菱形
四边形ABCD
AB=BC=CD=AD
四边形ABCD是菱形
重点
矩形、菱形和正方形
正方形
性质
1.边:四条边都相等;对边平行:AB∥CD,AD∥BC.
2.角:四个角都是直角:∠ABC=∠ADC=∠BCD=∠BAD=90°.
3.对角线
(1)对角线互相 。
垂直平分且相等
AC⊥BD,
AO=CO,BO=DO,
AC=BD.
(2)每条对角线 一组对角
平分
∠DAC=∠CAB= ,
∠DCA=∠ACB=45°,
∠ADB=∠BDC= ,
∠ABD=∠DBC=45°.
45°
45°
(3)对称性:既是中心对称图形,又是轴对称图形,有 条对称轴.
(4)面积:S= (a表示正方形边长)= 。
(用对角线计算).
4
a2
重点
矩形、菱形和正方形
正方形
判定
1.有一个角是直角的 形是正方形.
2.有一组邻边相等的 形是正方形.
3.定义:有一组邻边相等,并且有一个角是直角的 形是
正方形.
4.对角线互相 且 的四边形是正方形.
菱
菱形ABCD
∠ABC=90°
菱形ABCD是正方形
矩
矩形ABCD
AB=BC
矩形ABCD是正方形
平行四边
ABCD
AB=BC
∠ABC=90°
ABCD是正方形
垂直平分
相等
四边形ABCD
AC⊥BD
AO=CO,BO=DO
AC=BD
四边形ABCD是正方形
重点
矩形、菱形和正方形
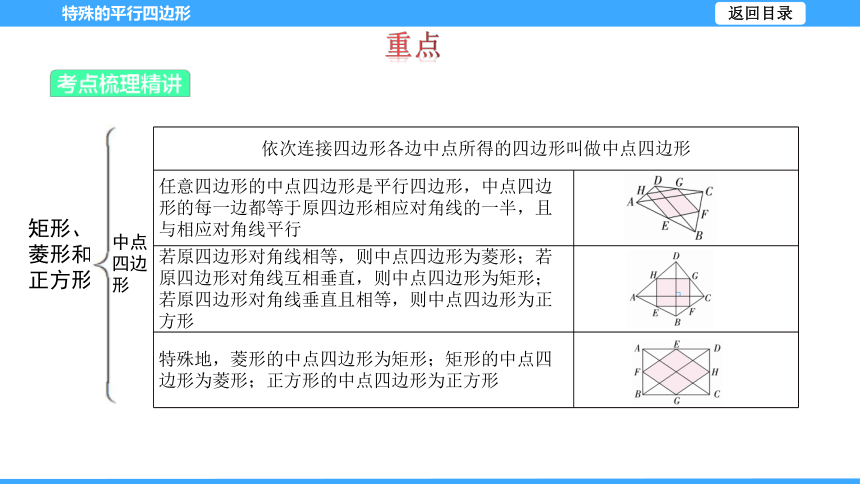
中点四边形
依次连接四边形各边中点所得的四边形叫做中点四边形 任意四边形的中点四边形是平行四边形,中点四边形的每一边都等于原四边形相应对角线的一半,且与相应对角线平行
若原四边形对角线相等,则中点四边形为菱形;若原四边形对角线互相垂直,则中点四边形为矩形;若原四边形对角线垂直且相等,则中点四边形为正方形
特殊地,菱形的中点四边形为矩形;矩形的中点四边形为菱形;正方形的中点四边形为正方形
重点
一、矩形的性质与判定
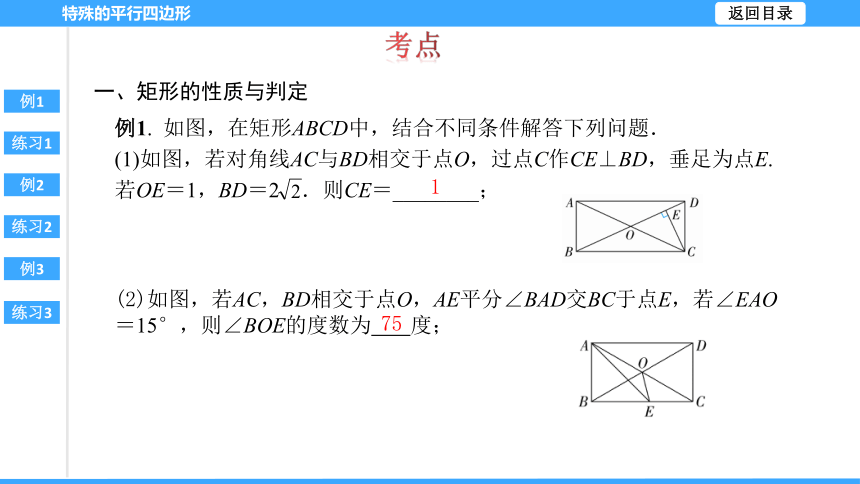
例1. 如图,在矩形ABCD中,结合不同条件解答下列问题.
(1)如图,若对角线AC与BD相交于点O,过点C作CE⊥BD,垂足为点E.若OE=1,BD=2 .则CE=________;
(2)如图,若AC,BD相交于点O,AE平分∠BAD交BC于点E,若∠EAO=15°,则∠BOE的度数为 度;
1
75
考点
(3)如图,如果对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=4,AF=6,则AC的长为 .
解析:如图,连接FC,AE,设AC,EF交于点O.∵EF为AC的垂直平分线,∴AF=FC,AE=EC,AO=OC.∵四边形ABCD是矩形,∴AD∥BC,∠B=90°,
∴∠FAC=∠ECA.在△AFO和△CEO中,
∴△AFO≌△CEO(ASA),∴AF=CE,∴AF=CE=FC=AE=6,∴BC=BE+EC=4+6=10.在Rt△ABE中,AB2=AE2-BE2=20.在Rt△ABC中,
AC=
考点
练习1.如图,已知平行四边形ABCD中,M,N是BD上两点,且BM=DN,AC=2OM.
(1)求证:四边形AMCN是矩形;
(2)若∠BAD=135°,CD=2,AB⊥AC,求对角线MN的长.
解:(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵对角线BD上的两点M,N满足BM=DN,
∴OB-BM=OD-DN,即OM=ON,
∴四边形AMCN是平行四边形.
∵AC=2OM,∴MN=AC,
∴四边形AMCN是矩形.
(2)由(1)得MN=AC.
∵四边形ABCD是平行四边形,
∴AB=CD=2,AD∥BC,
∴∠ABC+∠BAD=180°,
∴∠ABC=45°.
∵AB⊥AC,∴∠BAC=90°,
∴△ABC是等腰直角三角形,
∴AC=AB=2,
∴MN=2.
考点
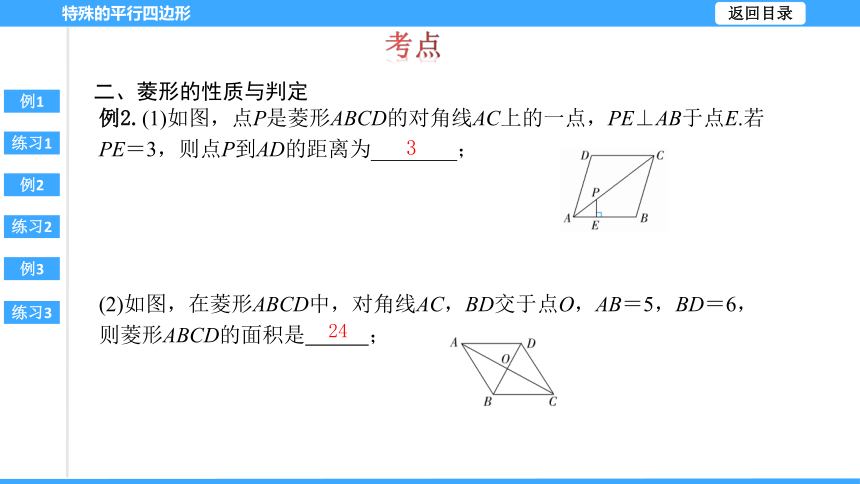
二、菱形的性质与判定
例2.(1)如图,点P是菱形ABCD的对角线AC上的一点,PE⊥AB于点E.若PE=3,则点P到AD的距离为________;
(2)如图,在菱形ABCD中,对角线AC,BD交于点O,AB=5,BD=6,则菱形ABCD的面积是 ;
3
24
考点
例2.(3)如图,已知菱形ABCD的边长为6,点M是对角线AC上的一动点,且∠ABC=120°,则MA+MB+MD的最小值是 .
思路分析:在对角线AC上找一点,使得MA+MB+MD的
最小,根据实际问题分析,一是转化为垂线段最短问题,二是转化为两点间线段最短问题.根据轴对称知MD=MB,而菱形ABCD是形状、大小确定的,通过∠ABC=120°把MA作等线段转化解决.
解析:如图,过点D作DE⊥AB于点E,
交AC于点M,连接BD,MB.∵菱形ABCD中,∠ABC=120°,∴∠DAB=60°,AD=AB=DC=BC,∴△ADB是等边三角形,∴∠MAE=30°,∴AM=2ME.∵MD=MB,∴MA+MB+MD=2ME+2DM=2DE.根据垂线段最短知,此时DE最短,即MA+MB+MD最小.∵菱形ABCD的边长为6,∴DE ∴2DE= .∴MA+MB+MD的最小值是 .
考点
练习2.如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,AC=BD,∠A=∠D.完成下面的填空,并证明你的结论.
(1)若B,C分别是AC,BD的中点,∠A=∠D=30°,当∠AEC
=________°时,四边形BFCE是菱形;
思路分析:
考点
解:当∠AEC=90°时,四边形BFCE是菱形.
∵AE=DF,∠A=∠D,AC=DB,
∴△AEC≌△DFB(SAS),∴EC=FB,∠DFB=∠AEC=90°.
∵B,C分别是AC,BD的中点,
∴EB= AC,FC= BD.
∵∠A=∠D=30°,∴EC= AC,FB= BD.
又∵AC=BD,∴EB=FC=EC=FB,
∴四边形BFCE是菱形.
故答案为:90.
考点
练习2.(2)若∠EBC=60°,AD=12,DC=3.当BE=______时,四边形BFCE是菱形.
思路分析:
解:当BE=6时,四边形BFCE是菱形.
∵AC=BD,∴AC-BC=BD-BC,即AB=DC.
又∵AE=DF,∠A=∠D,∴△ABE≌△DCF(SAS).
∴BE=CF,∠ABE=∠DCF.
∴∠EBC=∠FCB,∴BE∥CF.
∴四边形BFCE是平行四边形.
∵AD=12,DC=3,AB=DC,∴BC=6.
∵∠EBC=60°,BE=BC,
∴△EBC是等边三角形,∴BE=EC=6.
∴平行四边形BFCE是菱形.
故答案为:6.
考点
三、正方形的性质与判定
例3. 如图,在正方形ABCD中,E,F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ.
(1)由旋转的特征可得AQ= ,∠BAQ=∠ ,由正方形的性质可得∠BAD= °,进而可证明△AEQ ≌ ,证明依据: ;
(2)求证:EF2=DF2+BE2;
思路分析:从平方关系看应该运用勾股定理.根据旋转的性质可证∠ABQ=45°,进而证明∠EBQ=90°,在Rt△BEQ中利用等量代换可得EF2=DF2+BE2.
考点
(3)当F是BD的中点时,则四边形AFEQ的形状是 .
思路分析:先证明四边形AFEQ是矩形,再由AQ=AF证得矩形AFEQ是正方形.
解:(1)AF,DAF,90,△AEF,SAS.
(2)证明:∵AB=AD,∠BAD=90°,
∴∠ABE=∠ADF=45°.
由旋转,得∠ABQ=∠ADF=45°,BQ=DF,
∴∠EBQ=∠ABE+∠ABQ=90°,
∴EQ2=BQ2+BE2.
由(1),得△AEQ≌△AEF,∴EQ=EF,
∴EF2=DF2+BE2.
考点
(3)如图,当点F是BD的中点时,则BF=DF,
∴AF⊥BD,∠BAF=∠DAF= ∠BAD=45°.
∵∠EAF=45°,∴∠EAF=∠BAF,
∴AE与AB重合,点E与点B重合,
∴∠AEF=∠ABD=45°,∠AFE=∠AFB=90°.
由旋转,得∠AEQ=∠ADF=45°,∠Q=∠AFD=90°,
∴∠FEQ=90°,
∴四边形AFEQ是矩形.
∵AQ=AF,
∴四边形AFEQ是正方形.
故答案为:正方形.
考点
练习3. 如图,已知四边形ABCD是正方形,分别过A,C两点作l1∥l2,作BM⊥l1于点M,DN⊥l1于点N,直线MB,ND分别交l2于Q,P.求证:四边形PQMN是正方形.
证明:∵l1∥l2,BM⊥l1,DN⊥l2,
∴∠QMN=∠QPN=∠PNM=90°,
∴四边形PQMN为矩形.
∵∠DAB=∠QMN=∠PNM=90°,
∴∠ADN+∠NAD=90°,∠NAD+∠BAM=90°,
∴∠ADN=∠BAM.
又∵AD=BA,
∴△ABM≌△DAN(AAS),∴AM=DN.
同理AN=DP,
∴AM+AN=DN+DP,即MN=PN.
∴四边形PQMN是正方形.
考点
命题点1 矩形的性质
1.(2020·菏泽中考)如图,矩形ABCD中,AB=5,AD=12,点P在对角线BD上,且BP=BA,连接AP并延长,交DC的延长线于点Q,连接BQ,则BQ的长为________.
解析:∵矩形ABCD中,AB=5,AD=12,∠BAD=∠BCD=90°,∴BD= =13,BC=AD=12,CD=AB=5.∵BP=BA=5,∴PD=BD-BP=8,∴∠BAP=∠BPA=∠DPQ.∵AB∥CD,∴∠BAP=∠DQP,∴∠DPQ=∠DQP,∴DQ=DP=8,∴CQ=DQ-CD=8-5=3.在Rt△BCQ中,根据勾股定理,得BQ= = =
命题点
2.★(2021·白银中考)如图,在矩形ABCD中,E是BC边上一点,∠AED=90°,∠EAD=30°,F是AD边的中点,EF=4cm,则BE=________cm.
6
解析:∵∠AED=90°,F是AD边的中点,EF=4cm,∴AD=2EF=8cm.∵∠EAD=30°,∴AE=AD·cos30°=8× (cm).又∵四边形ABCD是矩形,∴AD∥BC,∠B=90°,∴∠BEA=∠EAD=30°.在Rt△ABE中,BE=AE·cos∠BEA=4 ×cos30°=4 × =6(cm).
命题点
3.(2021·鸡西中考)如图,在△ABC中,D,E,F分别是AB,BC和AC边的中点,请添加一个条件 ,使四边形BEFD为矩形.(填一个即可)
解析:∵D,E,F分别是AB,BC和AC边的中点,∴DF,EF都是△ABC的中位线,∴DF∥BC,EF∥AB,∴四边形BEFD为平行四边形,当∠B=90°时,平行四边形BEFD为矩形.
命题点2 矩形的判定
矩形的判定模型
AB⊥BC
命题点
4.(2020·聊城中考)如图,在?ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,若AD=AF,求证:四边形ABFC是矩形.
证明:∵四边形ABCD是平行四边形,∴AB∥CD,
∴∠BAE=∠CFE,∠ABE=∠FCE.
∵E为BC的中点,∴EB=EC,
∴△ABE≌△FCE(AAS),
∴AB=FC.
∵AB∥CF,
∴四边形ABFC是平行四边形.
∵AD=BC,AD=AF,
∴BC=AF,
∴四边形ABFC是矩形.
命题点
5.(2021·烟台中考)如图,在直角坐标系中,菱形ABCD的顶点A,B,C在坐标轴上,若点B的坐标为(-1,0),∠BCD=120°,则点D的坐标为( )
A.(2,2) B. C. D.
D
命题点3 菱形的性质
解析:∵四边形ABCD是菱形,∠BCD=120°,∴∠ABC=60°.∵B(-1,0),∴OB=1,OA= ,AB=2,∴A(0, ),∴AD=AB=2,∴D(2, ).
命题点
6.(2021·济南中考)已知:如图,在菱形ABCD中,E,F分别是边AD和CD上的点,且∠ABE=∠CBF.求证:DE=DF.
证明:∵四边形ABCD是菱形,
∴AD=CD,AB=CB,∠A=∠C.
∵∠ABE=∠CBF,∴△ABE≌△CBF(ASA),
∴AE=CF,
∴AD-AE=CD-CF,∴DE=DF.
命题点
7.(2021·德州中考)下列选项中能使?ABCD成为菱形的是( )
A.AB=CD B.AB=BC C.∠BAD=90° D.AC=BD
命题点4 菱形的判定
菱形的判定模型
解析:一组邻边相等的平行四边形是菱形.∵AB=BC,∴ ABCD为菱形.
B
命题点
8.(2020·滨州中考)如图,过?ABCD对角线AC与BD的交点E作两条互相垂直的直线,分别交边AB,BC,CD,DA于点P,M,Q,N.
(1)求证:△PBE≌△QDE;
(2)顺次连接点P,M,Q,N,求证:四边形PMQN是菱形.
证明:(1)∵四边形ABCD是平行四边形,
∴EB=ED,AB∥CD,
∴∠EBP=∠EDQ.
在△PBE和△QDE中,
∴△PBE≌△QDE(ASA).
(2)如图,顺次连接P,M,Q,N.
∵△PBE≌△QDE,
∴EP=EQ.
同理,△BME≌△DNE(ASA),
∴EM=EN,
∴四边形PMQN是平行四边形.
又∵PQ⊥MN,
∴四边形PMQN是菱形
命题点
9.(2020·枣庄中考)如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是__________.
命题点5 正方形的性质
解析:如图,连接BD交AC于点O,∵四边形ABCD为正方形,∴BD⊥AC,OD=OB=OA=OC.∵AE=CF=2,∴OA-AE=OC-CF,即OE=OF,∴四边形BEDF为平行四边形.又∵BD⊥EF,∴四边形BEDF为菱形,∴DE=DF=BE=BF.∵AC=BD=8,∴OE
=OF= =2.由勾股定理,得DE= ,∴四边形BEDF的周长=4DE=4× .
命题点
10.(2021·威海中考)如图,在正方形ABCD中,AB=2,E为边AB上一点,F为边BC上一点.连接DE和AF交于点G,连接BG.若AE=BF,则BG的最小值为______________.
解析:如图,取AD的中点T,连接BT,GT.
∵四边形ABCD是正方形,∴AD=AB=2,∠DAE=∠ABF=90°.在△DAE和△ABF中, ∴△DAE≌△ABF(SAS),∴∠ADE=∠BAF.∵∠BAF
+∠DAF=90°,∴∠ADE+∠DAF=90°,∴∠AGD=90°.∵DT=AT,∴GT=AD=1.∵BT= = ,∴BG≥BT-GT,∴BG≥ -1,BG的最小值为 -1.
命题点
命题点6 正方形的判定
正方形的判定模型
命题点
11.★(2021·德州模拟)如图,在矩形ABCD中,AD=6,CD=8,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连接CF.
(1)当DG=2时,求证:四边形EFGH是正方形;
(2)当△FCG的面积为2时,求CG的长.
解:(1)证明:在矩形ABCD中,有∠A=∠D=90°,
∴∠DGH+∠DHG=90°.
在菱形EFGH中,EH=HG.
∵AH=2,DG=2,∴AH=DG,
∴Rt△AEH≌Rt△DHG(HL),
∴∠AHE=∠DGH,
∴∠AHE+∠DHG=90°.
∴∠EHG=90°.
∴四边形EFGH是正方形.
(2)如图,过点F作FM⊥DC于点M,则∠FMG=90°.
∴∠A=∠FMG.
连接EG.由矩形和菱形性质可知,AB∥DC,HE∥GF,
∴∠AEG=∠MGE,∠HEG=∠FGE,
∴∠AEH=∠MGF.
又∵EH=GF,
∴△AEH≌△MGF(AAS),∴FM=AH=2.
∵S△FCG= CG·FM= CG×2=2,
∴CG=2.
命题点
12.(2020·青岛中考)如图,在正方形ABCD中,对角线AC与BD交于点O,点E在CD的延长线上,连接AE,点F是AE的中点,连接OF交AD于点G.若DE=2,OF=3,则点A到DF的距离为____________.
解析:在正方形ABCD中,对角线AC与BD交于点O,∴AO=DO,∠ADC=90°,∴∠ADE=90°.∵点F是AE的中点,∴DF=AF=EF= AE,∴OF垂直平分AD,∴AG=DG,∴FG= DE=1.∵OF=3,∴OG=2.∵AO=CO,∴CD=2OG=4,∴AD=CD=4,∴DG=2,∴DF= 如图,过点A作AH⊥DF于点H,∴∠H=∠ADE=90°,∴S△ADF= DF·AH= AD·FG,∴AH= 即点A到DF的距离为
命题点
1.重点
2.考点
3.命题点
1.理解矩形的概念.
2.探索并证明矩形的性质定理及判定定理.
3.理解菱形的概念.
4.探索并证明菱形的性质定理及判定定理.
5.理解正方形的概念,以及平行四边形、矩形、菱形、正方形之间的关系.
6.探索并证明正方形的性质定理及判定定理.
重点
矩形、菱形和正方形
性质
矩形
1.边:矩形的对边平行且相等
2.角:四个角都是直角:∠ABC=∠BCD=∠ADC=∠BAD=90°.
3.对角线:矩形的对角线② :AC=③ ,
OA=OC,OB=OD.
4.对称性:既是中心对称图形,又是轴对称图形,有④ 条
对称轴.
5.面积:S=ab(a,b分别表示长和宽).
6.拓展:直角三角形斜边上的中线等于斜边的一半.
AB=CD,AD=BC,
AB//CD,AD//① .
BC
互相平分且相等
BD
2
判定
1.定义:有一个角是⑤ 角的平行四边形是矩形. ABCD是矩形
2.对角线相等的⑥ 形是矩形. ABCD是矩形
3.三个角都是⑦ 角的四边形是矩形.
直
ABCD
∠ABC=90°
平行四边
ABCD
AC=BD
直
四边形ABCD
∠DAB=∠ABC=∠BCD=90°
四边形ABCD
是矩形
重点
矩形、菱形和正方形
性质
菱形
1.边:四条边都⑧ ;对边平行:AB∥CD,AD∥BC.
2.角:对角相等,即∠ADC=⑨ ,∠DAB=⑩ .
3. (1)对角线互相垂直且 。
对角线
(2)对角线平分一组 .
4.对称性:既是中心对称图形,又是轴对称图形,有 条对称轴.
5.面积:S= (m,n分别表示两条对角线的长).
相等
∠ABC
∠DCB
平分
AC⊥BD
AO=CO,BO=DO.
对角
AC平分∠DAB与∠BCD,
BD平分∠ABC与∠ADC.
2
判定
1.定义:有一组邻边相等的 是菱形.
2.对角线互相垂直平分的四边形是菱形.
3.四条边都相等的四边形是菱形.
平行四边形
ABCD
AB=BC
ABCD是菱形
四边形ABCD
AC⊥BD
AO=CO,BO=DO
四边形ABCD是菱形
四边形ABCD
AB=BC=CD=AD
四边形ABCD是菱形
重点
矩形、菱形和正方形
正方形
性质
1.边:四条边都相等;对边平行:AB∥CD,AD∥BC.
2.角:四个角都是直角:∠ABC=∠ADC=∠BCD=∠BAD=90°.
3.对角线
(1)对角线互相 。
垂直平分且相等
AC⊥BD,
AO=CO,BO=DO,
AC=BD.
(2)每条对角线 一组对角
平分
∠DAC=∠CAB= ,
∠DCA=∠ACB=45°,
∠ADB=∠BDC= ,
∠ABD=∠DBC=45°.
45°
45°
(3)对称性:既是中心对称图形,又是轴对称图形,有 条对称轴.
(4)面积:S= (a表示正方形边长)= 。
(用对角线计算).
4
a2
重点
矩形、菱形和正方形
正方形
判定
1.有一个角是直角的 形是正方形.
2.有一组邻边相等的 形是正方形.
3.定义:有一组邻边相等,并且有一个角是直角的 形是
正方形.
4.对角线互相 且 的四边形是正方形.
菱
菱形ABCD
∠ABC=90°
菱形ABCD是正方形
矩
矩形ABCD
AB=BC
矩形ABCD是正方形
平行四边
ABCD
AB=BC
∠ABC=90°
ABCD是正方形
垂直平分
相等
四边形ABCD
AC⊥BD
AO=CO,BO=DO
AC=BD
四边形ABCD是正方形
重点
矩形、菱形和正方形
中点四边形
依次连接四边形各边中点所得的四边形叫做中点四边形 任意四边形的中点四边形是平行四边形,中点四边形的每一边都等于原四边形相应对角线的一半,且与相应对角线平行
若原四边形对角线相等,则中点四边形为菱形;若原四边形对角线互相垂直,则中点四边形为矩形;若原四边形对角线垂直且相等,则中点四边形为正方形
特殊地,菱形的中点四边形为矩形;矩形的中点四边形为菱形;正方形的中点四边形为正方形
重点
一、矩形的性质与判定
例1. 如图,在矩形ABCD中,结合不同条件解答下列问题.
(1)如图,若对角线AC与BD相交于点O,过点C作CE⊥BD,垂足为点E.若OE=1,BD=2 .则CE=________;
(2)如图,若AC,BD相交于点O,AE平分∠BAD交BC于点E,若∠EAO=15°,则∠BOE的度数为 度;
1
75
考点
(3)如图,如果对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=4,AF=6,则AC的长为 .
解析:如图,连接FC,AE,设AC,EF交于点O.∵EF为AC的垂直平分线,∴AF=FC,AE=EC,AO=OC.∵四边形ABCD是矩形,∴AD∥BC,∠B=90°,
∴∠FAC=∠ECA.在△AFO和△CEO中,
∴△AFO≌△CEO(ASA),∴AF=CE,∴AF=CE=FC=AE=6,∴BC=BE+EC=4+6=10.在Rt△ABE中,AB2=AE2-BE2=20.在Rt△ABC中,
AC=
考点
练习1.如图,已知平行四边形ABCD中,M,N是BD上两点,且BM=DN,AC=2OM.
(1)求证:四边形AMCN是矩形;
(2)若∠BAD=135°,CD=2,AB⊥AC,求对角线MN的长.
解:(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵对角线BD上的两点M,N满足BM=DN,
∴OB-BM=OD-DN,即OM=ON,
∴四边形AMCN是平行四边形.
∵AC=2OM,∴MN=AC,
∴四边形AMCN是矩形.
(2)由(1)得MN=AC.
∵四边形ABCD是平行四边形,
∴AB=CD=2,AD∥BC,
∴∠ABC+∠BAD=180°,
∴∠ABC=45°.
∵AB⊥AC,∴∠BAC=90°,
∴△ABC是等腰直角三角形,
∴AC=AB=2,
∴MN=2.
考点
二、菱形的性质与判定
例2.(1)如图,点P是菱形ABCD的对角线AC上的一点,PE⊥AB于点E.若PE=3,则点P到AD的距离为________;
(2)如图,在菱形ABCD中,对角线AC,BD交于点O,AB=5,BD=6,则菱形ABCD的面积是 ;
3
24
考点
例2.(3)如图,已知菱形ABCD的边长为6,点M是对角线AC上的一动点,且∠ABC=120°,则MA+MB+MD的最小值是 .
思路分析:在对角线AC上找一点,使得MA+MB+MD的
最小,根据实际问题分析,一是转化为垂线段最短问题,二是转化为两点间线段最短问题.根据轴对称知MD=MB,而菱形ABCD是形状、大小确定的,通过∠ABC=120°把MA作等线段转化解决.
解析:如图,过点D作DE⊥AB于点E,
交AC于点M,连接BD,MB.∵菱形ABCD中,∠ABC=120°,∴∠DAB=60°,AD=AB=DC=BC,∴△ADB是等边三角形,∴∠MAE=30°,∴AM=2ME.∵MD=MB,∴MA+MB+MD=2ME+2DM=2DE.根据垂线段最短知,此时DE最短,即MA+MB+MD最小.∵菱形ABCD的边长为6,∴DE ∴2DE= .∴MA+MB+MD的最小值是 .
考点
练习2.如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,AC=BD,∠A=∠D.完成下面的填空,并证明你的结论.
(1)若B,C分别是AC,BD的中点,∠A=∠D=30°,当∠AEC
=________°时,四边形BFCE是菱形;
思路分析:
考点
解:当∠AEC=90°时,四边形BFCE是菱形.
∵AE=DF,∠A=∠D,AC=DB,
∴△AEC≌△DFB(SAS),∴EC=FB,∠DFB=∠AEC=90°.
∵B,C分别是AC,BD的中点,
∴EB= AC,FC= BD.
∵∠A=∠D=30°,∴EC= AC,FB= BD.
又∵AC=BD,∴EB=FC=EC=FB,
∴四边形BFCE是菱形.
故答案为:90.
考点
练习2.(2)若∠EBC=60°,AD=12,DC=3.当BE=______时,四边形BFCE是菱形.
思路分析:
解:当BE=6时,四边形BFCE是菱形.
∵AC=BD,∴AC-BC=BD-BC,即AB=DC.
又∵AE=DF,∠A=∠D,∴△ABE≌△DCF(SAS).
∴BE=CF,∠ABE=∠DCF.
∴∠EBC=∠FCB,∴BE∥CF.
∴四边形BFCE是平行四边形.
∵AD=12,DC=3,AB=DC,∴BC=6.
∵∠EBC=60°,BE=BC,
∴△EBC是等边三角形,∴BE=EC=6.
∴平行四边形BFCE是菱形.
故答案为:6.
考点
三、正方形的性质与判定
例3. 如图,在正方形ABCD中,E,F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ.
(1)由旋转的特征可得AQ= ,∠BAQ=∠ ,由正方形的性质可得∠BAD= °,进而可证明△AEQ ≌ ,证明依据: ;
(2)求证:EF2=DF2+BE2;
思路分析:从平方关系看应该运用勾股定理.根据旋转的性质可证∠ABQ=45°,进而证明∠EBQ=90°,在Rt△BEQ中利用等量代换可得EF2=DF2+BE2.
考点
(3)当F是BD的中点时,则四边形AFEQ的形状是 .
思路分析:先证明四边形AFEQ是矩形,再由AQ=AF证得矩形AFEQ是正方形.
解:(1)AF,DAF,90,△AEF,SAS.
(2)证明:∵AB=AD,∠BAD=90°,
∴∠ABE=∠ADF=45°.
由旋转,得∠ABQ=∠ADF=45°,BQ=DF,
∴∠EBQ=∠ABE+∠ABQ=90°,
∴EQ2=BQ2+BE2.
由(1),得△AEQ≌△AEF,∴EQ=EF,
∴EF2=DF2+BE2.
考点
(3)如图,当点F是BD的中点时,则BF=DF,
∴AF⊥BD,∠BAF=∠DAF= ∠BAD=45°.
∵∠EAF=45°,∴∠EAF=∠BAF,
∴AE与AB重合,点E与点B重合,
∴∠AEF=∠ABD=45°,∠AFE=∠AFB=90°.
由旋转,得∠AEQ=∠ADF=45°,∠Q=∠AFD=90°,
∴∠FEQ=90°,
∴四边形AFEQ是矩形.
∵AQ=AF,
∴四边形AFEQ是正方形.
故答案为:正方形.
考点
练习3. 如图,已知四边形ABCD是正方形,分别过A,C两点作l1∥l2,作BM⊥l1于点M,DN⊥l1于点N,直线MB,ND分别交l2于Q,P.求证:四边形PQMN是正方形.
证明:∵l1∥l2,BM⊥l1,DN⊥l2,
∴∠QMN=∠QPN=∠PNM=90°,
∴四边形PQMN为矩形.
∵∠DAB=∠QMN=∠PNM=90°,
∴∠ADN+∠NAD=90°,∠NAD+∠BAM=90°,
∴∠ADN=∠BAM.
又∵AD=BA,
∴△ABM≌△DAN(AAS),∴AM=DN.
同理AN=DP,
∴AM+AN=DN+DP,即MN=PN.
∴四边形PQMN是正方形.
考点
命题点1 矩形的性质
1.(2020·菏泽中考)如图,矩形ABCD中,AB=5,AD=12,点P在对角线BD上,且BP=BA,连接AP并延长,交DC的延长线于点Q,连接BQ,则BQ的长为________.
解析:∵矩形ABCD中,AB=5,AD=12,∠BAD=∠BCD=90°,∴BD= =13,BC=AD=12,CD=AB=5.∵BP=BA=5,∴PD=BD-BP=8,∴∠BAP=∠BPA=∠DPQ.∵AB∥CD,∴∠BAP=∠DQP,∴∠DPQ=∠DQP,∴DQ=DP=8,∴CQ=DQ-CD=8-5=3.在Rt△BCQ中,根据勾股定理,得BQ= = =
命题点
2.★(2021·白银中考)如图,在矩形ABCD中,E是BC边上一点,∠AED=90°,∠EAD=30°,F是AD边的中点,EF=4cm,则BE=________cm.
6
解析:∵∠AED=90°,F是AD边的中点,EF=4cm,∴AD=2EF=8cm.∵∠EAD=30°,∴AE=AD·cos30°=8× (cm).又∵四边形ABCD是矩形,∴AD∥BC,∠B=90°,∴∠BEA=∠EAD=30°.在Rt△ABE中,BE=AE·cos∠BEA=4 ×cos30°=4 × =6(cm).
命题点
3.(2021·鸡西中考)如图,在△ABC中,D,E,F分别是AB,BC和AC边的中点,请添加一个条件 ,使四边形BEFD为矩形.(填一个即可)
解析:∵D,E,F分别是AB,BC和AC边的中点,∴DF,EF都是△ABC的中位线,∴DF∥BC,EF∥AB,∴四边形BEFD为平行四边形,当∠B=90°时,平行四边形BEFD为矩形.
命题点2 矩形的判定
矩形的判定模型
AB⊥BC
命题点
4.(2020·聊城中考)如图,在?ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,若AD=AF,求证:四边形ABFC是矩形.
证明:∵四边形ABCD是平行四边形,∴AB∥CD,
∴∠BAE=∠CFE,∠ABE=∠FCE.
∵E为BC的中点,∴EB=EC,
∴△ABE≌△FCE(AAS),
∴AB=FC.
∵AB∥CF,
∴四边形ABFC是平行四边形.
∵AD=BC,AD=AF,
∴BC=AF,
∴四边形ABFC是矩形.
命题点
5.(2021·烟台中考)如图,在直角坐标系中,菱形ABCD的顶点A,B,C在坐标轴上,若点B的坐标为(-1,0),∠BCD=120°,则点D的坐标为( )
A.(2,2) B. C. D.
D
命题点3 菱形的性质
解析:∵四边形ABCD是菱形,∠BCD=120°,∴∠ABC=60°.∵B(-1,0),∴OB=1,OA= ,AB=2,∴A(0, ),∴AD=AB=2,∴D(2, ).
命题点
6.(2021·济南中考)已知:如图,在菱形ABCD中,E,F分别是边AD和CD上的点,且∠ABE=∠CBF.求证:DE=DF.
证明:∵四边形ABCD是菱形,
∴AD=CD,AB=CB,∠A=∠C.
∵∠ABE=∠CBF,∴△ABE≌△CBF(ASA),
∴AE=CF,
∴AD-AE=CD-CF,∴DE=DF.
命题点
7.(2021·德州中考)下列选项中能使?ABCD成为菱形的是( )
A.AB=CD B.AB=BC C.∠BAD=90° D.AC=BD
命题点4 菱形的判定
菱形的判定模型
解析:一组邻边相等的平行四边形是菱形.∵AB=BC,∴ ABCD为菱形.
B
命题点
8.(2020·滨州中考)如图,过?ABCD对角线AC与BD的交点E作两条互相垂直的直线,分别交边AB,BC,CD,DA于点P,M,Q,N.
(1)求证:△PBE≌△QDE;
(2)顺次连接点P,M,Q,N,求证:四边形PMQN是菱形.
证明:(1)∵四边形ABCD是平行四边形,
∴EB=ED,AB∥CD,
∴∠EBP=∠EDQ.
在△PBE和△QDE中,
∴△PBE≌△QDE(ASA).
(2)如图,顺次连接P,M,Q,N.
∵△PBE≌△QDE,
∴EP=EQ.
同理,△BME≌△DNE(ASA),
∴EM=EN,
∴四边形PMQN是平行四边形.
又∵PQ⊥MN,
∴四边形PMQN是菱形
命题点
9.(2020·枣庄中考)如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是__________.
命题点5 正方形的性质
解析:如图,连接BD交AC于点O,∵四边形ABCD为正方形,∴BD⊥AC,OD=OB=OA=OC.∵AE=CF=2,∴OA-AE=OC-CF,即OE=OF,∴四边形BEDF为平行四边形.又∵BD⊥EF,∴四边形BEDF为菱形,∴DE=DF=BE=BF.∵AC=BD=8,∴OE
=OF= =2.由勾股定理,得DE= ,∴四边形BEDF的周长=4DE=4× .
命题点
10.(2021·威海中考)如图,在正方形ABCD中,AB=2,E为边AB上一点,F为边BC上一点.连接DE和AF交于点G,连接BG.若AE=BF,则BG的最小值为______________.
解析:如图,取AD的中点T,连接BT,GT.
∵四边形ABCD是正方形,∴AD=AB=2,∠DAE=∠ABF=90°.在△DAE和△ABF中, ∴△DAE≌△ABF(SAS),∴∠ADE=∠BAF.∵∠BAF
+∠DAF=90°,∴∠ADE+∠DAF=90°,∴∠AGD=90°.∵DT=AT,∴GT=AD=1.∵BT= = ,∴BG≥BT-GT,∴BG≥ -1,BG的最小值为 -1.
命题点
命题点6 正方形的判定
正方形的判定模型
命题点
11.★(2021·德州模拟)如图,在矩形ABCD中,AD=6,CD=8,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连接CF.
(1)当DG=2时,求证:四边形EFGH是正方形;
(2)当△FCG的面积为2时,求CG的长.
解:(1)证明:在矩形ABCD中,有∠A=∠D=90°,
∴∠DGH+∠DHG=90°.
在菱形EFGH中,EH=HG.
∵AH=2,DG=2,∴AH=DG,
∴Rt△AEH≌Rt△DHG(HL),
∴∠AHE=∠DGH,
∴∠AHE+∠DHG=90°.
∴∠EHG=90°.
∴四边形EFGH是正方形.
(2)如图,过点F作FM⊥DC于点M,则∠FMG=90°.
∴∠A=∠FMG.
连接EG.由矩形和菱形性质可知,AB∥DC,HE∥GF,
∴∠AEG=∠MGE,∠HEG=∠FGE,
∴∠AEH=∠MGF.
又∵EH=GF,
∴△AEH≌△MGF(AAS),∴FM=AH=2.
∵S△FCG= CG·FM= CG×2=2,
∴CG=2.
命题点
12.(2020·青岛中考)如图,在正方形ABCD中,对角线AC与BD交于点O,点E在CD的延长线上,连接AE,点F是AE的中点,连接OF交AD于点G.若DE=2,OF=3,则点A到DF的距离为____________.
解析:在正方形ABCD中,对角线AC与BD交于点O,∴AO=DO,∠ADC=90°,∴∠ADE=90°.∵点F是AE的中点,∴DF=AF=EF= AE,∴OF垂直平分AD,∴AG=DG,∴FG= DE=1.∵OF=3,∴OG=2.∵AO=CO,∴CD=2OG=4,∴AD=CD=4,∴DG=2,∴DF= 如图,过点A作AH⊥DF于点H,∴∠H=∠ADE=90°,∴S△ADF= DF·AH= AD·FG,∴AH= 即点A到DF的距离为
命题点
