【大单元教学】鲁教版2023年八年级大单元 第七章 二次根式 课件(15张PPT)
文档属性
| 名称 | 【大单元教学】鲁教版2023年八年级大单元 第七章 二次根式 课件(15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 277.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 11:25:52 | ||
图片预览






文档简介
(共15张PPT)
二次根式
课标要求:
了解二次根式、最简二次根式的的概念,了解二次根式(根号下仅限于数)加、减、乘、除运算法则,会用它们进行简单的四则运算。
单元内容:
本单元的主要内容是二次根式的概念,二次根式的加减,二次根式的乘除,最简二次根式。
单元目标:
1、知道二次根式的概念;
2、能进行二次根式的加减运算;
3、能进行二次根式的乘除运算;
4、能把一个二次根式化成最简二次根式,并会合并同类二次根式。
单元学情:
对学生已知内容的掌握程度可通过检测反馈进行了解,对学生的学习方法、学习习惯、兴趣等的了解要在平时的学习中进行充分的观察了解。对新知内容如何设计尝试自学,对未知内容一遇到学习障碍如何能突破,同时在学习中本单元有何特点、习惯怎样、兴趣如何要及时提前做好充分的了解。
作业设计:
本单元作业尽可能做到面向全体学生,进行分层分类设计,做到单元教学设计整体评价和单元课程资源合理利用。
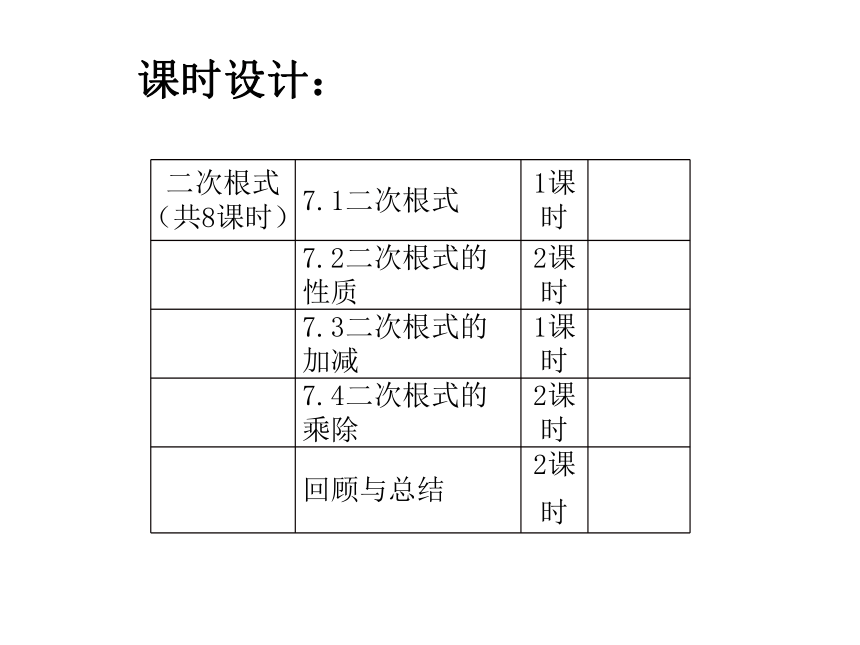
课时设计:
二次根式(共8课时) 7.1二次根式 1课时
7.2二次根式的性质 2课时
7.3二次根式的加减 1课时
7.4二次根式的乘除 2课时
回顾与总结 2课时
二次根式的有关概念
1.二次根式:一般地,形如(①≥0)的式子叫做二次根式.
2.二次根式有意义的条件:被开方数②≥0.
3.最简二次根式:必须同时满足:(1)被开方数不含③分母;(2)被开方数中不含能开得尽方的因数或因式.
4.同类二次根式:化为最简二次根式后,被开方数④相同的几个二次根式称为同类二次根式.
基础小练
1. (1)使有意义的x的取值范围为x≥9;
(2)在中,自变量x的取值范围是x≤1且x≠-2;
(3)若y=++2,则x+y=5.
2.下列二次根式中,是最简二次根式的是(C)
A. B. C. D.
3.若与是同类二次根式,则符合条件的a的值可以是(C)
A.12 B.14 C. D.24
二次根式的性质:
非负数:
二次根式的运算:
基础小练
二次根式
课标要求:
了解二次根式、最简二次根式的的概念,了解二次根式(根号下仅限于数)加、减、乘、除运算法则,会用它们进行简单的四则运算。
单元内容:
本单元的主要内容是二次根式的概念,二次根式的加减,二次根式的乘除,最简二次根式。
单元目标:
1、知道二次根式的概念;
2、能进行二次根式的加减运算;
3、能进行二次根式的乘除运算;
4、能把一个二次根式化成最简二次根式,并会合并同类二次根式。
单元学情:
对学生已知内容的掌握程度可通过检测反馈进行了解,对学生的学习方法、学习习惯、兴趣等的了解要在平时的学习中进行充分的观察了解。对新知内容如何设计尝试自学,对未知内容一遇到学习障碍如何能突破,同时在学习中本单元有何特点、习惯怎样、兴趣如何要及时提前做好充分的了解。
作业设计:
本单元作业尽可能做到面向全体学生,进行分层分类设计,做到单元教学设计整体评价和单元课程资源合理利用。
课时设计:
二次根式(共8课时) 7.1二次根式 1课时
7.2二次根式的性质 2课时
7.3二次根式的加减 1课时
7.4二次根式的乘除 2课时
回顾与总结 2课时
二次根式的有关概念
1.二次根式:一般地,形如(①≥0)的式子叫做二次根式.
2.二次根式有意义的条件:被开方数②≥0.
3.最简二次根式:必须同时满足:(1)被开方数不含③分母;(2)被开方数中不含能开得尽方的因数或因式.
4.同类二次根式:化为最简二次根式后,被开方数④相同的几个二次根式称为同类二次根式.
基础小练
1. (1)使有意义的x的取值范围为x≥9;
(2)在中,自变量x的取值范围是x≤1且x≠-2;
(3)若y=++2,则x+y=5.
2.下列二次根式中,是最简二次根式的是(C)
A. B. C. D.
3.若与是同类二次根式,则符合条件的a的值可以是(C)
A.12 B.14 C. D.24
二次根式的性质:
非负数:
二次根式的运算:
基础小练
