【大单元教学】鲁教版2023年八年级大单元 二次根式一元二次方程 课件(47张PPT)
文档属性
| 名称 | 【大单元教学】鲁教版2023年八年级大单元 二次根式一元二次方程 课件(47张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 00:00:00 | ||
图片预览







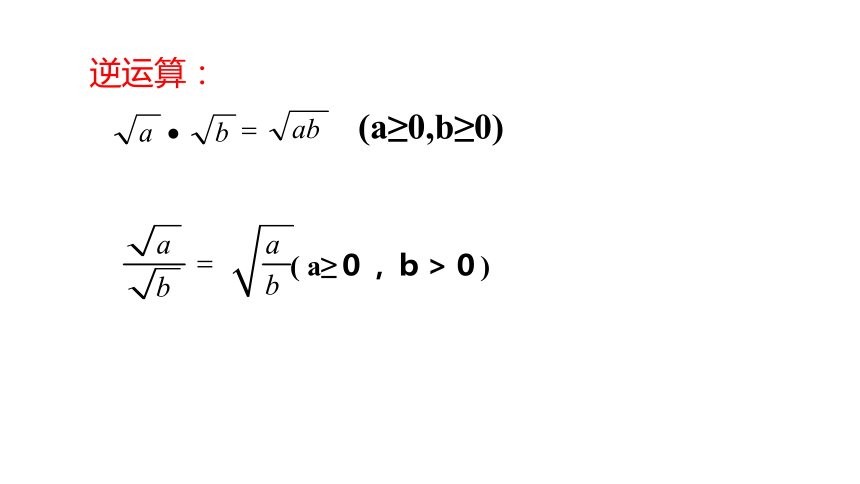



文档简介
(共47张PPT)
二次根式与
学习目标
1.加深理解二次根式的有关概念,熟练掌握二次根式有意义的条件,灵活熟练地化简二次根式,进行二次根式的加减、乘除混合运算。
2.理解一元二次方程的概念,熟练一元二次方程的解法,会用列一元二次方程的方法解决实际问题。
思维导图
②a都是非负数.
1. 形如 (a≥0)的式子叫做二次根式.
a
①都是形如 的式子,
a
其中a为整式或分式,a叫做被开方式.
特点:
);
0
(
0
a
a
≥
≥
的算术平方根
表示
2.因为
)
0
(
,所以
a
a
a
≥
);
0
(
)
(
2
≥
=
a
a
a
1.下列各式: 中,一定是二次根式的个数有 ( )
A.3个 B.4个 C.5个 D.6个
2. 当a是怎样的实数时,下列各式在实数范围内有意义?
解:由a-1≥0,得 a≥1
解:由2a+3≥0,得
解:(1) =2.1;
(2) =22× =4×3=12.
计算:(1) ;(2) .
1.二次根式的性质
);
0
(
0
a
a
≥
≥
2.积的算术平方根的性质:
3.商的算术平方根的性质:
(a≥0,b≥0)
逆运算:
( a≥0,b>0)
化简: (1)
(2)
(4)
1、被开方数中不含分母;
2、被开方数中不含能开尽方的因数或因式。
像这样的二次根式叫做最简二次根式
判断下列各式中哪些是最简二次根式?
(1)
(3)
(4)
(2)
同类二次根式
一般地,二次根式相加减,先把各个二次根式分别化成最简二次根式,然后再将同类二次根式分别合并.有括号时,要先去括号.
几个二次根式化简成最简二次根式后,如果它们的被开方数相同,那么这几个二次根式是同类二次根式.
计算:
.
解:
=
(3)合并同类二次根式。
一化
二找
三合并
二次根式加减法的步骤:
(1)将每个二次根式化为最简二次根式;
(2)找出其中的同类二次根式;
),
0
,
0
(
≥
≥
b
a
·
b
a
=
ab
).
0
,
0
(
>
≥
b
a
b
a
=
b
a
1.
二次根式的乘法和除法法则:
2.二次根式相乘除,先按照法则进行运算,如果积 或商中含有二次根式,要将它化成最简二次根式.
二次根式的乘除
计算:
;
6
24
)
2
(
;
14
7
)
1
(
·
练习:
二次根式的混合运算
例题展示:
练习:
提示:a -ab+b =(a+b) -3ab=(a-b) +ab
关键:a -ab+b 与(a+b) 或(a-b) 的关系
一元二次方程及一般形式:
1.只含有_____个未知数,且未知数的最高次数为______的________方程叫做一元二次方程.
2.一元二次方程的一般形式是________________(a≠0);其中a是二次项系数,b是一次项系数 ,c是 常数项.
一
2
整式
ax2+bx+c=0
1、判断下面哪些方程是一元二次方程:
√
√
×
×
×
×
( )
×
2、把方程(1-x)(2-x)=3-x2 化为一般形式是:___________, 其二次项系数是____,一次项系数是____,常数项是____.
3、方程(m-2)x|m| +3mx-4=0是关于x的一元二次方程,则 ( )
A.m=±2 B.m=2 C.m=-2 D.m≠ ±2
4、若x=2是方程x2+ax-8=0的根,则a=______.
一元二次方程的解法
因式分解法
开平方法
配方法
公式法
你能说出每一种解法的特点吗
方程的左边是完全平方式,右边是非负数;即形如x2=a(a≥0)
1.化1:把二次项系数化为1;
2.移项:把常数项移到方程的右边;
3.配方:方程两边同加一次项系数一半的平方;
4.变形:化成
5.开平方,求解
“配方法”解方程的基本步骤
★一除、二移、三配、四化、五解.
用公式法解一元二次方程的前提是:
1.必需是一般形式的一元二次方程:
ax2+bx+c=0(a≠0).
2.b2-4ac≥0.
1.用因式分解法的条件是:方程左边能够分解,而右边等于零;
2.理论依据是:如果两个因式的积等于零那么至少有一个因式等于零.
因式分解法解一元二次方程的一般步骤:
一移-----方程的右边=0;
二分-----方程的左边因式分解;
三化-----方程化为两个一元一次方程;
四解-----写出方程两个解;
① x2-3x+1=0 ② 3x2-1=0
③ -3t2+t=0 ④ x2-4x=2
⑤ 2x2-x=0 ⑥ 5(m+2)2=8
⑦ 3y2-y-1=0 ⑧ 2x2+4x-1=0
⑨ (x-2)2=2(x-2)
适合运用直接开平方法 ;
适合运用因式分解法 ;
适合运用公式法 ;
适合运用配方法 .
选一选
例:解一元二次方程
1.用直接开平方法:(x+2)2=9
3.用公式法解方程 :3x2=4x+7
2.用因式分解法解方(y+2)2=3(y+2)
4.用配方法解方程 :4x2-8x-5=0
用适当的方法求解下列方程:
1) (x+1)(x-3)=1
2) 2(x-3)=3x(x-3)
3) (x+1)(x-3)=2x-5
4) (x+1)2-2(x-1)2=7
一元二次方程根的判别式
两不相等实根
两相等实根
无实根
一元二次方程
根的情况
定理与逆定理
两个不相等实根
两个相等实根
无实根(无解)
若一元二次方程有实数根,则
例题:求证:关于x的方程
x2-(m+2)x+2m-1=0有两个不相等的实数根.
1、关于x的一元二次方程
有实数根,则m的取值范围是__ _____.
2、关于x的方程 有实数根,
则整数a的最大值是_______.
练习:
3 、若关于的一元二次方程 有两个不相等的实数根,则的取值范围是( )
B. 且
C. D. 且
若方程ax2+bx+c=0(a≠0)的两根为x1、x2 ,则
x1+x2 = x1·x2=
若方程x2+px+q=0(a≠0)的两根 为x1、x2 ,则
x1+x2 = x1·x2=
一元二次方程根与系数关系(韦达定理)
1、关于x的一元二次方程x +(m-1)x-5=0, 当
m ___时,方程的两根为互为相反数.
2、关于x的一元二次方程3x -5x+ (m-1)=0, 当m ___时,方程的两根为互为倒数.
=1
=4
若方程的两根为互为相反数,则b=0。
若方程的两根为互为倒数,则a=c。
3 、 已知 是关于x的一元二次方程
的两根,是否存在实数k,使 成立?
1. 审清题意,弄清题中的已知量和未知量找出题中的等量关系。
2. 恰当地设出未知数,用未知数的代数式表示未知量。
3. 根据题中的等量关系列出方程。
4. 解方程得出方程的解。
5. 检验看方程的解是否符合题意。
6. 作答注意单位。
列方程解应用题的解题过程
一元二次方程的应用
2、数字问题
3、变化率问题、疾病传播问题
5、面积问题
4、利润问题
1、增长率
注意: ①设要有单位
②解出方程后检验根的合理性
6、几何问题
例1:甲公司前年缴税40万元,今年缴税48.4万元.该公司缴税的年平均增长率为多少
增长率问题
某电冰箱厂每个月的产量都比上个月增长的百分数相同。已知该厂今年4月份的电冰箱产量为5万台,6月份比5月份多生产了12000台,求该厂今年产量的月平均增长率为多少
利润型
某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元
解:设每千克水果应涨价x元,
依题意得: (500-20x)(10+x)=6000
整理得: x2-15x+50=0
解这个方程得:x1=5 x2=10
要使顾客得到实惠应取x=5
答:每千克水果应涨价 5元.
每每型
如图,在一块长92m,宽60m的矩形耕地上挖三条水渠,水渠的宽度都相等.水渠把耕地分成面积均为885m2的6个矩形小块,水渠应挖多宽.
图形面积问题
1、两个数的差等于4,积等于45,求这两个数.
数字问题
一次会议上,每两个参加会议的人都互相握了一次手,有人统计一共握了66次手.这次会议到会的人数是多少
握手问题
通过这节课的学习,反思你的收获。
二次根式与
学习目标
1.加深理解二次根式的有关概念,熟练掌握二次根式有意义的条件,灵活熟练地化简二次根式,进行二次根式的加减、乘除混合运算。
2.理解一元二次方程的概念,熟练一元二次方程的解法,会用列一元二次方程的方法解决实际问题。
思维导图
②a都是非负数.
1. 形如 (a≥0)的式子叫做二次根式.
a
①都是形如 的式子,
a
其中a为整式或分式,a叫做被开方式.
特点:
);
0
(
0
a
a
≥
≥
的算术平方根
表示
2.因为
)
0
(
,所以
a
a
a
≥
);
0
(
)
(
2
≥
=
a
a
a
1.下列各式: 中,一定是二次根式的个数有 ( )
A.3个 B.4个 C.5个 D.6个
2. 当a是怎样的实数时,下列各式在实数范围内有意义?
解:由a-1≥0,得 a≥1
解:由2a+3≥0,得
解:(1) =2.1;
(2) =22× =4×3=12.
计算:(1) ;(2) .
1.二次根式的性质
);
0
(
0
a
a
≥
≥
2.积的算术平方根的性质:
3.商的算术平方根的性质:
(a≥0,b≥0)
逆运算:
( a≥0,b>0)
化简: (1)
(2)
(4)
1、被开方数中不含分母;
2、被开方数中不含能开尽方的因数或因式。
像这样的二次根式叫做最简二次根式
判断下列各式中哪些是最简二次根式?
(1)
(3)
(4)
(2)
同类二次根式
一般地,二次根式相加减,先把各个二次根式分别化成最简二次根式,然后再将同类二次根式分别合并.有括号时,要先去括号.
几个二次根式化简成最简二次根式后,如果它们的被开方数相同,那么这几个二次根式是同类二次根式.
计算:
.
解:
=
(3)合并同类二次根式。
一化
二找
三合并
二次根式加减法的步骤:
(1)将每个二次根式化为最简二次根式;
(2)找出其中的同类二次根式;
),
0
,
0
(
≥
≥
b
a
·
b
a
=
ab
).
0
,
0
(
>
≥
b
a
b
a
=
b
a
1.
二次根式的乘法和除法法则:
2.二次根式相乘除,先按照法则进行运算,如果积 或商中含有二次根式,要将它化成最简二次根式.
二次根式的乘除
计算:
;
6
24
)
2
(
;
14
7
)
1
(
·
练习:
二次根式的混合运算
例题展示:
练习:
提示:a -ab+b =(a+b) -3ab=(a-b) +ab
关键:a -ab+b 与(a+b) 或(a-b) 的关系
一元二次方程及一般形式:
1.只含有_____个未知数,且未知数的最高次数为______的________方程叫做一元二次方程.
2.一元二次方程的一般形式是________________(a≠0);其中a是二次项系数,b是一次项系数 ,c是 常数项.
一
2
整式
ax2+bx+c=0
1、判断下面哪些方程是一元二次方程:
√
√
×
×
×
×
( )
×
2、把方程(1-x)(2-x)=3-x2 化为一般形式是:___________, 其二次项系数是____,一次项系数是____,常数项是____.
3、方程(m-2)x|m| +3mx-4=0是关于x的一元二次方程,则 ( )
A.m=±2 B.m=2 C.m=-2 D.m≠ ±2
4、若x=2是方程x2+ax-8=0的根,则a=______.
一元二次方程的解法
因式分解法
开平方法
配方法
公式法
你能说出每一种解法的特点吗
方程的左边是完全平方式,右边是非负数;即形如x2=a(a≥0)
1.化1:把二次项系数化为1;
2.移项:把常数项移到方程的右边;
3.配方:方程两边同加一次项系数一半的平方;
4.变形:化成
5.开平方,求解
“配方法”解方程的基本步骤
★一除、二移、三配、四化、五解.
用公式法解一元二次方程的前提是:
1.必需是一般形式的一元二次方程:
ax2+bx+c=0(a≠0).
2.b2-4ac≥0.
1.用因式分解法的条件是:方程左边能够分解,而右边等于零;
2.理论依据是:如果两个因式的积等于零那么至少有一个因式等于零.
因式分解法解一元二次方程的一般步骤:
一移-----方程的右边=0;
二分-----方程的左边因式分解;
三化-----方程化为两个一元一次方程;
四解-----写出方程两个解;
① x2-3x+1=0 ② 3x2-1=0
③ -3t2+t=0 ④ x2-4x=2
⑤ 2x2-x=0 ⑥ 5(m+2)2=8
⑦ 3y2-y-1=0 ⑧ 2x2+4x-1=0
⑨ (x-2)2=2(x-2)
适合运用直接开平方法 ;
适合运用因式分解法 ;
适合运用公式法 ;
适合运用配方法 .
选一选
例:解一元二次方程
1.用直接开平方法:(x+2)2=9
3.用公式法解方程 :3x2=4x+7
2.用因式分解法解方(y+2)2=3(y+2)
4.用配方法解方程 :4x2-8x-5=0
用适当的方法求解下列方程:
1) (x+1)(x-3)=1
2) 2(x-3)=3x(x-3)
3) (x+1)(x-3)=2x-5
4) (x+1)2-2(x-1)2=7
一元二次方程根的判别式
两不相等实根
两相等实根
无实根
一元二次方程
根的情况
定理与逆定理
两个不相等实根
两个相等实根
无实根(无解)
若一元二次方程有实数根,则
例题:求证:关于x的方程
x2-(m+2)x+2m-1=0有两个不相等的实数根.
1、关于x的一元二次方程
有实数根,则m的取值范围是__ _____.
2、关于x的方程 有实数根,
则整数a的最大值是_______.
练习:
3 、若关于的一元二次方程 有两个不相等的实数根,则的取值范围是( )
B. 且
C. D. 且
若方程ax2+bx+c=0(a≠0)的两根为x1、x2 ,则
x1+x2 = x1·x2=
若方程x2+px+q=0(a≠0)的两根 为x1、x2 ,则
x1+x2 = x1·x2=
一元二次方程根与系数关系(韦达定理)
1、关于x的一元二次方程x +(m-1)x-5=0, 当
m ___时,方程的两根为互为相反数.
2、关于x的一元二次方程3x -5x+ (m-1)=0, 当m ___时,方程的两根为互为倒数.
=1
=4
若方程的两根为互为相反数,则b=0。
若方程的两根为互为倒数,则a=c。
3 、 已知 是关于x的一元二次方程
的两根,是否存在实数k,使 成立?
1. 审清题意,弄清题中的已知量和未知量找出题中的等量关系。
2. 恰当地设出未知数,用未知数的代数式表示未知量。
3. 根据题中的等量关系列出方程。
4. 解方程得出方程的解。
5. 检验看方程的解是否符合题意。
6. 作答注意单位。
列方程解应用题的解题过程
一元二次方程的应用
2、数字问题
3、变化率问题、疾病传播问题
5、面积问题
4、利润问题
1、增长率
注意: ①设要有单位
②解出方程后检验根的合理性
6、几何问题
例1:甲公司前年缴税40万元,今年缴税48.4万元.该公司缴税的年平均增长率为多少
增长率问题
某电冰箱厂每个月的产量都比上个月增长的百分数相同。已知该厂今年4月份的电冰箱产量为5万台,6月份比5月份多生产了12000台,求该厂今年产量的月平均增长率为多少
利润型
某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元
解:设每千克水果应涨价x元,
依题意得: (500-20x)(10+x)=6000
整理得: x2-15x+50=0
解这个方程得:x1=5 x2=10
要使顾客得到实惠应取x=5
答:每千克水果应涨价 5元.
每每型
如图,在一块长92m,宽60m的矩形耕地上挖三条水渠,水渠的宽度都相等.水渠把耕地分成面积均为885m2的6个矩形小块,水渠应挖多宽.
图形面积问题
1、两个数的差等于4,积等于45,求这两个数.
数字问题
一次会议上,每两个参加会议的人都互相握了一次手,有人统计一共握了66次手.这次会议到会的人数是多少
握手问题
通过这节课的学习,反思你的收获。
