第二十章 数据的分析 章末复习课件(39张PPT)
文档属性
| 名称 | 第二十章 数据的分析 章末复习课件(39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 556.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 00:00:00 | ||
图片预览







文档简介
(共39张PPT)
第二十章数据的分析
(4个概念3个应用2种思想)
八年级下册
单元复习过过过
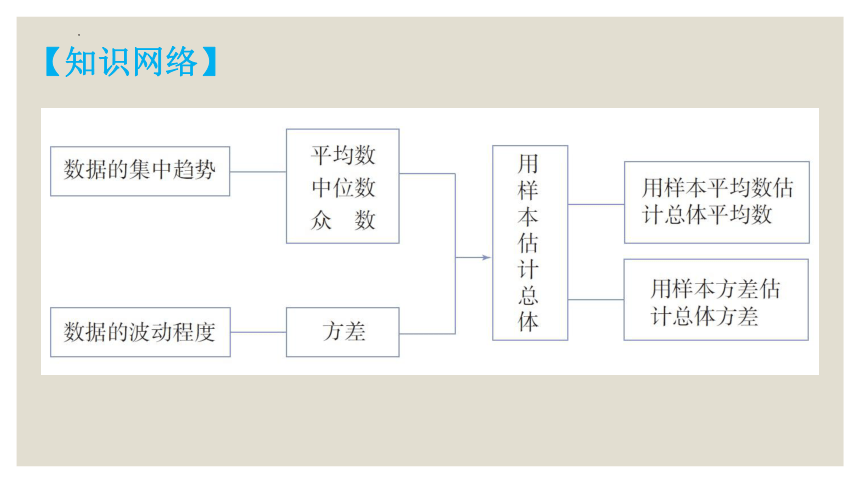
【知识网络】
知识回顾
一
求平均数、中位数、众数和方差的方法
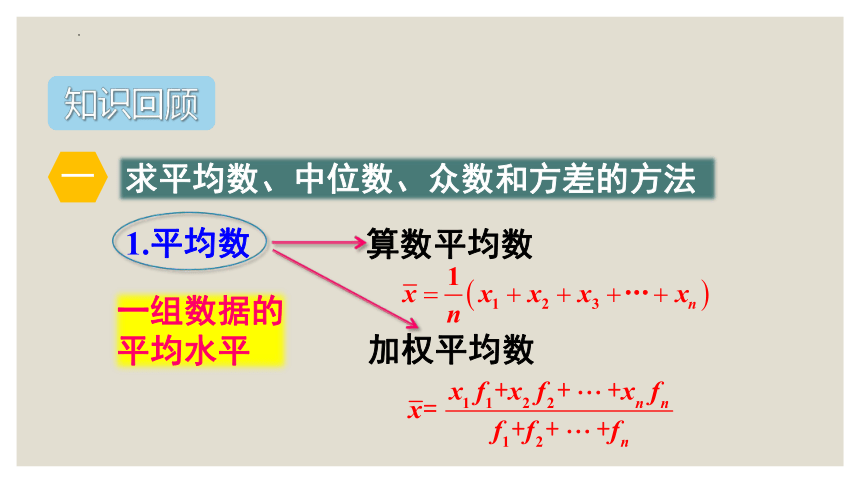
1.平均数
算数平均数
加权平均数
一组数据的平均水平
算术平均数和加权平均数有什么区别和联系?
算术平均数和加权平均数都是求n个数的平均数;不同的是加权平均数有侧重点,反映问题更全面,更深入。
加权平均数中“权”有什么意义?
反映数据的相对“重要程度”。
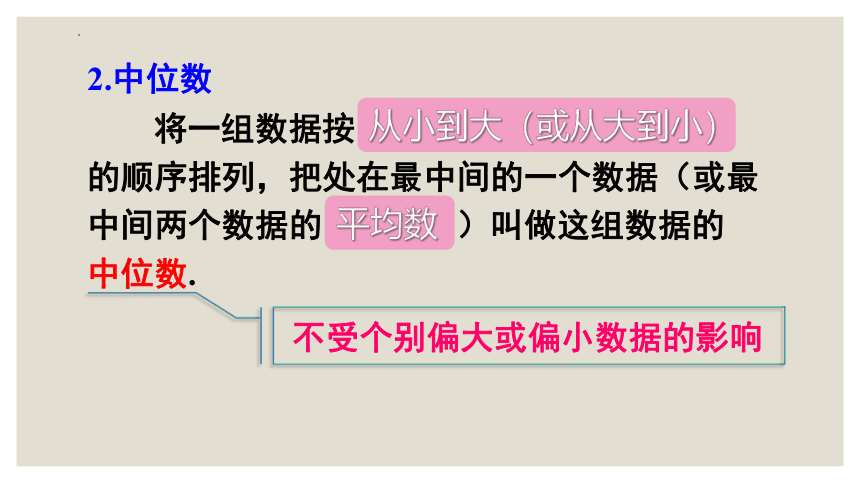
2.中位数
将一组数据按 的顺序排列,把处在最中间的一个数据(或最中间两个数据的 )叫做这组数据的 中位数.
从小到大(或从大到小)
平均数
不受个别偏大或偏小数据的影响
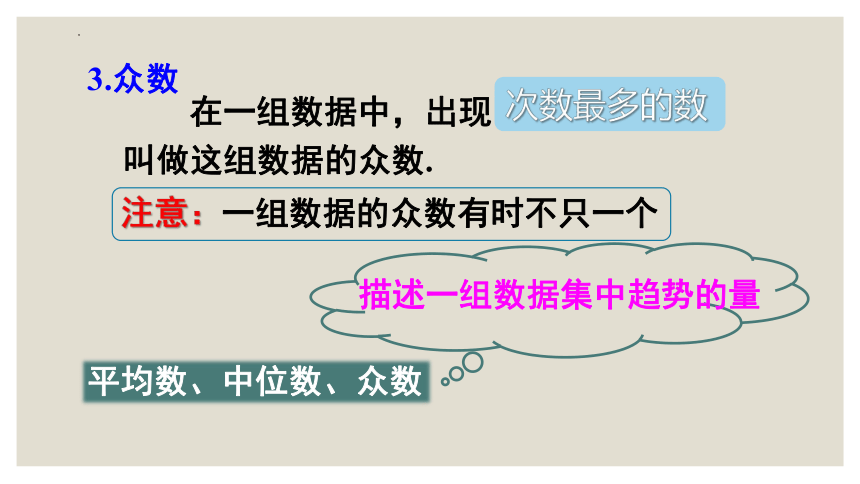
3.众数
在一组数据中,出现 叫做这组数据的众数.
次数最多的数
平均数、中位数、众数
描述一组数据集中趋势的量
注意:一组数据的众数有时不只一个
4.方差
方差是用来反映一组数据的 的特征数,常常用来比较两组数据的 .
波动程度
稳定性
方差
数据的波动
方差
数据的波动
公式:
二
本章数学思想方法
1.方程思想的运用
2.数形结合
从图形中得到必要的信息是解决问题的关键.
4个概念
考点01 平均数
1 [2022·四川内江中考]某4S店今年1~5月新能源汽车的销量(辆数)分别如下:25,33,36,31,40,这组数据的平均数是( B )
A.34 B.33 C.32.5 D.31
解析:这组数据的平均数为(25+33+36+31+40)÷5=33.故选B.
B
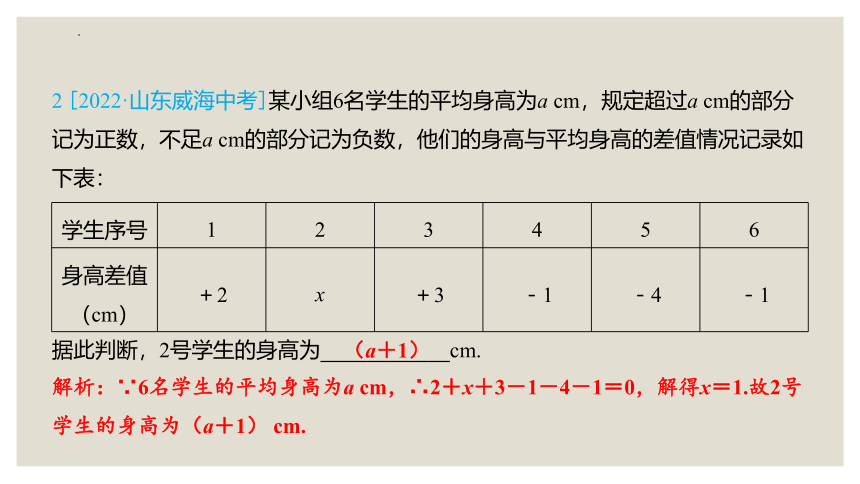
2 [2022·山东威海中考]某小组6名学生的平均身高为a cm,规定超过a cm的部分记为正数,不足a cm的部分记为负数,他们的身高与平均身高的差值情况记录如下表:
学生序号 1 2 3 4 5 6
身高差值 (cm) +2 x +3 -1 -4 -1
据此判断,2号学生的身高为 (a+1) cm.
解析:∵6名学生的平均身高为a cm,∴2+x+3-1-4-1=0,解得x=1.故2号学生的身高为(a+1) cm.
(a+1)
考点02 中位数
3 [2022·湖南株洲中考]某路段的一台机动车雷达测速仪记录了一段时间内通过的机动车的车速数据如下:67,63,69,55,65,则该组数据的中位数为( B )
A.63 B.65 C.66 D.69
解析:将这组数据按由小到大的顺序排列,为55,63,65,67,69,所以这组数据的中位数是65.故选B.
B
考点03 众数
4 [2022·河南中考]如图的扇形统计图描述了某校学生对课后延时服务的打分情况(满分为5分),则所打分数的众数为( B )
A.5分 B.4分
C.3分 D.45%
(第4题图)
解析:由扇形统计图知,打4分的人数占总人数的45%,人数最多,所以所打分数的众数为4分.故选B.
B
考点04 方差
5 [2022·山东滨州中考]今年我国小麦大丰收,农业专家在某种植片区随机抽取了10株小麦,测得其麦穗长(单位:cm)分别为8,8,6,7,9,9,7,8,10,8,那么这一组数据的方差为( D )
A.1.5 B.1.4 C.1.3 D.1.2
解析:这一组数据的平均数为×(8+8+6+7+9+9+7+8+10+8)=8,所以这一组数据的方差为×[4×(8-8)2+(6-8)2+2×(7-8)2+2×(9-8)2+(10-8)2]=1.2.故选D.
D
6 [2022·湖北恩施中考]为了解某小区居民的用水情况,随机抽查了若干户家庭的某月用水量,统计结果如下表:
月用水量/吨 3 4 5 6
户数 4 6 8 2
关于这若干户家庭的该月用水量的数据统计分析,下列说法正确的是( A )
A.众数是5吨 B.平均数是7吨
C.中位数是5吨 D.方差是1
A
解析:这组数据出现次数最多的是5吨,共出现8次,所以月用水量的众数是5吨,因此选项A符合题意;这组数据的平均数为(3×4+4×6+5×8+6×2)÷(4+6+8+2)=4.4(吨),因此选项B不符合题意;将这20户的月用水量按从小到大的顺序排列,处在中间位置的两个数据的平均数为=4.5(吨),因此选项C不符合题意;这组数据的方差为[(3-4.4)2×4+(4-4.4)2×6+(5-4.4)2×8+(6-4.4)2×2]=0.84,因此选项D不符合题意.故选A.
3个应用
考点05 平均数、中位数、众数的应用
7 [2021·山东临沂中考]实施乡村振兴计划以来,我市农村经济发展进入了快车道,为了了解梁家岭村今年一季度经济发展状况,小玉同学的课题研究小组从该村300户家庭中随机抽取了20户,收集到他们一季度家庭人均收入(单位:万元)的数据如下:
0.69 0.73 0.74 0.80 0.81 0.98 0.93
0.81 0.89 0.69 0.74 0.99 0.98 0.78
0.80 0.89 0.83 0.89 0.94 0.89
分组 频数
0.65≤x<0.70 2
0.70≤x<0.75 3
0.75≤x<0.80 1
0.80≤x<0.85 a
0.85≤x<0.90 4
0.90≤x<0.95 2
0.95≤x<1.00 b
研究小组的同学对以上数据进行了整理分析,如下表:
统计量 平均数 中位数 众数
数值 0.84 c d
(1)a= 5 ,b= 3 ,c= 0.82 ,d= 0.89 .
解:(1)由统计频数的方法,得a=5,b=3.
将A村家庭人均收入从小到大排列,处在中间位置的两个数的平均数为(0.81+0.83)÷2=0.82.
因此中位数是0.82,即c=0.82.
他们一季度家庭人均收入的数据出现次数最多的是0.89,
因此众数是0.89,即d=0.89.
5
3
0.82
0.89
(2)试估计今年一季度梁家岭村家庭人均收入不低于0.8万元的户数.
解:(2)300×=210(户),
故估计今年一季度梁家岭村家庭人均收入不低于0.8万元的户数为210.
(3)该村梁飞家今年一季度人均收入为0.83万元,能否超过村里一半以上的家庭?请说明理由.
解:(3)该村梁飞家今年一季度人均收入为0.83万元,能超过村里一半以上的家庭.理由如下:
因为该村一季度家庭人均收入的中位数是0.82,0.83>0.82,
所以该村梁飞家今年一季度人均收入为0.83万元,能超过村里一半以上的家庭.
考点06 方差的应用
8 [2022·江苏扬州中考]某射击运动队进行了五次射击测试,甲、乙两名选手的测试成绩如图,甲、乙两名选手成绩的方差分别记为,,则 > .(填“>”“<”或“=”)
>
(第8题图)
解析:由题图可知,甲的波动性较大,乙的波动性小,即甲的方差大,乙的方差小,∴>.
9 新趋势 跨学科实践 [2022·山西中考]生物学研究表明,植物光合作用速率越高,单位时间内合成的有机物越多.为了解甲、乙两个品种大豆的光合作用速率,科研人员从甲、乙两个品种的大豆中各选五株,在同等实验条件下,测量它们的光合作用速率(单位:μmol·m-2·s-1),结果统计如下:
品种 第一株 第二株 第三株 第四株 第五株 平均数
甲 32 30 25 18 20 25
乙 28 25 26 24 22 25
(第9题图)
则这两个大豆品种光合作用速率更稳定的是 乙 (填“甲”或“乙”).
解析:甲的方差为=[(32-25)2+(30-25)2+(25-25)2+(18-25)2+(20-25)2]=29.6;乙的方差为
=[(28-25)2+(25-25)2+(26-25)2+(24-25)2+(22-25)2]=4.∵29.6>4,∴这两个大豆品种光合作用速率更稳定的是乙.
乙
考点07 用样本估计总体的应用
10 [2022·山东枣庄中考]每年的6月6日为“全国爱眼日”.某初中学校为了解本校学生的视力健康状况,组织数学兴趣小组按下列步骤来开展统计活动.
一、确定调查对象
(1)有以下三种调查方案:
方案一:从七年级抽取140名学生,进行视力状况调查;
方案二:从七年级、八年级中各随机抽取140名学生,进行视力状况调查;
方案三:从全校1 600名学生中随机抽取600名学生,进行视力状况调查.
其中,最具有代表性和广泛性的抽样调查方案是 方案三 .
方案三
二、收集整理数据
按照国家视力健康标准,学生视力状况分为A,B,C,D四个类别.数学兴趣小组随机抽取本校部分学生进行调查,绘制成如下不完整的统计图表.
抽取的学生视力状况统计图
(第10题图)
类别 A B C D
视力 视力≥ 5.0 4.9 4.6≤视力 ≤4.8 视力≤
4.5
健康 状况 视力 正常 轻度视 力不良 中度视 力不良 重度视
力不良
人数 160 m n 56
抽取的学生视力状况统计表
三、分析数据,解答问题
(2)调查视力数据的中位数所在类别为 B 类.
(3)该校共有学生1 600人,请估算该校学生中,中度视力不良和重度视力不良的总人数.
解:(3)调查的总人数为160÷40%=400,
由题意可知,m=400×16%=64,
所以n=400-64-56-160=120,
1 600×=704.
所以估算该校学生中,中度视力不良和重度视力不良的总人数为704.
B
(4)为更好地保护视力,结合上述统计数据分析,请你提出一条合理化的建议.
解:(4)该校学生近视程度为中度及以上的占44%,说明该校学生近视程度较为严重,建议学校加强电子产品进校园及使用的管控(答案不唯一).
2种数学思想的运用
考点08 方程思想的运用
11 [2022·黑龙江齐齐哈尔中考]数据1,2,3,4,5,x存在唯一众数,且该组数据的平均数等于众数,则x的值为( B )
A.2 B.3 C.4 D.5
解析:∵该组数据有唯一众数,且1,2,3,4,5各出现一次,∴众数一定是x.∵这6个数的平均数等于众数,∴1+2+3+4+5=5x,解得x=3.故选B.
B
12 [2022·黑龙江牡丹江中考]一列数据1,2,3,x,5,5的平均数是4,则这组数据的中位数是 4 .
解析:由题意知,=4,解得x=8,∴这组数据为1,2,3,5,5,8,∴这组数据的中位数是=4.
4
考点09 数形结合思想的运用
13 [2022·江苏南通中考]为了了解八年级学生本学期参加社会实践活动的天数情况,从A,B两个县区分别随机抽查了200名八年级学生,根据调查结果绘制了统计图表,部分图表如下:
A,B两个县区的统计表
平均数 众数 中位数
A县区 3.35 3 3
B县区 3.35 4 2.5
(1)若A县区八年级共有约5 000名学生,估计该县区八年级学生参加社会实践活动不少于3天的学生为 3750 名.
3750
(2)请对A,B两个县区八年级学生参加社会实践活动的天数情况进行比较,作出判断,并说明理由.
A县区统计图
(第13题图)
解:(2)因为A,B两个县区的平均数一样,从众数来看B县区参加社会实践活动的天数情况好,但从中位数来看A县区参加社会实践活动的天数情况好.
基础巩固
1. 在共有15人参加的演讲比赛中,参赛选手的成绩各不相同,因此选手要想知道自己是否进入前8名,只需要了解自己的成绩以及全部选手成绩的( )
A.平均数 B.众数 C.中位数 D.方差
C
2. 九(1)班五个劳动竞赛小组一天植树的棵数分别是:10,10,12,x,8,如果这组数据的众数与平均数相等,那么这组数据的中位数是 .
10
综合应用
3.为了全面了解学生的学习、生活及家庭的基本情况,加强学校、家庭的联系,梅灿中学积极组织全体教师开展“课外访万家活动”,王老师对所在班级的全体学生进行实地家访,了解到每名学生家庭的相关信息,现从中随机抽取15名学生家庭的年收入情况,数据如下表:
(1)求这15名学生家庭年收入的平均数、中位数、众数;
(2)你认为用(1)中的哪个数据来代表这15名学生家庭年收入的一般水平较为合适?请简要说明理由.
解:(1)平均数:4.3,中位数3,众数3;
(2)3万元代表这15名学生家庭年收入的一般水平较为合适.
因为3万元既是中位数,又是众数,代表了大部分家庭年收入的一般情况,也是家庭最多的一个收入水平,所以3万元比较合适.
拓展延伸
4.为选派一名学生参加全市实践活动技能竞赛,A,B两位同学在校实习基地现场进行加工直径为20mm的零件的测试,他俩各加工的零件个数、直径等相关数据依次如下图所示(单位:mm).根据测试得到的有关数据,试解答下列问题:
(1)考虑平均数与完全符合要求的个数,你认为 的成绩好些;
(2)计算出s2B的大小,考虑平均数与方差,说明谁的成绩好些;
B
∴B的成绩更稳定
(3)考虑图中折线走势及竞赛中加工零件个数远远超过10个后实际情况,你认为派谁去参赛较合适?说明你的理由.
由(2)可知B的成绩较为稳定,且由图象可看出,B加工的第九个零件后成绩越来越好,而竞赛中加工零件个数远远超过10个,所以应派B去参赛.
第二十章数据的分析
(4个概念3个应用2种思想)
八年级下册
单元复习过过过
【知识网络】
知识回顾
一
求平均数、中位数、众数和方差的方法
1.平均数
算数平均数
加权平均数
一组数据的平均水平
算术平均数和加权平均数有什么区别和联系?
算术平均数和加权平均数都是求n个数的平均数;不同的是加权平均数有侧重点,反映问题更全面,更深入。
加权平均数中“权”有什么意义?
反映数据的相对“重要程度”。
2.中位数
将一组数据按 的顺序排列,把处在最中间的一个数据(或最中间两个数据的 )叫做这组数据的 中位数.
从小到大(或从大到小)
平均数
不受个别偏大或偏小数据的影响
3.众数
在一组数据中,出现 叫做这组数据的众数.
次数最多的数
平均数、中位数、众数
描述一组数据集中趋势的量
注意:一组数据的众数有时不只一个
4.方差
方差是用来反映一组数据的 的特征数,常常用来比较两组数据的 .
波动程度
稳定性
方差
数据的波动
方差
数据的波动
公式:
二
本章数学思想方法
1.方程思想的运用
2.数形结合
从图形中得到必要的信息是解决问题的关键.
4个概念
考点01 平均数
1 [2022·四川内江中考]某4S店今年1~5月新能源汽车的销量(辆数)分别如下:25,33,36,31,40,这组数据的平均数是( B )
A.34 B.33 C.32.5 D.31
解析:这组数据的平均数为(25+33+36+31+40)÷5=33.故选B.
B
2 [2022·山东威海中考]某小组6名学生的平均身高为a cm,规定超过a cm的部分记为正数,不足a cm的部分记为负数,他们的身高与平均身高的差值情况记录如下表:
学生序号 1 2 3 4 5 6
身高差值 (cm) +2 x +3 -1 -4 -1
据此判断,2号学生的身高为 (a+1) cm.
解析:∵6名学生的平均身高为a cm,∴2+x+3-1-4-1=0,解得x=1.故2号学生的身高为(a+1) cm.
(a+1)
考点02 中位数
3 [2022·湖南株洲中考]某路段的一台机动车雷达测速仪记录了一段时间内通过的机动车的车速数据如下:67,63,69,55,65,则该组数据的中位数为( B )
A.63 B.65 C.66 D.69
解析:将这组数据按由小到大的顺序排列,为55,63,65,67,69,所以这组数据的中位数是65.故选B.
B
考点03 众数
4 [2022·河南中考]如图的扇形统计图描述了某校学生对课后延时服务的打分情况(满分为5分),则所打分数的众数为( B )
A.5分 B.4分
C.3分 D.45%
(第4题图)
解析:由扇形统计图知,打4分的人数占总人数的45%,人数最多,所以所打分数的众数为4分.故选B.
B
考点04 方差
5 [2022·山东滨州中考]今年我国小麦大丰收,农业专家在某种植片区随机抽取了10株小麦,测得其麦穗长(单位:cm)分别为8,8,6,7,9,9,7,8,10,8,那么这一组数据的方差为( D )
A.1.5 B.1.4 C.1.3 D.1.2
解析:这一组数据的平均数为×(8+8+6+7+9+9+7+8+10+8)=8,所以这一组数据的方差为×[4×(8-8)2+(6-8)2+2×(7-8)2+2×(9-8)2+(10-8)2]=1.2.故选D.
D
6 [2022·湖北恩施中考]为了解某小区居民的用水情况,随机抽查了若干户家庭的某月用水量,统计结果如下表:
月用水量/吨 3 4 5 6
户数 4 6 8 2
关于这若干户家庭的该月用水量的数据统计分析,下列说法正确的是( A )
A.众数是5吨 B.平均数是7吨
C.中位数是5吨 D.方差是1
A
解析:这组数据出现次数最多的是5吨,共出现8次,所以月用水量的众数是5吨,因此选项A符合题意;这组数据的平均数为(3×4+4×6+5×8+6×2)÷(4+6+8+2)=4.4(吨),因此选项B不符合题意;将这20户的月用水量按从小到大的顺序排列,处在中间位置的两个数据的平均数为=4.5(吨),因此选项C不符合题意;这组数据的方差为[(3-4.4)2×4+(4-4.4)2×6+(5-4.4)2×8+(6-4.4)2×2]=0.84,因此选项D不符合题意.故选A.
3个应用
考点05 平均数、中位数、众数的应用
7 [2021·山东临沂中考]实施乡村振兴计划以来,我市农村经济发展进入了快车道,为了了解梁家岭村今年一季度经济发展状况,小玉同学的课题研究小组从该村300户家庭中随机抽取了20户,收集到他们一季度家庭人均收入(单位:万元)的数据如下:
0.69 0.73 0.74 0.80 0.81 0.98 0.93
0.81 0.89 0.69 0.74 0.99 0.98 0.78
0.80 0.89 0.83 0.89 0.94 0.89
分组 频数
0.65≤x<0.70 2
0.70≤x<0.75 3
0.75≤x<0.80 1
0.80≤x<0.85 a
0.85≤x<0.90 4
0.90≤x<0.95 2
0.95≤x<1.00 b
研究小组的同学对以上数据进行了整理分析,如下表:
统计量 平均数 中位数 众数
数值 0.84 c d
(1)a= 5 ,b= 3 ,c= 0.82 ,d= 0.89 .
解:(1)由统计频数的方法,得a=5,b=3.
将A村家庭人均收入从小到大排列,处在中间位置的两个数的平均数为(0.81+0.83)÷2=0.82.
因此中位数是0.82,即c=0.82.
他们一季度家庭人均收入的数据出现次数最多的是0.89,
因此众数是0.89,即d=0.89.
5
3
0.82
0.89
(2)试估计今年一季度梁家岭村家庭人均收入不低于0.8万元的户数.
解:(2)300×=210(户),
故估计今年一季度梁家岭村家庭人均收入不低于0.8万元的户数为210.
(3)该村梁飞家今年一季度人均收入为0.83万元,能否超过村里一半以上的家庭?请说明理由.
解:(3)该村梁飞家今年一季度人均收入为0.83万元,能超过村里一半以上的家庭.理由如下:
因为该村一季度家庭人均收入的中位数是0.82,0.83>0.82,
所以该村梁飞家今年一季度人均收入为0.83万元,能超过村里一半以上的家庭.
考点06 方差的应用
8 [2022·江苏扬州中考]某射击运动队进行了五次射击测试,甲、乙两名选手的测试成绩如图,甲、乙两名选手成绩的方差分别记为,,则 > .(填“>”“<”或“=”)
>
(第8题图)
解析:由题图可知,甲的波动性较大,乙的波动性小,即甲的方差大,乙的方差小,∴>.
9 新趋势 跨学科实践 [2022·山西中考]生物学研究表明,植物光合作用速率越高,单位时间内合成的有机物越多.为了解甲、乙两个品种大豆的光合作用速率,科研人员从甲、乙两个品种的大豆中各选五株,在同等实验条件下,测量它们的光合作用速率(单位:μmol·m-2·s-1),结果统计如下:
品种 第一株 第二株 第三株 第四株 第五株 平均数
甲 32 30 25 18 20 25
乙 28 25 26 24 22 25
(第9题图)
则这两个大豆品种光合作用速率更稳定的是 乙 (填“甲”或“乙”).
解析:甲的方差为=[(32-25)2+(30-25)2+(25-25)2+(18-25)2+(20-25)2]=29.6;乙的方差为
=[(28-25)2+(25-25)2+(26-25)2+(24-25)2+(22-25)2]=4.∵29.6>4,∴这两个大豆品种光合作用速率更稳定的是乙.
乙
考点07 用样本估计总体的应用
10 [2022·山东枣庄中考]每年的6月6日为“全国爱眼日”.某初中学校为了解本校学生的视力健康状况,组织数学兴趣小组按下列步骤来开展统计活动.
一、确定调查对象
(1)有以下三种调查方案:
方案一:从七年级抽取140名学生,进行视力状况调查;
方案二:从七年级、八年级中各随机抽取140名学生,进行视力状况调查;
方案三:从全校1 600名学生中随机抽取600名学生,进行视力状况调查.
其中,最具有代表性和广泛性的抽样调查方案是 方案三 .
方案三
二、收集整理数据
按照国家视力健康标准,学生视力状况分为A,B,C,D四个类别.数学兴趣小组随机抽取本校部分学生进行调查,绘制成如下不完整的统计图表.
抽取的学生视力状况统计图
(第10题图)
类别 A B C D
视力 视力≥ 5.0 4.9 4.6≤视力 ≤4.8 视力≤
4.5
健康 状况 视力 正常 轻度视 力不良 中度视 力不良 重度视
力不良
人数 160 m n 56
抽取的学生视力状况统计表
三、分析数据,解答问题
(2)调查视力数据的中位数所在类别为 B 类.
(3)该校共有学生1 600人,请估算该校学生中,中度视力不良和重度视力不良的总人数.
解:(3)调查的总人数为160÷40%=400,
由题意可知,m=400×16%=64,
所以n=400-64-56-160=120,
1 600×=704.
所以估算该校学生中,中度视力不良和重度视力不良的总人数为704.
B
(4)为更好地保护视力,结合上述统计数据分析,请你提出一条合理化的建议.
解:(4)该校学生近视程度为中度及以上的占44%,说明该校学生近视程度较为严重,建议学校加强电子产品进校园及使用的管控(答案不唯一).
2种数学思想的运用
考点08 方程思想的运用
11 [2022·黑龙江齐齐哈尔中考]数据1,2,3,4,5,x存在唯一众数,且该组数据的平均数等于众数,则x的值为( B )
A.2 B.3 C.4 D.5
解析:∵该组数据有唯一众数,且1,2,3,4,5各出现一次,∴众数一定是x.∵这6个数的平均数等于众数,∴1+2+3+4+5=5x,解得x=3.故选B.
B
12 [2022·黑龙江牡丹江中考]一列数据1,2,3,x,5,5的平均数是4,则这组数据的中位数是 4 .
解析:由题意知,=4,解得x=8,∴这组数据为1,2,3,5,5,8,∴这组数据的中位数是=4.
4
考点09 数形结合思想的运用
13 [2022·江苏南通中考]为了了解八年级学生本学期参加社会实践活动的天数情况,从A,B两个县区分别随机抽查了200名八年级学生,根据调查结果绘制了统计图表,部分图表如下:
A,B两个县区的统计表
平均数 众数 中位数
A县区 3.35 3 3
B县区 3.35 4 2.5
(1)若A县区八年级共有约5 000名学生,估计该县区八年级学生参加社会实践活动不少于3天的学生为 3750 名.
3750
(2)请对A,B两个县区八年级学生参加社会实践活动的天数情况进行比较,作出判断,并说明理由.
A县区统计图
(第13题图)
解:(2)因为A,B两个县区的平均数一样,从众数来看B县区参加社会实践活动的天数情况好,但从中位数来看A县区参加社会实践活动的天数情况好.
基础巩固
1. 在共有15人参加的演讲比赛中,参赛选手的成绩各不相同,因此选手要想知道自己是否进入前8名,只需要了解自己的成绩以及全部选手成绩的( )
A.平均数 B.众数 C.中位数 D.方差
C
2. 九(1)班五个劳动竞赛小组一天植树的棵数分别是:10,10,12,x,8,如果这组数据的众数与平均数相等,那么这组数据的中位数是 .
10
综合应用
3.为了全面了解学生的学习、生活及家庭的基本情况,加强学校、家庭的联系,梅灿中学积极组织全体教师开展“课外访万家活动”,王老师对所在班级的全体学生进行实地家访,了解到每名学生家庭的相关信息,现从中随机抽取15名学生家庭的年收入情况,数据如下表:
(1)求这15名学生家庭年收入的平均数、中位数、众数;
(2)你认为用(1)中的哪个数据来代表这15名学生家庭年收入的一般水平较为合适?请简要说明理由.
解:(1)平均数:4.3,中位数3,众数3;
(2)3万元代表这15名学生家庭年收入的一般水平较为合适.
因为3万元既是中位数,又是众数,代表了大部分家庭年收入的一般情况,也是家庭最多的一个收入水平,所以3万元比较合适.
拓展延伸
4.为选派一名学生参加全市实践活动技能竞赛,A,B两位同学在校实习基地现场进行加工直径为20mm的零件的测试,他俩各加工的零件个数、直径等相关数据依次如下图所示(单位:mm).根据测试得到的有关数据,试解答下列问题:
(1)考虑平均数与完全符合要求的个数,你认为 的成绩好些;
(2)计算出s2B的大小,考虑平均数与方差,说明谁的成绩好些;
B
∴B的成绩更稳定
(3)考虑图中折线走势及竞赛中加工零件个数远远超过10个后实际情况,你认为派谁去参赛较合适?说明你的理由.
由(2)可知B的成绩较为稳定,且由图象可看出,B加工的第九个零件后成绩越来越好,而竞赛中加工零件个数远远超过10个,所以应派B去参赛.
