平移旋转应用[上学期]
图片预览

文档简介
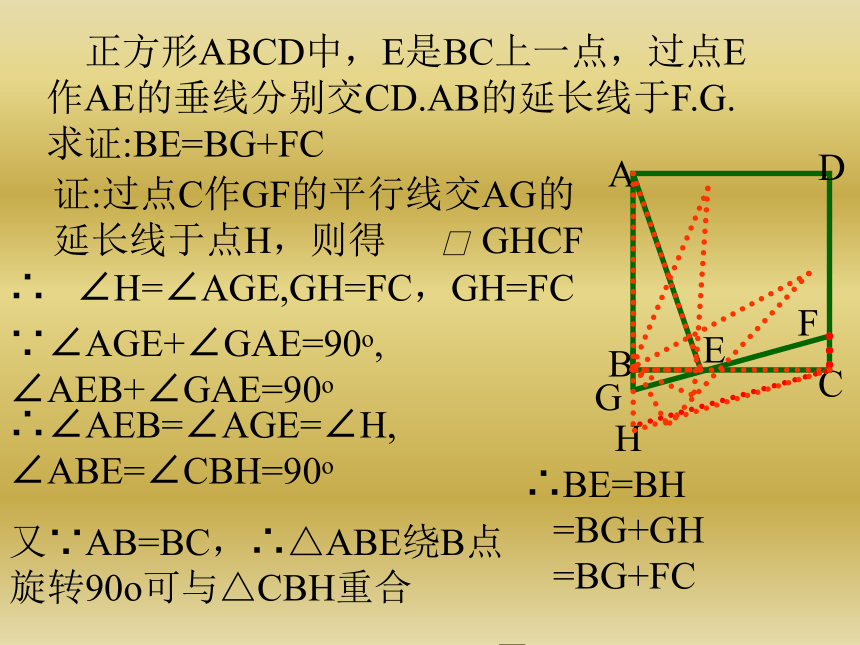
课件62张PPT。 正方形ABCD中,E是BC上一点,过点E作AE的垂线分别交CD.AB的延长线于F.G.求证:BE=BG+FC
∴BE=BH
=BG+GH
=BG+FC∴ ∠H=∠AGE,GH=FC,GH=FC
∵∠AGE+∠GAE=90ο, ∠AEB+∠GAE=90ο∴∠AEB=∠AGE=∠H, ∠ABE=∠CBH=90ο又∵AB=BC,∴△ABE绕B点旋转90ο可与△CBH重合
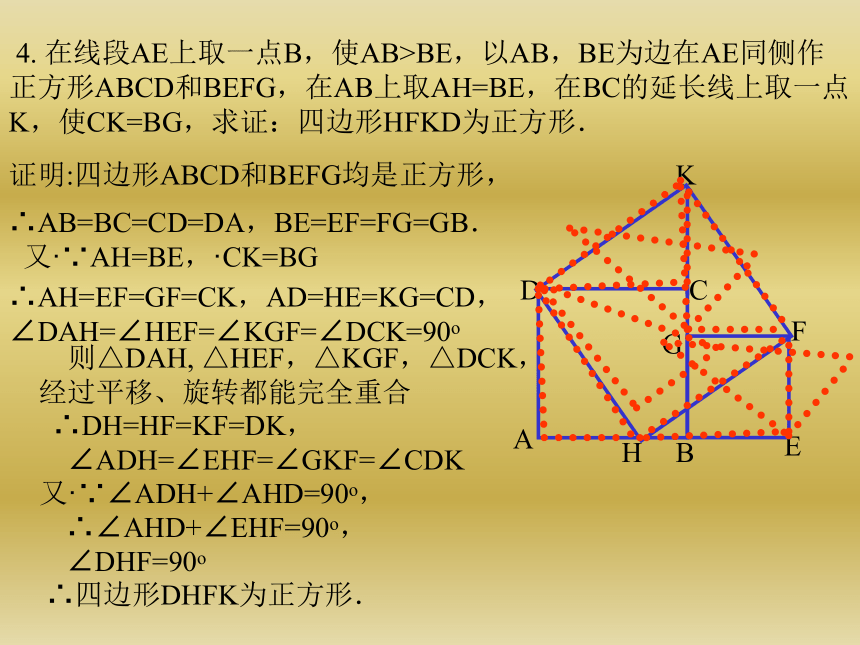
EF 4. 在线段AE上取一点B,使AB>BE,以AB,BE为边在AE同侧作正方形ABCD和BEFG,在AB上取AH=BE,在BC的延长线上取一点K,使CK=BG,求证:四边形HFKD为正方形.∴四边形DHFK为正方形.证明:四边形ABCD和BEFG均是正方形,∴AB=BC=CD=DA,BE=EF=FG=GB.
又·∵AH=BE,·CK=BG∴AH=EF=GF=CK,AD=HE=KG=CD,∠DAH=∠HEF=∠KGF=∠DCK=90ο 则△DAH, △HEF,△KGF,△DCK,经过平移、旋转都能完全重合∴DH=HF=KF=DK,
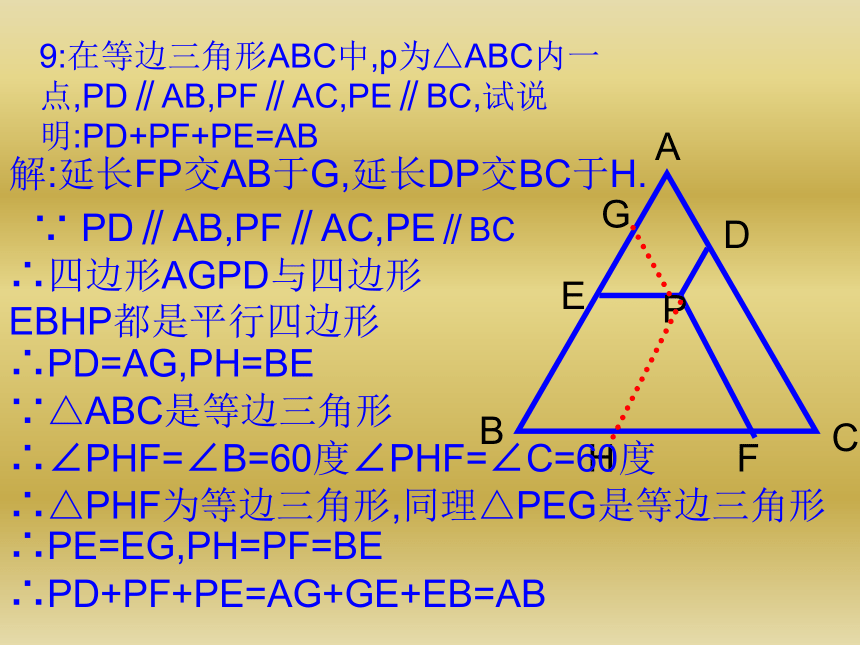
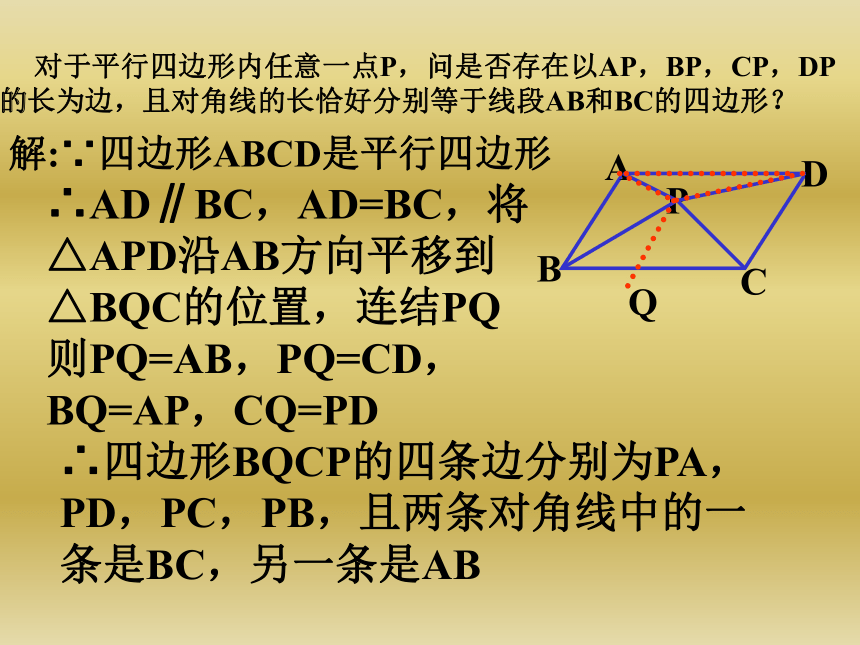
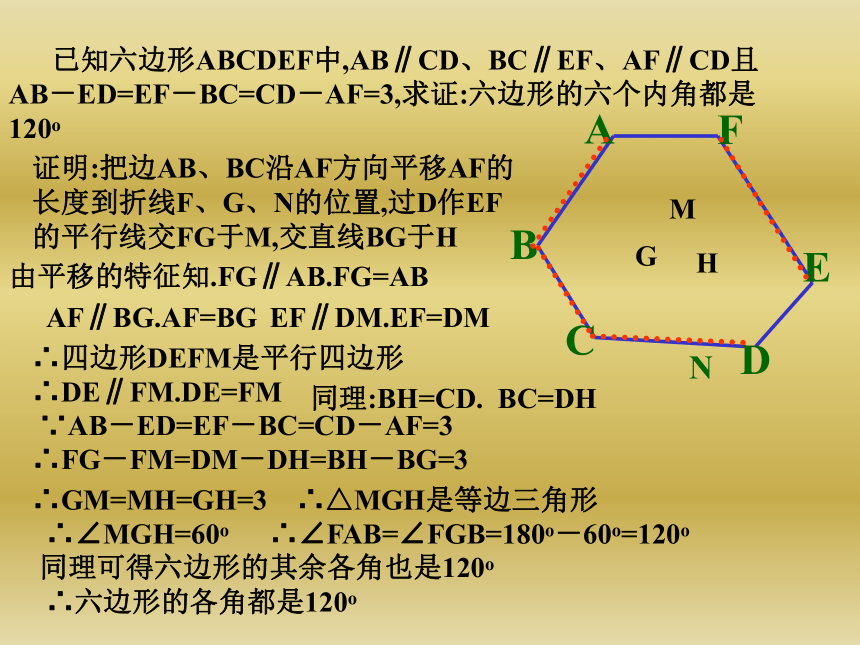
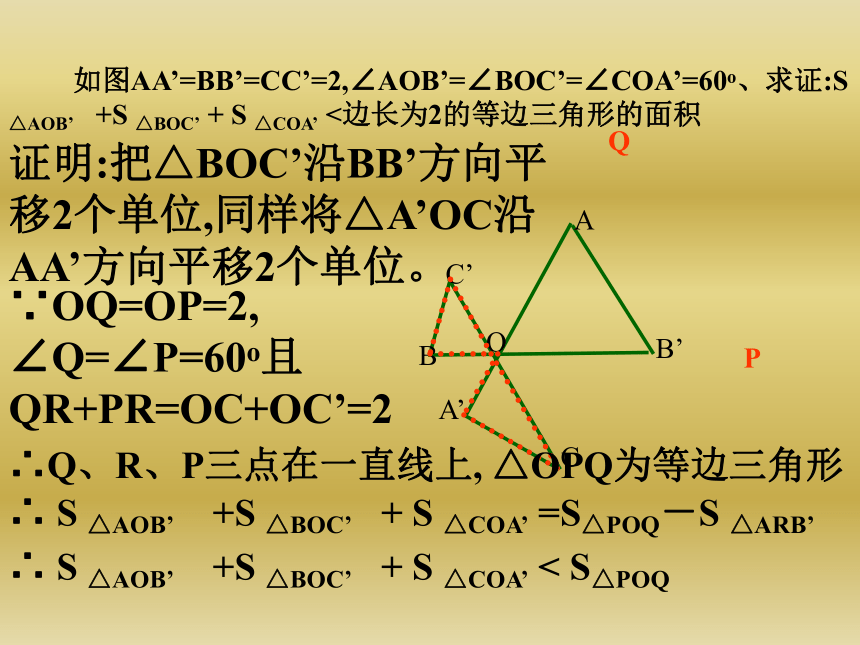
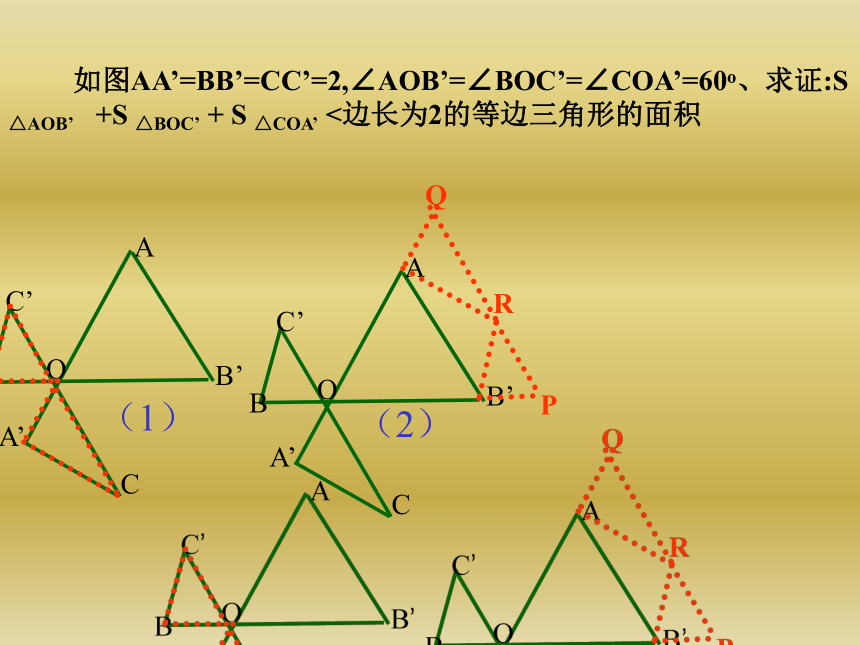
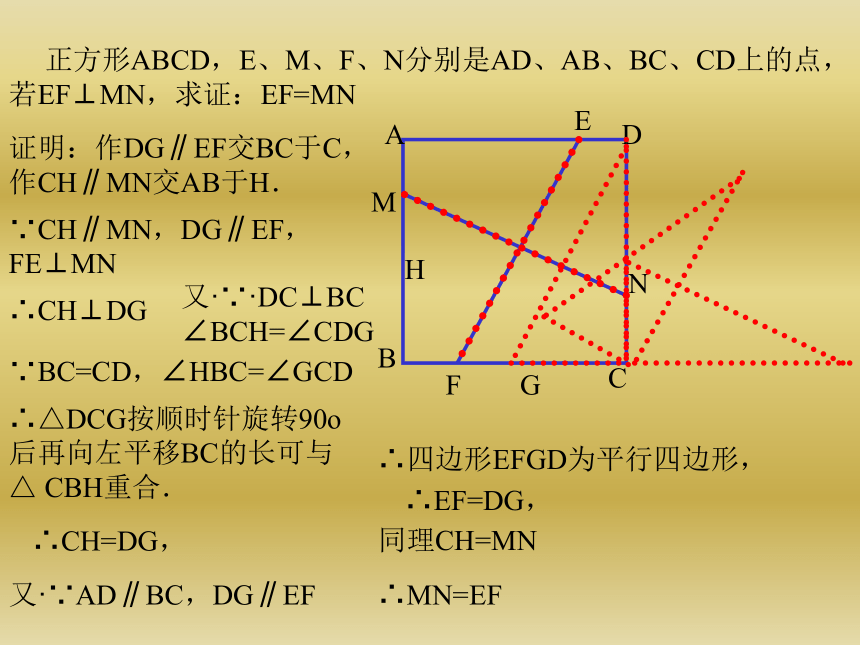
∠ADH=∠EHF=∠GKF=∠CDK又·∵∠ADH+∠AHD=90ο,∴∠AHD+∠EHF=90ο,∠DHF=90ο9:在等边三角形ABC中,p为△ABC内一点,PD∥AB,PF∥AC,PE∥BC,试说明:PD+PF+PE=AB解:延长FP交AB于G,延长DP交BC于H.∵ PD∥AB,PF∥AC,PE∥BC∴四边形AGPD与四边形EBHP都是平行四边形∴PD=AG,PH=BE∵△ABC是等边三角形∴∠PHF=∠B=60度∠PHF=∠C=60度∴△PHF为等边三角形,同理△PEG是等边三角形∴PE=EG,PH=PF=BE∴PD+PF+PE=AG+GE+EB=AB 对于平行四边形内任意一点P,问是否存在以AP,BP,CP,DP的长为边,且对角线的长恰好分别等于线段AB和BC的四边形?Q解:∵四边形ABCD是平行四边形∴AD∥BC,AD=BC,将△APD沿AB方向平移到△BQC的位置,连结PQ则PQ=AB,PQ=CD,BQ=AP,CQ=PD∴四边形BQCP的四条边分别为PA,PD,PC,PB,且两条对角线中的一条是BC,另一条是AB 已知六边形ABCDEF中,AB∥CD、BC∥EF、AF∥CD且AB-ED=EF-BC=CD-AF=3,求证:六边形的六个内角都是120ο证明:把边AB、BC沿AF方向平移AF的长度到折线F、G、N的位置,过D作EF的平行线交FG于M,交直线BG于H由平移的特征知.FG∥AB.FG=ABAF∥BG.AF=BGEF∥DM.EF=DM∴四边形DEFM是平行四边形∴DE∥FM.DE=FM∵AB-ED=EF-BC=CD-AF=3∴FG-FM=DM-DH=BH-BG=3同理:BH=CD. BC=DH∴GM=MH=GH=3∴△MGH是等边三角形∴∠MGH=60ο∴∠FAB=∠FGB=180ο-60ο=120ο同理可得六边形的其余各角也是120ο∴六边形的各角都是120οN 如图AA’=BB’=CC’=2,∠AOB’=∠BOC’=∠COA’=60ο、求证:S △AOB’ +S △BOC’ + S △COA’ <边长为2的等边三角形的面积QP证明:把△BOC’沿BB’方向平移2个单位,同样将△A’OC沿AA’方向平移2个单位。∵OQ=OP=2, ∠Q=∠P=60ο且QR+PR=OC+OC’=2∴Q、R、P三点在一直线上, △OPQ为等边三角形∴ S △AOB’ +S △BOC’ + S △COA’ =S△POQ-S △ARB’∴ S △AOB’ +S △BOC’ + S △COA’ < S△POQ 如图AA’=BB’=CC’=2,∠AOB’=∠BOC’=∠COA’=60ο、求证:S △AOB’ +S △BOC’ + S △COA’ <边长为2的等边三角形的面积QPR(1)(2) 正方形ABCD,E、M、F、N分别是AD、AB、BC、CD上的点,若EF⊥MN,求证:EF=MNABCDEFMNGH
∴EF=DG,证明:作DG∥EF交BC于C,作CH∥MN交AB于H.∵CH∥MN,DG∥EF,FE⊥MN
∴CH⊥DG
又·∵·DC⊥BC
∠BCH=∠CDG∵BC=CD,∠HBC=∠GCD∴△DCG按顺时针旋转90ο
后再向左平移BC的长可与△ CBH重合.∴CH=DG,
又·∵AD∥BC,DG∥EF∴四边形EFGD为平行四边形,同理CH=MN∴MN=EF 则把△ECF先平移再旋转可与△AHE完全重合, 在正方形ABCD中,E是BC上一点,CF平分∠DCG,AE⊥EF,求证:AE=EF证明:在AB上截取AH=CE,连HE.∵AB=BC,AH=CE∴BH=BE∴∠BHE=∠BEH=45ο,∴∠AHE=180ο—45ο=135ο又CF平分∠DOG∴∠DCF=∠GCF=45ο∴∠ECF=90ο+45ο=135ο又∵∠HAE+∠AEB=90ο,
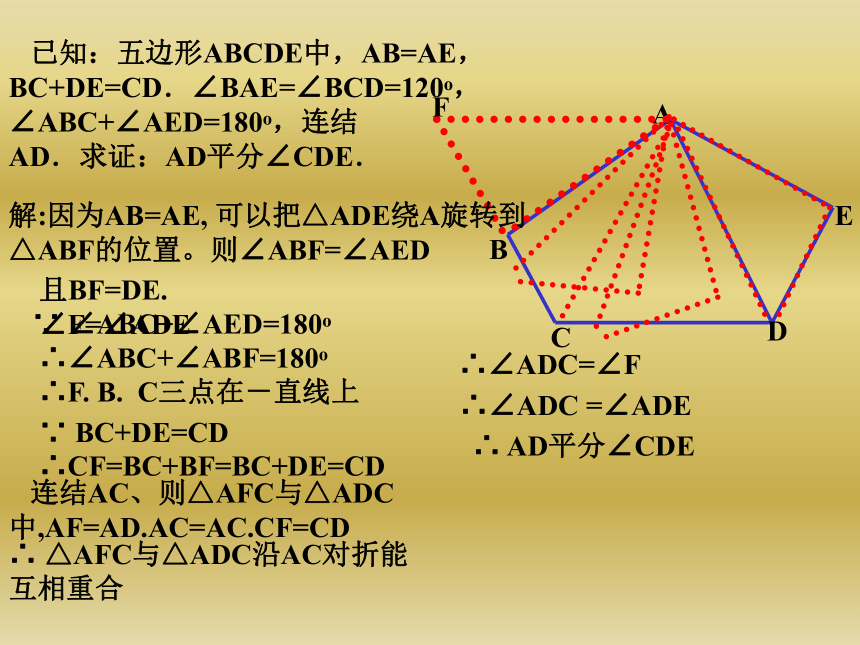
∠CEF十∠AEB=90ο∴∠HAE=∠CEF(同角的余角相等). 在△ECF与△AHE中,∴AH=EC,∠HAE=∠CEF,∠AHE=∠ECF=135ο∴AE=EF· 已知:五边形ABCDE中,AB=AE,BC+DE=CD.∠BAE=∠BCD=120ο,∠ABC+∠AED=180ο,连结
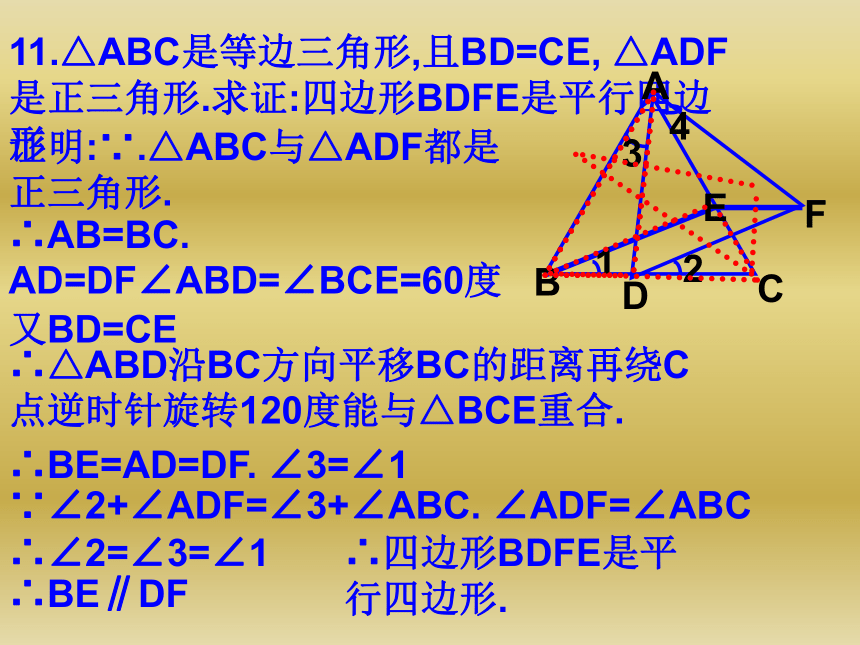
AD.求证:AD平分∠CDE.解:因为AB=AE, 可以把△ADE绕A旋转到△ABF的位置。则∠ABF=∠AED∵ ∠ABC+∠AED=180ο∴∠ABC+∠ABF=180ο∴F. B. C三点在-直线上且BF=DE. ∠F=∠ADE∵ BC+DE=CD∴CF=BC+BF=BC+DE=CD 连结AC、则△AFC与△ADC中,AF=AD.AC=AC.CF=CD∴ △AFC与△ADC沿AC对折能互相重合∴∠ADC=∠F ∴∠ADC =∠ADE∴ AD平分∠CDE 已知△ABC是边长为1的等边三角形, ∠BDC=120ο,BD=DC, ∠MDN=60ο求证:△AMN的周长等于2ABCMND证明:∵ ∠BDC=120ο,BD=DC, ∠MDN=60ο∴∠BDM+∠CDN=60ο, ∠DBC=∠DCB=30ο 把△BDM绕点D顺时针旋转120ο到△DCE的位置则.DM=DE,BM=CE, ∠BDM=∠CDE∴∠EDN=∠CDE+∠CDN=∠BDM+∠CDN=60ο∴∠MDN=∠EDN∴ A、C. E三点在-条直线上.△MDN沿DN时折能与△EDN重合∴MN=NE=CN+CE=CN+BM∴ :△AMN的周长=AM+MN+AN=AM+CN+BM+AN=AB+AC∵AB=AC=1∴ :△AMN的周长等于2∴∠DBM=30ο+60ο=90ο=∠DCN11.△ABC是等边三角形,且BD=CE, △ADF是正三角形.求证:四边形BDFE是平行四边形证明:∵.△ABC与△ADF都是正三角形.
∴AB=BC. AD=DF∠ABD=∠BCE=60度又BD=CE∴△ABD沿BC方向平移BC的距离再绕C点逆时针旋转120度能与△BCE重合.∴BE=AD=DF. ∠3=∠1∵∠2+∠ADF=∠3+∠ABC. ∠ADF=∠ABC∴∠2=∠3=∠1∴BE∥DF∴四边形BDFE是平行四边形. 在正方形ABCD中,P、Q分别为BC、CD上的点
(1)若∠PAQ=45ο,求证:PQ=PB+DQ
(2)若△PCQ的周长等于正方形周长的一半,求证:∠PAQ=45ο.32PQ证明(2)延长CB到E,使BE=DQ,连结AE由(1)知AE=AQ, ∠1=∠2∵△PCQ的周长等于正方形周长的一半∴PC+CQ+PQ=BC+CD即PQ=BP+DQ又∵DQ=BE∴PQ=BP+BE=EP∴△AEP沿AP对折后可与△AQP重合∴∠EAP=∠QAP又∵∠1=∠2, ∠BAQ+∠2=90ο∴∠1+∠BAQ=90ο∴∠EAQ=90ο∴∠PAQ=∠EAP=90ο÷2=45ο 操作:将一把三角尺放在正方形ABCD上,并使它的直角顶点P
在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.探究:(1)当点Q在DC上时,线段PQ与线段PB之间有怎样的大小关系?试说明你观察到的结论;(2)当点Q在DC的延长线上时,(1)中你观察到的结论还成立吗?说明理由。正图12~74中(1)供操作用,(2)、(3)供说明用]ABCDABCDABCDPPQQ 5.在四边形ABCD中,∠ADC=∠ABC=90ο,AD=CD,DP⊥AB于P,若四边形ABCD的面积为25.求DP的长解:∵ ∠ADC=∠ABC=90ο,AD=CD∴把△APD绕点D时针旋转90ο可到△DCE位置。∠PDE=∠PDC+∠EDC=∠PDC+∠ADP=∠ADC=90ο∵ DP⊥AB∴四边形PBED是矩形∵PD=DE∴四边形PBED是正方形∵四边形ABCD的面积为25∴S正方形DPBE =S四DPBC +S △DCE
= S四DPBC +S △APD =S四边形ABCD =25∵ S正方形DPBE =DP2∴DP=5在正方形ABCD中,E.F分别是BC.CD上的点且∠EAF=45οAG⊥EF于G.求证:AB=AGABCD1EFG证明:∵正方形ABC中,AB=AD,∠D=∠ABC=90ο,∠EAF=45ο∴∠1+∠3=90ο-45ο=45ο3 把△ADF顺时针旋转90ο到△ABH的位置.则∠ABH+∠ABC=∠D+∠ABC=180ο∴H.B.E三点在一直线上且AH=AF,AE=AE, ∠2+∠3=∠1+∠3=45ο=∠EAF∴把△AHE沿AE对折能与△AEF重合∵ AG⊥EF, ∠ABC=90ο∴AB=AG 一块在电脑屏幕上出现的矩形色块图,由六个不同颜色的正方形组成,设中间最小的正方形边长为a,求整个矩形色块的面积.解:设黑色正方形的边长为x、红色正方形的边长为y.则绿色正方形的边长为x+a,紫黄二色正方形的边长都是x-a,根据矩形对边相等得等式.x+2(x-a)=(x+a)+y (1)x+(x+a)=(x-a)+y (2)(1) -(2)得:x=5a,y=7a∴矩形色块的长为:13a、宽为11a。∴矩形色块的面积是:13a×11a=143a2 在一个边长不超过8cm的大正方形中,放入红.蓝.黄三张面积均为20cm2的正方形纸片,这个大正方形被三张纸片盖住的面积是44cm2,问大正方形的面积是多少? 所以x2即大正方形的面积为51.2cm2.解:把红色纸片沿大正方形上边线向左平移,直到红正方形的左边线与大正方形的左边线重合为止. 设大正方形的边长为xcm,放人的三张正方形的纸片边长为acm,根据题意,得ax+a(x—a)=44即2ax-a2=44·.因为a2=20,所以2ax=64所以ax=32,所以a2x2=322 正方形ABCD的对角线AC、BD相交于O,M是OB上一点,DG⊥CM于G,DG交OC于N,请猜测四边形MBCN是什么形状的四边形,并说明理由.解:四边形MBCN是等腰梯形∵正方形ABCD的对角线AC、BD相交于O∴∠4=∠5=90ο, ∠OBC=45ο,OC=OD=OB∵ DG⊥CM∴∠1+∠3=90ο, ∠2+∠3=90ο∴∠1=∠2∴△MOC绕点O逆时针旋转90ο后可与△DON重合∴OM=ON∴△OMN是等腰直角三角形. ∠OMN=∠OBC=45ο∴OB-OM=OC-ON即BM=CN∴MN∥BC,显然BM不平行于CN∴四边形MBCN是等腰梯形
3.已知正方形ABCD,E为BC上任意点,延长AB至F,使BF=BE,AE的延长线交CF于G.求证:AG⊥CF.证明:∵正方形ABCD∴BC=AB,∠ABC=∠CBF=90ο又∵ BF=BE∴△BCF绕点B逆时针旋转90后能与△ABF重合1234∴∠1=∠4∵∠2=∠3∠1+∠2=90ο∴∠3+∠4=90ο∴∠CGF=90ο∴ AG⊥CF 正方形ABCD中,E为CD中点,F为CE中点(AF=5/4AB),试问:∠BAF=2∠DAE吗?为什么?AGFEDCB5解: ∠BAF=2∠DAE、理由如下:作∠BAF的平分线交BC于G、交DC延长线于H∵AB∥CD、∠1=∠2∴∠H=∠1=∠2∴AF=FH设正方形的边长为4a、由题意有DE=EC=2a,EF=FC=a, FH=AF=5a,CH=4a=AB在△ABG与△HCG中,AB=CH, ∠B=∠BCH, ∠3=∠4∴ △ABG绕点G旋转180ο后能与△HCG重合∴BG=GC=2a=DE连结AC、则△ADE沿AC对折能与△ABG重合∴∠1=∠5∴∠BAF=∠1+∠2=2∠1=2∠5=2∠DAE △ABC的∠BAC=120ο,以BC为边向形外作等边△BCD,把△ABD绕D点按顺时针方向旋转60ο到△ECD的位置.若AB=3.AC=2.求∠BAD的度数和线段AD的长.解:∵等边△BCD∴∠4=∠6=60ο,由旋转的特征知:CE=AB=3,AD=DE, ∠5=∠1+∠4, ∠ADE=60ο∴∠2+∠6+∠5=∠2+60ο+∠1+∠4=∠1+∠2+120ο∵ ∠BAC=120ο∴∠2+∠6+∠5=∠1+∠2+∠BAC=180ο∴A、C、E三点在一直线上。∴△ADE是等边三角形.∴∠3=60ο,AD=AE∴∠BAD=∠BAC-∠3=120ο-60ο=60ο∴AE=AC+CE=2+3=5∵AC=2 △ABC的∠BAC=120ο,以BC为边向形外作等边△BCD,把△ABD绕D点按顺时针方向旋转60ο到△ECD的位置.若AB=3.AC=2.求∠BAD的度数和线段AD的长. 在正方形ABCD的中间有一个圆,其圆心是正方形对角线的交点O,E为圆上任意一点,请在圆上逆时针顺次再取三点F、G.H,连结AG、BH、DF,把正方形中的圆外部分分成形状、大小相同的四块.解:过E作圆的直径EG,再画垂直于直径的另一条直径FH,连结AG,BH.CE.DF就把正方形中的圆外部分分成形状、大小相同的四块. 已知:正方形ABCD中、对角线AC、BD交于O;又正方形OB’C’D’绕点O转动,问两个正方形重叠部分的面积如何变化?解:两个正方形重叠部分的面积不变、理由如下:∵正方形ABCD与正方形OB’C’D’中∴OD=OC, ∠EDO=∠OCF=45ο∠EOD+∠DOF=∠COF+∠DOF=90ο∴∠EOD=∠COF∴△DOE绕O旋转90ο能与△COF合S四OFDE =S△EOD+S△DOF=S△COF+S△DOF=S△COD=S正方形ABCD的四分之一解:因为四边形ABCD是平行四边形,所以AB=CD,BC=AD,∠ABC=∠ADC. 因为,△ABF和△ADE都是等边三角形,所以AB=BF,AD=DE,∠ABF=∠ADE=60度 所以△CEF是等边三角形. 所以:CD=BF.DE=BC.∠CDE=∠FBC 因此△CDE可先平移到点B再旋转可与△CBF重合所以CE=CF. 同理可得CE=EF 则把△ECF以AF的中点为中心,旋转90ο后可与△AHE完全重合, 在正方形ABCD中,E是BC上一点,CF平分∠DCG,AE⊥EF,求证:AE=EF证明:在AB上截取AH=CE,连HE.∵AB=BC,AH=CE∴BH=BE∴∠BHE=∠BEH=45ο,∴∠AHE=180ο—45ο=135ο又CF平分∠DOG∴∠DCF=∠GCF=45ο∴∠ECF=90ο+45ο=135ο又∵∠HAE+∠AFB=90ο,AF⊥EF,
∠CEF十∠AEB=90ο∴∠HAF=∠CEF(同角的余角相等). 在△ECF与△AHE中,∴AH=EC,∠HAE=∠CEF,∠AHE=∠ECF=135ο∴AE=EF·a2 如图:是一块长方形的菜地, 长为21米.宽为15米 在菜地上有一条宽为1米的小道,长方形的菜地上除小道外长满青菜。求长菜部分的面积为多少?解:长菜部分的面积为:(21-1)×15=300(平方米) 如图:是一块长方形的菜地, 长为21米.宽为15米 在菜地上有一条宽为1米的小道,长方形的菜地上除小道外长满青菜。求长菜部分的面积为多少?C △ABC中, ∠ACB=90ο,L.M.N在△ABC的三边上,CK⊥AB于K,求证:LN+NM+ML>2KC证明:做△ABC关于BC边的轴对称图形△BCD,再做△BCD关于CD的轴对称图形△DEC,则△ABC与△DEC关于点C成中心对称,高CK关于点C的对称线段是CH.CL关于点C的对称线段是CR 由轴对称的意义可做出△LMN关于BC的对称△PQM, △PQM关于CD的轴对称图形△QSR∴△LMN的周长=LN+MN+ML>2KC=LM+MQ+QR>2CL∵直角三角形KCL中.CL>KC∴△LMN的周长=LN+MN+ML 在等边三角形ABC中,P为AB的中点,Q为AC中点,R为BC中点,M是RC上任一点,且△PMS是等边三角形.求证:RM=QS证明:连结PQ,PR∵等边三角形ABC中,PQ,PR是两条中位线∴PQ=PR, ∠2+∠3=60ο∵△PMS是等边三角形∴∠2+∠4=60ο,PS=PM∴∠3=∠4∴△PQS绕点P顺时针旋转60ο可与△PRM重合∴RM=QS △ABC中, ∠C=90ο, ∠A=30ο, △ABE和△ACD都是等边三角形.求证:EF=FD12FDECBA证明:过E作EH⊥AB于H∴ ∠1=30ο=∠3AB=BE∠ACB=∠EHB=90ο∴△EBH绕B顺时针旋转60ο与△ABC重合∴EH=AC=AD∵∠FAD=∠1+∠2=90ο=∠EHF∠EFH=∠AFD∴△EHF绕F旋转180ο能与△ADF重合∴EF=FD M是△ABC钭边AB的中点,D是AC边上一点,CD=BM,DM与CB的延长线交于E证明:连CM,作CN⊥DE于N∵∠ACB=90ο,AM=BM∴CM=AM=BM又CD=BM∴CD=CM又CN⊥DE∴∠1=∠2∵∠1+∠NCE=90ο, ∠E+∠NCE=90ο∴∠1=∠E=∠2∴∠1+∠2=2∠E∴∠A=∠ACM=∠1+∠2∴∠A=2∠E △ABC中,AC=BC,∠ACB=90ο,AD=AC, ∠CAD=30ο,求证:BD=CD证明:作△ACD关于CD的对称△A’CD,连结A’B∵AD=AC,∴AD=AC=CA’=A’D∴四边形ACA’D是菱形∵∠ACB=90ο, ∠CAD=30ο∴∠A’CB=60ο又BC=CA=CA’∴△A’BC是等边三角形∴A’B=A’C=A’D∴∠BA’D=60ο-30ο=30ο∴∠DBA’=(180ο-30ο) ÷2=75ο∴∠DBC=15ο同理∠DCB=15ο∴BD=CD△ABC中, ∠A=90ο,AB=AC,BD平分∠ABC,CE⊥BD证明:延长CE交BA延长线于H∵BD平分∠ABC,CE⊥BD∴沿BE对折△BCE与△BHE互相重合∵∠ABD+∠H=90ο∠ACH+∠H=90ο∴∠ABD=∠ACH∵∠BAD=∠HACAB=AC∴△ACH绕点A顺时针旋转90ο与△ABD互相重合 △ABC中,AB=AC, ∠BAC=80ο, ∠PBC=10ο, ∠PCB=30ο,求∠BAP的度数 作∠BAC的平分线与CP延长线交于D,连BD∠BAD=40ο, ∠DPB=40ο △ABD沿AD对折与△ACD重合∠ABD=∠ACD=20ο∠DBP=50ο-20ο-10ο=20ο△ABD沿BD对折与△BPD互相重合AD=DP∠ADC=120ο∠BAP=40ο+30ο=70ο △ABC中,AB>AC,作∠FBC=∠ECB= ∠A,求证:BE=CF1在△MCF内作∠2=∠1△BEM沿BC的中垂线对折互相重合BE=CG∠FGC=∠FBC+∠BCG=∠A+∠2=∠A+∠1∠GFC=∠A+∠1∠GFC=∠FGCCF=CG=BE 三角形ABC中,BC=AC, ∠ACB=90ο,AD=DC,CE⊥BD交BD于E,求证:∠BDC=∠ADF过A作AC的垂线交CF延长线于G △BCD先平移再旋转后与△ACG重合∠BDC=∠AGCAD=DC=AG∠GAF=∠DAF=45ο△AGF沿AF对折与△ADF重合∠BDC=∠AGF=ADF △ABC中, ∠B=60ο, ∠A. ∠C的平分线相交于O,求证:DC+AE=AC∠AOE=∠COD=60ο∠AOC=120ο作∠AOC的平分线OH △AOE沿OA对折与△AOH重合, △COD沿OC对折与△COH重合AE+DC=AH+HC=ACEFADCB 正方形ABCD中,E是AD的中点,求证:AF⊥BE 作正方形的对称轴EG,则沿EG对折△ABE与△DCE互相重合45∠4=∠5连结AC∠3+∠4=∠2+∠5=45ο∠2=∠3沿BD对折△AOF与△COF重合∠1=∠2=∠3∠3+∠BHO=90ο∠1+∠AHE=90οAF⊥BE △ABC是等边三角形,延长BC至D,延长BA至E,使AE=BD,连结CE.DE.求证:CE=DE证明:延长BD到F使DF=BC=AB,连结EF∵BE=AB+AE=BD+DF=BF∴BE=BF, ∠B=60ο,BC=DF∴△EBF为等边三角形∵BF=FE, ∠B=∠F=60ο,BC=DF∴△BCE沿BF边上的高对折能与△EDF重合∴CE=DE 平行四边形ABCD中,BC=2AB,M是AD中点,CE⊥AB,求证:∠DME=3∠AEM 取BC中点N,连结MN,连结CM并延长CM交BA延长线于G四边形MNCD是菱形 CM=MG,EM是直角三角形斜边的中线,EM=MC∠EMN=∠NMC=∠CMD∠DME=3∠EMN=3∠AEM △ABC中,BE、CD是角平分线,P是DE中点,PQ⊥BC,PM⊥AB,PN⊥AC.证:PQ=PM+PNPNMEDCBAQ 三角形ABC中, ∠BAC=120ο,求证:PA+PB+PC>AB+ACPCBA证明:把△APC绕A逆时针旋转60度到△AED位置,连PE∵∠BAC=120ο∴B、A、D三点在一直线上由两点之间线段最短得:PA+PB+PC=PE+BP+ED>AB+AD=AB+AC △ABC中,AD⊥BC, ∠A=45ο,BD=3,DC=2,求△ABC的面积DCBA解:分别以AB.AC为轴做出对称△AFC和△AEB,延长FC.EB交于点G,则四边形AFGE是正方形. 设AD=x则BG=3-x,在直角△BCG中(x-2)2+(x-3)2=(2+3)2解得x=6 △ABC中, ∠C=90ο,BM=AC,点N在AC上,且AN=MC.求证:∠BMP=45οPNMCBA11412113 已知:E.F分别是正方形ABCD的边BC.CD上的点,AE,AF分别与对角线BD交于M、N,若∠EAF=50ο,则∠CME+∠CNF=?∠CNF=∠1+∠3∠CME =∠2+∠4∠CME+∠CNF=∠2+∠4+∠1+∠3=2(∠1+∠2)=100οayxb 正方形被两条与边平行的线段EF.GH分割成四个小矩形,EF与GH交于P,若矩形PFCH的面积恰是矩形AGPE面积的2倍,求∠HAF=?a+b=x+y2ax=bya-x=y-b∴a2-2ax+x2=y2-2by+b2∴(a+x)2=y2+b2=FH2∴BF+DH=FH∴∠FAH=45ο P.Q为△ABC的边AB.AC上的两定点,在BC上取一点R,使△PQR的周长最短。解:作出P关于BC的对称点M,连结MQ,MQ交BC于R,则R就是所求作的点。解:作A关于EF的对称点C,连结BC交EF于点D,则按AD方向撞击黑球,必沿DB反弹击中白球B。 OA.OB表示两条小河,一游客在P点想先到河岸OA观景,再到河岸OB垂钓,最后回到P点,请你替这位游客画出可走的最短路线。P解:1、作点P关于OA.OB的对称点M,N、2.连结MN,MN交OA.OB于D.E两点。3.连结PD,PE、那么游客可走的最短路线是PD、DE、EP。 A.B.C是地面上不在同一直线上的三点,一只青蛙位于地面上的P点,第一步青蛙从P跳到P关于A的对称点P1,第二步青蛙从P跳到P关于A的对称点P2,第三步青蛙从P跳到P关于A的对称点P4…依此跳法类推,问青蛙跳完1999步,落在地面上什么位置上?解:青蛙每跳一次,就完成一个中心对称变换,由中位线定理得:PP2∥2AB∥P3P5, PP2=2AB=P3P5, 并且由P2C=CP3,P6C=CP5,知四边形P3P5P2P6是平行四边形则:P2P6∥P2P, P2P6=P2P 因为1999被6除余1,故青蛙跳完第1999步后,应落在P1位置. BD.CE是三角形ABC的高,点P在BD的延长线上,BP=AC,Q在CE上,CQ=AB,求证(1)AP=AQ,(2)AP⊥AQ12证明:∵ BD.CE是三角形ABC的高∴∠1+∠BAC=90ο, ∠2+∠BAC=90ο∵∠1=∠2∵AB=CQ,BP=AC∴△AQC经平移与旋转后与△ABP互相重合∴AP=AQ, ∠AQC=∠BAC∵∠AQC=∠3+90ο∠BAP=∠3+∠PAQ∴∠3+90ο=∠3+∠PAQ∴∠PAQ=90ο 四边形ABCD中,AC平分∠BAD,并且AB+AD=2AE,求:∠ABC+∠ADC=?DCBA解:作CE⊥AB于E,作CF⊥AD交AD延长线于F∵AC平分∠BAD∴CE=CF,AE=AF=AD+DF∵AB+AD=2AE∴AE+EB+AD=2AE∴AE=AD+EB∴AD+DF=AD+EB∴DF=EB △CBE绕点C旋转后能与△CDF重合22、如图,正三角形ABC边长是1,点O是正三角形ABC的中心,∠MON=1200在∠MON绕着点O旋转过程中
(1)观察∠MON与正三角形ABC围成的四边形POQC的面积是否保持不变? (2)观察CP+CQ的长度是否发生变化? 对于初学者,应先从特殊情况入手。对于图(1),显然四边形POQC 退化为△BOC,面积是正三角形ABC面积的1/3对于图(2),连结OA.OC,则S四边形POQC
=S △QOC + S△POC =S △AOP+ S△POC = S△AOC四边形POQC 面积是正三角形ABC面积的1/3 对于图(3),猜测四边形POQC 面积是正三角形ABC面积的1/3N2、如图,正三角形ABC边长是1,点O是正三角形ABC的中心,∠MON=1200在∠MON绕着点O旋转过程中
(1)观察∠MON与正三角形ABC围成的四边形POQC的面积是否保持不变? (2)观察CP+CQ的长度是否发生变化?解:四边形POQC的面积和CP+CQ的长度都没有发生变化。有已知知:OA=OC∠AOP+ ∠POC=1200∠COQ+ ∠POC=1200∴∠AOP=∠QOC又∠OAP=∠QCO=300∴ △AOP绕O旋转1200后能与△COQ重合∴ S四边形POQC=S △QOC + S△POC =S △AOP+ S△POC = S△AOC四边形POQC 面积是正三角形ABC面积的1/3∴CP+CQ=AP+CP=AC=1旋转的应用 右图正方形KMLN的一个顶点K与正方形ABCD的中心重合,当正方形KMLN绕K运动时,两正方形重叠部分KHBG的面积如何变化? 结论:始终为正方形ABCD面积的四分之一2、如图,正三角形ABC边长是1,点O是正三角形ABC的中心,∠MON=1200在∠MON绕着点O旋转过程中
(1)观察∠MON与正三角形ABC围成的四边形POQC的面积是否保持不变? (2)观察CP+CQ的长度是否发生变化?对于图(2),连结OA.OC,则S四边形POQC
=S △QOC + S△POC =S △AOP+ S△POC = S△AOC四边形POQC 面积是正三角形ABC面积的1/3 对于图(3),猜测四边形POQC 面积是正三角形ABC面积的1/32、如图,正三角形ABC边长是1,点O是正三角形ABC的中心,∠MON=1200在∠MON绕着点O旋转过程中
(1)观察∠MON与正三角形ABC围成的四边形POQC的面积是否保持不变? (2)观察CP+CQ的长度是否发生变化? 对于初学者,应先从特殊情况入手。对于图(1),显然四边形POQC 退化为△BOC,面积是正三角形ABC面积的1/3对于图(2),连结OA.OC,则S四边形POQC
=S △QOC + S△POC =S △AOP+ S△POC = S△AOC四边形POQC 面积是正三角形ABC面积的1/3 对于图(3),猜测四边形POQC 面积是正三角形ABC面积的1/3N 在矩形草地ABCD中,横向阴影部分是矩形道路,另一阴影部分是平行四边形道路。依照图中标注的数据,计算空白部分(长草部分)的面积。ccabccab分析:先将图(1)中的平行四边形M变为图(2)中得矩形N,长草部分的面积不变。再将横向矩形向下平移,这样长草部分的面积就变成了一个长为a-c,宽为b-c的矩形。(1)(2)MN 解:S阴影 =BC ×AB ABDC=(a - c) ×( b - c)=ab – ac – bc + c2 一漆匠用右图所示的胶滚沿从左到右的方向将图案滚涂到墙上,下列给出的四个图案中,符合图示胶滚涂出的图案是( )
∴BE=BH
=BG+GH
=BG+FC∴ ∠H=∠AGE,GH=FC,GH=FC
∵∠AGE+∠GAE=90ο, ∠AEB+∠GAE=90ο∴∠AEB=∠AGE=∠H, ∠ABE=∠CBH=90ο又∵AB=BC,∴△ABE绕B点旋转90ο可与△CBH重合
EF 4. 在线段AE上取一点B,使AB>BE,以AB,BE为边在AE同侧作正方形ABCD和BEFG,在AB上取AH=BE,在BC的延长线上取一点K,使CK=BG,求证:四边形HFKD为正方形.∴四边形DHFK为正方形.证明:四边形ABCD和BEFG均是正方形,∴AB=BC=CD=DA,BE=EF=FG=GB.
又·∵AH=BE,·CK=BG∴AH=EF=GF=CK,AD=HE=KG=CD,∠DAH=∠HEF=∠KGF=∠DCK=90ο 则△DAH, △HEF,△KGF,△DCK,经过平移、旋转都能完全重合∴DH=HF=KF=DK,
∠ADH=∠EHF=∠GKF=∠CDK又·∵∠ADH+∠AHD=90ο,∴∠AHD+∠EHF=90ο,∠DHF=90ο9:在等边三角形ABC中,p为△ABC内一点,PD∥AB,PF∥AC,PE∥BC,试说明:PD+PF+PE=AB解:延长FP交AB于G,延长DP交BC于H.∵ PD∥AB,PF∥AC,PE∥BC∴四边形AGPD与四边形EBHP都是平行四边形∴PD=AG,PH=BE∵△ABC是等边三角形∴∠PHF=∠B=60度∠PHF=∠C=60度∴△PHF为等边三角形,同理△PEG是等边三角形∴PE=EG,PH=PF=BE∴PD+PF+PE=AG+GE+EB=AB 对于平行四边形内任意一点P,问是否存在以AP,BP,CP,DP的长为边,且对角线的长恰好分别等于线段AB和BC的四边形?Q解:∵四边形ABCD是平行四边形∴AD∥BC,AD=BC,将△APD沿AB方向平移到△BQC的位置,连结PQ则PQ=AB,PQ=CD,BQ=AP,CQ=PD∴四边形BQCP的四条边分别为PA,PD,PC,PB,且两条对角线中的一条是BC,另一条是AB 已知六边形ABCDEF中,AB∥CD、BC∥EF、AF∥CD且AB-ED=EF-BC=CD-AF=3,求证:六边形的六个内角都是120ο证明:把边AB、BC沿AF方向平移AF的长度到折线F、G、N的位置,过D作EF的平行线交FG于M,交直线BG于H由平移的特征知.FG∥AB.FG=ABAF∥BG.AF=BGEF∥DM.EF=DM∴四边形DEFM是平行四边形∴DE∥FM.DE=FM∵AB-ED=EF-BC=CD-AF=3∴FG-FM=DM-DH=BH-BG=3同理:BH=CD. BC=DH∴GM=MH=GH=3∴△MGH是等边三角形∴∠MGH=60ο∴∠FAB=∠FGB=180ο-60ο=120ο同理可得六边形的其余各角也是120ο∴六边形的各角都是120οN 如图AA’=BB’=CC’=2,∠AOB’=∠BOC’=∠COA’=60ο、求证:S △AOB’ +S △BOC’ + S △COA’ <边长为2的等边三角形的面积QP证明:把△BOC’沿BB’方向平移2个单位,同样将△A’OC沿AA’方向平移2个单位。∵OQ=OP=2, ∠Q=∠P=60ο且QR+PR=OC+OC’=2∴Q、R、P三点在一直线上, △OPQ为等边三角形∴ S △AOB’ +S △BOC’ + S △COA’ =S△POQ-S △ARB’∴ S △AOB’ +S △BOC’ + S △COA’ < S△POQ 如图AA’=BB’=CC’=2,∠AOB’=∠BOC’=∠COA’=60ο、求证:S △AOB’ +S △BOC’ + S △COA’ <边长为2的等边三角形的面积QPR(1)(2) 正方形ABCD,E、M、F、N分别是AD、AB、BC、CD上的点,若EF⊥MN,求证:EF=MNABCDEFMNGH
∴EF=DG,证明:作DG∥EF交BC于C,作CH∥MN交AB于H.∵CH∥MN,DG∥EF,FE⊥MN
∴CH⊥DG
又·∵·DC⊥BC
∠BCH=∠CDG∵BC=CD,∠HBC=∠GCD∴△DCG按顺时针旋转90ο
后再向左平移BC的长可与△ CBH重合.∴CH=DG,
又·∵AD∥BC,DG∥EF∴四边形EFGD为平行四边形,同理CH=MN∴MN=EF 则把△ECF先平移再旋转可与△AHE完全重合, 在正方形ABCD中,E是BC上一点,CF平分∠DCG,AE⊥EF,求证:AE=EF证明:在AB上截取AH=CE,连HE.∵AB=BC,AH=CE∴BH=BE∴∠BHE=∠BEH=45ο,∴∠AHE=180ο—45ο=135ο又CF平分∠DOG∴∠DCF=∠GCF=45ο∴∠ECF=90ο+45ο=135ο又∵∠HAE+∠AEB=90ο,
∠CEF十∠AEB=90ο∴∠HAE=∠CEF(同角的余角相等). 在△ECF与△AHE中,∴AH=EC,∠HAE=∠CEF,∠AHE=∠ECF=135ο∴AE=EF· 已知:五边形ABCDE中,AB=AE,BC+DE=CD.∠BAE=∠BCD=120ο,∠ABC+∠AED=180ο,连结
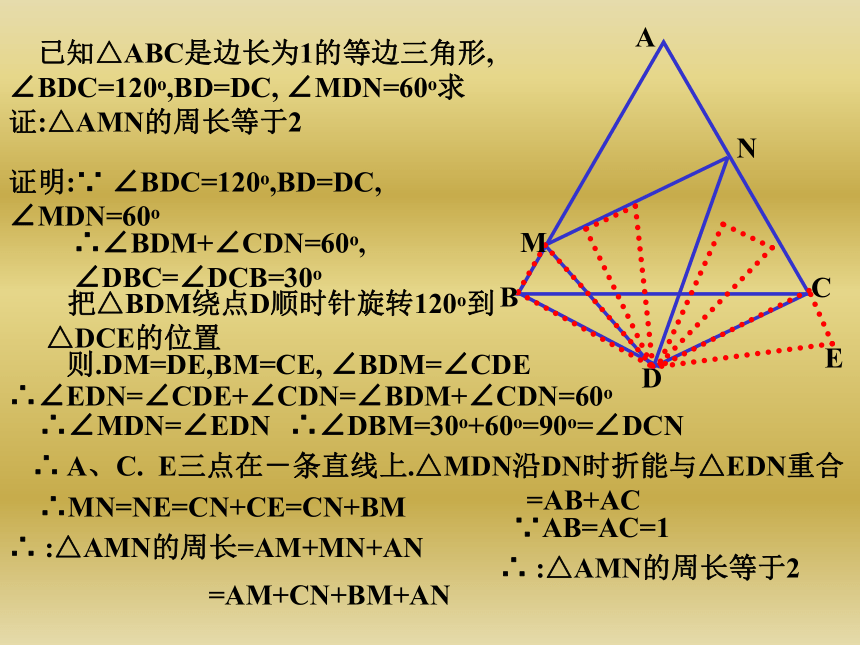
AD.求证:AD平分∠CDE.解:因为AB=AE, 可以把△ADE绕A旋转到△ABF的位置。则∠ABF=∠AED∵ ∠ABC+∠AED=180ο∴∠ABC+∠ABF=180ο∴F. B. C三点在-直线上且BF=DE. ∠F=∠ADE∵ BC+DE=CD∴CF=BC+BF=BC+DE=CD 连结AC、则△AFC与△ADC中,AF=AD.AC=AC.CF=CD∴ △AFC与△ADC沿AC对折能互相重合∴∠ADC=∠F ∴∠ADC =∠ADE∴ AD平分∠CDE 已知△ABC是边长为1的等边三角形, ∠BDC=120ο,BD=DC, ∠MDN=60ο求证:△AMN的周长等于2ABCMND证明:∵ ∠BDC=120ο,BD=DC, ∠MDN=60ο∴∠BDM+∠CDN=60ο, ∠DBC=∠DCB=30ο 把△BDM绕点D顺时针旋转120ο到△DCE的位置则.DM=DE,BM=CE, ∠BDM=∠CDE∴∠EDN=∠CDE+∠CDN=∠BDM+∠CDN=60ο∴∠MDN=∠EDN∴ A、C. E三点在-条直线上.△MDN沿DN时折能与△EDN重合∴MN=NE=CN+CE=CN+BM∴ :△AMN的周长=AM+MN+AN=AM+CN+BM+AN=AB+AC∵AB=AC=1∴ :△AMN的周长等于2∴∠DBM=30ο+60ο=90ο=∠DCN11.△ABC是等边三角形,且BD=CE, △ADF是正三角形.求证:四边形BDFE是平行四边形证明:∵.△ABC与△ADF都是正三角形.
∴AB=BC. AD=DF∠ABD=∠BCE=60度又BD=CE∴△ABD沿BC方向平移BC的距离再绕C点逆时针旋转120度能与△BCE重合.∴BE=AD=DF. ∠3=∠1∵∠2+∠ADF=∠3+∠ABC. ∠ADF=∠ABC∴∠2=∠3=∠1∴BE∥DF∴四边形BDFE是平行四边形. 在正方形ABCD中,P、Q分别为BC、CD上的点
(1)若∠PAQ=45ο,求证:PQ=PB+DQ
(2)若△PCQ的周长等于正方形周长的一半,求证:∠PAQ=45ο.32PQ证明(2)延长CB到E,使BE=DQ,连结AE由(1)知AE=AQ, ∠1=∠2∵△PCQ的周长等于正方形周长的一半∴PC+CQ+PQ=BC+CD即PQ=BP+DQ又∵DQ=BE∴PQ=BP+BE=EP∴△AEP沿AP对折后可与△AQP重合∴∠EAP=∠QAP又∵∠1=∠2, ∠BAQ+∠2=90ο∴∠1+∠BAQ=90ο∴∠EAQ=90ο∴∠PAQ=∠EAP=90ο÷2=45ο 操作:将一把三角尺放在正方形ABCD上,并使它的直角顶点P
在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.探究:(1)当点Q在DC上时,线段PQ与线段PB之间有怎样的大小关系?试说明你观察到的结论;(2)当点Q在DC的延长线上时,(1)中你观察到的结论还成立吗?说明理由。正图12~74中(1)供操作用,(2)、(3)供说明用]ABCDABCDABCDPPQQ 5.在四边形ABCD中,∠ADC=∠ABC=90ο,AD=CD,DP⊥AB于P,若四边形ABCD的面积为25.求DP的长解:∵ ∠ADC=∠ABC=90ο,AD=CD∴把△APD绕点D时针旋转90ο可到△DCE位置。∠PDE=∠PDC+∠EDC=∠PDC+∠ADP=∠ADC=90ο∵ DP⊥AB∴四边形PBED是矩形∵PD=DE∴四边形PBED是正方形∵四边形ABCD的面积为25∴S正方形DPBE =S四DPBC +S △DCE
= S四DPBC +S △APD =S四边形ABCD =25∵ S正方形DPBE =DP2∴DP=5在正方形ABCD中,E.F分别是BC.CD上的点且∠EAF=45οAG⊥EF于G.求证:AB=AGABCD1EFG证明:∵正方形ABC中,AB=AD,∠D=∠ABC=90ο,∠EAF=45ο∴∠1+∠3=90ο-45ο=45ο3 把△ADF顺时针旋转90ο到△ABH的位置.则∠ABH+∠ABC=∠D+∠ABC=180ο∴H.B.E三点在一直线上且AH=AF,AE=AE, ∠2+∠3=∠1+∠3=45ο=∠EAF∴把△AHE沿AE对折能与△AEF重合∵ AG⊥EF, ∠ABC=90ο∴AB=AG 一块在电脑屏幕上出现的矩形色块图,由六个不同颜色的正方形组成,设中间最小的正方形边长为a,求整个矩形色块的面积.解:设黑色正方形的边长为x、红色正方形的边长为y.则绿色正方形的边长为x+a,紫黄二色正方形的边长都是x-a,根据矩形对边相等得等式.x+2(x-a)=(x+a)+y (1)x+(x+a)=(x-a)+y (2)(1) -(2)得:x=5a,y=7a∴矩形色块的长为:13a、宽为11a。∴矩形色块的面积是:13a×11a=143a2 在一个边长不超过8cm的大正方形中,放入红.蓝.黄三张面积均为20cm2的正方形纸片,这个大正方形被三张纸片盖住的面积是44cm2,问大正方形的面积是多少? 所以x2即大正方形的面积为51.2cm2.解:把红色纸片沿大正方形上边线向左平移,直到红正方形的左边线与大正方形的左边线重合为止. 设大正方形的边长为xcm,放人的三张正方形的纸片边长为acm,根据题意,得ax+a(x—a)=44即2ax-a2=44·.因为a2=20,所以2ax=64所以ax=32,所以a2x2=322 正方形ABCD的对角线AC、BD相交于O,M是OB上一点,DG⊥CM于G,DG交OC于N,请猜测四边形MBCN是什么形状的四边形,并说明理由.解:四边形MBCN是等腰梯形∵正方形ABCD的对角线AC、BD相交于O∴∠4=∠5=90ο, ∠OBC=45ο,OC=OD=OB∵ DG⊥CM∴∠1+∠3=90ο, ∠2+∠3=90ο∴∠1=∠2∴△MOC绕点O逆时针旋转90ο后可与△DON重合∴OM=ON∴△OMN是等腰直角三角形. ∠OMN=∠OBC=45ο∴OB-OM=OC-ON即BM=CN∴MN∥BC,显然BM不平行于CN∴四边形MBCN是等腰梯形
3.已知正方形ABCD,E为BC上任意点,延长AB至F,使BF=BE,AE的延长线交CF于G.求证:AG⊥CF.证明:∵正方形ABCD∴BC=AB,∠ABC=∠CBF=90ο又∵ BF=BE∴△BCF绕点B逆时针旋转90后能与△ABF重合1234∴∠1=∠4∵∠2=∠3∠1+∠2=90ο∴∠3+∠4=90ο∴∠CGF=90ο∴ AG⊥CF 正方形ABCD中,E为CD中点,F为CE中点(AF=5/4AB),试问:∠BAF=2∠DAE吗?为什么?AGFEDCB5解: ∠BAF=2∠DAE、理由如下:作∠BAF的平分线交BC于G、交DC延长线于H∵AB∥CD、∠1=∠2∴∠H=∠1=∠2∴AF=FH设正方形的边长为4a、由题意有DE=EC=2a,EF=FC=a, FH=AF=5a,CH=4a=AB在△ABG与△HCG中,AB=CH, ∠B=∠BCH, ∠3=∠4∴ △ABG绕点G旋转180ο后能与△HCG重合∴BG=GC=2a=DE连结AC、则△ADE沿AC对折能与△ABG重合∴∠1=∠5∴∠BAF=∠1+∠2=2∠1=2∠5=2∠DAE △ABC的∠BAC=120ο,以BC为边向形外作等边△BCD,把△ABD绕D点按顺时针方向旋转60ο到△ECD的位置.若AB=3.AC=2.求∠BAD的度数和线段AD的长.解:∵等边△BCD∴∠4=∠6=60ο,由旋转的特征知:CE=AB=3,AD=DE, ∠5=∠1+∠4, ∠ADE=60ο∴∠2+∠6+∠5=∠2+60ο+∠1+∠4=∠1+∠2+120ο∵ ∠BAC=120ο∴∠2+∠6+∠5=∠1+∠2+∠BAC=180ο∴A、C、E三点在一直线上。∴△ADE是等边三角形.∴∠3=60ο,AD=AE∴∠BAD=∠BAC-∠3=120ο-60ο=60ο∴AE=AC+CE=2+3=5∵AC=2 △ABC的∠BAC=120ο,以BC为边向形外作等边△BCD,把△ABD绕D点按顺时针方向旋转60ο到△ECD的位置.若AB=3.AC=2.求∠BAD的度数和线段AD的长. 在正方形ABCD的中间有一个圆,其圆心是正方形对角线的交点O,E为圆上任意一点,请在圆上逆时针顺次再取三点F、G.H,连结AG、BH、DF,把正方形中的圆外部分分成形状、大小相同的四块.解:过E作圆的直径EG,再画垂直于直径的另一条直径FH,连结AG,BH.CE.DF就把正方形中的圆外部分分成形状、大小相同的四块. 已知:正方形ABCD中、对角线AC、BD交于O;又正方形OB’C’D’绕点O转动,问两个正方形重叠部分的面积如何变化?解:两个正方形重叠部分的面积不变、理由如下:∵正方形ABCD与正方形OB’C’D’中∴OD=OC, ∠EDO=∠OCF=45ο∠EOD+∠DOF=∠COF+∠DOF=90ο∴∠EOD=∠COF∴△DOE绕O旋转90ο能与△COF合S四OFDE =S△EOD+S△DOF=S△COF+S△DOF=S△COD=S正方形ABCD的四分之一解:因为四边形ABCD是平行四边形,所以AB=CD,BC=AD,∠ABC=∠ADC. 因为,△ABF和△ADE都是等边三角形,所以AB=BF,AD=DE,∠ABF=∠ADE=60度 所以△CEF是等边三角形. 所以:CD=BF.DE=BC.∠CDE=∠FBC 因此△CDE可先平移到点B再旋转可与△CBF重合所以CE=CF. 同理可得CE=EF 则把△ECF以AF的中点为中心,旋转90ο后可与△AHE完全重合, 在正方形ABCD中,E是BC上一点,CF平分∠DCG,AE⊥EF,求证:AE=EF证明:在AB上截取AH=CE,连HE.∵AB=BC,AH=CE∴BH=BE∴∠BHE=∠BEH=45ο,∴∠AHE=180ο—45ο=135ο又CF平分∠DOG∴∠DCF=∠GCF=45ο∴∠ECF=90ο+45ο=135ο又∵∠HAE+∠AFB=90ο,AF⊥EF,
∠CEF十∠AEB=90ο∴∠HAF=∠CEF(同角的余角相等). 在△ECF与△AHE中,∴AH=EC,∠HAE=∠CEF,∠AHE=∠ECF=135ο∴AE=EF·a2 如图:是一块长方形的菜地, 长为21米.宽为15米 在菜地上有一条宽为1米的小道,长方形的菜地上除小道外长满青菜。求长菜部分的面积为多少?解:长菜部分的面积为:(21-1)×15=300(平方米) 如图:是一块长方形的菜地, 长为21米.宽为15米 在菜地上有一条宽为1米的小道,长方形的菜地上除小道外长满青菜。求长菜部分的面积为多少?C △ABC中, ∠ACB=90ο,L.M.N在△ABC的三边上,CK⊥AB于K,求证:LN+NM+ML>2KC证明:做△ABC关于BC边的轴对称图形△BCD,再做△BCD关于CD的轴对称图形△DEC,则△ABC与△DEC关于点C成中心对称,高CK关于点C的对称线段是CH.CL关于点C的对称线段是CR 由轴对称的意义可做出△LMN关于BC的对称△PQM, △PQM关于CD的轴对称图形△QSR∴△LMN的周长=LN+MN+ML>2KC=LM+MQ+QR>2CL∵直角三角形KCL中.CL>KC∴△LMN的周长=LN+MN+ML 在等边三角形ABC中,P为AB的中点,Q为AC中点,R为BC中点,M是RC上任一点,且△PMS是等边三角形.求证:RM=QS证明:连结PQ,PR∵等边三角形ABC中,PQ,PR是两条中位线∴PQ=PR, ∠2+∠3=60ο∵△PMS是等边三角形∴∠2+∠4=60ο,PS=PM∴∠3=∠4∴△PQS绕点P顺时针旋转60ο可与△PRM重合∴RM=QS △ABC中, ∠C=90ο, ∠A=30ο, △ABE和△ACD都是等边三角形.求证:EF=FD12FDECBA证明:过E作EH⊥AB于H∴ ∠1=30ο=∠3AB=BE∠ACB=∠EHB=90ο∴△EBH绕B顺时针旋转60ο与△ABC重合∴EH=AC=AD∵∠FAD=∠1+∠2=90ο=∠EHF∠EFH=∠AFD∴△EHF绕F旋转180ο能与△ADF重合∴EF=FD M是△ABC钭边AB的中点,D是AC边上一点,CD=BM,DM与CB的延长线交于E证明:连CM,作CN⊥DE于N∵∠ACB=90ο,AM=BM∴CM=AM=BM又CD=BM∴CD=CM又CN⊥DE∴∠1=∠2∵∠1+∠NCE=90ο, ∠E+∠NCE=90ο∴∠1=∠E=∠2∴∠1+∠2=2∠E∴∠A=∠ACM=∠1+∠2∴∠A=2∠E △ABC中,AC=BC,∠ACB=90ο,AD=AC, ∠CAD=30ο,求证:BD=CD证明:作△ACD关于CD的对称△A’CD,连结A’B∵AD=AC,∴AD=AC=CA’=A’D∴四边形ACA’D是菱形∵∠ACB=90ο, ∠CAD=30ο∴∠A’CB=60ο又BC=CA=CA’∴△A’BC是等边三角形∴A’B=A’C=A’D∴∠BA’D=60ο-30ο=30ο∴∠DBA’=(180ο-30ο) ÷2=75ο∴∠DBC=15ο同理∠DCB=15ο∴BD=CD△ABC中, ∠A=90ο,AB=AC,BD平分∠ABC,CE⊥BD证明:延长CE交BA延长线于H∵BD平分∠ABC,CE⊥BD∴沿BE对折△BCE与△BHE互相重合∵∠ABD+∠H=90ο∠ACH+∠H=90ο∴∠ABD=∠ACH∵∠BAD=∠HACAB=AC∴△ACH绕点A顺时针旋转90ο与△ABD互相重合 △ABC中,AB=AC, ∠BAC=80ο, ∠PBC=10ο, ∠PCB=30ο,求∠BAP的度数 作∠BAC的平分线与CP延长线交于D,连BD∠BAD=40ο, ∠DPB=40ο △ABD沿AD对折与△ACD重合∠ABD=∠ACD=20ο∠DBP=50ο-20ο-10ο=20ο△ABD沿BD对折与△BPD互相重合AD=DP∠ADC=120ο∠BAP=40ο+30ο=70ο △ABC中,AB>AC,作∠FBC=∠ECB= ∠A,求证:BE=CF1在△MCF内作∠2=∠1△BEM沿BC的中垂线对折互相重合BE=CG∠FGC=∠FBC+∠BCG=∠A+∠2=∠A+∠1∠GFC=∠A+∠1∠GFC=∠FGCCF=CG=BE 三角形ABC中,BC=AC, ∠ACB=90ο,AD=DC,CE⊥BD交BD于E,求证:∠BDC=∠ADF过A作AC的垂线交CF延长线于G △BCD先平移再旋转后与△ACG重合∠BDC=∠AGCAD=DC=AG∠GAF=∠DAF=45ο△AGF沿AF对折与△ADF重合∠BDC=∠AGF=ADF △ABC中, ∠B=60ο, ∠A. ∠C的平分线相交于O,求证:DC+AE=AC∠AOE=∠COD=60ο∠AOC=120ο作∠AOC的平分线OH △AOE沿OA对折与△AOH重合, △COD沿OC对折与△COH重合AE+DC=AH+HC=ACEFADCB 正方形ABCD中,E是AD的中点,求证:AF⊥BE 作正方形的对称轴EG,则沿EG对折△ABE与△DCE互相重合45∠4=∠5连结AC∠3+∠4=∠2+∠5=45ο∠2=∠3沿BD对折△AOF与△COF重合∠1=∠2=∠3∠3+∠BHO=90ο∠1+∠AHE=90οAF⊥BE △ABC是等边三角形,延长BC至D,延长BA至E,使AE=BD,连结CE.DE.求证:CE=DE证明:延长BD到F使DF=BC=AB,连结EF∵BE=AB+AE=BD+DF=BF∴BE=BF, ∠B=60ο,BC=DF∴△EBF为等边三角形∵BF=FE, ∠B=∠F=60ο,BC=DF∴△BCE沿BF边上的高对折能与△EDF重合∴CE=DE 平行四边形ABCD中,BC=2AB,M是AD中点,CE⊥AB,求证:∠DME=3∠AEM 取BC中点N,连结MN,连结CM并延长CM交BA延长线于G四边形MNCD是菱形 CM=MG,EM是直角三角形斜边的中线,EM=MC∠EMN=∠NMC=∠CMD∠DME=3∠EMN=3∠AEM △ABC中,BE、CD是角平分线,P是DE中点,PQ⊥BC,PM⊥AB,PN⊥AC.证:PQ=PM+PNPNMEDCBAQ 三角形ABC中, ∠BAC=120ο,求证:PA+PB+PC>AB+ACPCBA证明:把△APC绕A逆时针旋转60度到△AED位置,连PE∵∠BAC=120ο∴B、A、D三点在一直线上由两点之间线段最短得:PA+PB+PC=PE+BP+ED>AB+AD=AB+AC △ABC中,AD⊥BC, ∠A=45ο,BD=3,DC=2,求△ABC的面积DCBA解:分别以AB.AC为轴做出对称△AFC和△AEB,延长FC.EB交于点G,则四边形AFGE是正方形. 设AD=x则BG=3-x,在直角△BCG中(x-2)2+(x-3)2=(2+3)2解得x=6 △ABC中, ∠C=90ο,BM=AC,点N在AC上,且AN=MC.求证:∠BMP=45οPNMCBA11412113 已知:E.F分别是正方形ABCD的边BC.CD上的点,AE,AF分别与对角线BD交于M、N,若∠EAF=50ο,则∠CME+∠CNF=?∠CNF=∠1+∠3∠CME =∠2+∠4∠CME+∠CNF=∠2+∠4+∠1+∠3=2(∠1+∠2)=100οayxb 正方形被两条与边平行的线段EF.GH分割成四个小矩形,EF与GH交于P,若矩形PFCH的面积恰是矩形AGPE面积的2倍,求∠HAF=?a+b=x+y2ax=bya-x=y-b∴a2-2ax+x2=y2-2by+b2∴(a+x)2=y2+b2=FH2∴BF+DH=FH∴∠FAH=45ο P.Q为△ABC的边AB.AC上的两定点,在BC上取一点R,使△PQR的周长最短。解:作出P关于BC的对称点M,连结MQ,MQ交BC于R,则R就是所求作的点。解:作A关于EF的对称点C,连结BC交EF于点D,则按AD方向撞击黑球,必沿DB反弹击中白球B。 OA.OB表示两条小河,一游客在P点想先到河岸OA观景,再到河岸OB垂钓,最后回到P点,请你替这位游客画出可走的最短路线。P解:1、作点P关于OA.OB的对称点M,N、2.连结MN,MN交OA.OB于D.E两点。3.连结PD,PE、那么游客可走的最短路线是PD、DE、EP。 A.B.C是地面上不在同一直线上的三点,一只青蛙位于地面上的P点,第一步青蛙从P跳到P关于A的对称点P1,第二步青蛙从P跳到P关于A的对称点P2,第三步青蛙从P跳到P关于A的对称点P4…依此跳法类推,问青蛙跳完1999步,落在地面上什么位置上?解:青蛙每跳一次,就完成一个中心对称变换,由中位线定理得:PP2∥2AB∥P3P5, PP2=2AB=P3P5, 并且由P2C=CP3,P6C=CP5,知四边形P3P5P2P6是平行四边形则:P2P6∥P2P, P2P6=P2P 因为1999被6除余1,故青蛙跳完第1999步后,应落在P1位置. BD.CE是三角形ABC的高,点P在BD的延长线上,BP=AC,Q在CE上,CQ=AB,求证(1)AP=AQ,(2)AP⊥AQ12证明:∵ BD.CE是三角形ABC的高∴∠1+∠BAC=90ο, ∠2+∠BAC=90ο∵∠1=∠2∵AB=CQ,BP=AC∴△AQC经平移与旋转后与△ABP互相重合∴AP=AQ, ∠AQC=∠BAC∵∠AQC=∠3+90ο∠BAP=∠3+∠PAQ∴∠3+90ο=∠3+∠PAQ∴∠PAQ=90ο 四边形ABCD中,AC平分∠BAD,并且AB+AD=2AE,求:∠ABC+∠ADC=?DCBA解:作CE⊥AB于E,作CF⊥AD交AD延长线于F∵AC平分∠BAD∴CE=CF,AE=AF=AD+DF∵AB+AD=2AE∴AE+EB+AD=2AE∴AE=AD+EB∴AD+DF=AD+EB∴DF=EB △CBE绕点C旋转后能与△CDF重合22、如图,正三角形ABC边长是1,点O是正三角形ABC的中心,∠MON=1200在∠MON绕着点O旋转过程中
(1)观察∠MON与正三角形ABC围成的四边形POQC的面积是否保持不变? (2)观察CP+CQ的长度是否发生变化? 对于初学者,应先从特殊情况入手。对于图(1),显然四边形POQC 退化为△BOC,面积是正三角形ABC面积的1/3对于图(2),连结OA.OC,则S四边形POQC
=S △QOC + S△POC =S △AOP+ S△POC = S△AOC四边形POQC 面积是正三角形ABC面积的1/3 对于图(3),猜测四边形POQC 面积是正三角形ABC面积的1/3N2、如图,正三角形ABC边长是1,点O是正三角形ABC的中心,∠MON=1200在∠MON绕着点O旋转过程中
(1)观察∠MON与正三角形ABC围成的四边形POQC的面积是否保持不变? (2)观察CP+CQ的长度是否发生变化?解:四边形POQC的面积和CP+CQ的长度都没有发生变化。有已知知:OA=OC∠AOP+ ∠POC=1200∠COQ+ ∠POC=1200∴∠AOP=∠QOC又∠OAP=∠QCO=300∴ △AOP绕O旋转1200后能与△COQ重合∴ S四边形POQC=S △QOC + S△POC =S △AOP+ S△POC = S△AOC四边形POQC 面积是正三角形ABC面积的1/3∴CP+CQ=AP+CP=AC=1旋转的应用 右图正方形KMLN的一个顶点K与正方形ABCD的中心重合,当正方形KMLN绕K运动时,两正方形重叠部分KHBG的面积如何变化? 结论:始终为正方形ABCD面积的四分之一2、如图,正三角形ABC边长是1,点O是正三角形ABC的中心,∠MON=1200在∠MON绕着点O旋转过程中
(1)观察∠MON与正三角形ABC围成的四边形POQC的面积是否保持不变? (2)观察CP+CQ的长度是否发生变化?对于图(2),连结OA.OC,则S四边形POQC
=S △QOC + S△POC =S △AOP+ S△POC = S△AOC四边形POQC 面积是正三角形ABC面积的1/3 对于图(3),猜测四边形POQC 面积是正三角形ABC面积的1/32、如图,正三角形ABC边长是1,点O是正三角形ABC的中心,∠MON=1200在∠MON绕着点O旋转过程中
(1)观察∠MON与正三角形ABC围成的四边形POQC的面积是否保持不变? (2)观察CP+CQ的长度是否发生变化? 对于初学者,应先从特殊情况入手。对于图(1),显然四边形POQC 退化为△BOC,面积是正三角形ABC面积的1/3对于图(2),连结OA.OC,则S四边形POQC
=S △QOC + S△POC =S △AOP+ S△POC = S△AOC四边形POQC 面积是正三角形ABC面积的1/3 对于图(3),猜测四边形POQC 面积是正三角形ABC面积的1/3N 在矩形草地ABCD中,横向阴影部分是矩形道路,另一阴影部分是平行四边形道路。依照图中标注的数据,计算空白部分(长草部分)的面积。ccabccab分析:先将图(1)中的平行四边形M变为图(2)中得矩形N,长草部分的面积不变。再将横向矩形向下平移,这样长草部分的面积就变成了一个长为a-c,宽为b-c的矩形。(1)(2)MN 解:S阴影 =BC ×AB ABDC=(a - c) ×( b - c)=ab – ac – bc + c2 一漆匠用右图所示的胶滚沿从左到右的方向将图案滚涂到墙上,下列给出的四个图案中,符合图示胶滚涂出的图案是( )
