【大单元教学】鲁教版2023年八年级大单元教学7.3二次根式的加减 课件(17张PPT)
文档属性
| 名称 | 【大单元教学】鲁教版2023年八年级大单元教学7.3二次根式的加减 课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 343.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
课时说课
第七章 二次根式
7.3 二次根式的加减
内容及内容解析
1.内容
二次根式加减运算.
2.内容解析
在二次根式性质和乘除运算的基础上,本课进一步学习二次根式的加减运算.二次根式的加减法是把二次根化为最简二次根式后,合并被开方数相同的二次根式就可以了,所以本课内容与整式的加减法类似,在教学中可以让学生体会类比思想的实质,通过具体例子,引导学生探索发现二次根式加减运算的核心是合并被开方数相同的二次根式,基本依据是二次根式的性质和分配律.
基于以上分析,可以确定本课的教学重点是应用分配律进行二次根式的加减运算.
1.目标
(1)掌握二次根式加减运算的步骤和方法.
(2)会灵活运用二次根式的有关性质进行二次根式的加减运算.
2.目标解析
达成目标(1)的标志是学生经历类比合并同类项的方法后能探究归纳,概括出二次根式加减运算的方法,先把每一个二次根式化成最简二次根式,再运用分配律合并被开方数相同的二次根式.
目标(2)是通过例题教学使学生掌握运算的技巧方法,并能在练习中加以运用,能说出依据.
目标和目标解析
教学问题诊断分析
类比思想是根据不同对象在某些方面的类似之处,猜想新、旧知识之间的联系与区别. 在二次根式的加减运算中,最后是合并被开方数相同的二次根式. 但几个二次根式是否可以合并,这一判断没有整式同类项的判断直接. 前者往往需要把每一个二次根式化成最简二次根式,这会造成学生学习的困难. 所以在教学教师引导学生进行类比时,指向一定要明确,由浅入深,总结得出“一化简”、“二判断”、“三合并”的步骤.
本课的教学难点是准确判断可以合并的二次根式,灵活运用性质、算律运算.
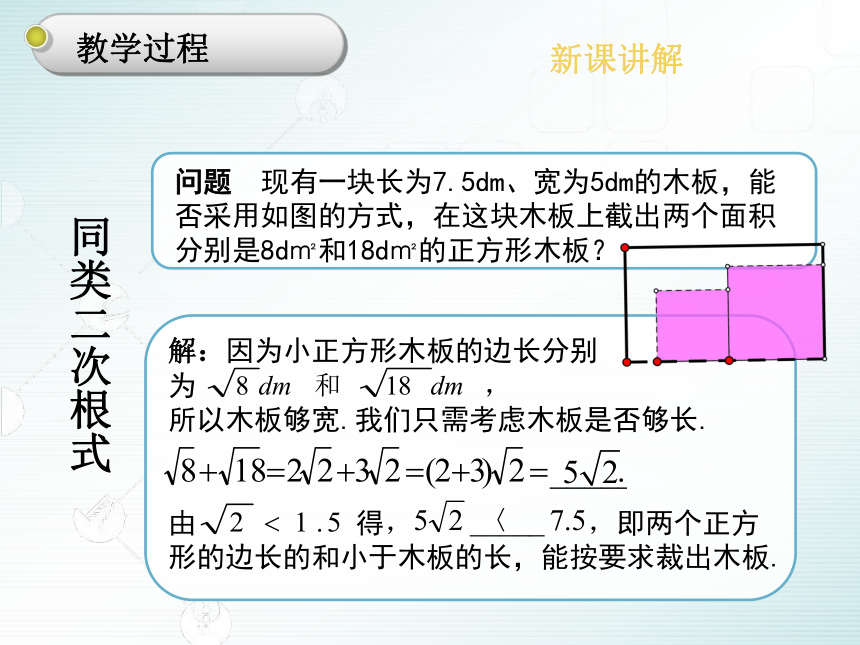
解:因为小正方形木板的边长分别为 ,
所以木板够宽.我们只需考虑木板是否够长.
由 得, ,即两个正方形的边长的和小于木板的长,能按要求裁出木板.
新课讲解
同类二次根式
问题 现有一块长为7.5dm、宽为5dm的木板,能否采用如图的方式,在这块木板上截出两个面积分别是8d㎡和18d㎡的正方形木板?
教学过程
同类二次根式
在这里, 和 化成最简二次根 式 和 后,被开方数_______,像这样的二次根式就叫做同类二次根式.
练一练 下面与 是同类二次根式的是( )
A: B: C: D:
C
相同
二次根式的加减法法则
上面的问题中,利用 律将 和 进行合并.由此得,二次根式的加减法法则:二次根式加减时,可以先将二次根式化成 ,再将 的二次根式进行 .
分配
最简二次根式
被开方数相同
合并
新课讲解
二次根式的加减法法则
例1 计算:
(1) (2)
解:(1)原式= (化成 二次根式)
=( - ) ( 律)
= (合并)
(2)原式= + (化成 二次根式)
=( + ) ( 律)
= (合并)
最简
4
3
分配
最简
分配
3
5
新课讲解
练一练 计算
(1) (2)
二次根式的加减法法则
解:(1)
新课讲解
二次根式的加减法法则
例1 计算:
(1) (2)
解:(1)原式= (化成 二次根式)
=( - ) ( 律)
= (合并)
(2)原式= + (化成 二次根式)
=( + ) ( 律)
= (合并)
最简
4
3
分配
最简
分配
3
5
新课讲解
练一练 计算
(1) (2)
二次根式的加减法法则
解:(1)
新课讲解
知识点二
例2计算 (1)
(2)
解:(1)原式=
= (化简二次根式)
= (合并)
(2)原式= (去括号并化简)
= (合并)
温馨提示:化简后被开方数 的二次根式(同类二次根式)才能合并,因此 合并(填能或不能)
相同
不能
新课讲解
知识点二
练一练
1.下列计算是否正确?为什么?
(1)
(2)
(3)
(4)
错误
错误
正确
错误
新课讲解
2.计算
(1).
解:原式
解:原式
(2)
新课讲解
归纳小结
1、二次根式加减时,可以先将二次根式化成 , 再将 的二次根式进行 .
2、化简后被开方数 的二次根式(同类二
次根式)才能合并,否则不能合并.
3、学习反思
最简二次根式
被开方数相同
合并
相同
强化训练
计算
(1)
解:原式=
解:原式=
(2)
计算
解:原式=
解:原式=
(3)
(4)
强化训练
祝各位老师:
身体健康!万事如意!
课时说课
第七章 二次根式
7.3 二次根式的加减
内容及内容解析
1.内容
二次根式加减运算.
2.内容解析
在二次根式性质和乘除运算的基础上,本课进一步学习二次根式的加减运算.二次根式的加减法是把二次根化为最简二次根式后,合并被开方数相同的二次根式就可以了,所以本课内容与整式的加减法类似,在教学中可以让学生体会类比思想的实质,通过具体例子,引导学生探索发现二次根式加减运算的核心是合并被开方数相同的二次根式,基本依据是二次根式的性质和分配律.
基于以上分析,可以确定本课的教学重点是应用分配律进行二次根式的加减运算.
1.目标
(1)掌握二次根式加减运算的步骤和方法.
(2)会灵活运用二次根式的有关性质进行二次根式的加减运算.
2.目标解析
达成目标(1)的标志是学生经历类比合并同类项的方法后能探究归纳,概括出二次根式加减运算的方法,先把每一个二次根式化成最简二次根式,再运用分配律合并被开方数相同的二次根式.
目标(2)是通过例题教学使学生掌握运算的技巧方法,并能在练习中加以运用,能说出依据.
目标和目标解析
教学问题诊断分析
类比思想是根据不同对象在某些方面的类似之处,猜想新、旧知识之间的联系与区别. 在二次根式的加减运算中,最后是合并被开方数相同的二次根式. 但几个二次根式是否可以合并,这一判断没有整式同类项的判断直接. 前者往往需要把每一个二次根式化成最简二次根式,这会造成学生学习的困难. 所以在教学教师引导学生进行类比时,指向一定要明确,由浅入深,总结得出“一化简”、“二判断”、“三合并”的步骤.
本课的教学难点是准确判断可以合并的二次根式,灵活运用性质、算律运算.
解:因为小正方形木板的边长分别为 ,
所以木板够宽.我们只需考虑木板是否够长.
由 得, ,即两个正方形的边长的和小于木板的长,能按要求裁出木板.
新课讲解
同类二次根式
问题 现有一块长为7.5dm、宽为5dm的木板,能否采用如图的方式,在这块木板上截出两个面积分别是8d㎡和18d㎡的正方形木板?
教学过程
同类二次根式
在这里, 和 化成最简二次根 式 和 后,被开方数_______,像这样的二次根式就叫做同类二次根式.
练一练 下面与 是同类二次根式的是( )
A: B: C: D:
C
相同
二次根式的加减法法则
上面的问题中,利用 律将 和 进行合并.由此得,二次根式的加减法法则:二次根式加减时,可以先将二次根式化成 ,再将 的二次根式进行 .
分配
最简二次根式
被开方数相同
合并
新课讲解
二次根式的加减法法则
例1 计算:
(1) (2)
解:(1)原式= (化成 二次根式)
=( - ) ( 律)
= (合并)
(2)原式= + (化成 二次根式)
=( + ) ( 律)
= (合并)
最简
4
3
分配
最简
分配
3
5
新课讲解
练一练 计算
(1) (2)
二次根式的加减法法则
解:(1)
新课讲解
二次根式的加减法法则
例1 计算:
(1) (2)
解:(1)原式= (化成 二次根式)
=( - ) ( 律)
= (合并)
(2)原式= + (化成 二次根式)
=( + ) ( 律)
= (合并)
最简
4
3
分配
最简
分配
3
5
新课讲解
练一练 计算
(1) (2)
二次根式的加减法法则
解:(1)
新课讲解
知识点二
例2计算 (1)
(2)
解:(1)原式=
= (化简二次根式)
= (合并)
(2)原式= (去括号并化简)
= (合并)
温馨提示:化简后被开方数 的二次根式(同类二次根式)才能合并,因此 合并(填能或不能)
相同
不能
新课讲解
知识点二
练一练
1.下列计算是否正确?为什么?
(1)
(2)
(3)
(4)
错误
错误
正确
错误
新课讲解
2.计算
(1).
解:原式
解:原式
(2)
新课讲解
归纳小结
1、二次根式加减时,可以先将二次根式化成 , 再将 的二次根式进行 .
2、化简后被开方数 的二次根式(同类二
次根式)才能合并,否则不能合并.
3、学习反思
最简二次根式
被开方数相同
合并
相同
强化训练
计算
(1)
解:原式=
解:原式=
(2)
计算
解:原式=
解:原式=
(3)
(4)
强化训练
祝各位老师:
身体健康!万事如意!
