北京市第一七一中学2022-2023学年八年级下学期期中考试数学试卷(PDF版,无答案)
文档属性
| 名称 | 北京市第一七一中学2022-2023学年八年级下学期期中考试数学试卷(PDF版,无答案) |  | |
| 格式 | |||
| 文件大小 | 853.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-01 06:17:46 | ||
图片预览

文档简介
北京市第一七一中学 2022—2023 学年度第二学期
初二年级数学科目 期中调研试题
(时长:100 分钟 总分值:100 分)
一、 选择题(本大题共 10 小题,每小题 3 分,共 30分)
2
1. 计算(√3) 的结果为( ).
A.3 B.3√3 C.6 D.9
2. 下列四组线段中,能.组.成.直角三角形的是( ).
A.6, 7, 8 B.7, 12, 13 C.3, 4, 5 D.5, 9, 12
3. 如图,平行四边形 CD中,∠ = 120°,则∠ 的度数为( ).
A.80° B.60°
C.90° D.120°
4. 下列二次根式中,最简二次根式是( ).
1
A.√3 B.√2.5 C.√ D.√8
2
5. 如图,公路 , 互相垂直,公路 的中点 与点 被湖隔开,若测得 的
长为2.4 ,则 , 两点间距离为( ).
A.0.6 B.1.2 C.1.5 D.2.4
6. 已知点 (2, )在一次函数 = + 1图象上,则 的值为( ).
A.1 B.2 C.3 D.不能确定
7. 某中学组织的全校师生迎“五四”诗词大赛决赛中,25名参赛同学的
得分情况如图所示.这些同学成绩的众数是( ).
A.94 B.96
C.100 D.98
8. 一次投篮训练中,甲、乙、丙、丁四人各进行10次投篮练习,每人投篮成绩的平均数都是9.3,
方差分别为 2甲 = 0.54,
2
乙 = 0.45,
2
丙 = 0.56,
2
丁 = 0.62,成绩最.稳.定.的是( ).
A.甲 B.乙 C.丙 D.丁
第 1 页(共 5 页)
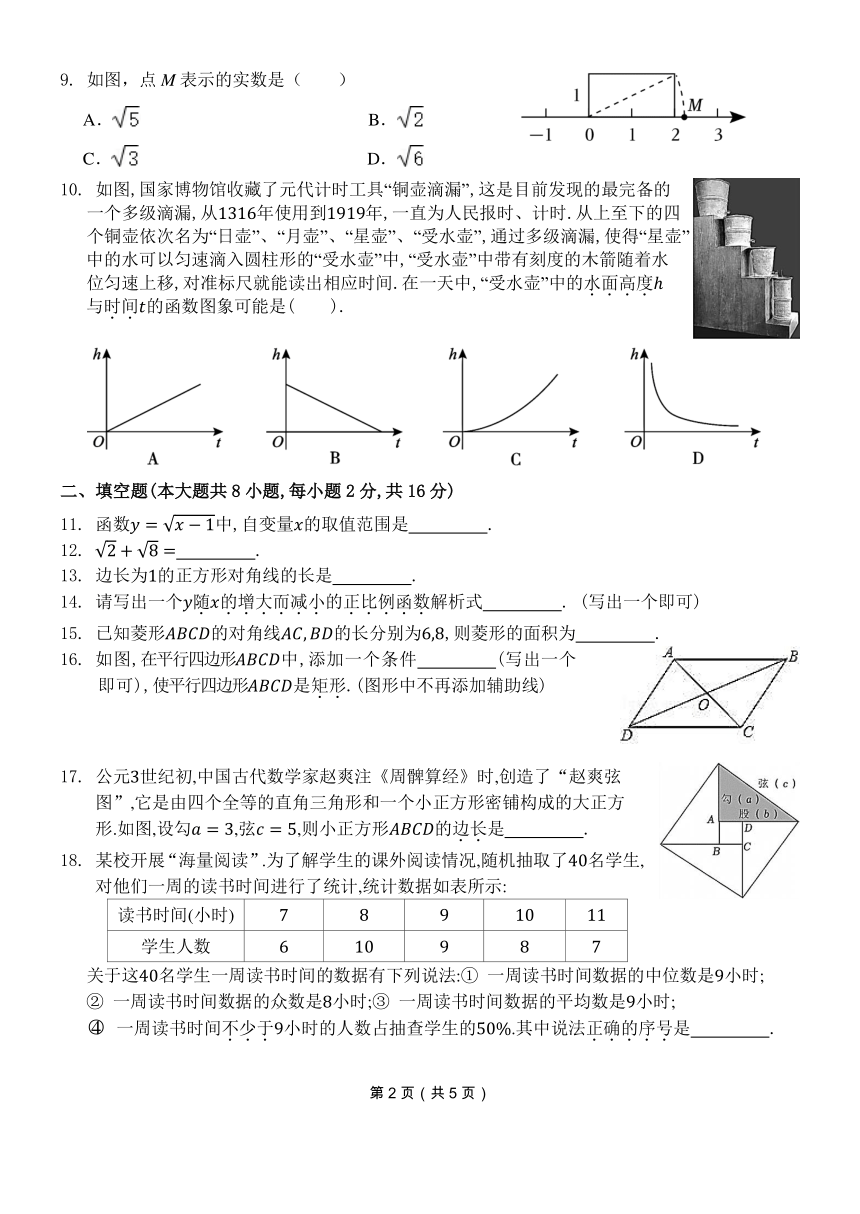
9. 如图,点 M 表示的实数是( )
A. B.
C. D.
10. 如图,国家博物馆收藏了元代计时工具“铜壶滴漏”,这是目前发现的最完备的
一个多级滴漏,从1316年使用到1919年,一直为人民报时、计时.从上至下的四
个铜壶依次名为“日壶”、“月壶”、“星壶”、“受水壶”,通过多级滴漏,使得“星壶”
中的水可以匀速滴入圆柱形的“受水壶”中,“受水壶”中带有刻度的木箭随着水
位匀速上移,对准标尺就能读出相应时间.在一天中,“受水壶”中的水.面.高.度.
与时.间. 的函数图象可能是( ).
二、填空题(本大题共 8 小题,每小题 2分,共 16分)
11. 函数 = √ 1中,自变量 的取值范围是 .
12. √2 + √8 = .
13. 边长为1的正方形对角线的长是 .
14. 请写出一个 随. 的.增.大.而.减.小.的正.比.例.函.数.解析式 . (写出一个即可)
15. 已知菱形 的对角线 , 的长分别为6,8,则菱形的面积为 .
16. 如图,在平行四边形 中,添加一个条件 (写出一个
即可),使平行四边形 是矩.形..(图形中不再添加辅助线)
17. 公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦
图”,它是由四个全等的直角三角形和一个小正方形密铺构成的大正方
形.如图,设勾 = 3,弦 = 5,则小正方形 的边.长.是 .
18. 某校开展“海量阅读”.为了解学生的课外阅读情况,随机抽取了40名学生,
对他们一周的读书时间进行了统计,统计数据如表所示:
读书时间(小时) 7 8 9 10 11
学生人数 6 10 9 8 7
关于这40名学生一周读书时间的数据有下列说法:① 一周读书时间数据的中位数是9小时;
② 一周读书时间数据的众数是8小时;③ 一周读书时间数据的平均数是9小时;
○4 一周读书时间不.少.于.9小时的人数占抽查学生的50%.其中说法正.确.的.序.号.是 .
第 2 页(共 5 页)
二、 解答题(第 19-26题每题 5分,第 27-28题每题 7分,共 54分.解答应写出必要的文字说明,
演算步骤或证明过程)
19.下面是小明设计的“在一个平行四边形内作菱形”的尺规作图过程.
已知:四边形 是平行四边形.
求作:菱形 (点 在 上,点 在 上).
作法:①以点 为圆心, 长为半径作弧,交 于点 ;②以点 为圆心, 长为半径作弧,
交 于点 ;③连接 .所以四边形 为所求的菱形.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保.留.作.图.痕.迹.)
(2)完成下面的证明.
证明: ∵ = , = ,
∴_____ ______.
∵平行四边形 中, ∥ ,即 ∥ ,
∴四边形 为平行四边形.
又∵ = ,
∴四边形 为菱形.(_____________________________)(填推理的依据)
20. 计算:√27 √2 × √8 + √( 2)2.
B
21. 如图,点 、 在□ 的对角线 上,且 = . A E
求证: = .
F
C
D
22. 平面直角坐标系 中,一次函数 = + 1( ≠ 0)的图象经过点 (1,3).
(1)求 的值;
(2)求该一次函数图象与 轴交点坐标;
(3)将这个一次函数图象向.上.平.移.两.个.单.位.后得到的函数解析式是_______________.
23. 如图,在Rt△ 中,∠ = 90°, =12, =13,点 是
Rt△ 外一点,连接 , ,且 =4, =3.
(1)求证:∠ = 90°;
(2)求四边形 面积.
第 3 页(共 5 页)
24. 2023年4月24日是我国第八个“中国航天日”,今年航天日的主题是“格物致知,叩问苍穹”.
设立“中国航天日”,就是要铭记历史、传承精神,激发全民尤其是青少年崇尚科学、探索未知、
敢于创新的热情.某校开展了一次航天知识竞赛(竞赛成绩为百分制),并随机抽取了50名学生
的竞赛成绩,经过收集数据、整理数据,得到以下信息:
a:50名学生竞赛成绩的频数分布直方图如图所示,从左到右依次为第一组到第五组(数据分成
5组:50 ≤ < 60,60 ≤ < 70,70 ≤ < 80,80 ≤ < 90,90 ≤ < 100),
b:第三组的成绩(单位:分)为:71,72,73,73,74,74,75,75,75,78,79,79.
根据以上信息解答下列问题:
(1)补全频数分布直方图(直接在图中补全); 频数(人数)
20
(2)第.三.组.竞赛成绩的众数是_____分,抽.取.的.50名. 18
16
学.生.竞赛成绩的中位数是______分;
14
12
10
(3)若该校共有1000名学生参赛,估计该校参赛学 8
6
生成绩不.低.于.80分的人数. 4
2
0 50 60 70 80 90 100成绩(分)
y
4
25. 如图,平面直角坐标系 中,直线 1: 1 = 2 与 y2= x+a y1=2x3
直线 2: 2 = + 交于点 P(1,m).
2 P
(1)求 , 的值; 1
= 2 –2 –1 O 1 2 3 4
(2)直接写出关于 的二元一次方程组{ 的解; x
= + –1
(3)当 1 < 2时, 的取值范围是_______________.
26. 甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同,均为30元/千克.“五一”假期,两家均
推出了优惠方案,甲采摘园的优惠方案:游客进园需购买60 元的门票,采摘的草莓六折优惠;乙采
摘园的优惠方案:游客进园不需购买门票,采摘的草莓超过一定数量后,超.过.部.分.打.折.优.惠..优惠
期间,设某游客的草莓采摘量为 (千克),在甲采摘园所需总费用为 y 甲(元),在乙采摘园所需总费用
为 y 乙(元),图中折线 表示 y 乙与 x 之间的函数关系.
(1)求 y 甲与 x 之间的函数关系式、y 乙与 x(只求 x≥10 时
直线 )的函数关系式;
(2)当游客采摘15千克的草莓时,你认为他在哪家草莓园
采摘更划算?
第 4 页(共 5 页)
27.如图, 是正方形 的对角线,点 为线段 上一个动点(点 不与点 , 重合),连接 ,
点 在射线 上,且 = .
提出问题:当 运动时,∠ 的度数,线段 , 的数量关系是否发生变化?
探究问题:(1)首先考察点 的一个特殊位置:若∠ = 30°,如图1所示,∠CEF=________,
观察 , 之间的数量关系为________;
(2)考察点 的一般位置:若∠ = ,依.题.意.补.全.图.2,通过观察、测量,发现:
①在一般情况下,∠ =________(用含 的式子表示);
②判.断.并.证.明.线段 , 的数量关系.
28.在平面直角坐标系 中,对于两点 , 给出如下定义:以线段 为边的正方形称为点 , 的
“确定正方形”.如图 1 为点 , 的“确定正方形”的示意图.
y y
6 6
5 D 5C
4
4
3
3 2
2 1
1 A B –7 –6 –5 –4 –3 –2 –1 O 1 2 3 4 5 6 x
–1
–7 –6 –5 –4 –3 –2 –1 O 1 2 3 4 5 6 7 x –2
–1
图1 –3 备用图
–2 –4
–3
(1)如果–4点 的坐标为(0,1),点 的坐标为(3,1),那么点 , 的“确定正方形”的面积为____;
(2)已知点 的坐标为(0,0),点 为直线 = + 上一动点,当点 , 的“确定正方形”的面积最小,
且最小面积为2时,求 的值.
(3)已知点 在以边长为2的正方形的边上,且该正方形的边与两坐标轴平行,对角线交点为 ( , 0),
点 在直线 = 2上,若要使所有点 , 的“确定正方形”的面积都不小于2,直接写出 的
取值范围.
第 5 页(共 5 页)
初二年级数学科目 期中调研试题
(时长:100 分钟 总分值:100 分)
一、 选择题(本大题共 10 小题,每小题 3 分,共 30分)
2
1. 计算(√3) 的结果为( ).
A.3 B.3√3 C.6 D.9
2. 下列四组线段中,能.组.成.直角三角形的是( ).
A.6, 7, 8 B.7, 12, 13 C.3, 4, 5 D.5, 9, 12
3. 如图,平行四边形 CD中,∠ = 120°,则∠ 的度数为( ).
A.80° B.60°
C.90° D.120°
4. 下列二次根式中,最简二次根式是( ).
1
A.√3 B.√2.5 C.√ D.√8
2
5. 如图,公路 , 互相垂直,公路 的中点 与点 被湖隔开,若测得 的
长为2.4 ,则 , 两点间距离为( ).
A.0.6 B.1.2 C.1.5 D.2.4
6. 已知点 (2, )在一次函数 = + 1图象上,则 的值为( ).
A.1 B.2 C.3 D.不能确定
7. 某中学组织的全校师生迎“五四”诗词大赛决赛中,25名参赛同学的
得分情况如图所示.这些同学成绩的众数是( ).
A.94 B.96
C.100 D.98
8. 一次投篮训练中,甲、乙、丙、丁四人各进行10次投篮练习,每人投篮成绩的平均数都是9.3,
方差分别为 2甲 = 0.54,
2
乙 = 0.45,
2
丙 = 0.56,
2
丁 = 0.62,成绩最.稳.定.的是( ).
A.甲 B.乙 C.丙 D.丁
第 1 页(共 5 页)
9. 如图,点 M 表示的实数是( )
A. B.
C. D.
10. 如图,国家博物馆收藏了元代计时工具“铜壶滴漏”,这是目前发现的最完备的
一个多级滴漏,从1316年使用到1919年,一直为人民报时、计时.从上至下的四
个铜壶依次名为“日壶”、“月壶”、“星壶”、“受水壶”,通过多级滴漏,使得“星壶”
中的水可以匀速滴入圆柱形的“受水壶”中,“受水壶”中带有刻度的木箭随着水
位匀速上移,对准标尺就能读出相应时间.在一天中,“受水壶”中的水.面.高.度.
与时.间. 的函数图象可能是( ).
二、填空题(本大题共 8 小题,每小题 2分,共 16分)
11. 函数 = √ 1中,自变量 的取值范围是 .
12. √2 + √8 = .
13. 边长为1的正方形对角线的长是 .
14. 请写出一个 随. 的.增.大.而.减.小.的正.比.例.函.数.解析式 . (写出一个即可)
15. 已知菱形 的对角线 , 的长分别为6,8,则菱形的面积为 .
16. 如图,在平行四边形 中,添加一个条件 (写出一个
即可),使平行四边形 是矩.形..(图形中不再添加辅助线)
17. 公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦
图”,它是由四个全等的直角三角形和一个小正方形密铺构成的大正方
形.如图,设勾 = 3,弦 = 5,则小正方形 的边.长.是 .
18. 某校开展“海量阅读”.为了解学生的课外阅读情况,随机抽取了40名学生,
对他们一周的读书时间进行了统计,统计数据如表所示:
读书时间(小时) 7 8 9 10 11
学生人数 6 10 9 8 7
关于这40名学生一周读书时间的数据有下列说法:① 一周读书时间数据的中位数是9小时;
② 一周读书时间数据的众数是8小时;③ 一周读书时间数据的平均数是9小时;
○4 一周读书时间不.少.于.9小时的人数占抽查学生的50%.其中说法正.确.的.序.号.是 .
第 2 页(共 5 页)
二、 解答题(第 19-26题每题 5分,第 27-28题每题 7分,共 54分.解答应写出必要的文字说明,
演算步骤或证明过程)
19.下面是小明设计的“在一个平行四边形内作菱形”的尺规作图过程.
已知:四边形 是平行四边形.
求作:菱形 (点 在 上,点 在 上).
作法:①以点 为圆心, 长为半径作弧,交 于点 ;②以点 为圆心, 长为半径作弧,
交 于点 ;③连接 .所以四边形 为所求的菱形.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保.留.作.图.痕.迹.)
(2)完成下面的证明.
证明: ∵ = , = ,
∴_____ ______.
∵平行四边形 中, ∥ ,即 ∥ ,
∴四边形 为平行四边形.
又∵ = ,
∴四边形 为菱形.(_____________________________)(填推理的依据)
20. 计算:√27 √2 × √8 + √( 2)2.
B
21. 如图,点 、 在□ 的对角线 上,且 = . A E
求证: = .
F
C
D
22. 平面直角坐标系 中,一次函数 = + 1( ≠ 0)的图象经过点 (1,3).
(1)求 的值;
(2)求该一次函数图象与 轴交点坐标;
(3)将这个一次函数图象向.上.平.移.两.个.单.位.后得到的函数解析式是_______________.
23. 如图,在Rt△ 中,∠ = 90°, =12, =13,点 是
Rt△ 外一点,连接 , ,且 =4, =3.
(1)求证:∠ = 90°;
(2)求四边形 面积.
第 3 页(共 5 页)
24. 2023年4月24日是我国第八个“中国航天日”,今年航天日的主题是“格物致知,叩问苍穹”.
设立“中国航天日”,就是要铭记历史、传承精神,激发全民尤其是青少年崇尚科学、探索未知、
敢于创新的热情.某校开展了一次航天知识竞赛(竞赛成绩为百分制),并随机抽取了50名学生
的竞赛成绩,经过收集数据、整理数据,得到以下信息:
a:50名学生竞赛成绩的频数分布直方图如图所示,从左到右依次为第一组到第五组(数据分成
5组:50 ≤ < 60,60 ≤ < 70,70 ≤ < 80,80 ≤ < 90,90 ≤ < 100),
b:第三组的成绩(单位:分)为:71,72,73,73,74,74,75,75,75,78,79,79.
根据以上信息解答下列问题:
(1)补全频数分布直方图(直接在图中补全); 频数(人数)
20
(2)第.三.组.竞赛成绩的众数是_____分,抽.取.的.50名. 18
16
学.生.竞赛成绩的中位数是______分;
14
12
10
(3)若该校共有1000名学生参赛,估计该校参赛学 8
6
生成绩不.低.于.80分的人数. 4
2
0 50 60 70 80 90 100成绩(分)
y
4
25. 如图,平面直角坐标系 中,直线 1: 1 = 2 与 y2= x+a y1=2x3
直线 2: 2 = + 交于点 P(1,m).
2 P
(1)求 , 的值; 1
= 2 –2 –1 O 1 2 3 4
(2)直接写出关于 的二元一次方程组{ 的解; x
= + –1
(3)当 1 < 2时, 的取值范围是_______________.
26. 甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同,均为30元/千克.“五一”假期,两家均
推出了优惠方案,甲采摘园的优惠方案:游客进园需购买60 元的门票,采摘的草莓六折优惠;乙采
摘园的优惠方案:游客进园不需购买门票,采摘的草莓超过一定数量后,超.过.部.分.打.折.优.惠..优惠
期间,设某游客的草莓采摘量为 (千克),在甲采摘园所需总费用为 y 甲(元),在乙采摘园所需总费用
为 y 乙(元),图中折线 表示 y 乙与 x 之间的函数关系.
(1)求 y 甲与 x 之间的函数关系式、y 乙与 x(只求 x≥10 时
直线 )的函数关系式;
(2)当游客采摘15千克的草莓时,你认为他在哪家草莓园
采摘更划算?
第 4 页(共 5 页)
27.如图, 是正方形 的对角线,点 为线段 上一个动点(点 不与点 , 重合),连接 ,
点 在射线 上,且 = .
提出问题:当 运动时,∠ 的度数,线段 , 的数量关系是否发生变化?
探究问题:(1)首先考察点 的一个特殊位置:若∠ = 30°,如图1所示,∠CEF=________,
观察 , 之间的数量关系为________;
(2)考察点 的一般位置:若∠ = ,依.题.意.补.全.图.2,通过观察、测量,发现:
①在一般情况下,∠ =________(用含 的式子表示);
②判.断.并.证.明.线段 , 的数量关系.
28.在平面直角坐标系 中,对于两点 , 给出如下定义:以线段 为边的正方形称为点 , 的
“确定正方形”.如图 1 为点 , 的“确定正方形”的示意图.
y y
6 6
5 D 5C
4
4
3
3 2
2 1
1 A B –7 –6 –5 –4 –3 –2 –1 O 1 2 3 4 5 6 x
–1
–7 –6 –5 –4 –3 –2 –1 O 1 2 3 4 5 6 7 x –2
–1
图1 –3 备用图
–2 –4
–3
(1)如果–4点 的坐标为(0,1),点 的坐标为(3,1),那么点 , 的“确定正方形”的面积为____;
(2)已知点 的坐标为(0,0),点 为直线 = + 上一动点,当点 , 的“确定正方形”的面积最小,
且最小面积为2时,求 的值.
(3)已知点 在以边长为2的正方形的边上,且该正方形的边与两坐标轴平行,对角线交点为 ( , 0),
点 在直线 = 2上,若要使所有点 , 的“确定正方形”的面积都不小于2,直接写出 的
取值范围.
第 5 页(共 5 页)
同课章节目录
