人教八年级下册 19.1.1变量与函数课后巩固练习(含答案)
文档属性
| 名称 | 人教八年级下册 19.1.1变量与函数课后巩固练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 177.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-01 08:38:47 | ||
图片预览


文档简介
19.1.1 变量与函数 课后巩固练习
一、单选题
1.下列选项中哪个函数与函数y=x是相同的函数是( )
A.y= B.y= C.y= D.选项A、B、C都是
2.在圆周长计算公式C=2πr中,变量有( )
A.C,π B.C,r C.C,π,r D.2π,r
3.函数的自变量取值范围是( )
A. B. C. D.且
4.下列式子:①;②;③;④.其中是的函数的个数是( )
A.1 B.2 C.3 D.4
5.已知声音在空气中的传播速度与空气的温度有关,在一定范围内,其关系如表所示:
温度℃ ﹣20 ﹣10 0 10 20 30
传播速度/(m/s) 319 325 331 337 343 349
下列说法错误的是( )
A.自变量是温度,因变量是传播速度
B.温度越高,传播速度越快
C.当温度为10℃时,声音5s可以传播1655m
D.温度每升高10℃,传播速度增加6m/s
6.函数中,自变量x的取值范围是( )
A.x≥-1 B.x>-1 C.x≥1 D.x>-1
7.某品牌热水壶的成本为50元,销售商对其销量与定价的关系进行了调查,结果如下:
定价/元 70 80 90 100 110 120
销量/把 80 100 110 100 80 60
现销售了把水壶,则定价约为( )
A.元 B.元 C.元 D.元
8.函数的自变量的取值范围是( )
A. B.且 C.且 D.且
9.下列函数中,自变量x可以取1和2的函数是( )
A.y= B.y= C.y= D.y=
10.下列语句中,与是一次函数关系的有( )个.
(1)汽车以80千米/时的速度匀速行驶,行驶路程(千米)与行驶时间(时)之间的关系;
(2)圆的面积(厘米)与它的半径(厘米)之间的关系;
(3)一棵树现在高50厘米,每个月平均长高2厘米,月后这棵树的高度是厘米,与的关系;
(4)猪肉的单价是60元/千克,当购买千克猪肉时,花费元,与的关系.
A.1 B.2 C.3 D.4
二、填空题
11.某人购进一批苹果,到市场零售,已知销售额y(元)与卖出的苹果数量x(千克)的关系如表所示:则y与x之间的关系式为__________.
数量x(千克) 2 3 4 5 …
销售额y(元) 7.2 10.8 14.4 18.0 …
12.已知f(x)=2,那么f(-1)=_______.
13.某商店进了一批货,每件3元,出售时每件加价0.5元,如售出x件应收入货款y元,那么y(元)与x(件)的函数表达式是_________________.
14.圆柱的高是10 cm,圆柱底面圆的半径为r cm,圆柱的侧面展开图的面积Scm2.圆柱侧面展开图的面积s与圆柱底面半径r之间的关系式是___.
15.函数y=中自变量x的取值范围是________,若x=4,则函数值y=________.
三、解答题
16.已知一个长方形的长是,宽是,周长是,面积是.
(1)长方形的周长与长之间的关系式是什么?
(2)长方形的面积与长之间的关系式是什么?
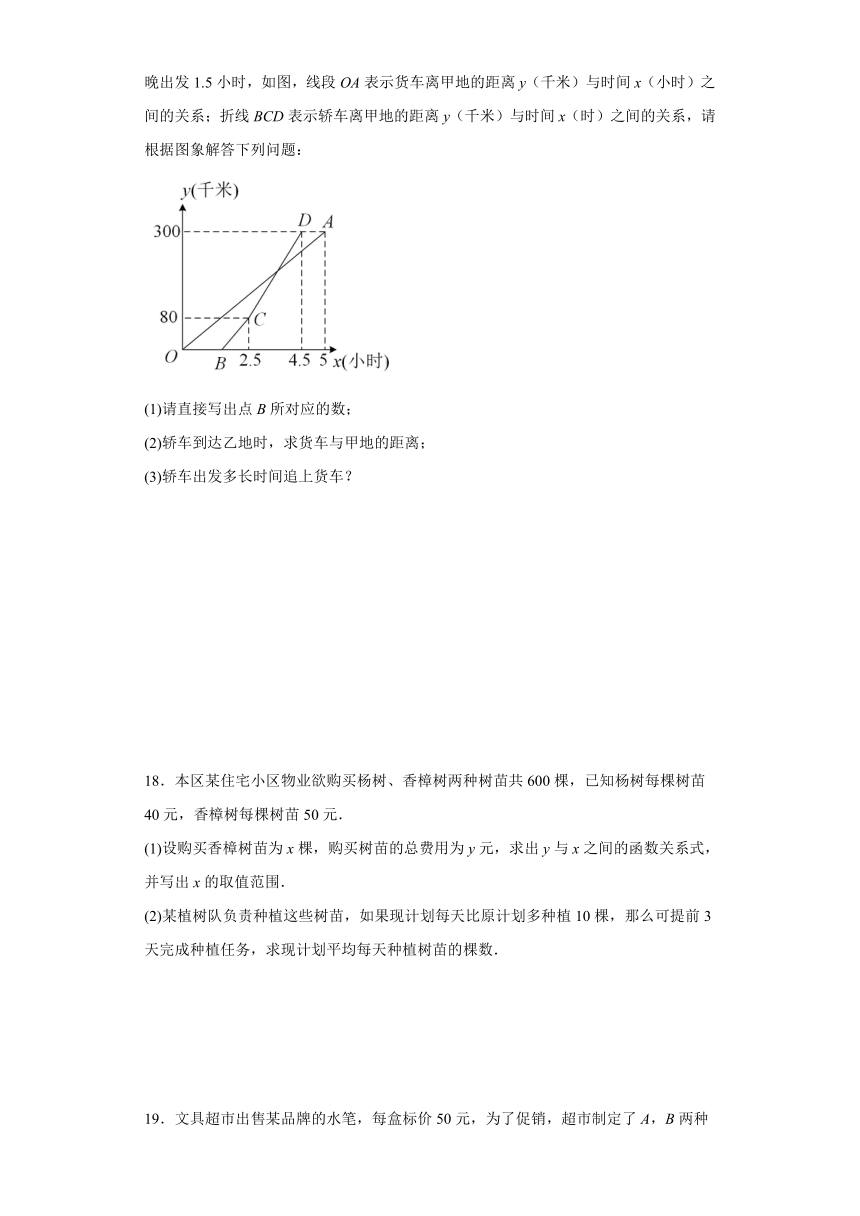
17.甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的关系,请根据图象解答下列问题:
(1)请直接写出点B所对应的数;
(2)轿车到达乙地时,求货车与甲地的距离;
(3)轿车出发多长时间追上货车?
18.本区某住宅小区物业欲购买杨树、香樟树两种树苗共600棵,已知杨树每棵树苗40元,香樟树每棵树苗50元.
(1)设购买香樟树苗为x棵,购买树苗的总费用为y元,求出y与x之间的函数关系式,并写出x的取值范围.
(2)某植树队负责种植这些树苗,如果现计划每天比原计划多种植10棵,那么可提前3天完成种植任务,求现计划平均每天种植树苗的棵数.
19.文具超市出售某品牌的水笔,每盒标价50元,为了促销,超市制定了A,B两种方案:A:每盒水笔打九折;B:5盒以内(包括5盒)不打折,超过5盒后,超过的部分打8折.
(1)若购买水笔x盒,请分别直接写出用A方案购买水笔的费用(元)和用B方案购买水笔的费用(元)关于x(盒)的关系式;
(2)若你去购买水笔,如何选择哪种方案更优惠?请说明理由.
20.观察下列一组图形,其中图①中共有2颗星,图②中共有6颗星,图③中共有11颗星,图④中共有17颗星……按此规律.
(1)图⑧中星星的颗数是_______;
(2)设图 中星星的个数为S,试写出S与n的关系式;
(3)指出上述变化过程中,变量、常量分别是什么?
参考答案
1.C
2.B
3.D
4.C
5.C
6.A
7.C
8.C
9.D
10.C
11.y=3.6x
12.2
13.y=3.5x
14.s=20πr
15. x≥3 y=1
16.(1)解:,即
(2)解:
17.(1)解:∵轿车比货车晚出发1.5小时,货车是第0小时除法,
∴轿车第1.5小时出发,
∴点B所对应的数是1.5;
(2)解:根据图象可知,货车速度是(千米/小时),
(千米),
∴轿车到达乙地时,货车与甲地的距离是270千米;
(3)解:∵轿车在CD段的速度是:(千米/小时),
设轿车出发x小时追上货车,
∴,
解得,
∴轿车出发2.4小时追上货车.
18.(1)解:由题意可得,,
即y与x之间的函数关系式是:.
(2)解:设现计划平均每天种植树苗a棵,
由题意得:,
解得,a=50或a=-40(舍去),
检验:当a=50时,,
故原分式方程的解是a=50,
答:现计划平均每天种植50棵.
19. (1)解:
(2)解:①当的整数时,∵,,
∴∴选择A方案更优惠;
②当的整数时∵,,
∴分三种情况
(i)当时,即
∴,
(ii)当时,即
∴,
(iii)当时,即
∴.
综上所述,当购买10盒时,A、B两种方案一样的优惠 ;当购买小于10盒时,A方案更优惠;当购买大于10盒时,B方案更优惠.
20. (1) 51
相邻两数之间的差越来越大,以此规律可以推出图⑧的星星数量.
(2)S=1+2+…+n+(2n-1)=+2n-1=n2+n-1
(3)变量是n和S,常量是,,-1
一、单选题
1.下列选项中哪个函数与函数y=x是相同的函数是( )
A.y= B.y= C.y= D.选项A、B、C都是
2.在圆周长计算公式C=2πr中,变量有( )
A.C,π B.C,r C.C,π,r D.2π,r
3.函数的自变量取值范围是( )
A. B. C. D.且
4.下列式子:①;②;③;④.其中是的函数的个数是( )
A.1 B.2 C.3 D.4
5.已知声音在空气中的传播速度与空气的温度有关,在一定范围内,其关系如表所示:
温度℃ ﹣20 ﹣10 0 10 20 30
传播速度/(m/s) 319 325 331 337 343 349
下列说法错误的是( )
A.自变量是温度,因变量是传播速度
B.温度越高,传播速度越快
C.当温度为10℃时,声音5s可以传播1655m
D.温度每升高10℃,传播速度增加6m/s
6.函数中,自变量x的取值范围是( )
A.x≥-1 B.x>-1 C.x≥1 D.x>-1
7.某品牌热水壶的成本为50元,销售商对其销量与定价的关系进行了调查,结果如下:
定价/元 70 80 90 100 110 120
销量/把 80 100 110 100 80 60
现销售了把水壶,则定价约为( )
A.元 B.元 C.元 D.元
8.函数的自变量的取值范围是( )
A. B.且 C.且 D.且
9.下列函数中,自变量x可以取1和2的函数是( )
A.y= B.y= C.y= D.y=
10.下列语句中,与是一次函数关系的有( )个.
(1)汽车以80千米/时的速度匀速行驶,行驶路程(千米)与行驶时间(时)之间的关系;
(2)圆的面积(厘米)与它的半径(厘米)之间的关系;
(3)一棵树现在高50厘米,每个月平均长高2厘米,月后这棵树的高度是厘米,与的关系;
(4)猪肉的单价是60元/千克,当购买千克猪肉时,花费元,与的关系.
A.1 B.2 C.3 D.4
二、填空题
11.某人购进一批苹果,到市场零售,已知销售额y(元)与卖出的苹果数量x(千克)的关系如表所示:则y与x之间的关系式为__________.
数量x(千克) 2 3 4 5 …
销售额y(元) 7.2 10.8 14.4 18.0 …
12.已知f(x)=2,那么f(-1)=_______.
13.某商店进了一批货,每件3元,出售时每件加价0.5元,如售出x件应收入货款y元,那么y(元)与x(件)的函数表达式是_________________.
14.圆柱的高是10 cm,圆柱底面圆的半径为r cm,圆柱的侧面展开图的面积Scm2.圆柱侧面展开图的面积s与圆柱底面半径r之间的关系式是___.
15.函数y=中自变量x的取值范围是________,若x=4,则函数值y=________.
三、解答题
16.已知一个长方形的长是,宽是,周长是,面积是.
(1)长方形的周长与长之间的关系式是什么?
(2)长方形的面积与长之间的关系式是什么?
17.甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段OA表示货车离甲地的距离y(千米)与时间x(小时)之间的关系;折线BCD表示轿车离甲地的距离y(千米)与时间x(时)之间的关系,请根据图象解答下列问题:
(1)请直接写出点B所对应的数;
(2)轿车到达乙地时,求货车与甲地的距离;
(3)轿车出发多长时间追上货车?
18.本区某住宅小区物业欲购买杨树、香樟树两种树苗共600棵,已知杨树每棵树苗40元,香樟树每棵树苗50元.
(1)设购买香樟树苗为x棵,购买树苗的总费用为y元,求出y与x之间的函数关系式,并写出x的取值范围.
(2)某植树队负责种植这些树苗,如果现计划每天比原计划多种植10棵,那么可提前3天完成种植任务,求现计划平均每天种植树苗的棵数.
19.文具超市出售某品牌的水笔,每盒标价50元,为了促销,超市制定了A,B两种方案:A:每盒水笔打九折;B:5盒以内(包括5盒)不打折,超过5盒后,超过的部分打8折.
(1)若购买水笔x盒,请分别直接写出用A方案购买水笔的费用(元)和用B方案购买水笔的费用(元)关于x(盒)的关系式;
(2)若你去购买水笔,如何选择哪种方案更优惠?请说明理由.
20.观察下列一组图形,其中图①中共有2颗星,图②中共有6颗星,图③中共有11颗星,图④中共有17颗星……按此规律.
(1)图⑧中星星的颗数是_______;
(2)设图 中星星的个数为S,试写出S与n的关系式;
(3)指出上述变化过程中,变量、常量分别是什么?
参考答案
1.C
2.B
3.D
4.C
5.C
6.A
7.C
8.C
9.D
10.C
11.y=3.6x
12.2
13.y=3.5x
14.s=20πr
15. x≥3 y=1
16.(1)解:,即
(2)解:
17.(1)解:∵轿车比货车晚出发1.5小时,货车是第0小时除法,
∴轿车第1.5小时出发,
∴点B所对应的数是1.5;
(2)解:根据图象可知,货车速度是(千米/小时),
(千米),
∴轿车到达乙地时,货车与甲地的距离是270千米;
(3)解:∵轿车在CD段的速度是:(千米/小时),
设轿车出发x小时追上货车,
∴,
解得,
∴轿车出发2.4小时追上货车.
18.(1)解:由题意可得,,
即y与x之间的函数关系式是:.
(2)解:设现计划平均每天种植树苗a棵,
由题意得:,
解得,a=50或a=-40(舍去),
检验:当a=50时,,
故原分式方程的解是a=50,
答:现计划平均每天种植50棵.
19. (1)解:
(2)解:①当的整数时,∵,,
∴∴选择A方案更优惠;
②当的整数时∵,,
∴分三种情况
(i)当时,即
∴,
(ii)当时,即
∴,
(iii)当时,即
∴.
综上所述,当购买10盒时,A、B两种方案一样的优惠 ;当购买小于10盒时,A方案更优惠;当购买大于10盒时,B方案更优惠.
20. (1) 51
相邻两数之间的差越来越大,以此规律可以推出图⑧的星星数量.
(2)S=1+2+…+n+(2n-1)=+2n-1=n2+n-1
(3)变量是n和S,常量是,,-1
