第四章 《图形的平移与旋转》复习与巩固学案
文档属性
| 名称 | 第四章 《图形的平移与旋转》复习与巩固学案 |  | |
| 格式 | docx | ||
| 文件大小 | 553.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-28 15:03:14 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
《图形的平移与旋转》复习与巩固
【学习目标】
1.了解平移、旋转、中心对称,探索它们的基本性质;
2.能够按要求作出简单平面图形经过平移、旋转后的图形,能作出简单平面图形经过一次或两次图形变换后的图形;
3.利用平移、旋转、中心对称、轴对称及其组合进行图案设计,认识和欣赏轴对称、平移、旋转在现实生活中的应用.
【课前梳理】
1. 平移的概念:在平面内,将一个图形 移动一定的距离,这样的图形运动称为平移,平移不改变图形的 和 .
2.平移的基本性质:一个图形和它经过平移所得的图形中,对应点所连的线段 (或 )且 ;对应线段 (或 )且 ;,对应角 .
3. 点的平移引起坐标的变化规律:沿x轴正方向平移,则 坐标加上平移单位的数量,沿x轴负方向平移,则 坐标减去平移单位的数量;沿y轴正方向平移,则 坐标加上平移的单位数量,沿y轴负方向平移,则 坐标减去平移单位的数量.即:“上加下减,左减右加”
4.旋转概念:在 内,将一个图形绕一个 按某个方向转动一个角度,这样的图形运动称为旋转.这个定点称为 ,转动的角称为 .
5.旋转变换的性质:一个图形和它经过旋转所得的图形中,对应点到旋转中心的距离 ,任意一组对应点与旋转中心的连线所成的角都等于 ;对应线段 ,对应角 .
6.旋转三要素: 、 、 .
7.中心对称概念:把一个图形绕着某一点旋转 ,它能够与另一个图形重合,那么就说这两个图形关于这个点成 ,这个点叫做它们的 .
8.中心对称的性质:成中心对称的两个图形中,对应点所连线段经过 ,且被对称中心 .
9.中心对称图形:把一个图形绕着某点旋转 ,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做 ,这个点叫做它的 .
10.平移、旋转、中心对称三种变换的关系:图形经过平移、旋转或中心对称的变换后,虽然对应位置改变了,但 和 没有改变,即两个图形是全等的.
【课堂练习】
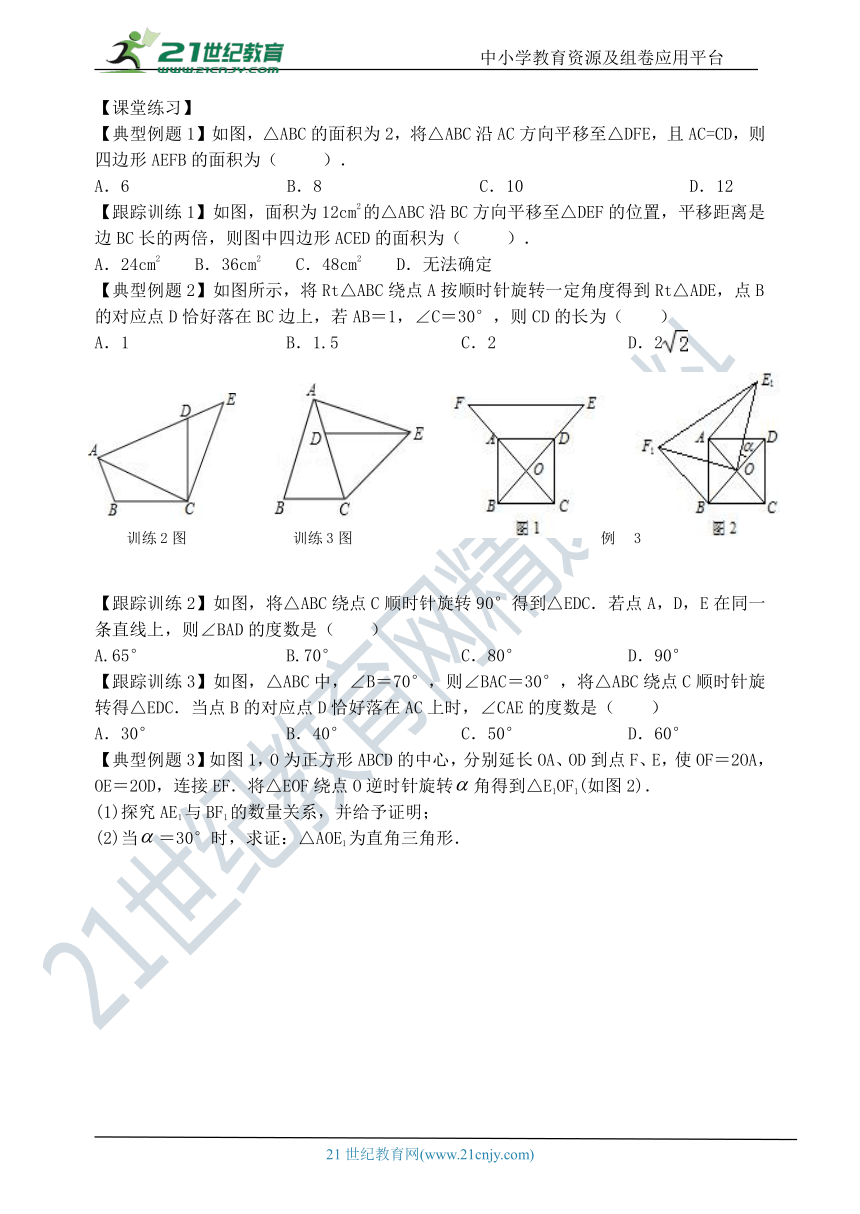
【典型例题1】如图,△ABC的面积为2,将△ABC沿AC方向平移至△DFE,且AC=CD,则四边形AEFB的面积为( ).
A.6 B.8 C.10 D.12
【跟踪训练1】如图,面积为12cm2的△ABC沿BC方向平移至△DEF的位置,平移距离是边BC长的两倍,则图中四边形ACED的面积为( ).
A.24cm2 B.36cm2 C.48cm2 D.无法确定
【典型例题2】如图所示,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠C=30°,则CD的长为( )
A.1 B.1.5 C.2 D.2
【跟踪训练2】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,则∠BAD的度数是( )
A.65° B.70° C.80° D.90°
【跟踪训练3】如图,△ABC中,∠B=70°,则∠BAC=30°,将△ABC绕点C顺时针旋转得△EDC.当点B的对应点D恰好落在AC上时,∠CAE的度数是( )
A.30° B.40° C.50° D.60°
【典型例题3】如图1,O为正方形ABCD的中心,分别延长OA、OD到点F、E,使OF=2OA,OE=2OD,连接EF.将△EOF绕点O逆时针旋转角得到△E1OF1(如图2).
(1)探究AE1与BF1的数量关系,并给予证明;
(2)当=30°时,求证:△AOE1为直角三角形.
【跟踪训练4】在等边三角形ABC中有一点P,已知PC=2, PA=4,PB=,则∠APB= .
【巩固训练】
1.下列运动属于平移的是( )
A.转动的电风扇的叶片
B.打气筒打气时活塞的运动
C.行驶的自行车的后轮
D.在游乐场荡秋千的小朋友
2.把下列数字看成图形,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.在平面直角坐标系中,将点向右平移4个单位长度后得到的点的坐标为
A.(2,3) B.(-6,3) C.(-2,7) D.(-2,-1)
4.如图图形中,把△ABC平移后能得到△DEF的是( )
5.如图,三角形ABC沿着由点B到点E的方向平移到三角形DEF的位置,已知BC=8,EC=5,那么平移的距离为( )
A.13 B.8 C.5 D.3
6.如图,三角形ABC经过平移后得到三角形DEF,下列说法:①AB∥DE;②AD=BE;③∠ACB=∠DFE;④BC=DE.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是AC的中点,将CD绕着点C逆时针旋转一周,在旋转的过程中,点D的对应点为点E,连接AE、BE,则△AEB面积的最小值是( )
A.1 B.2 C.3 D.4
二、填空题
8.如图,将△ABC沿BC方向平移2cm得到△DEF.如果四边形ABFD的周长是20cm,则△ABC周长
是 cm.
9.已知点M(1﹣2m,m﹣1)关于原点的对称点在第一象限,则m的取值范围是 .
10.如图,O是边长为6的等边△ABC三边中垂线的交点,将△ABC绕点O逆时针方向旋转180°,得到△A1B1C1,则图中阴影部分的面积为 .
11.如图,在直角坐标系中,将△AOB绕原点旋转到△OCD,其中A(-3,-1),B(4,3),点D在轴正半轴上,则点C的坐标为 .
12.如图,把△ABC绕点C顺时针旋转得到△A'B'C',此时A′B′⊥AC于D,已知∠A=50°,则∠B′CB的度数是 °.
三、解答题
13.已知,△ABC三个顶点的坐标分别为:A(﹣3,﹣2)、B(﹣5,0)、C(﹣2,2).
(1)在平面直角坐标系中画出△ABC;
(2)将△ABC向右平移5个单位长度,再向上移2个单位长度,画出平移后的△A1B1C1;
(3)计算△A1B1C1的面积.
14.如图,矩形ABCD与矩形A’B’C’D’关于点A 成中心对称,试判定四边形BDB’D’的形状,并说明你的理由
15.已知△ABC是等边三角形,D是∠ABC外-点,且∠BDC=120°,求证:BD+CD=AD.
16.(1)如图①,已知正方形ABCD,点E,F分别在边BC,AB上,且BE=BF.此时AF与CE有怎样的数量关系?
(2)如图②,△BEF绕点B顺时针旋转∠α.当0°<α<90°时,连接AF,CE,此时AF与CE仍有(1)中的数量关系吗?如果成立,请说明理由.否则,请举出反例;
(3)当α=90°时(图③),连接AF,CE.猜想AB与BE有什么数量关系时,直线AF是EC的垂直平行线?试说明理由.
《图形的平移与旋转》章节复习
课堂练习
典型例题1.C 跟踪训练1.36 典型例题2.1 跟踪训练2.D 跟踪训练3.C
典型例题3. (1)AE1=BF1.
证明:∵O为正方形ABCD的中心,∴OA=OD,
∵OF=2OA,OE=2OD,
∴OE=OF,
∵将△EOF绕点O逆时针旋转α角得到△E1OF1
∴OE1=OF1,
∵∠F1OB=∠E1OA,OA=OB,
∴△E1AO≌△F1BO,∴AE1=BF1;
(2)证明:∵取OE1中点G,连接AG,
∵∠AOD=90 ,α=30 ,
∴∠E1OA=90 -α=60 ,
∵OE1=2OA,∴OA=OG,
∴∠E1OA=∠AGO=∠OAG=60 ,
∴AG=GE1,
∴∠GAE1=∠GE1A=30 ,
∴∠E1AO=90 ,
∴△AOE1为直角三角形.
跟踪训练4.90o
巩固训练
一、选择题1.B 2.D 3.A 4.A 5.B 6.C 7.D
二、填空题8.16 9.0.5<m<1 10.6
11.(-,)解析:易知:OA=OC=,OD=OB=5,CD=AB=,过C作CF⊥x轴,垂足为F,设OF为x,则CF2=CD2-DF2=OC2-OF2,
即:()2-(5+x)2=()2-x2
解得x=,所以CF=,
所以C(-,)
12.40
三、解答题
13.(1)、(2)图略
(3)5
14.解:∵矩形ABCD与矩形AB′C′D′关于点A成中心对称,
∴∠BAD=90 ,AB=AB′,AD=AD′,
∴四边形BDB′D′是平行四边形,DD′⊥BB′,
∴四边形BDB′D′是菱形.
15. 证明:延长BD至E,使DE=CD,连接CE,如图,
∵∠BDC=120°,
∴∠CDE=60°,
∵DE=CD,
∴△CDE为等边三角形,
∴CD=CE=DE,∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,
又∵△ABC是等边三角形,
∴AC=BC,
∴△ACD≌△BCE,
∴AD=BE,
又BE=BD+DE=BD+CD,
∴BD+CD=AD.
16.解:(1)∵四边形ABCD是正方形,
∴AB=BC.
∵AB=BC,BE=BF,
∴AB BF=BC BE,即AF=CE.
(2)AF=CE.理由如下:
∵∠ABC=∠FBE=90°,
∴∠ABF=∠CBE.
∵∠ABF=∠CBE,AB=BC,BF=BE,
∴△ABF≌△CBE,
∴AF=CE.
(3)连接AC,猜想BE=( 1)AB时,AF是EC的垂直平分线.
∵BE=( 1)AB,
∴AE=AB+BE=AB=AC.
∵在Rt△BEF中,BE=BF=( 1)AB,
∴EF=(2 )AB.
∵BC=AB,BF=BE=( 1)AB,
∴CF=BC BF=(2 )AB,
∴EF=CF,
∴AF是EC的垂直平分线.
21世纪教育网(www.21cnjy.com)
《图形的平移与旋转》复习与巩固
【学习目标】
1.了解平移、旋转、中心对称,探索它们的基本性质;
2.能够按要求作出简单平面图形经过平移、旋转后的图形,能作出简单平面图形经过一次或两次图形变换后的图形;
3.利用平移、旋转、中心对称、轴对称及其组合进行图案设计,认识和欣赏轴对称、平移、旋转在现实生活中的应用.
【课前梳理】
1. 平移的概念:在平面内,将一个图形 移动一定的距离,这样的图形运动称为平移,平移不改变图形的 和 .
2.平移的基本性质:一个图形和它经过平移所得的图形中,对应点所连的线段 (或 )且 ;对应线段 (或 )且 ;,对应角 .
3. 点的平移引起坐标的变化规律:沿x轴正方向平移,则 坐标加上平移单位的数量,沿x轴负方向平移,则 坐标减去平移单位的数量;沿y轴正方向平移,则 坐标加上平移的单位数量,沿y轴负方向平移,则 坐标减去平移单位的数量.即:“上加下减,左减右加”
4.旋转概念:在 内,将一个图形绕一个 按某个方向转动一个角度,这样的图形运动称为旋转.这个定点称为 ,转动的角称为 .
5.旋转变换的性质:一个图形和它经过旋转所得的图形中,对应点到旋转中心的距离 ,任意一组对应点与旋转中心的连线所成的角都等于 ;对应线段 ,对应角 .
6.旋转三要素: 、 、 .
7.中心对称概念:把一个图形绕着某一点旋转 ,它能够与另一个图形重合,那么就说这两个图形关于这个点成 ,这个点叫做它们的 .
8.中心对称的性质:成中心对称的两个图形中,对应点所连线段经过 ,且被对称中心 .
9.中心对称图形:把一个图形绕着某点旋转 ,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做 ,这个点叫做它的 .
10.平移、旋转、中心对称三种变换的关系:图形经过平移、旋转或中心对称的变换后,虽然对应位置改变了,但 和 没有改变,即两个图形是全等的.
【课堂练习】
【典型例题1】如图,△ABC的面积为2,将△ABC沿AC方向平移至△DFE,且AC=CD,则四边形AEFB的面积为( ).
A.6 B.8 C.10 D.12
【跟踪训练1】如图,面积为12cm2的△ABC沿BC方向平移至△DEF的位置,平移距离是边BC长的两倍,则图中四边形ACED的面积为( ).
A.24cm2 B.36cm2 C.48cm2 D.无法确定
【典型例题2】如图所示,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AB=1,∠C=30°,则CD的长为( )
A.1 B.1.5 C.2 D.2
【跟踪训练2】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,则∠BAD的度数是( )
A.65° B.70° C.80° D.90°
【跟踪训练3】如图,△ABC中,∠B=70°,则∠BAC=30°,将△ABC绕点C顺时针旋转得△EDC.当点B的对应点D恰好落在AC上时,∠CAE的度数是( )
A.30° B.40° C.50° D.60°
【典型例题3】如图1,O为正方形ABCD的中心,分别延长OA、OD到点F、E,使OF=2OA,OE=2OD,连接EF.将△EOF绕点O逆时针旋转角得到△E1OF1(如图2).
(1)探究AE1与BF1的数量关系,并给予证明;
(2)当=30°时,求证:△AOE1为直角三角形.
【跟踪训练4】在等边三角形ABC中有一点P,已知PC=2, PA=4,PB=,则∠APB= .
【巩固训练】
1.下列运动属于平移的是( )
A.转动的电风扇的叶片
B.打气筒打气时活塞的运动
C.行驶的自行车的后轮
D.在游乐场荡秋千的小朋友
2.把下列数字看成图形,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.在平面直角坐标系中,将点向右平移4个单位长度后得到的点的坐标为
A.(2,3) B.(-6,3) C.(-2,7) D.(-2,-1)
4.如图图形中,把△ABC平移后能得到△DEF的是( )
5.如图,三角形ABC沿着由点B到点E的方向平移到三角形DEF的位置,已知BC=8,EC=5,那么平移的距离为( )
A.13 B.8 C.5 D.3
6.如图,三角形ABC经过平移后得到三角形DEF,下列说法:①AB∥DE;②AD=BE;③∠ACB=∠DFE;④BC=DE.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是AC的中点,将CD绕着点C逆时针旋转一周,在旋转的过程中,点D的对应点为点E,连接AE、BE,则△AEB面积的最小值是( )
A.1 B.2 C.3 D.4
二、填空题
8.如图,将△ABC沿BC方向平移2cm得到△DEF.如果四边形ABFD的周长是20cm,则△ABC周长
是 cm.
9.已知点M(1﹣2m,m﹣1)关于原点的对称点在第一象限,则m的取值范围是 .
10.如图,O是边长为6的等边△ABC三边中垂线的交点,将△ABC绕点O逆时针方向旋转180°,得到△A1B1C1,则图中阴影部分的面积为 .
11.如图,在直角坐标系中,将△AOB绕原点旋转到△OCD,其中A(-3,-1),B(4,3),点D在轴正半轴上,则点C的坐标为 .
12.如图,把△ABC绕点C顺时针旋转得到△A'B'C',此时A′B′⊥AC于D,已知∠A=50°,则∠B′CB的度数是 °.
三、解答题
13.已知,△ABC三个顶点的坐标分别为:A(﹣3,﹣2)、B(﹣5,0)、C(﹣2,2).
(1)在平面直角坐标系中画出△ABC;
(2)将△ABC向右平移5个单位长度,再向上移2个单位长度,画出平移后的△A1B1C1;
(3)计算△A1B1C1的面积.
14.如图,矩形ABCD与矩形A’B’C’D’关于点A 成中心对称,试判定四边形BDB’D’的形状,并说明你的理由
15.已知△ABC是等边三角形,D是∠ABC外-点,且∠BDC=120°,求证:BD+CD=AD.
16.(1)如图①,已知正方形ABCD,点E,F分别在边BC,AB上,且BE=BF.此时AF与CE有怎样的数量关系?
(2)如图②,△BEF绕点B顺时针旋转∠α.当0°<α<90°时,连接AF,CE,此时AF与CE仍有(1)中的数量关系吗?如果成立,请说明理由.否则,请举出反例;
(3)当α=90°时(图③),连接AF,CE.猜想AB与BE有什么数量关系时,直线AF是EC的垂直平行线?试说明理由.
《图形的平移与旋转》章节复习
课堂练习
典型例题1.C 跟踪训练1.36 典型例题2.1 跟踪训练2.D 跟踪训练3.C
典型例题3. (1)AE1=BF1.
证明:∵O为正方形ABCD的中心,∴OA=OD,
∵OF=2OA,OE=2OD,
∴OE=OF,
∵将△EOF绕点O逆时针旋转α角得到△E1OF1
∴OE1=OF1,
∵∠F1OB=∠E1OA,OA=OB,
∴△E1AO≌△F1BO,∴AE1=BF1;
(2)证明:∵取OE1中点G,连接AG,
∵∠AOD=90 ,α=30 ,
∴∠E1OA=90 -α=60 ,
∵OE1=2OA,∴OA=OG,
∴∠E1OA=∠AGO=∠OAG=60 ,
∴AG=GE1,
∴∠GAE1=∠GE1A=30 ,
∴∠E1AO=90 ,
∴△AOE1为直角三角形.
跟踪训练4.90o
巩固训练
一、选择题1.B 2.D 3.A 4.A 5.B 6.C 7.D
二、填空题8.16 9.0.5<m<1 10.6
11.(-,)解析:易知:OA=OC=,OD=OB=5,CD=AB=,过C作CF⊥x轴,垂足为F,设OF为x,则CF2=CD2-DF2=OC2-OF2,
即:()2-(5+x)2=()2-x2
解得x=,所以CF=,
所以C(-,)
12.40
三、解答题
13.(1)、(2)图略
(3)5
14.解:∵矩形ABCD与矩形AB′C′D′关于点A成中心对称,
∴∠BAD=90 ,AB=AB′,AD=AD′,
∴四边形BDB′D′是平行四边形,DD′⊥BB′,
∴四边形BDB′D′是菱形.
15. 证明:延长BD至E,使DE=CD,连接CE,如图,
∵∠BDC=120°,
∴∠CDE=60°,
∵DE=CD,
∴△CDE为等边三角形,
∴CD=CE=DE,∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,
又∵△ABC是等边三角形,
∴AC=BC,
∴△ACD≌△BCE,
∴AD=BE,
又BE=BD+DE=BD+CD,
∴BD+CD=AD.
16.解:(1)∵四边形ABCD是正方形,
∴AB=BC.
∵AB=BC,BE=BF,
∴AB BF=BC BE,即AF=CE.
(2)AF=CE.理由如下:
∵∠ABC=∠FBE=90°,
∴∠ABF=∠CBE.
∵∠ABF=∠CBE,AB=BC,BF=BE,
∴△ABF≌△CBE,
∴AF=CE.
(3)连接AC,猜想BE=( 1)AB时,AF是EC的垂直平分线.
∵BE=( 1)AB,
∴AE=AB+BE=AB=AC.
∵在Rt△BEF中,BE=BF=( 1)AB,
∴EF=(2 )AB.
∵BC=AB,BF=BE=( 1)AB,
∴CF=BC BF=(2 )AB,
∴EF=CF,
∴AF是EC的垂直平分线.
21世纪教育网(www.21cnjy.com)
